深贯穿问题脉冲高度计数减方差技巧

李长楷 汤晓斌 岳爱忠

1（南京航空航天大学 核科学与工程系 南京 210016）

2（中石油测井有限公司 西安 710077）

深贯穿问题脉冲高度计数减方差技巧

李长楷1汤晓斌1岳爱忠2

1（南京航空航天大学 核科学与工程系 南京 210016）

2（中石油测井有限公司 西安 710077）

在处理核测井、辐射防护以及核医学等深贯穿问题时简单使用无偏方法会导致计算时间长且误差大。较新版本的MCNP程序在进行脉冲高度计数时可使用多种减方差技巧。本文使用蒙特卡罗程序代码MCNP5 1.51对包括Mesh-based权窗在内的多种减方差技巧的计算效率进行测试研究，旨在寻求较好的脉冲高度减方差技巧(Pulse height variance reduction techniques, PHVRT)来解决深贯穿问题中计数效率低的问题。计算表明使用DX球配合强迫碰撞生成的权窗可大幅提高计算效率，对各参数进行优化后又可进一步大幅度提高计算效率。最终得出使用Mesh-based权窗配合其他减方差技巧可以很好解决深贯穿问题计算效率低问题。

深贯穿，脉冲高度计数，减方差，Mesh-based权窗

蒙特卡罗方法被公认为处理放射性输运问题最有效的方法[1]，其本质是通过模拟大量粒子输运过程来推断粒子平均输运过程，这使其在计算时很耗费时间[2−6]，MCNP记数结果可以表示为：

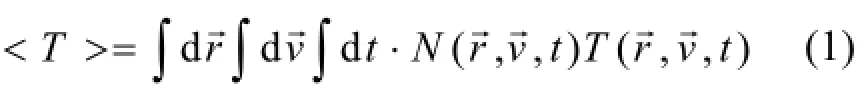
式中，σ是计算值和平均值的偏差；T是计算时间，抽样较好时和抽样粒子数成反比，而T和抽样粒子数成正比，因此对于较好抽样的问题FOM应该趋于稳定。

MCNP脉冲高度计数是粒子输运过程中进入栅元和离开栅元时的能量变化，包括源粒子以及所有次级粒子在栅元的能量沉积，该能量沉积就是粒子输运过程中在栅元的能量脉冲，脉冲高度计数是MCNP唯一需要在粒子输运过程完成才能实现的计数[7−8]。常规的玻尔兹曼通量计数可以在粒子离开栅元或者在栅元里发生碰撞时使用减方差技巧，而在对脉冲高度计数使用减方差技巧时需要额外储存整个粒子输运过程，这使得脉冲高度计数减方差更为复杂[9−12]。

前人已在关于深贯穿问题减方差技巧方面做了大量优秀的工作[13−17]，但很少涉及关于这类问题具体解决办法，以及各脉冲高度减方差技巧(Pulse height variance reduction techniques, PHVRT)实际效果。本文对各减方差技巧的计算效率进行了详细的研究。

1 研究方法

1.1 可用于脉冲高度计数的减方差技巧

1.1.1 源偏倚

源偏倚可以通过降低权重来抽样较多感兴趣的源粒子，包括能量、时间、角度偏倚等。使用该偏倚会按照偏倚的分布进行抽样，而不是按照源的真实分布来抽样，而抽样粒子的权重将被修改为真实分布概率除以偏倚概率分布的值，因此能保证总权重守恒和结果无偏。

1.1.2 几何分裂与轮盘赌

通过给每个栅元赋一个重要性值来控制粒子在栅元间输运的行为，以增加感兴趣栅元的抽样，同时减少不感兴趣栅元的抽样。如前一栅元重要性为i1，第二栅元的重要性为i2，如i2＞i1，则分裂为i2/i1个粒子数，每个粒子权重为Wgt×(i1/i2)，当i2＜i1，则进行轮盘赌，粒子存活的几率为i1/i2，存活粒子权重为Wgt×(i2/i1)，通过设置合适的权重该方法也可增加感兴趣区域的抽样。

1.1.3 暗含俘获

暗含俘获也称为存活偏倚，即碰撞不吸收（杀死）粒子而是降低其权重，如碰撞总截面为X，吸收截面为X1，则碰撞后粒子权重降为Wgt(1−X1/X)，而不是按X1/X的概率被吸收，从而保证了较多的有效抽样粒子，但这样做的缺点是保留了大量权重极低的粒子，因此该方法必须与权重截断或权窗一起使用来控制低权重粒子的数量。

1.1.4 指数变换

通过修改粒子在物质中的微观截面来改变指向特定方向的自由程，同时粒子权重也会被相应修改。

式中，φ*是修改后的总截面；φ是修改前的总截面；μ是粒子方向和拉伸方向夹角的余弦。P＞0时，会使其在物质中的穿透性增强，该方法与强迫碰撞不可发生在同一栅元里，本文下面所用指数变换和强迫碰撞结合使用是指二者在不同栅元里使用。

1.1.5 强迫碰撞

强迫碰撞与暗含俘获相似，将进入栅元的粒子分为碰撞和不碰撞两类，并由不碰撞的粒子携带剩下的权重离开栅元。该方法不仅适用于增加光疏介质栅元碰撞，也同时适用于增加光密介质的通过性。由于在使用强迫碰撞时权重截断是关闭的，因此在相邻几个栅元同时使用强迫碰撞会导致大量低权重粒子产生并极大增加计算时间。

1.1.6 DX球(DXTRAN)

DX球一般用于不能很好抽样的小区域，通过设置DX球，在球外每次碰撞中都会产生一个DXTRAN粒子(DXTRAN particle)，该粒子按确定几率散射到DX球表面，期间不再参与碰撞，权重按确定性输运计算。由于强迫碰撞会增加球外碰撞次数，DX球粒子数也会相应增加，因此在DX球外栅元使用强迫碰撞可以增强DX球效果。

1.1.7 权窗

权窗原理是在源与计数区之间设立一系列权重区间，权重窗上限值取下限值的固定倍数，粒子权重高于能窗上限时会分裂，低于能窗下限时粒子会进行轮盘赌。该方法与几何分裂相似，权窗与几何分裂的区别在于几何分裂不考虑权重值的大小只考虑相邻栅元间的重要性比值，而权窗中需要将粒子的权重值与权窗上、下限进行比较来控制其分裂和轮盘赌，其特有的抑制过度偏倚功能使其和其他减方差技巧有很好的兼容性。可以将权窗形象比喻为“由源通向计数区域的走廊”。

MCNP提供的权窗生成器能自动计算权窗重要性函数，通过模拟一定数量的粒子，重要性的计算可表示为：重要性=（进入该栅元粒子对计数的贡献/进入栅元的总权重），然后按重要性倒数的分布指定权窗下限值。权窗的生成过程也涉及到粒子统计过程，通过使用偏倚技巧可较快生成有效的权窗。权窗生成器有效避免了人为因素，且其生成的权窗效果往往好于人为设定的重要性值。

1.2 计算模型和计算方法

本文计算模型是γ密度测井(图1)。直径10 cm的钨镍合金测井工具放置于直径20 cm的井眼内，井内充满水，各向同性的137Cs点源位于一个45°斜向上的准直装置中，远探测器为ø50×48 mm NaI(TI)探测器，位于距源40 cm处，晶体表面镀0.03 cm的镉膜。由于钨镍合金对γ射线屏蔽系数很高，对探测器计数贡献最大的是经斜准值孔射入地层的粒子，这部分粒子占总粒子份额很少，这会引起计数区域抽样不足，该问题属于深贯穿问题，有必要使用减方差技巧。

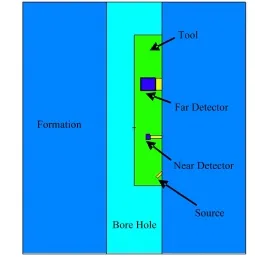
图1 γ密度测井的蒙特卡罗模型Fig.1 Monte Carlo model of gamma-ray density well.

由于减方差技巧的偏倚性，不能同时使远近探测器获得较好的抽样，本文只对远探测器计数进行讨论。本文各减方差技巧的参数选择均是使用MCNP_pstudy功能，在参数可选区间做均匀线性插值分别计算并对比结果得到的最优值，MCNP插值命令是c @@@ p=uniform 10 min max。对0−0.665MeV能量区间设100个能量箱，对探测器进行脉冲高度计数并对计数结果进行高斯展宽。由于脉冲高度计数不可以和权窗生成器WWG同时使用，本文使用F4（径迹长度计数）生成权窗，并将该权窗用于脉冲高度计数。

图2为加Mesh权窗效果图，本文选用直角坐标Mesh，虚拟网格数量为20×20×30，采用均匀分布。

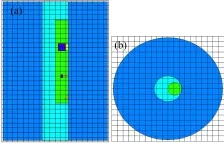
图2 权窗虚拟网格轴向和径向分布(a) xz方向，(b) xy方向Fig.2 Radial and axial cross-section views of weight windowvirtual grid distribution.(a) Axial cross-section views, (b) Radial cross-section views

2 计算结果与分析

2.1 不使用任何减方差技巧

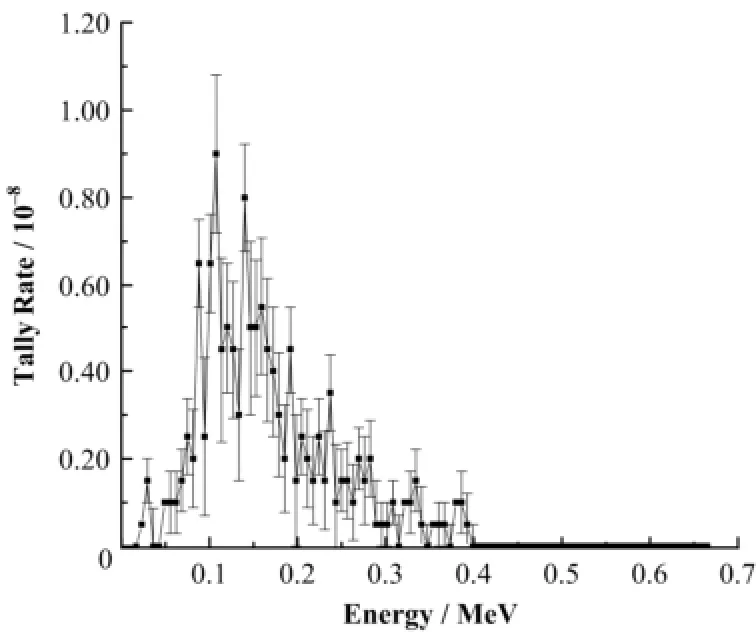
图3 不使用减方差技巧的探测器响应曲线Fig.3 Corresponding curve got with no variance reduction techniques.

由图3可见，计算结果各能量箱误差太大，导致计算结果不可信。

2.2 使用常规减方差技巧

运行2×109粒子周期各减方差技巧的计算效率值如表1所示。本文的相对误差是指总计数的相对误差。

不使用任何减方差技巧运行2×109个粒子周期，相应探测器响应曲线如图3所示。

表1 单个减方差技巧计算效率Table 1 Computational efficiency with one PHVRT.

由表1，使用DX球计算效率最高，因为该方差技巧可以极大程度提高指定区域的抽样，指数变换、源偏倚和几何分裂也可以通过提高在指定方向的抽样从而较大幅度提高计数效率，暗含俘获由于其全局性特点，在提高对计数贡献大的区域粒子生存几率的同时也提高了其他区域的粒子生存几率，单独使用时其对计数效率影响不大。强迫碰撞也可以提高粒子生存几率但其可以发生在指定区域，因此在对计数贡献大的区域使用强迫碰撞可以提高计数效率。

将DX球和其他减方差技巧结合使用运行2×109粒子周期，计算效率如表2所示。

表2 DX球与其他减方差技巧结合计算效率Table 2 Computational efficiency of DXTRAN used in conjunction with the other variance reduction techniques.

由表2可见，DX球和其他所有减方差技巧结合使用都会较大幅度提高其计算效率，其中DX球和源偏倚同时使用有较高的计算效率，因为该问题中几乎只有通过准直孔进入地层的粒子才可能对计数区有贡献，其对应响应曲线如图4所示。

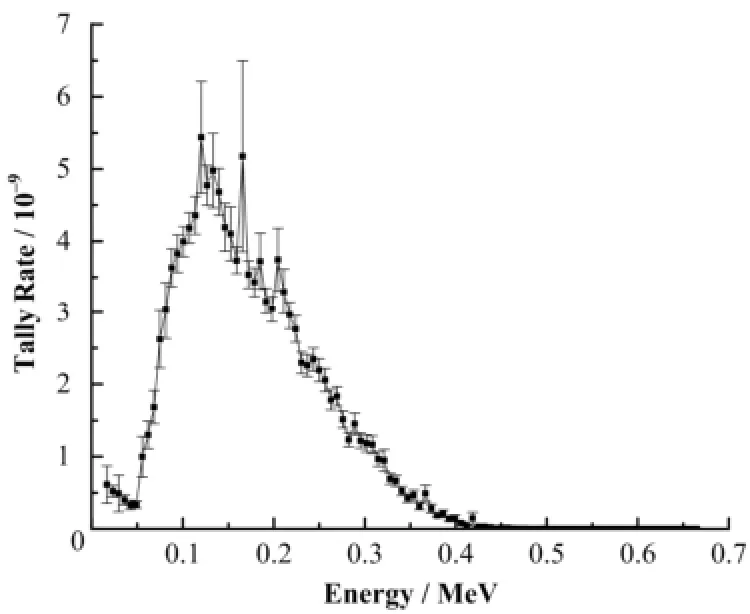
图4 DX球和源偏倚配合使用计算结果Fig.4 Corresponding response curve achieved by using DXTRAN with source bias.

图4 中其各能量箱计算误差约为20%，一些区间误差甚至更大，结果依然不可信。可见常规减方差技巧不能很好地解决深贯穿问题。下面的计算会采用一种自动减方差技巧-权窗减方差。

2.3 使用Mesh权窗

权窗值只与计数相关而和栅元密度无关，为较快生成有效权窗本文对主要材料做降低密度处理，将地层和钨镍合金的密度分别降为实际值的1/10。为验证这样做的可行性，分别用降低后的密度和实际密度条件下生成的权窗用于实际密度的计算，并对计算结果进行对比。如图5所示，两条响应曲线吻合度很高，其中两条曲线各能量箱误差都在0.5%以下，可见密度对权窗有效性没有影响。

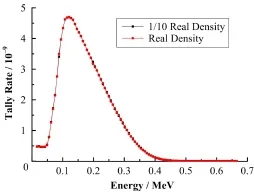
图5 减密度和真实密度所得权窗结果对比Fig.5 Corresponding response curve achieved by using weight window generated by reduced density and real density respectively.

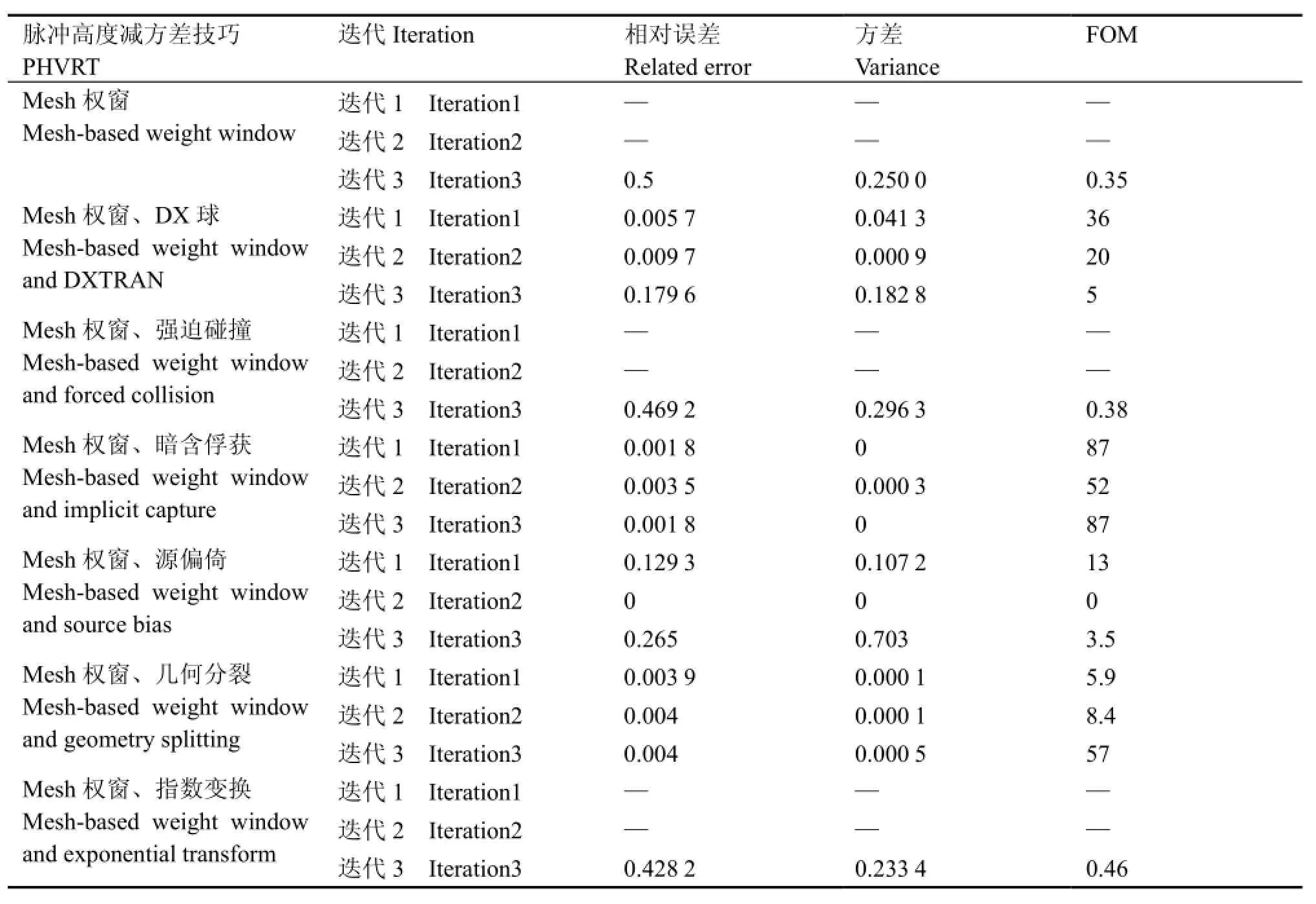
表3 Mesh权窗与其他一种减方差技巧结合使用计算效率Table 3 Computational efficiency achieved by using mesh-based weight window in conjunction with one of the other PHVRT.

使用Mesh-based权窗，并使用一种其他减方差技巧，在1/10主要物质密度条件下运行2×107粒子周期生成权窗，将该权窗用于接下来的真实密度条件计算，相应权窗计算效率值见表3。

其中迭代1表示使用降低密度条件下生成的权窗进行实际密度计算，计算中使用相应的减方差技巧；迭代2表示使用降低密度条件下生成的权窗进行实际密度计算，计算中不使用任何其他减方差技巧；迭代3表示使用迭代1过程中生成的权窗进行实际密度计算，计算中和权窗生成时使用了同样的减方差技巧；—表示无法得到有效计算结果。

由表3可见，权窗和暗含俘获有较好的相容性，暗含俘获保证抽样粒子有较大数量，其和权窗配合使用可以去除大量对计数贡献小的低权重粒子，而使计算时间不致太长。定向计数功能的DX球生成的Mesh-based权窗也有较好的效果。

DX球结合其他减方差技巧一起使用生成权窗，只使用除DX球外的一种减方差技巧。

由表4，通过使用强迫碰撞配合DX球可以在迭代3中大幅提高Mesh权窗的计算效率，其原因是强迫碰撞可以增加对计数区有贡献栅元的粒子存活几率，也就增加了在该区域碰撞产生DXTRAN粒子的数量，并通过权窗去除大量低权重粒子，从而有较大的计算效率。表5为加一种其他减方差技巧和二者配合使用的计算效率。

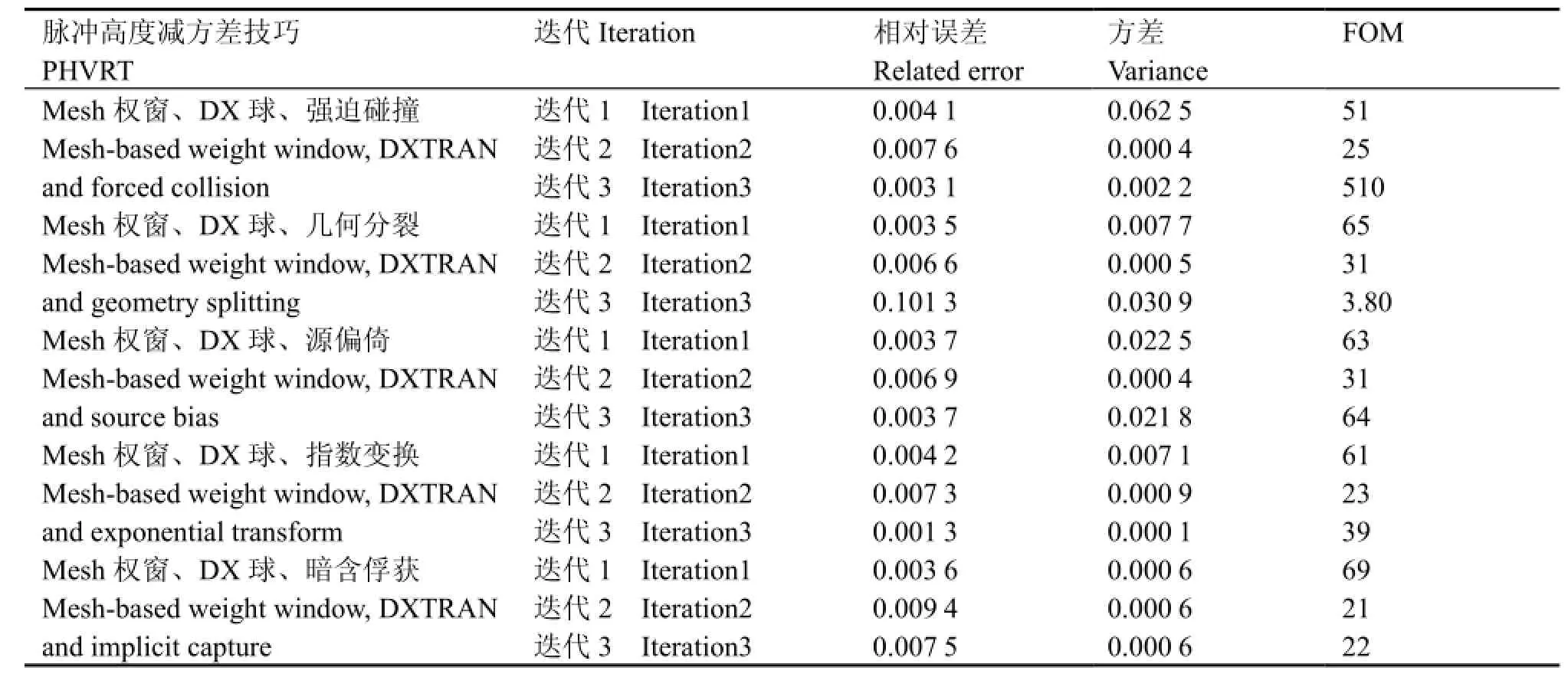
表4 Mesh权窗和DX球与其他减方差技巧结合计算效率Table 4 Computational efficiency of Mesh-based weight window and DXTRAN in conjunction with one of the other PHVRT.

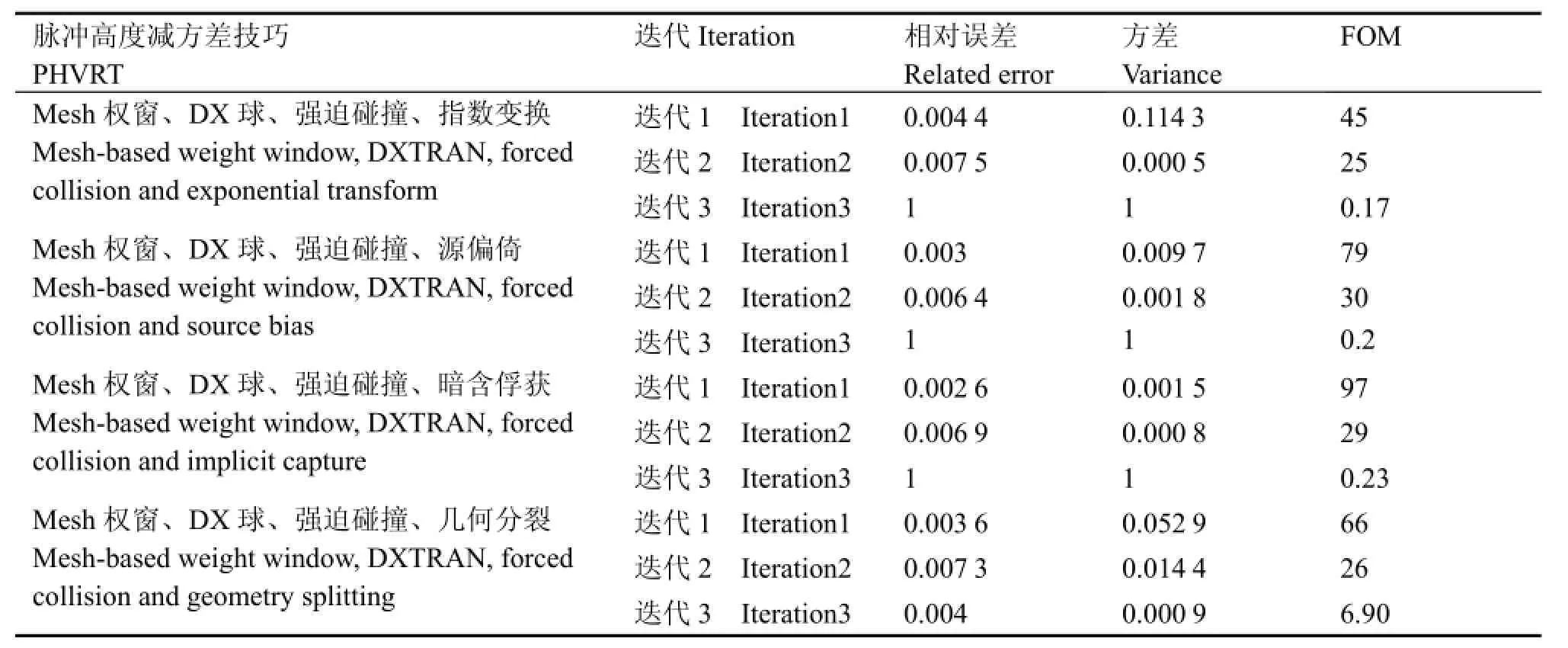
表5 Mesh权窗和强迫碰撞以及DX球与其他减方差技巧结合使用计算效率Table 5 Computational efficiency of Mesh-based weight window, DXTRAN and forced collision in conjunction with one of the other PHVRT.

生成权窗过程中再加上其他减方差技巧反而会降低所生成权窗的计算效率。其原因是多种减方差计数互相干扰使生成权窗下限过低导致大量极低权重粒子产生而影响计算速度；生成权窗上限过高使大量粒子因轮盘赌而损失，导致抽样不足。

目前为止，使用DX球和强迫碰撞配合权窗在迭代1中生成的权窗是最好的，为进一步提高计算效率，接下来使用该权窗配合DX球以及强迫碰撞计算时加入其他减方差技巧，各减方差组合计算效率如表6所示。

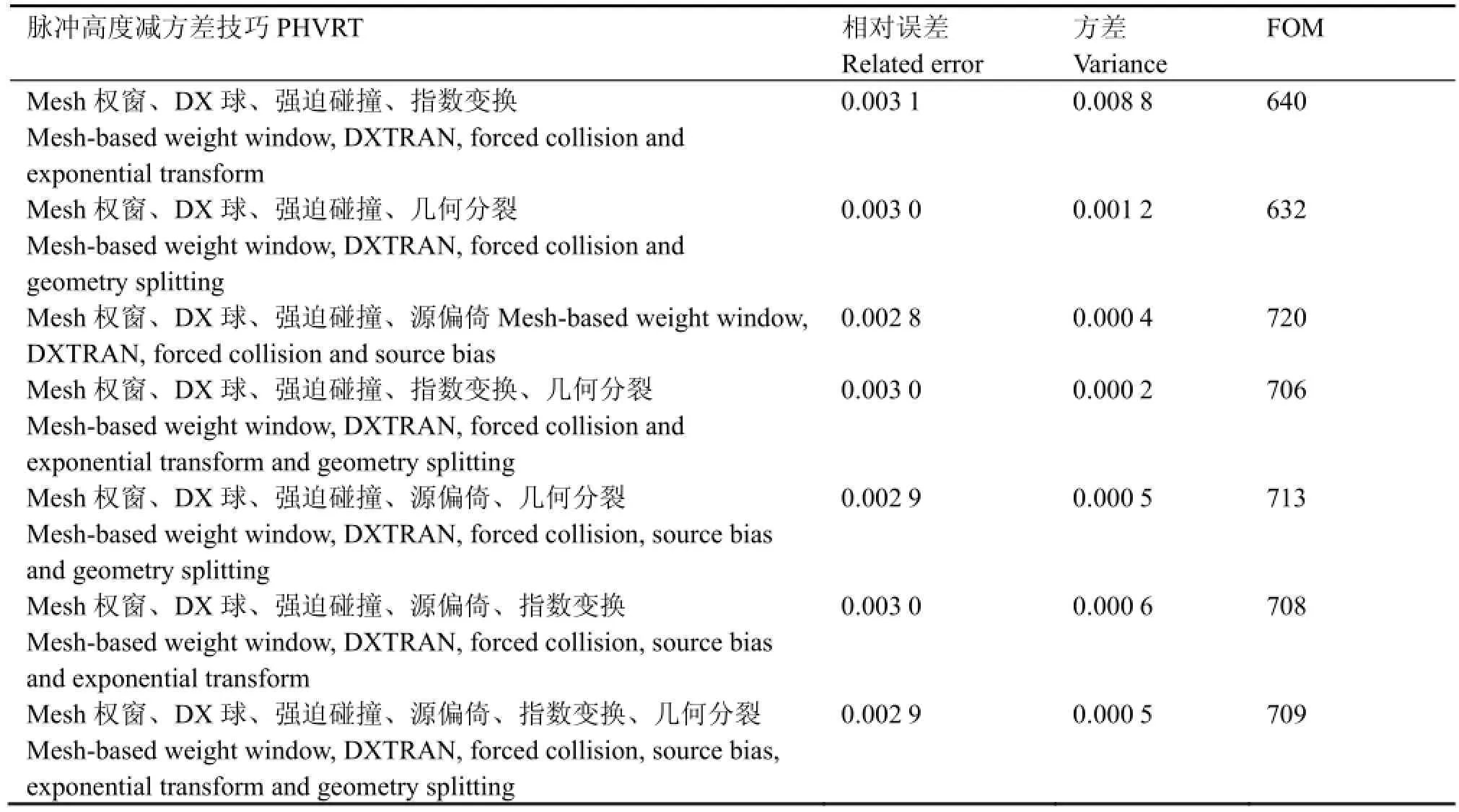
表6 Mesh权窗和强迫碰撞生成的权窗配合其他减方差技巧一起使用计算效率Table 6 Computational efficiency of improved PHVRT.

如表6所示，加上其他减方差技巧后各组合均较原来有较大提高，说明权窗和其他减方差技巧有很好的兼容性。

为显示本文减方差技巧的效果，对比没使用减方差技巧的二维可视化输运过程和使用本文减方差技巧的二维可视化输运过程。

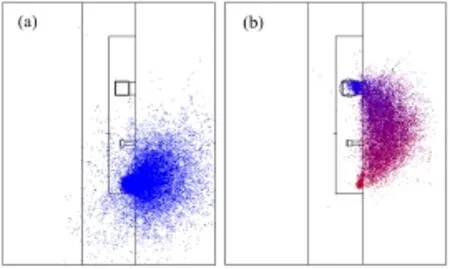
图6 可视化运行粒子碰撞轨迹，虚线是DX球(a) 不使用减方差技巧运行50 000个粒子周期，(b) 使用减方差技巧运行500个粒子周期Fig.6 Particle collisions in the visualization tool, the dotted box is DXTRAN.(a) Collisions of 50 000 particles histories with no PHVRT, (b) Collisions of 500 particles histories with PHVRT

图6 (a)中整个输运过程粒子权重不变，计数区不能得到很好的抽样。图6(b)粒子权重由下到上依次递减，计数区抽样粒子权重较低但可以得到很好的抽样。

3 结语

本文列出多种可用于脉冲高度计数的减方差技巧并作简要介绍说明，通过对比深贯穿问题中脉冲高度计数多种减方差技巧的计算效率，得出

Mesh-based权窗与其他减方差技巧结合使用解决这类问题有很好的效果；提出使用常规的玻尔兹曼计数产生的权窗用于脉冲高度技术以克服脉冲高度计数不能和权窗生成器结合使用的不足；提出权窗值和密度无关，通过降低密度可以较快生成有效权窗。

本文所有减方差技巧均适用于脉冲高度计数以外的常规玻尔兹曼计数。

1 Brown F B, Sweezy J E, Bull J S, et al. Verification of MCNP5[R]. Version 1.50, LA-UR-08-3443, USA: Los Alamos National Laboratory, 2008

2 Wagner J C, Peplow D E, Evans T M. Automated variance reduction applied to nuclear well-logging problems[J]. Nuclear Technology, 2009, 168(3): 799−809

3 Wagner J C. An automated deterministic variance reduction generator for Monte Carlo shielding applications[C]. Proceedings of the American Nuclear Society 12thBiennial RPSD Topical Meeting, 2002: 14−18

4 Junli L, Zhi Z, Rui Q, et al. An auto-importance sampling method for deep penetration problems[J]. Progress in Nuclear Science and Technology, 2011, 2: 732–737

5 Booth T E. Sample problem for variance reduction in MCNP[R]. Los Alamos National Laboratory, USA: NM, 1985

6 Cramer S N. Variance reduction methods applied to deep-penetration problems[R]. Oak Ridge National Laboratory, USA: TN, 1984

7 Hughes H G. Variance reduction with pulse-height tallies in MCNP[R]. Rapport Technique LA-UR-07-6660, USA: Los Alamos National Laboratory, 2007

8 Booth T E. Pulse-height tally variance reduction in MCNP[R]. Los Alamos Report LA-13955, USA: Los Alamos National Laboratory, 2002

9 Sood A, Forster R A, Adams B J, et al. Verification of the pulse height tally in MCNP 5[J]. Nuclear Instruments and Methods in Physics Research Section B: Beam Interactions with Materials and Atoms, 2004, 213: 167−171

10 Bull J S, Booth T E, Sood A. Implementation of pulse height tally variance reduction in MCNP5[R]. Technical Report LA-UR-08-2330, USA: Los Alamos National Laboratory, 2008

11 Booth T E. Monte Carlo variance reduction approaches for non-Boltzmann tallies[R]. Los Alamos National Laboratory, USA: NM, Funding Organization: USDOE, Washington DC, 1992

12 Olsher R H. A practical look at Monte Carlo variance reduction methods in radiation shielding[J]. Nuclear Engineering and Technology, 2006, 38: 225−230

13 Haghighat A, Wagner J C. Monte Carlo variance reduction with deterministic importance functions[J]. Progress in Nuclear Energy, 2003, 42(1): 25−53

14 Smith H P, Wagner J C. A case study in manual and automated Monte Carlo variance reduction with a deep penetration reactor shielding problem[J]. Nuclear Science and Engineering, 2005, 149(1): 23−37

15 Hendricks J S, McKinney G W. Pulse-height tallies with variance reduction[C]. Proceedings of the ANS Monte Carlo 2005 Topical Meeting, 2005: 17−21

16 van Riper K A, Urbatsch T J, Soran P D. AVATAR-automatic variance reduction in Monte Carlo calculations[R]. Los Alamos National Laboratory, USA: NM, 1997

17 Wagner J C, Haghighat A. Automated variance reduction of Monte Carlo shielding calculations using the discrete ordinates adjoint function[J]. Nuclear Science and Engineering, 1998, 128(2): 186−208

CLC TL99

Pulse-height tally variance reduction in deep penetration problem

LI Changkai1TANG Xiaobin1YUE Aizhong2

1(Department of Nuclear Science and Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China)
2(China Petroleum Logging Co., Ltd, Xi'an 710077, China)

Background: In deep penetration application such as well-logging, medical physics and radiation shielding, analog Monte Carlo method will cause long calculation time and large variance. The newly released Monte Carlo code MCNP5 version 1.51 allows almost all of MCNP's variance reduction techniques to be used with pulse height tally. Purpose: This paper aims to find an optimize pulse height variance reduction technique (PHVRT) to solve low efficiency with pulse-height tallies in deep penetration problems. Methods: A variety of variance reduction techniques including an auto-important sampling method-Mesh-based weight windows were proposed, and all kinds of variance reduction techniques proposed were tested and results with different variance reduction techniques were compared. Results: Mesh-based weight windows used with DXTRAN and forced collision get good calculation efficiency. After optimizing, the efficiency can be improved with large amplitude. Conclusion: Mesh-based weight window used with other variance reduction techniques can resolve deep penetration problem effectively.

Deep penetration, Pulse height tally, Variance reduction, Mesh-based weight windows

TL99

10.11889/j.0253-3219.2015.hjs.38.030501

No.11475087)资助

李长楷，男，1987年出生，2014年于南京航空航天大学获硕士学位，从事核测井研究

2014-11-04，

2014-12-12