康普顿相机的GEANT4模拟与反投影图像重建

丁长骥 毛本将 袁永刚 姜志刚 杨朝文

1（四川大学 物理科学与技术学院 辐射物理及技术教育部重点实验室 成都 610065）2（中国工程物理研究院 核物理与化学研究所 绵阳 621900）

康普顿相机的GEANT4模拟与反投影图像重建

丁长骥1,2毛本将2袁永刚2姜志刚2杨朝文1

1（四川大学 物理科学与技术学院 辐射物理及技术教育部重点实验室 成都 610065）
2（中国工程物理研究院 核物理与化学研究所 绵阳 621900）

模拟构建了双层康普顿相机，利用康普顿散射原理，获取γ光子在两层探测器发生散射前后沉积的能量和位置信息，通过一定算法进行图像重建，获得放射源位置信息。该相机具有灵敏度高、体积小、应用范围广等优点。通过蒙特卡罗方法模拟了具有双层条状结构位置灵敏探测器（散射探测器、吸收探测器）组成的康普顿相机，其两层探测器分别由Si和Ge材料构成。利用反投影图像重建算法实现了放射源图像重建，当单点源与探测器距离为40 mm时，成像的效率为0.38%，位置分辨率达到8.0 mm，角分辨率达到3°。对于不同位置和不同个数点源的情况下，检验了反投影重建算法在康普顿相机放射源空间重建中的效果。

康普顿相机，蒙特卡罗模拟，反投影图像重建算法

20世纪70年代，Todd[1]首次提出了康普顿相机的概念，但由于当时探测器材料和电子学数据采集技术的限制，该技术未得到深度发展。而同时期能对放射性物质进行二维定位的单孔和编码孔成像技术却得到了较好发展。但相比之下，其成像效率和探测面积都不如康普顿相机，且体积更大，重量也更重。在放射性核素应用越来越广泛的今天，出于各种应用和安全的考虑，对于放射源的检测更为重要，需要精确的探知放射源所在具体地点，从而可有针对性地处理。

γ相机在天体物理、核设施退役、特殊核材料结构分析、放射性核素示踪等各种重要领域都有重要应用。所以作为指标优良的康普顿相机应用前景也是十分广泛。在核材料检测方面，康普顿相机有十分重要的应用。

2007年，利弗莫尔实验室成功地开发出一款康普顿相机SPEIR (SPEctroscopic Imager for γ-Rays)，该相机采用两块阵列（直径70 mm）式Ge探测材料，每块Ge材料的尺寸为2 cm×2 cm×2cm；探测成像的能量为150 keV−4 MeV，由于SPEIR系统采用Ge探测器，采用制冷的方式，系统成本较高[2]。之后也有许多由不同探测器、探测材料组成的康普顿相机问世。目前国内对其研究较少，未制作实际应用的康普顿相机，也并没有系统地对其进行模拟研究。本文通过对其蒙特卡罗模拟获得了理论数据，重建算法的构建为实现算法优化提供了支撑。

1 康普顿相机

康普顿散射中散射光子能量由式(1)决定：

式中，Ec为散射光子能量；E0为初始光子能量；θ为散射角；mec2为电子的静止能量。

若其初始入射的光子为单能的话，当散射角唯一时，则散射光子的能量也唯一确定。反之若已知初始能量E0与散射光子能量Ec，则散射角θ也是唯一确定的，康普顿相机正是利用此原理对放射源进行定位。在具体重建算法中会考虑散射材料对光子的多普勒效应。

基本的康普顿相机由两层探测器组成，如图1所示。第一层探测器称为散射探测器(Scattering detector)，均匀分割成多个单元，构成位置和能量皆灵敏的探测器阵列。来自样品的γ射线在第一个探测器中发生康普顿散射，在其中沉积能量为E1，散射位置为x1。第二层探测器称为吸收探测器(Absorbing detector)，康普顿散射产生的散射光子被吸收探测器完全吸收，沉积能量E2，吸收位置为x2。γ在两个探测器中的相互作用位置x1、x2和能量沉积E1、E2均可直接由两个位置灵敏探测器测量，γ射线的能量E0可由E1加E2得到。两层探测器多采用Si、Ge半导体探测器，以此获得高的能量分辨率与精确的位置信息。

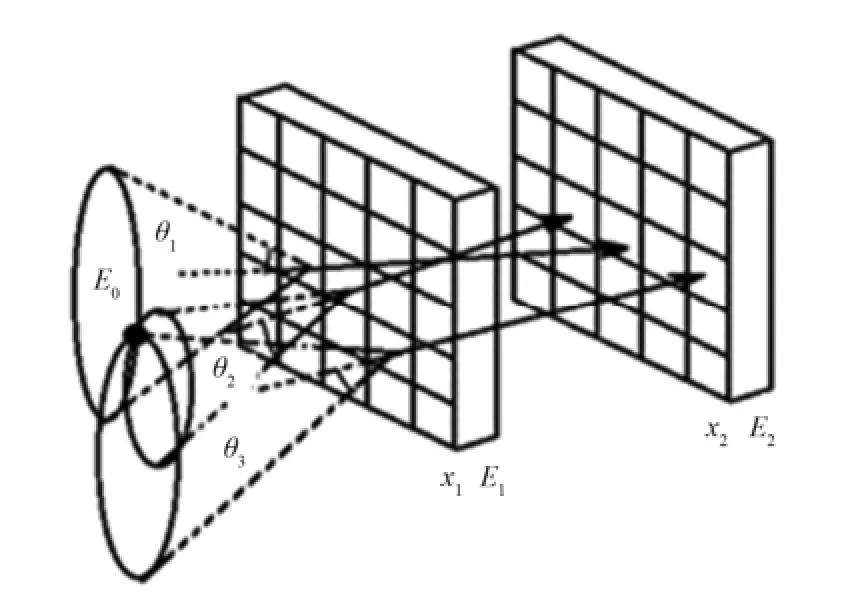
图1 康普顿相机原理示意图Fig.1 Schematic representation of Compton camera.

由于康普顿散射公式没有给出任何方位角φ的信息，所以γ射线的发射位置一定处于一个圆椎表面上的某一点，这个圆椎的顶点为x1、中轴线为x1x2、半角为θ。经过多次符合条件的事件，可以得到很多圆锥，理论上放射源所在位置就是这些圆锥所交汇的部分。图像重建时在成像空间内，每个像素或体素通过一定的算法得到其权重，经过阈值筛选，确定放射源位置。

根据康普顿相机的原理，探测部分有散射探测器与吸收探测器两部分，且同时对位置和能量灵敏。散射探测器记录γ光子在散射探测器中发生康普顿效应所沉积的能量与发生散射的位置；吸收探测器记录发生康普顿效应之后产生的散射光子在吸收探测器中能量沉积与发生能量沉积的位置，在探测器中沉积的能量即是γ光子转移给电子的能量。所以理想的探测器为阵列式，可方便清晰地记录和得到每次反应所在位置与在此位置上所产生的能量沉积。

当阵列式康普顿相机所包含探测单元较多时，所需电子学线路也较多，因此对符合电路与其他电子学系统等要求很高。因此基本的康普顿相机散射、吸收探测器由双层正交放置的位置灵敏条状半导体探测单元构成，如图2所示。

一方面双层条状探测单元可以对γ光子反应处的横纵坐标同时输出，获得作用位置与其所沉积的能量。另一方面，将普通的阵列式输出变为由条状探测器分别输出，简化了电子学线路。

图2 典型的康普顿相机结构[3]Fig.2 Typical structure of Compton camera[3].

2 康普顿相机GEANT4模拟

在康普顿相机的研究过程中，使用GEANT4的标准模型作为工具进行计算机模拟，不仅可以模拟构建出相机模型，获得放射源图像重建所需数据，构建和验证重建算法，而且能够获得探测器设计理论依据和数据来源，同时验证相机性能，对探测器的设计提出改进。

康普顿相机中对能量和位置同时灵敏的探测单元尺寸应当较小，如果探测器尺寸过大，会导致输出电路路数过多，且需要对大量事件进行一个符合甄别，在电子学实现上有难度；同时如果两个探测器间距过大，会导致从散射探测器出来的散射光子进入吸收探测器的几率变小，使康普顿相机效率降低。经过多次初步模拟，确定康普顿相机结构如图3所示，散射探测器、吸收探测器均由双层条状探测单元构成。模拟的γ光子能量为137Cs源0.662MeV。

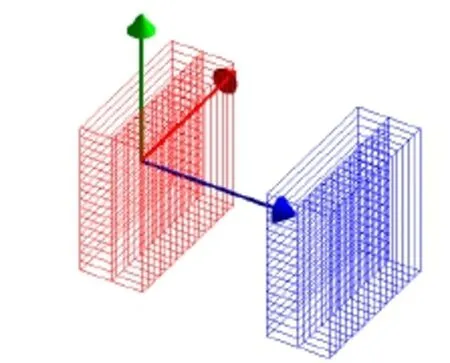
图3 康普顿相机模拟效果图Fig.3 Compton camera simulation representation.

左侧部分为散射探测器，由Si材料组成。获得的沉积能量分辨率高，散射处位置分辨率好，同时对于0.662 MeV能量的γ光子散射效果较好。经过多次初步模拟确定每个条状单元尺寸为48 mm× 10mm×3 mm，第一层16个探测单元平行于x轴方

向放置；第二层16个探测单元平行于y轴方向放置，使得两层探测单元正交。散射探测器整体尺寸为48mm×20 mm×48 mm。右侧的吸收探测器由双层条状Ge材料组成，对γ光子沉积能量与作用位置探测灵敏，其探测单元结构、放置与尺寸都与散射探测器相同。散射探测器与吸收探测器相距40 mm。

一个值得注意的问题是从放射源发出的大量γ光子，每个γ光子从产生到消失（能量在探测器中沉积完全或者逃逸出模拟空间）称为一个事件。根据康普顿相机原理，符合条件的事件应当满足：一个γ光子从放射源发出后，在散射探测器第一层发生一次康普顿散射，在第一层中产生次级电子，次级电子在第二层对应单元产生信号，通过两层分别产生信号的探测单元得到γ光子散射位置。之后的散射γ光子在吸收探测器中沉积完所有能量，意味着在吸收探测器中发生的过程可以是一次光电效应，也可以是经过康普顿效应后再发生光电效应等。总之，需要把散射γ光子所有的能量都沉积消耗在吸收探测器中。但在蒙特卡罗模拟中，大部分γ光子所经历的过程产生的事件，并不是我们所需要的。例如一个γ光子直接在散射探测器中发生光电效应；或者在散射探测器中发生一次康普顿效应后，产生的散射γ光子没有进入吸收探测器，或者进入吸收探测器但并没有将能量完全地沉积消耗。为此，模拟得到的大量事件需要经过一定的筛选，得到符合要求的事件进行重建。

模拟过程中的甄别根据能量来进行：第一层探测器只发生一次康普顿散射并且γ光子在两层探测器将能量都沉积完全。在实际探测器中，时间甄别与能量甄别都是需要的。时间甄别判断不同能量沉积是否属于同一个γ光子，然后再进行能量甄别，判断是否满足能量沉积完全这个条件。如果存在能谱展宽时，γ光子的能量甄别就变为一个范围，当一个γ光子所有的沉积能量在此范围内，那么就判断其符合能量甄别条件。

3 反投影图像重建算法

根据康普顿相机对放射源探测的原理，需要采用适合康普顿相机的重建算法对获得的数据进行计算，从而得到放射源所在位置空间信息。在反投影图像重建算法中（后文简称反投影法），针对康普顿相机，我们可以把放射源所在的空间区域即成像空间分隔为立方体网格状空间，每个立方体空间都作为一个体素。很明显，在成像空间范围一定的时候，分隔成的体素数量决定着体素的大小，体素的大小影响着对放射源重建之后的位置分辨率。

康普顿相机中，放射源所产生的γ射线距离散射探测器的轨迹为一条直线，但根据其探测原理，实际所确定出来的只有以直线轨迹为中心轴的圆锥面而已，即放射源在这样的一个圆锥面上，而无法确定其精确位置。在康普顿相机的反投影法中，利用大量事件所产生的圆锥面的交集的位置，就是放射源所在位置概率最大的地方。

反投影示意图见图4。反投影法简单地通过基于体素的权重进行投影从而重建图像，各个体素在每次事件产生的圆锥经过计算都可以获得一定权重。权重作为对应于特定的体素和圆锥的事件的一个近似估算的概率。其中每一个事件都可以获得这次事件中每个体素的一个权重，然后统计所有事件得到每个体素所估计的强度，来确定分布在成像空间的γ射线发射核素的位置。放射源在每个体素的概率即是与这个体素所有事件权重的总和成正比。

图4 反投影示意图Fig.4 Backprojection diagram.

估计的权重计算通过整合概率密度函数在事件体素圆锥表面计算得到。

式中，ωij是在投影事件中，事件j在体素i所对应的估计权重；r代表成像空间中某一点的位置坐标。权重的计算可以由pdf (probability density function)函数计算各个体素得到。

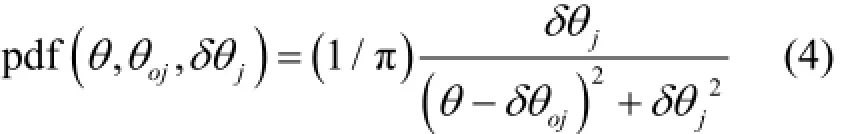
式中，θoj为jth圆锥的孔径大小；θ−θoj是从对应视野的点到jth圆锥面的最小角距离；δθj是圆锥孔径的角误差。由于实际散射角与计算得到的圆锥角误差不会完全相同，所以权重的具体计算公式在不同范围内有所不同[4]。

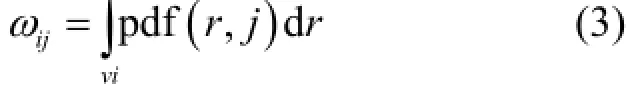
4 反投影法图像重建

4.1 单点源条件

散射探测器靠近放射源的一面为XY平面，探测器表面中心点垂直向外为Z轴。在GEANT4中构造一个点源，发射角度一定，坐标(0,0,40)，位于Z轴上，与散射探测器表面距离为40 mm。散射探测器外侧定义为一立方体成像空间，成像网格空间体积为60 mm×60 mm×60 mm，一共分割为121×121× 61个体素，每个体素在XY平面间隔0.5 mm。因此，成像空间在Z轴的范围是10−70，每层切面相距1mm。

计算得到大量模拟数据，经过筛选保留符合康普顿相机成像条件的事件。利用反投影法计算得到平行于XY平面不同距离处，即不同Z轴坐标处切面的体素的权重，获得放射源重建图像，其中考虑了Si材料对散射光子的多普勒效应。距离散射探测器由远及近切面的成像效果如图5所示。

图5 (a)−(i)依次表示沿Z轴坐标由大变小，即成像切面与散射探测器距离由远及近时各切面的成像效果。根据康普顿相机成像的原理，平行于XY平面的切面与每次事件所形成的圆锥面相交形成一个椭圆，大量事件产生大量椭圆，而椭圆相交处即是放射源所在位置概率最大处。图5中，随着成像空间的切面Z轴坐标由大变小，切面向探测器靠近，在图5(g)中Z=17处达到最高分辨率，之后随着距离越靠近得到的分辨率也在下降。图5(g)的XZ面权重峰形如图6所示。

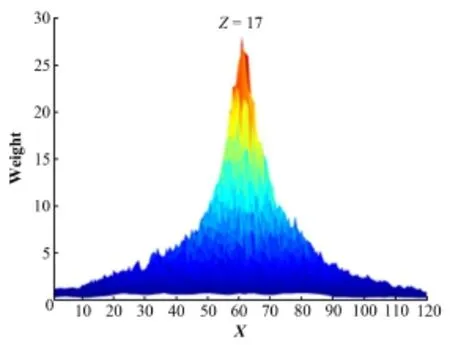
图6 单源图5(g)的XZ面峰形Fig.6 XZ-palne peak shape of single source in Fig.5(g).

图7 单源图5(g)的XZ面峰形权重Fig.7 XZ-palne peak weight of single source in Fig.5(g).

将一维位置谱的半高宽(Full Width at Half Maximum, FWHM)定义为康普顿成像装置的空间分辨率，图7中可以得到在此条件下位置分辨率FWHM=8.0 mm，点源产生的γ光子为200000，筛选符合的个数为760，定义其成像效率为0.38%，角分辨率为3°，优于通常采用的机械准直器的成像系统空间位置的分辨率和成像效率。随着放射源离探测器距离的增大，空间位置分辨率和效率都会明显降低[5]。

4.2 双点源条件

当模拟放射源为双点源时，探测器距离、探测器、成像的条件和算法都不发生改变。两点源位于平行于XY平面的同一平面上，坐标为(10,10,40)、(−10, −10,40)。两个点源发射γ光子的概率，发射角度完全相同。与单源相同，图8(a)−(i)依次表示沿Z轴坐标由大变小时各切面的成像效果，如图8所示。

图8 双点源不同距离处切面的成像Fig.8 Imaging of facet with different distance by double point.

图8 中显示了双点源情况下由远及近不同切面处的重建图像，在图8(g)中可以得到清晰的双点源重建图像。图9代表双点源其中一个点源的峰形，可以得到点源空间分辨率为FWHM=10.0 mm， 200000个γ光子中符合要求的个数为713，成像效率为0.36%。与单源相比，其空间分辨率、角分辨率与成像效率都有所降低，原因是双源所产生的γ光子相互干扰，降低了成像的质量。

图9 双源图8(g)中左侧点源XZ面峰形权重Fig.9 XZ-palne peak weight of left single one of double source in Fig.8(g).

随放射源数目增加，虽然分辨率下降明显，但当在反投影重建算法中，确定了放射源所在空间平面与成像空间平面的关系时，即通过重建算法可以确定放射源与探测器平面之间距离时，是可以对面源进行成像的。

5 结语

通过蒙特卡罗模拟与反投影重建算法可知，康普顿相机的γ光子的利用效率与位置分辨率都优于单孔、编码孔成像γ相机，空间分辨率可以达到FWHM=8.0 mm，角分辨率达到3°，γ光子成像效率达到0.38%，但反投影重建算法存在数据量大、计算时间长等不足。

通过蒙特卡罗模拟获得了设计、制作、改进康普顿相机的理论数据。实际探测器中材料厚度更薄，所以之后工作中需要进一步改进康普顿相机的模拟，研究其性能参数，同时通过采用极大似然法优化重建算法，提高康普顿相机的位置分辨率，进一步为制作生产提供依据。

1 Tdoo R W, Nightingale J M, Everett D B. A proposed γ camera[J]. Nature, 1974, 251: 124−132

2 Mihailescu L, Vetter K M, Burks M T, et al. SPEIR: a Ge Compton camera[R]. Lawrence Livermore National Laboratory, UCRL-TR-202620, March 1, 2004

3 David Peter Thomas Scraggs. Digital signal processing techniques for semiconductor Compton cameras[D]. University of Liverpool, November 2007

4 Mattafirri S. On Compton imaging[D]. UC Berkeley, 2010

5 杨永峰, Gono Y, Motomura S, 等. 一个用于多重示踪技术的康普顿成像装置[J]. 同位素, 2001, 14(3−4): 155−160 YANG Yongfeng, Gono Y, Motomura S, et al. A Compton camera for multitracer technique[J]. Journal of Isotopes, 2001, 14(3−4): 155−160

GEANT4 simulation and imaging reconstruction by backprojection algorithm for Compton camera

DING Changji1,2MAO Benjiang2YUAN Yonggang2JIANG Zhigang2YANG Chaowen1

1(College of Physical Science and Technology, Key Laboratory of Radiation Physics and Technology, Ministry of Education, Sichuan University, Chengdu 610065, China) 2(Institute of Nuclear Physics and Chemistry, China Academy of Engineering Physics, Mianyang 621900, China)

Background: Due to its imaging principle advantages and the development of detectors, nuclear electronics, Compton camera has once again put forward. Purpose: This study aims to build a Compton camera via Monte Carlo simulation and test its backprojection algorithm. Methods: By using Monte Carlo simulation software GEANT4, a Compton camera with stripes structure is designed and data for reconstruction image of source is read out. Backprojection imaging reconstruction algorithm is studied for getting the reconstruction of source. Results: Using backprojection algorithm and simulated Compton camera, when the distance between source and the scattering detector is 40 mm, the spatial resolution is FWHM=8.0 mm, angular resolution is 3° and γ photon imaging efficiency is 0.38%, which are better than most of the pinhole and coded aperture γ camera imaging. Conclusion: Because of the existence of large amount of data, Compton camera needs long calculation time for measuring data. The next step is improving simulated Compton camera to study its performance parameters, while the maximum likelihood algorithm could improve the spatial resolution of Compton camera.

Compton camera, Monte Carlo simulation, Backprojection imaging reconstruction algorithm

TL814，R445.5

10.11889/j.0253-3219.2015.hjs.38.110402

丁长骥，男，1991年出生，2013年毕业于四川大学，现为硕士研究生，主要从事康普顿相机模拟与图像重建

袁永刚，E-mail: yyg_2000@yeah.net

2015-06-24，

2015-09-11

CLC TL814 , R445.5