基于聚类融合的不平衡数据分类方法

禄铠铣

(澳门大学)

0 引言

不平衡数据集的特征就是在数据集里有一种样本的数量大大小于其他的样本数量．对于不平衡数据级来说，使用比较传统的分类手段对其进行分类的话，其结果会十分的倾向多数类，一般来说，人们极为重视少数类，如果少数类被错分，那么付出的代价十分的大，假如将入侵数据看作是正常数据来对待，有极大几率会导致不必要的损失．

在数据挖掘与模式识别等等行业越来越喜欢用聚类算法了．如今聚类算法有很多种，可是，几乎所有的聚类算法都有明显的缺陷．因此，该文使用聚类融合技术，用来让算法更加稳定．

1 基于聚类融合的不平衡数据分类方法

1．1 聚类融合

最近几年内，融合方法大量应用在分类和回归中，而且已经进入到了聚类行业中．Fred A L参考传感器融合与分类器融合的成功经验，发现了新的方法．它的详细定义就是:把一组数据进行聚类的不一样的结果相互融合，而不会使用该数据原来的自身特点．

主要在两个方面进行探究:(1)怎样生成有效果的聚类成员;(2)怎么对共识函数进行设计，让聚类成员能够合并到一起．具体就是聚类成员之间的区别，究竟对聚类融合结果有何影响，是否会影响聚类融合的稳定．聚类融合重点:

如果有包括n个对象的数据集X={x1，x2，…，xn}，使用h次聚类的算法让X数据集能够得到 h 个结果，H={C1，C2，…，Ch}，当中 Ck(k=1，2，…，h)为了可以得出聚类结果重点在于对第k次算法．将h个聚类成员的不同的聚类结果加在一起，然后利用比较专业的共识函数，得出有关结果．

相比于单一算法，聚类融合算法可以得到更好地结果．

(1)鲁棒性:不论是何种领域与数据集，这种方法的平均性能无疑是最强的．

(2)适用性:聚类结果是一般是单一聚类方法不能比拟的．

(3)稳定性与确定性评价:聚类结果有一定的不确定性，可以从融合布局方面来进行评估噪声、孤立点与抽样，这对于聚类结果来说，没有多大的影响．

(4)并行与可扩展性:可以让数据子集并行合并或者是并行聚类，还可以合并分布式的数据源聚类结果或者是数据属性的聚类结果．

1．2 不平衡数据分类方法

机器学习行业的重点探究对象就是分类问题，部分分类方法都日渐成熟，用这些分类方法来对平衡数据进行分类，肯定可以有不错的效果．但是，很多行业里还是有很多不均衡数据及存在的．以往传统分类方法似乎偏向于对多数类有比较高的识别率，少数类识别率则相对比较低．所以，对不均衡数据集有关分类问题的探究，必须要找到一些新的手段与辨别准则．

不平衡数据的分类大致可以分为两种:以数据层面作为基础与将算法层面作为基础的方法．

1．2．1 数据层面的处理方法

数据层面的处理方法就是将数据进行重抽样，包括两种处理办法，分别是过抽样和欠抽样．

一致子集(consistent subset)．

编辑技术(常用的是W ilson．s editing)

以及单边选择(one-sided selection)等［1-2］．

以上技术最重要的是启发性的使用(加权)欧氏距离和K-近邻规则去辨别能够科学删除的样本．Barandela 等人［3］和 Batista 等人［4］都对以上多种欠抽样方法进行了细致的试验与深入的探究．Dehmeshki等人［5］发现了以规则作为基础的数据过滤技术，实际上也属于欠抽样方法．

和欠抽样对立，过抽样技术是想方设法的来让少数类的学习样本增多．最具代表的就是Chawla等人［6］发明的SMOTE 技术．SMOTE 技术理论就是利用插值产生全新人工样本，并不是对样本进行复制．Han等人［7］以此作为参考，发明了Borderline-SMOTE技术．

1．2．2 算法层面的处理方法

根据有关记载，我们得知，如今重点集中在四个不一样的方法，包括代价敏感与单类学习、组合方法和支持向量机方法．

1．3 算法描述

所提出分类算法是将聚类融合的不平衡数据作为基础，就是 CE-Under，CE-SMOTE与CE-SMOTE+CE-Under方法．

2 实验与分析

2．1不平衡数据分类的评价准则

精准度accuracy=(TP+TN)/(TP+TN+FP+FN)是分类问题里经常使用的评估标准(见表1)．

表1 混合矩阵

从上可以得知分类器在数据集的整体分类方面的作用，可是不会发拧出不平衡数据集的分类作用．因此，在不平衡数据方面，必须要制定更为科学的评判标准，经常使用的标准包括:查全率 recall、F-value 值、查准率 precision、G-mean值、AUC．属于少数类 recall、precision、G-mean、F-value值的计算手段如下:

F-value可以说是不平衡数据集学习里比较有效地评判标准，它将Recall与Precision相互组合，当中β是可调参数，一般取值为1．只有在Recall与Precision的值比较大的时候，F-value才会更大，所以它可以准确的反映出少数类的分类作用．另外，G-mean也如F-value一样，是比较有效的评判标准，它是少数类里TP/(TP+FN)和多数类里TN/(TN+FP)的乘积的平方根，当这两者的值都比较大的时候，G-mean才会变得更大，所以G-mean可以科学的评判不平衡数据集的整体分类作用．

2．2 实验结果与分析

在该文里，选择十个少数类与多数类样本比例不均衡的UCI机器学习数据集做实验，每个数据集的基本信息见表2．在表2里，N是样本的数量总和，NMIN是少数类样本的数量，NMAJ为多数类样本的数量，CD是少数类与多数类的样本比例，NA为属性数量(包括类别属性)．

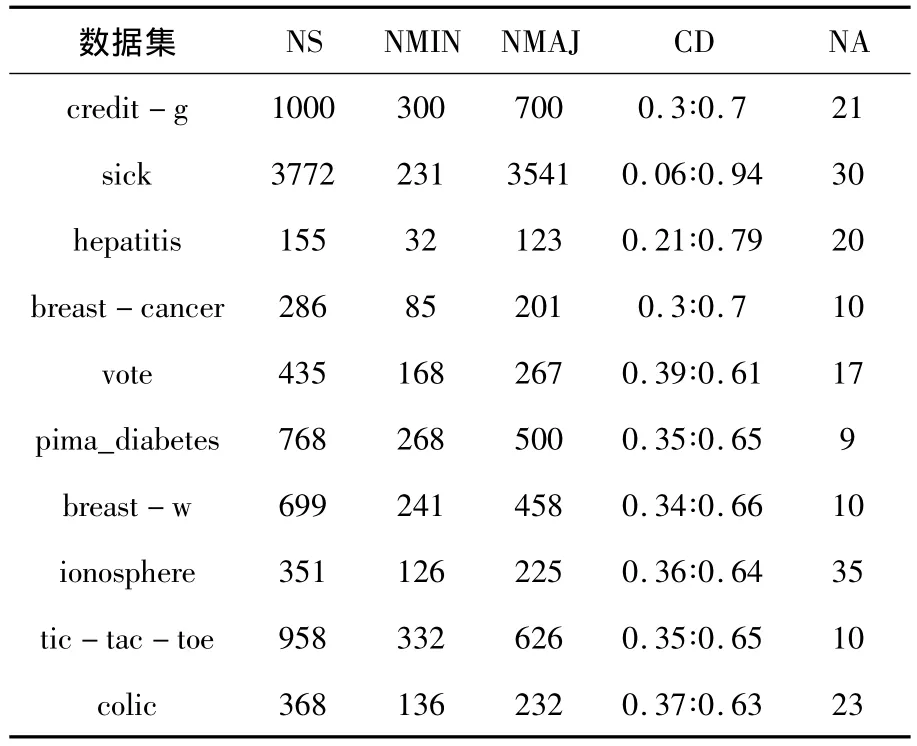
表2 数据集的基本信息

在试验里，与C4．5决策树算法(直接对原数据集进行分类学习)和七类不均衡数据分类方法的作用作比较．上文所述不平衡数据分类方法全部利用C4．5决策树算法，分类学习重抽样后的数据集．

为了能够让上述的不均衡数据分类方法的比较更具客观性，下面全部的实验数据都是10折交叉验证之后得出的结论．

使用weka软件里的Simple Means聚类算法来多次聚类数据．对一致性系数CI阈值α进行聚类，之后取全部样本的平均数值．依据过抽样率与欠抽样率的概念我们可以知道，SMOTE方法产生的合成样本数量和原有少数类样本数量一模一样，就是全部少数类样本数量多出了一倍，而Random Under方法剔除的多数类样本数量则是原有多数类样本的一半．为了能够将过抽样与欠抽样后的数据集作比较，该论文对不平衡程度指标I-degree做出定义，它的数值就是数据集里少数类与多数类样本的比值，I-degree的值越高代表着数据集里少数类样本数量越大，多数类样本的数量越少．当I-degree值几乎等于1的时候，代表着数据集里面的多数类与少数类的样本数量比较均衡．图1显示十个UCI的初始数据集OldDataSet和使用CE-SMOTE+CEUnder，CE-SMOTE与CE-Under方法进行重抽样之后数据集的I-degree值，而且每种I-degree值全部经过10折交叉验证之后得出的结论．从图1我们可以知道，该论文所提出的CESMOTE+CE-Under、CE-SMOTE 与 CE-Under方法都能够让数据集不平衡的程度有所降低．因为CE-SMOTE+CE-Under方法可以对少数类与多数类同时做处理，所以进行重抽样之后数据集I-degree值是最高的，而CE-SMOTE方法的I-degree值稍微高于CE-Un-der方法的I-degree值．

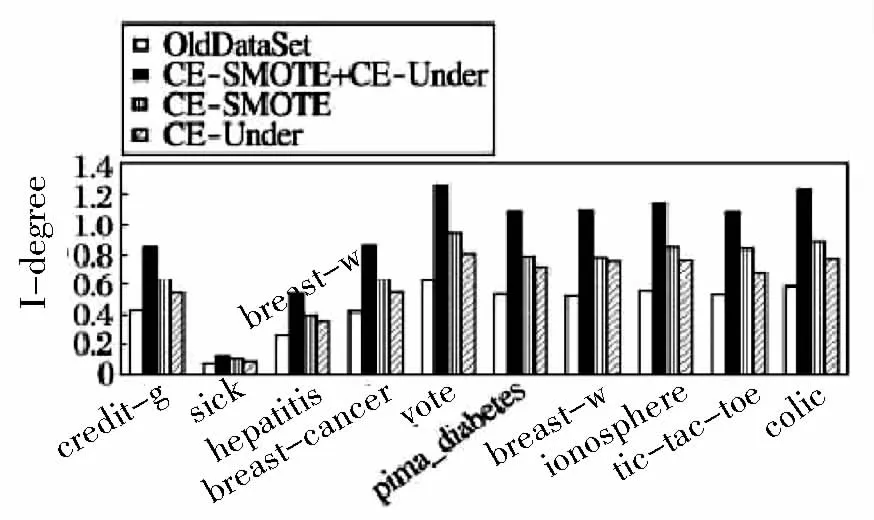
图1 10个数据集的I-degree值

表3 8种方法在10个UCI数据集的少数类F-value值对比

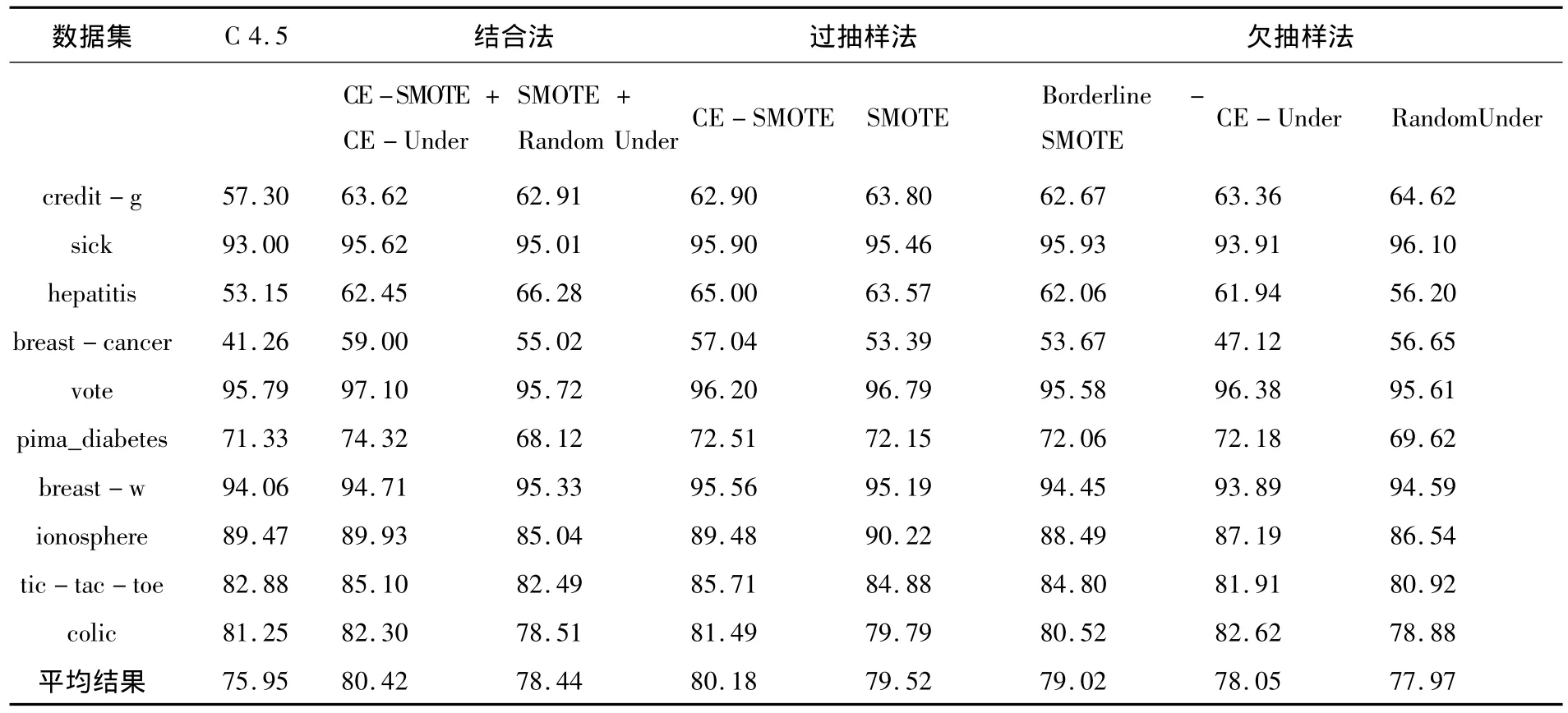
表4 8种方法的G-mean值对比

表3与表4分别列举了8种方法在十个UCI数据集上的少数类F-value值与数据集总体的G-mean值．而表中最底部的一行则列举出了每一个方法在全部数据集里的平均结果．对于每一个数据集来说，分别得来对结合法、过抽样法与欠抽样法里每一种方法的F-value与G-mean值做对比，同时用黑体字来代表这三种方法里最高的F-value与G-mean值．

从表3与表4当中可以知道，上文提到的七类不平衡数据分类方法的少数类F-value值与数据集总体的G-mean值比原始数据集进行分类的C4．5算法都要高．．

三种方法经过横向对比可以得出如下结果，结合法里面的CE-SMOTE+CE-Under方法很显然要比SMOTE+RandomUnder方法更加优秀，而欠抽样法里面的CE-Under方法一般来说要比Random Under方法更具优势．把三种方法进行纵向对比，我们得出的结论是，过抽样法与结合法作比较，欠抽样法则更具优势，同时结合法与过抽样法的少数类F-value值与G-mean值相对比较大，综上所述，上文提出的这些方法都是极为优秀的方法．

总之，该论文提到的有关基于聚类融合的不平衡数据分类方法的识别率相对较高，特别是对于部分少数类和部分数据集总体也有着不错的识别率．通过一系列的实验，并且对比各个实验数据，我们可以得出以下的结论，CE-SMOTE+CE-Under方法与CE-SMOTE方法对不平衡数据集的分类作用比较强，CE-Under方法则相对较弱，但是它的对比算法与其他的算法相比更具优势，这类方法的优势还是比较多的，不论在不一样的过抽样率、还是不一样的欠抽样率下乃至是聚类次数下，这种方法的少数类F-value值总是十分的稳定．综上所述，笔者提出的有关基于聚类融合的不平衡数据分类方法在不同条件下都可以良好降低数据集的不平衡程度，同理，在数据集整体G-mean值不下调的情况下，可以让少数类的F-value值有所提升，这对多数类和少数类的均值都有不错的识别率．

［1］ Batista G E A P A，Pratir C，MONARDM C．A study of the behavior of several methods for balancing machine learning training data［J］．Slgkdd Explorations，2004，6(1):20-29．

［2］ KuBatm，Matwin S．Addressing the curse of imbalanced training sets:one-sided selection［C］//Proc of 14th International Conference on Machine Learning(ICML．97)．Nashville:［s．n．］，1997．179-186．

［3］ Barandela R，Valdovindos R M，Snchez J S，et al．The imbalanced training sample problem:under or over sampling［C］//Proc of International Workshops on Structura，l Syntactic，and Statisti cal Pattern ecognition(SSPR/SPR．04)．Lisbon:［s．n．］，2004，806-814．

［4］ Batista G E A P A，Pratir C，Monardm C．A study of the behavior of several methods for balancing machine learning training data［J］．S IGKDD Explorations，2004，6(1):20-29．

［5］ Dehmeshki J，Karak Y M，Casique M V．A rule-based scheme for filtering examples from majority class in an imbalanced training set［C］ //Proc of MLDM，2003．215-223．

［6］ Chawlanv，Halllo，Bowyer K W，et al．Smote:synthetic minority over sampling technique［J］．Journal of Articial Intelligence Research，2002，16:321-357．

［7］ Han H，Wang Wenyuan，Mao Binghuan．Borderline-SMOTE:a new over-sampling method in imbalanced data sets learning［C］ //Proc of International Conference on Intelligent Computing(ICIC．05)．Hefe:i［s．n．］，2005．878-887．