基于空间约束的舰载机出库调度
2015-12-02王云翔毕玉泉杨茂胜王虹昙
王云翔,毕玉泉,杨茂胜,王虹昙
(海军航空工程学院青岛校区,山东 青岛 266041)
舰载机在航母上的布列,主要集中于两个区域:一是航母宽大的飞行甲板,二是舰体内部的大型机库。在飞行甲板上布列的舰载机数量决定了航母第一波次的攻击能力。但大型海战的经验告诉我们,航母的连续攻击能力更加重要,如中途岛海战等,都是因为第二、第三攻击波次调度不利,导致战役的失败。航母的连续攻击能力,很大程度上取决于舰载机在机库与飞行甲板之间的调度优化,即怎样在最短时间内将指定的舰载机从机库转运到飞行甲板机务停机位。目前,国内一些学者已经在做舰载机调度优化方面的研究。冯强针对舰载机航保系统的动态调度问题,给出了相应的约束条件,并应用Multi-agent技术建立了模型[1]。魏昌全针对舰载机连续出动情况下航保重调度问题和在空间约束情况下的舰载机航保调度问题建立了两种模型[2-3]。李耀宇采用排队论和逆向强化学习方法建立了两种舰载机飞行甲板调度的模型[4-5]。司维超在考虑舰载机出动时间情况下建立了舰载机由飞行甲板停机位到起飞位的调度模型,并计算出了各种方案的出动时间[6]。
以上研究主要集中于舰载机在飞行甲板的调度,主要考虑问题是航空母舰航保系统的资源分配,而对舰载机在航母上任意停机位之间的调度问题还少有研究。本文以俄罗斯现役航空母舰为研究对象,主要针对舰载机从航母机库内指定停机位转运到飞行甲板指定停机位的调度问题进行研究,建立转运方案的数学模型,利用智能粒子群算法对该问题进行求解,给出最优方案。
1 舰载机出库问题
1.1 出库需求分析
舰载机在起飞前都要在机务停机位进行准备工作,如图1所示。当第一波次舰载机出动完毕后,需要从机库内将后续舰载机转运到飞行甲板机务停机位,如图2所示,在飞行甲板机务停机位准备后,滑向起飞位,这就是第二攻击波次,以此类推。这里涉及两个问题:一是舰载机的布列,舰载机在飞行甲板的布列要考虑到机务准备设备的位置,要便于操作,不能远离设施,同时也不能过于紧密,避免进出停机位困难;二是舰载机的转运,舰载机转运要统筹兼顾,考虑转运距离,合理利用转运设施,同时开展作业,以最大程度节省时间。

图1 飞行甲板停机位

图2 机库甲板停机位
对于舰载机的布列,主要由指挥员确定,根据当时飞行甲板面的设备分布情况,根据起飞位设备的需求等情况确定。当舰载机布列确定后,也就是从哪些机库停机位转运到哪些飞行甲板停机位确定后,就要考虑舰载机转运的问题,即怎样合理利用转运设施,包括牵引车、调向转盘和升降机等,在最短时间内将一个波次内的舰载机转运到位。
1.2 出库流程分析
本文以一次四机出动为例进行分析,机库内的A、B、C、D四架舰载机分别转运到飞行甲板的 E、F、G、H四个停机位。转运过程做一个基本假设:机库内停放两辆牵引车,飞行甲板停放两辆牵引车,且牵引车不随升降机转运。
1)A舰载机与D舰载机同时开始解系留转运,A机到达一号调向转盘后进行系留、转向、解系留,到达一号升降机后进行系留。同时D机到达二号调向转盘后进行系留、转向、解系留,到达二号升降机后进行系留。
2)当A机在一号升降机系留后,牵引车返回B停机位,B机开始解系留,驶向调向转盘,进行系留、转向、解系留,到达一号升降机后进行系留。
3)当D机在二号升降机系留后,牵引车返回C停机位,C机开始解系留,驶向调向转盘,进行系留、转向、解系留,到达二号升降机后进行系留。
4)B机在机库内转运的同时,A机随升降机上升到飞行甲板,解系留后,由牵引车牵引到E号停机位系留。牵引车返回升降机待命。
5)C机在机库内转运的同时,D机随升降机上升到飞行甲板,解系留后,由牵引车牵引到H号停机位系留。牵引车返回待命。
6)B机随升降机到达飞行甲板,解系留,并转运到F停机位系留。
7)C机随升降机到达飞行甲板,解系留,并转运到G停机位系留。
以上是没有经过优化的出库流程,不一定是最优过程。其优化主要体现在两个方面:一是资源分配问题,整个流程涉及到4个设备,两个调向转盘两个升降机,由于调向转盘与升降机位置固定,因此,选定调向转盘后,升降机不用再选择,即资源分配时只需要分配调向转盘;二是作业次序问题,对于同一个调向转盘,要给出最优的舰载机队列方案。同时,在优化中还要考虑空间约束问题,即舰载机停机位的路径距离,由于牵引速度较慢,设备运行时间短,所以在舰载机调度过程中运动时间不可忽略。综上可以看出,基于空间约束的舰载机出库问题,可以转化为考虑空间约束的柔性流水车间优化问题。
2 基于空间约束的舰载机出库模型
2.1 假设条件
为建立舰载机出库调度模型,本文作如下假设:1)所有舰载机在调度开始时可用,无封闭障碍,所有转运设备可用,调度过程中不损坏;2)牵引作业一次到位,无调整时间;3)牵引车负载作业和空驶作业速度一定且相等;4)所有舰载机保障工艺相同,全部要经过调向转盘调整;5)舰载机所有停机位已知,且固定;6)同一时刻一台设备只能保障一架舰载机;7)同一时刻一架舰载机只能接受一个阶段一台设备的保障。
2.2 参数说明
文中,F为所要达到的目标函数,即最优方案为最后一架舰载机调度完工时间最短的方案;Tp(i)为第P套方案中,第i停机位舰载机的调度完工时间;Ts(i,j,k)为机库内第i停机位舰载机处于第j顺序到达k号升降机系留结束的时间;Tj(i,j,k)为机库内第i停机位处于第j顺序到达k号升降机的舰载机的开始转运时间;A[m,k]为常数矩阵,是机库内牵引车由第m停机位空驶到k号升降机的需用时间;B[i,k]为常数矩阵,是飞行甲板上第i停机位舰载机到第k号升降机的转运需用时间;B(m,j,k)以第j顺序升起后的舰载机由k号升降机到第m号飞行甲板停机位的转运时间;C[i,k]为常数矩阵,是机库内第i停机位舰载机到第k号升降机系留完毕需用时间;C(i,j+1,k)为在第i停机位的舰载机,以第j+1顺序到达k号升降机的转运时间;Tsj为升降机单程升降需用时间;Tt舰载机系留或解系留的需用时间;a(i,j,k)为机库内第i停机位处于第j顺序到达第k号升降机的舰载机的标号。
2.3 调度模型
舰载机出库调度模型如下。
目标函数:
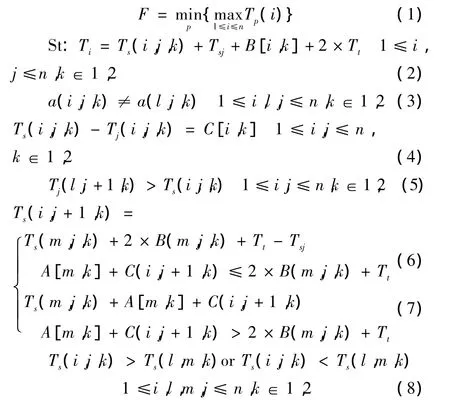
式(1)表示目标为求取舰载机总调度完工时间最短的方案;式(2)表示处于第i初始停机位的舰载机转运过程不中断,保持转运连续性;式(3)表示不同舰载机的初始停机位不同且已知。式(4)表示在考虑空间约束情况下,第i停机位舰载机到k号升降机的转运时间确定。式(5)表示舰载机保障转运属于串行工序,只有前一工序完成后,下一道工序才能开始。式(6)、(7)表示考虑串行工序的等待时间,将串行工序的等待时间计算到转运时间内。式(8)表示同一设备不能保障多架舰载机。
3 出库调度问题的粒子群算法
3.1 智能粒子群算法
智能粒子群算法是一种基于群智能的优化算法,初期用于无约束条件的连续函数优化问题,经进一步发展后,提出了离散型的智能粒子群算法[7-8]。该算法可用来求解复杂的组合优化问题,每个优化方案都可编码为搜索空间的一个粒子,每个粒子在解空间中都有一个位置和一个速度值,而且可以通过目标函数计算它的适应值,通过粒子的适应值可以找到个体最优粒子和全局最优粒子。所有粒子通过追随这两个最优粒子的运动,逐渐趋于收敛,从而找到最优组合。
粒子群算法数学表达如下:

其中:xi=(xi1,xi2,…,xid)为粒子群中第i个粒子在d维空间中的位置;vi=(vi1,vi2,…,vid)为粒子群中第i个粒子在d维解空间中的速度;pi=(pi1,pi2,…,pid)为粒子群中第i个粒子的个体历史最优值:pg=(pg1,pg2,…,pgd)为所有迭代中的全局最优粒子;t为迭代次数;w 为惯性因子;c1,c2为学习因子;rand1,rand2为[0,1]之间均匀分布的随机数。舰载机出库调度问题是一种组合优化问题,具有离散、动态的特点,应用智能粒子群算法求解时,需要注意粒子的编码问题。
3.2 粒子的编码与解码
可以把每种舰载机出库调度方案作为一个粒子,而每种方案实际上要解决两个问题,也就是前面所说的资源分配和作业次序,因此本文采用二维粒子进行方案的编码[9-10]。对于一次L架舰载机的转运,第一维L个向量表示各架舰载机的转运作业次序,第二维L个向量用于分配各架舰载机需要占用的资源。如果以10架舰载机,2套调向转盘为例,那么第一维数据可在-10与10之间取随机数,第二维数据在1与3之间取随机数,第i个粒子可由表1表示。

表1 第二维数据第i个粒子
对于处于10个停机位的舰载机,粒子位置向量Xi表示了10架舰载机的作业次序,数值越小的,作业次序越靠前。粒子位置Yi表示了10架舰载机的分配哪个转盘。粒子解码过程如下。
1)资源分配。对第二维粒子Yi进行向零取整操作Fix(Yi),如表2,即可得到哪架舰载机分配哪个转盘,本例中有两套转盘,因此Yi取值范围是[1,3)。

表2 第二维粒子Yi向零取整结果
2)作业次序。按照资源分配后的序号,依次解码出每个转盘对应舰载机位置,然后按照第一维粒子Xi的数值大小进行排序,数值越小的作业次序越靠前,从而解码出每台设备的舰载机队列。因此,上面表格中的舰载机队列为:
转盘1:3→1→8→4 转盘2:9→6→10→5→7→2。
3.3 参数设置
粒子速度公式中,学习因子分别调节向个体最优粒子和全局最优粒子飞行的步长,本文分别取值为c1=1.7,c2=2。惯性因子w决定了粒子的搜索范围,前期取值较大确保算法的全局性,后期取值较小确保收敛精度高。本文采用带收缩因子和线性递减权重的粒子群优化算法[11],惯性因子取值为

速度更新公式[12]为
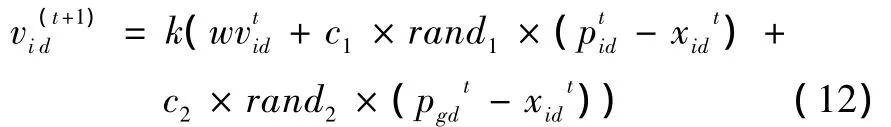
3.4 算法步骤
1)算法初始化,设置迭代的最大次数,粒子群数量,初始化种群的位置和速度,注意各粒子的位置边界与速度边界。
2)对粒子解码生成调度方案,根据舰载机作业次序通过目标函数计算适应值。对于超过约束条件的粒子,将其适应值设置为无穷大,从而淘汰不合理方案。根据粒子适应值,将每个粒子所有经历位置中最好的设置为个体最优粒子,将所有粒子所有经历位置中最好的设置为全局最优粒子。
3)由式(12)、(10)对粒子的速度和位置进行更新。
4)更新后的粒子,如果速度超过了边界,则按边界值取。如果位置超过了边界,则位置取边界值,速度取相反方向,使粒子向回飞。
5)判断迭代条件,如果是,输出结果,如果不是,转向步骤2)。
4 仿真结果
本文采用Matlab7.1编程,以机库内10架舰载机向飞行甲板转运,前后各一套调向转盘、一套升降机,飞行甲板两台牵引车,机库两台牵引车为例。对于仿真中机库内转运、飞行甲板转运和机库内空驶三组时间参数矩阵,由于航母上所有机库停机位和飞行甲板停机位固定,可在实地测量后给出。本文重在方法研究,其时间矩阵由图纸上缩比测量后,按照机库内3km/h,飞行甲板5km/h的速度,计算后给出,其参数矩阵参见表3。
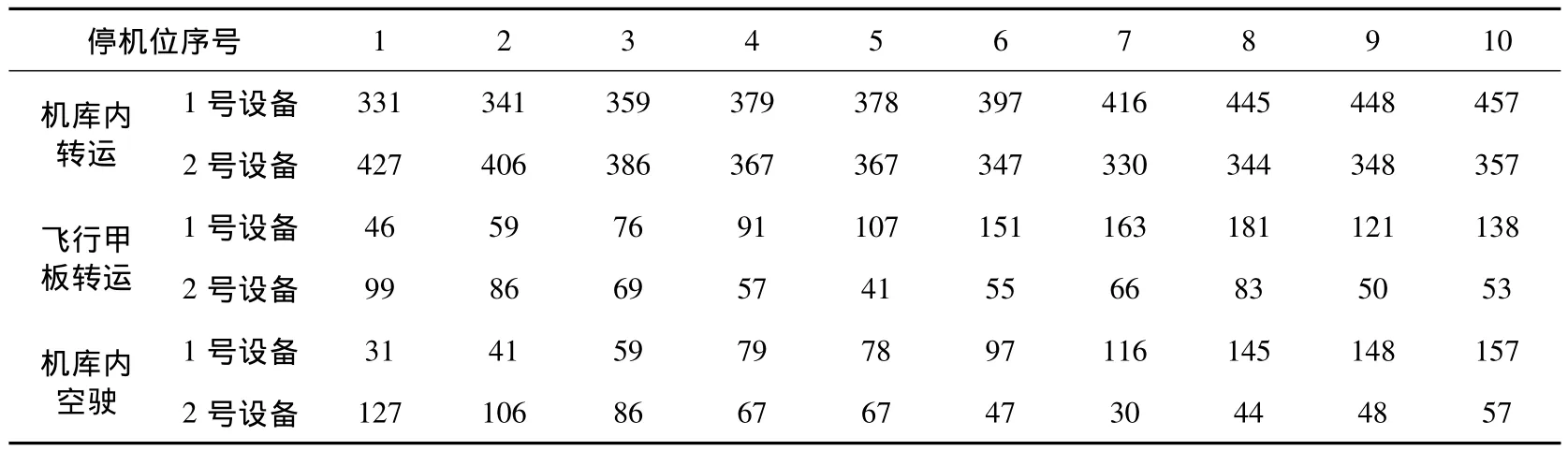
表3 参数矩阵
设置粒子群种群数量为20,最大迭代次数为200,连续优化10次,得到计算结果如表4所示,10次中最优结果的收敛过程如图3所示。从仿真结果可以看出:
1)在不考虑调整时间条件下,十架舰载机出库最短用时1850s,其对应的转运方案为
转盘1队列:5→3→1→2→4
转盘2队列:6→7→8→9→10;
2)十次优化中,初始随机方案调度用时最多在2300s以上,最优结果可节省转运用时450s左右,占总用时近20%,因此调度优化具有较大应用价值。

图3 最优结果收敛过程

表4 仿真计算结果
3)智能粒子群算法应用于在空间约束条件下的舰载机出库问题时,收敛速度较快,10次优化过程全部在30次迭代内完成,在多次仿真情况下,最优值相差不大,基本没有陷入局部收敛,说明智能粒子群算法能够较好地解决这类问题。
4)本仿真算例中停机位分布均匀,所得最优结果没有出现资源抢占问题,每台调向转盘平均分配5架舰载机。但当初始停机位或目标停机位分布不均时,可能会出现资源抢占,本文数学模型能够较好解决这类问题,限于篇幅原因,这里不再列举具体算例。
5)本文十架舰载机转运最优时间在31min左右,与实际转运时间有一定差距,其主要原因是舰载机转运中在临时停机位的停车调整时间,但调整时间人为因素较大,预测难度大。本文所述方法重在解决资源分配和作业次序问题,转运总用时只作为指挥员参考。
5 结束语
本文以俄罗斯航母在空间约束条件下舰载机出库调度问题为研究对象,分析了制约其出库调度速度的原因,梳理了舰载机出库调度流程,建立机库内舰载机出库调度的模型,设计求解模型的智能粒子群算法,通过仿真,验证了模型算法的可行性及有效性,给解决这类出库问题提供了一种方法。
[1] 冯强.不确定条件下舰载机动态调度仿真与优化方法[J].系统仿真学报,2011,23(7):1497-1506.
[2] 魏昌全,陈春良,王保乳.基于任务的连续出动舰载机航空保障重调度研究[J].指挥控制与仿真,2012,34(3):23-26.
[3] 魏昌全,陈春良,王保乳.基于空间约束的舰载机航空保障调度研究[J].控制工程,2013,20(4):701-706.
[4] 李耀宇,朱一凡,杨峰,贾全.基于逆向学习的舰载机甲板调度优化方案生成方法[J].海军工程大学学报,2013,35(4):171-175.
[5] 李耀宇,朱一凡,贾全,李群.基于排队网络的舰载机甲板调运优化调度策略生成方法[J].国防科技大学学报,2013,25(5):26-30.
[6] 司维超,韩维,史玮韦.基于PSO的舰载机舰面布防调度方法研究[J].航空学报,2012,33(11):2048-2056.
[7] KENNEDY J,EBERH ART R C.A discrete binary version of the particle swarm algorithm[C]∥Proceedings of 1997 Conference on Systems,Man,and Cybernetics.Washington,D.C.,USA:IEEE,1997,5:4104-4108.
[8] LIAO C J,TSENG C T,LUARN P.A discrete version of particle swarm optimization for flowshop scheduling problems[J].Computers & Operations Research,2007,34(10):3099-3111.
[9] 刘志雄.基于粒子群算法的物流配送车辆优化调度研究[J].物流技术,2009,32(6):615-618.
[10] WANG LAIJUN,SHI ZHONGKE,LEI XIUJUAN.Dynamic tabu search algorithm for solving departure scheduling problem[J].Journal of southwest jiotong University(Endlish Edition),2007,15(2):132-137.
[11] 粒子群优化算法[EB/OL].http:∥www.ipic.njupt.edu.cn/neoxus/index.php,2009-04-28.
[12] EBERHART R C,SHI Y.Comparing inertia weights and constriction factors in Particle Swarm Optimization[C]∥Proceedings of the Congresson Evolutionary Computating,2000:84-88.
