舰炮一维修正弹校正诸元误差和预测误差试射

黄 义，汪德虎，杨绍清

(海军大连舰艇学院，辽宁 大连 116018)

一维弹道修正弹是为提高密集度采用阻力修正原理进行纵向距离修正的一种新型弹药［1］。虽然一维弹道修正弹能够提高纵向密集度，但是射击诸元精度不能通过修正来提高，而且射击诸元误差不能像传统无控弹一样通过测量弹着点相对目标或提前点偏差来获取和校正。一方面，射击诸元误差会使中央弹着点偏差目标或提前点;另一方面，根据一维弹道修正弹“打远修近”原理［2-3］，如果不对射击诸元误差进行校正，则必须增加更多的射程扩展量［4］。由此带来两个问题:其一，修正后最大射程减小;其二，射程修正量增大、修正机构工作时间增长，则修正机构工作误差增大，导致落点精度减小。由于一维弹道修正弹工作原理与无控弹不同，射击误差组成以及对弹着点偏差的影响也不同，舰炮使用无控弹试射方法不适于一维弹道修正弹。为提高射击精度和作战效能，针对一维弹道修正弹工作原理，分析射击误差，研究试射新方法。

1 试射必要性

1.1 射击误差分类

舰炮使用一维弹道修正弹对目标或提前点射击主要存在如下射击误差:

1)射击诸元误差，主要为弹道气象误差，指计算射击诸元使用的弹道气象条件与实际的弹道气象条件不一致，导致射击诸元确定的弹道与发射后实际弹道不一致。弹道误差主要包括初速、弹重、阻力系数等，气象误差主要包括虚温、气压和风。

2)预测落点误差，指火控根据跟踪雷达观测弹丸飞行一区段样本值，按照弹道预测方程预测弹丸落点，如果不对后续飞行弹道进行修正，该飞行弹丸实际落点与预测落点不重合，称此误差为预测落点误差。预测误差，包括观测弹道误差和预测模型误差。观测弹道误差包括两个方面:一为雷达测量弹道的测量误差;二为我舰姿态导航误差，包括航速测量误差、航向测量误差、摇摆角测量误差和升沉测量误差［5］。

3)修正机构工作误差，指实际射程修正量与预计射程修正量之间的误差，主要由阻力环张开时间误差和阻力环外形尺寸误差产生。

1.2 试射必要性

由于弹道气象误差、预测落点误差以及修正机构工作误差的存在，导致修正后实际落点与目标或提前点不一致、产生偏差。如图1所示，O点为发射点，OX表示射击方向，P点为提前点，C点为实际弹着点，Sn点为预测修正执行机构不工作的弹着点，Cn点为假设修正机构不工作的弹着点。PCn为射击偏(误)差，包括射击诸元误差(中央弹着点相对提前点偏差)和散布误差，CnSn为预测误差，(CnSn-CP)为修正误差。由于Cn点未知，所以，必须通过试射让修正机构不工作，获取诸元误差和预测误差，再对二者进行校正以提高射击精度。

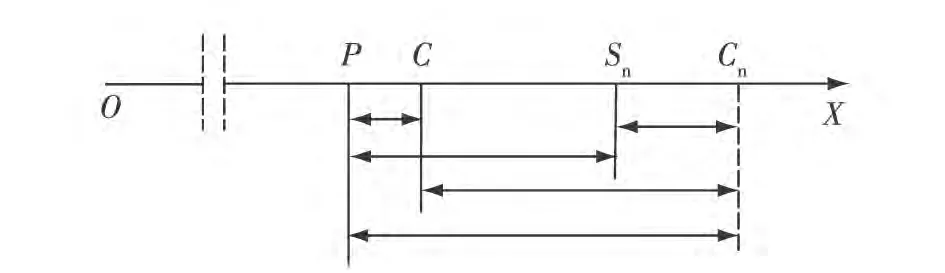
图1 射击偏(误)差、预测误差和修正误差示意图

事实上，校正诸元误差和预测误差试射，P点、Sn点和Cn点不一定在一条直线上。以对海上运动目标射击为例，如图2所示，O为发射点，Mt为目标现在点，P为计算的提前点，V为滤波求取的目标速度，→S=MtP为计算的目标运动提前量，→Dt=OMt为目标现在距离向量，→Dp=OP为计算的目标提前距离向量;Sn点为根据实测弹道预测落点，Cn点为实际落点，CnSn为预测误差，PCn为射击偏(误)差，包括射击诸元误差(中央弹着点相对提前点偏差)和散布误差;S'n为直线OP上一点、满足 OS'n=OSn，C'n为直线 OP上一点、满足OC'n=OCn，C'nS'n为预测落点的距离误差，PC'n为距离上的射击偏(误)差;∠CnOSn为预测落点的角度误差，∠CnOP为角度上的射击偏(误)差。

图2为发射一发无控弹的情况，由于随机误差的存在，需要发射多发弹，求取每一发的射击偏(误)差和预测误差，计算其平均值用于射击校正。

2 试射方法

2.1 诸元误差的求取与校正

2.1.1 求取诸元误差

如图3所示，P点为提前点，o'为中央弹着点，Cn点为一发弹实际落点，以一发弹实际观测弹着水柱与提前点的偏差作为发射诸元误差的精度为Δd1+Δd2，Δd1表示修正弹不修正时弹着散布误差，Δd2表示观测实际弹着水柱与提前点偏差的测量误差。

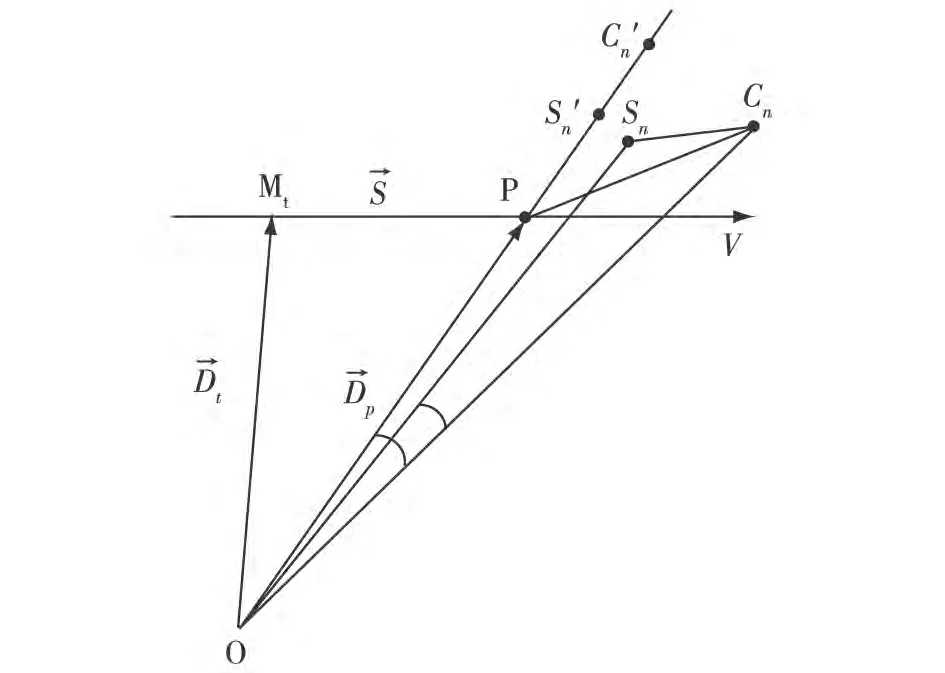
图2 射击偏(误)差和预测误差示意图

图3 求预测误差确定发射诸元误差精度示意图

设以n发弹实际观测弹着水柱与提前点的偏差平均值作为发射诸元误差的概率误差为EdCn，则

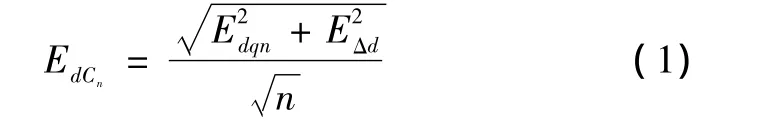
式中，Edqn为不修正时弹着散布误差的概率误差，EΔd为测量误差的概率误差。

表1列出了发射不同发数时，以实际观测弹着水柱与提前点的偏差平均值作为发射诸元误差的概率误差。

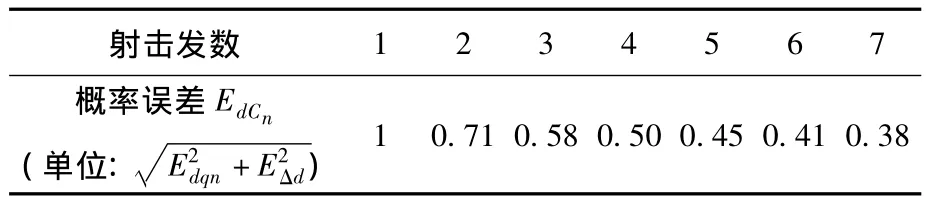
表1 以实际观测弹着水柱与提前点的偏差平均值作为发射诸元误差的概率误差

从表1可以看出，随着射击发数的增加，以实际观测弹着水柱与提前点的偏差平均值作为发射诸元误差的概率误差将减小;但是，射击发数愈多，概率误差减小得愈不显著。

2.1.2 校正诸元误差

1)校正距离误差

诸元误差主要是弹道气象误差，当弹道气象条件一定时，弹道气象修正量的大小随射击距离的不同而不同，弹道气象修正量的误差也随射击距离而改变。若将测得的平均距离偏差量直接在距离上校正，那么射击距离的改变将会使射击诸元产生新的误差。

最精确的校正方法是将因初速、弹重、空气密度、风等误差引起的距离偏差量，从测得的距离偏差量中分离出来，分别进行校正，但是在实际中无法实现。因为一方面难以确定各误差源大小，若能确定也不需要试射，射击准备时直接修正就可以;另一方面，即使能确定各项误差，分别校正也较为复杂、用时较长。由于初速或空气密度偏差引起的距离偏差与各弹道气象条件误差综合引起的距离偏差，随距离的变化规律相似，所以，可以只折合成初速或空气密度偏差进行校正。对于装有初速测量雷达的舰炮武器系统，由于可以通过实际测量初速获取初速误差，则可以折合成空气密度偏差进行校正。

2)校正方向误差

校正方向上诸元误差的方法是将测得的平均方向偏差量按相反符号直接加入方向瞄准角中。校正方向偏差之后，随着射击距离的变化可能会出现新的误差，但由于方向上的误差积累较慢，校正一次可以保持在一次射击中不会出现新的方向偏差。

2.2 预测误差的求取与校正

2.2.1 求取预测误差

如图4所示，Sn为一发弹的预测落点，S'n表示如果对本发弹进行多次测量、多次预测，预测落点的平均值，Cn点为一发弹实际落点，以一发弹预测弹着落点与实际观测弹着水柱的偏差作为预测误差的精度为Δd1+Δd2，Δd1表示预测误差的散布误差，Δd2表示观测实际弹着水柱的测量误差。

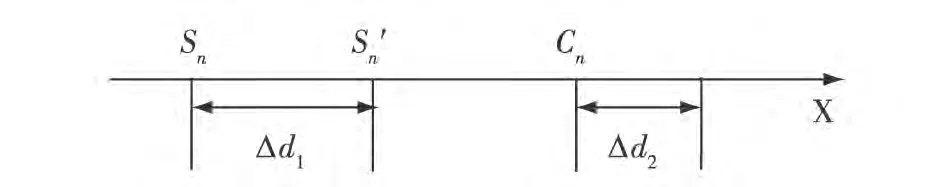
图4 约定预测误差精度示意图

设以n发弹预测弹着落点与实际观测弹着水柱的偏差平均值作为预测误差的概率误差为EdS，则

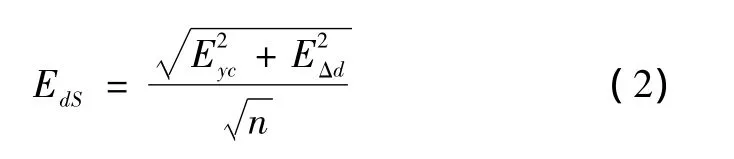
式中，Eyc为预测误差的概率误差，EΔd为测量误差的概率误差。

与求取诸元误差类似，随着射击发数的增加，以预测弹着落点与实际观测弹着水柱的偏差平均值作为预测误差的概率误差将减小;但是，射击发数愈多，概率误差减小得愈不显著。

2.2.2 校正预测误差

由于预测落点误差源较多，并且对预测落点偏差的影响规律不尽相同，所以，对预测落点误差的校正方法采用距离和方向上均取相反符号的方法直接校正［5］。

2.3 试射发数的确定

试射发数的确定考虑3个因素:1)随着射击发数的增加，以实际观测弹着水柱与提前点的偏差平均值作为发射诸元误差的概率误差将减小，以预测弹着落点与实际观测弹着水柱的偏差平均值作为预测误差的概率误差也将减小;但是，射击发数愈多，概率误差减小得愈不显著。2)由于未进行弹道修正，落点相对提前点偏差较大，未能发挥弹道修正弹落点精度高的优势。3)试射时间不易长、试射发数不易多，因为试射发数越多，持续时间越长，目标将做更多的规避机动和火力反击。综上考虑，求取诸元误差和预测误差对海上运动目标试射的射击发数取3～6发较为合适。

3 仿真分析

假设弹道误差:初速误差均值 3.0m/s、均方差0.5m/s，弹重误差均值 100g、均方差 20g，弹道系数误差均值和均方差为标准值的0.5%;气象误差为:虚温误差均值和均方差为0.1°K，气压误差均值和均方差为0.1%p0N，风误差均值 3.0m/s、均方差 0.3m/s;预测误差:雷达测距误差均值和均方差为10m，雷达测角误差均值和均方差为1.0mrad，舰艇摇摆角测量误差均值和均方差为1.0 mrad，舰艇航速测量误差均值和均方差为0.8Kn，舰艇航向测量误差均值和均方差为 1.0 mrad;修正误差:阻力环打开时间误差均值和均方差为1ms。舰炮使用一维修正弹对射程25km、纵深和横宽均为50m的目标射击，试射发射6发，采用Monte-Carlo法仿真10000次。试射后单发命中概率和不试射单发命中概率如表2所示。

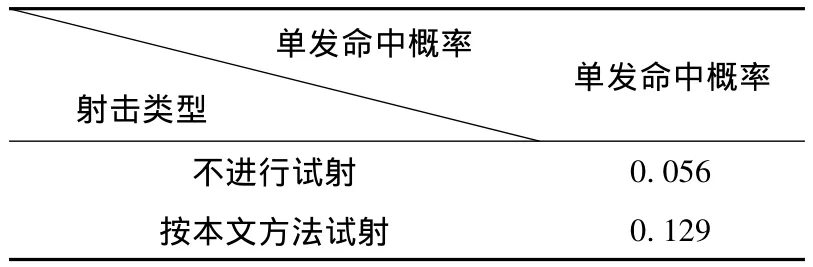
表2 不试射和试射单发命中概率对比表

从表2可见，按本方法试射能够提高射击精度。

4 结束语

舰炮使用一维弹道修正弹射击误差主要包括射击诸元误差、预测落点误差和修正机构工作误差，由于各项误差的存在，导致修正后实际落点与目标或提前点不一致、产生偏差，而且无法从弹着点偏差中分离各项误差进行射击校正。本文提出的舰炮使用一维弹道修正弹，通过让修正机构不工作获取诸元误差和预测误差，再从距离上和方向上进行校正的试射新方法能够显著提高射击精度。

［1］ 陶陶，王海川.一维弹道修正弹阻力环修正控制算法研究［J］.指挥控制与仿真，2009，31(3):88-90.

［2］ 史金光，王中原，曹小兵.一维弹道修正弹气动力计算方法和射程修正量分析［J］.火力与指挥控制，2010，35(7):80-83.

［3］ 王中原，史金光，李铁鹏.弹道修正中的控制算法［J］.弹道学报，2011，23(2):19-21，27.

［4］ 黄义，汪德虎，由大德.一维弹道修正弹对海上目标射击误差及射程扩展量研究［J］.弹箭与制导学报，2012，32(1):149-151.

［5］ 黄义，汪德虎，余家祥.舰炮一维弹道修正弹射击误差分离和校正研究［J］.指挥控制与仿真，2012，34(3):44-46.