Impact of bridge pier on the stability of ice jam*

WANG Jun （王军）， SHI Fa-yi （施发义）， CHEN Pang-pang （陈胖胖）， WU Peng， SUI Jueyi. College of Civil and Hydraulic Engineering， Hefei University of Technology， Hefei 0009， China，E-mail：wangjunhfut@6.com. Dongfeng Motor Corporation Technical Centre， Wuhan 40058， China. Environmental Engineering Program， University of Northern British Columbia， Prince George， BC， Canada

Impact of bridge pier on the stability of ice jam*

WANG Jun （王军）1， SHI Fa-yi （施发义）2， CHEN Pang-pang （陈胖胖）1， WU Peng3， SUI Jueyi3
1. College of Civil and Hydraulic Engineering， Hefei University of Technology， Hefei 230009， China，
E-mail：wangjunhfut@126.com
2. Dongfeng Motor Corporation Technical Centre， Wuhan 430058， China
3. Environmental Engineering Program， University of Northern British Columbia， Prince George， BC， Canada

（Received September 23， 2014， Revised November 12， 2014）

River ice jam is one of the most important issues in rivers in cold regions during winter time. With the extra solid boundary due to the ice cover， the flow condition under ice-covered conditions is completely different from that of a open channel flow. The presence of bridge piers will further change the velocity field around the bridge piers. As a consequence， the formation and the accumulation of ice jams in the vicinity of the bridge pier will be affected. On the other side， the formation of an ice jam around the piers can cause extra turbulence to reduce the stability of a river bridge. The present study focuses on the stress analysis of the ice jam in the vicinity of a bridge pier. By developing a governing equation for describing the equilibrium state of an ice jam， the stability of the ice jam around bridge piers is analyzed and determined. As seen from the field data in literature， the stability estimations of an ice jam around bridge piers determined by the present method agree well with the field observations. Therefore， the proposed approach can be used for the prediction of the formation of ice jams around bridge piers.

bridge pier， ice jam， stress analysis， equilibrium state， stability analysis

Introduction0F

River ice jam is one of the most important hydraulic issues in cold region during winter. As the ice jam adds an extra solid boundary to the flowing water，it significantly affects the hydrodynamic conditions through changes of both the flow velocity fields and the sediment transport process. Furthermore， the presence of a bridge pier can further change the flow conditions. For example， a pier can initiate the formation of an ice jam and at the same time increase the possibility of ice jam flooding［1-4］. Meanwhile， a bridge pier can significantly affect the flow velocity field and result in a local scour around the bridge pier or the abutment［5］. The formation of an ice jam in the vicinity of a bridge pier can also potentially harm the safety of the bridge infrastructure， such as by the local scour around the bridge pier or by the bridge pier. Both the forces and the shear stress acting on the bridge piers（caused by the flowing water and the ice jam） can also be increased. Consequently， comparing to the flow conditions without the bridge pier， the presence of a bridge pier changes the flow field and the forces acting on the ice jam in the vicinity of the bridge pier. Hence， the stability of the ice jam will be affected. This paper investigates the characteristics of the ice jam around a bridge pier. Stability analysis is conducted for the prediction of the formation of an ice jam.

To study the ice force on a structure， either experimental approaches［6，7］， or stress analyses or numerical simulations［3］were used. Recently， the local scour around bridge piers under ice-covered conditions was studied［8］. The experimental approach is based on flume experiments to study the ice jam around bridge piers. Urroz et al.［9］conducted one small scale flume experiments to investigate the ice cube conveyance around bridge piers. It is shown that the location of the pier can affect the ice cube conveyance in sinuous channels significantly. They suggested that the deleterious effects on the ice conveyance in sinuous rivers with bridges crossing can be reduced by installing bri-dges at the apex of channel bends. In the past decades，numerical simulations for the river ice process were also significantly improved due to the advances in computer technologies. Xiong and Xu［10］presented one numerical simulation for the interaction process between the river ice and the bridge pier. They indicated that the river ice increases the lateral constraint stiffness of the bridge piers. They suggested that the proper contact stress value should be around 0.88 MPa，much less than 2.88 MPa， as indicated in the CAS guideline［11］. The stress analysis is another approach used to study the ice jam around bridge piers. Yu et al.［12］analyzed the floating ice cubes on the Huma River based on field observations. The stress acting on the bridge pier was also calculated. According to Beltaos et al.［4］， if the flow drag force together with the gravity force is larger than the resistant force provided by the pier， the chance for the formation of an ice jam around pier is small. In the present paper， the interactions between the bridge piers and the ice jam around the piers are studied experimentally， by numerical simulations and stress analyses. In the interactions between the ice jam and the bridge pier， the ice jam is treated as the accumulation of a number of individual ice cubes （or ice jam elements） under the ice cover. For the stress analyses under the equilibrium state， a governing equation for describing the stability of the ice jam is developed. The developed equation is then applied by using the field data to assess the stability of the ice jam around the bridge pier. Calculated results agree well with the field observations.

1. Internal stress of ice jam and model

A major consequence of the ice-cover formation in many rivers is the associated jamming， particularly，during the periods of fall freeze-up or spring breakup. In fact， the ice jamming is one of the most conspicuous and momentous ice-related phenomena. Ice jams are formed when the ice transported by the current is arrested by obstacles such as the stationary ice cover， or congested， say， due to a local reduction of the ice-transport capacity［13-15］. The ice jam is normally formed by accumulation of vast amount of frazil particles and ice blocks. Due to the large thickness and the high hydraulic resistance of the aggregate ice relative to the sheet ice， the ice jams tend to disturb the riverbed， can lead to a high water stage and many other problems［16］. The formation and the development of the ice jam are related with the complicated hydraulic conditions， the thermal regime and the boundary conditions in natural rivers. Also， an ice jam evolves during its presence in the river. Therefore， it is extremely difficult to precisely describe the ice jam process by using mathematical equations.

The equilibrium state of an ice jam in the river is the result of the joint actions of many forces. Since an ice jam consists of vast amount of individual ice jam elements， an individual ice jam element is selected for the stress analysis. Forces acting on the ice jam element include the drag force， the gravity force and the buoyant force as well as the resistant force from the pier.

Fig.1 Stress analysis of a unit element of ice jam

1.1 Stress analysis of the ice jam section from the ice jam toe to the front surface of pier

The external stress of the ice jam from the ice jam toe to the front surface of the pier is not affected by the bridge pier， but is affected by the drag force on the ice jam bottom surface caused by the flowing water （τi）， the gravity force component in the flow direction （siρgtSw）， the supporting force from the river bank and pier （k0λc）as well as the cohesive force （τc）. Following the analysis procedure of Kenedy （1958）， the stress analysis of an ice jam element is carried out as shown in Fig.1.

Hence， the force analysis for an ice jam element in equilibrium leads to the following equation：

where siis the specific gravity of ice，tis the thickness of the ice jam，ρis the mass density of water， Swis the hydraulic slope，k0is the transverse thrust coefficient，g is the gravity acceleration，τiis the drag force on the ice jam bottom surface，B is the ice jam width， which is equal to the river width in this case，F is the internal force acting on a unit length of the ice jam，λcis the internal friction coefficient， τcis the internal cohesive force of the ice jam.

Here， it is assumed that the hydraulic pressure force at the ice jam toe is f1. Equation （1） is integrated to obtain，which is also the modified Kennedy Equation from Pariset et al. （1966）.

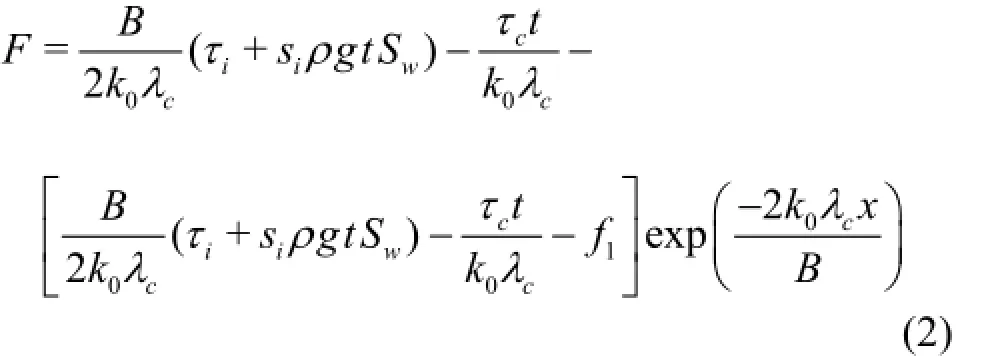
Fig.2 Stress analysis of a unit element of ice jam affected by pier

1.2 Stress analysis of ice jam section from the front surface of pier to the rear surface of pier

Because the presence of the bridge pier， the stresses acting on the ice jam section are changed significantly from the front surface of the pier to the rear surface of the pier in the flow direction. Comparing to the flow condition without the pier， the forces acting on the ice jam in front of the pier include the drag force on the ice jam bottom caused by the flowing water，the gravity force component in the flow direction， the supporting force caused by the river bank and the pier，the friction forces between the pier and the ice jam as well as the cohesive force， as shown in Fig.2.

Therefore， according to the analysis of the ice jam in equilibrium， the forces acting on an ice jam element can be expressed as

wheren is the number of bridge piers，λpis the internal friction coefficient between the ice jam and the bridge pier［17］，τpis the cohesive force between the ice jam and the bridge pier.

According to the American Association of State Highway and Transportation Officials［18］， the forces acting on the bridge pier by the ice can be calculated as follows：

α is the angle between the pier surface and the ice cover， which should be larger than 15o，pis the effective pressure，wis the interaction area on the front pier surface with ice.

Regarding the pressure on the bridge piers caused by the ice jam， AASHTO （2004） suggests that the range should be between 0.96×10-3MPa and 9.6× 10-3MPa， while the Canadian Highway Bridge Design Code （CSA， 2004） suggests a range from 5× 10-3MPa to 10-2MPa.

If the location of the front surface of the pier is x=x0， Eq.（2） can be used to determine the force per unit width acting on the front face of the bridge pier

Meanwhile， Eq.（3） is integrated， with the initial conditions of x=x0，F=F2， then we have

It is clear that 0≤x-x0≤l， in which，lis the length （or thickness） of the pier in the flow direction（in this case，l is equal to the diameter of the pier）. From the expression ofF ， it can be found that， with the presence of the bridge pier， the supporting force due to the bridge pier is increased while the internal force of the ice jam is decreased. If x-x0=l， the internal forces of the ice jam at the rear surface of the bridge pier can be obtained as

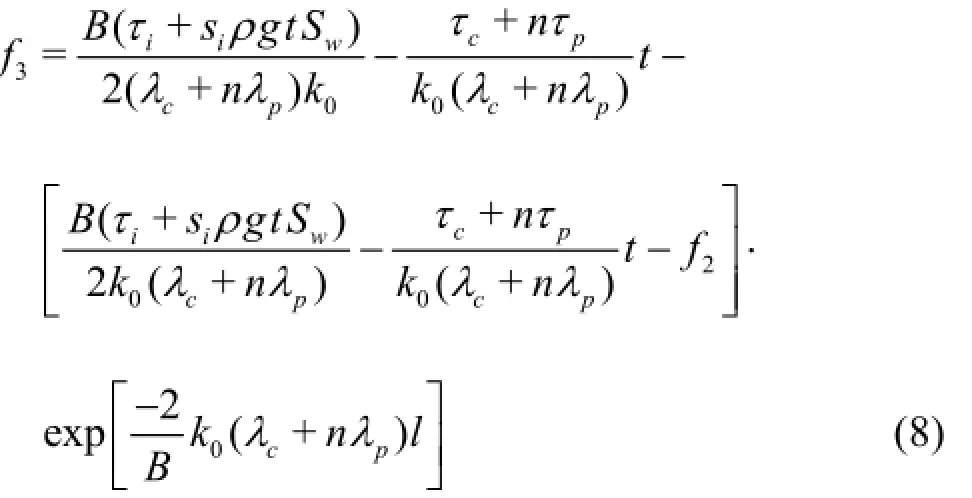
1.3 The stress analysis of ice jam section from the rear surface of pier to the tail section of ice jam

The stress analysis of the ice jam section from the rear surface of the bridge pier to the tail section of the ice jam is nearly similar to the analysis for the ice jam section from the ice jam toe to the front surface of the pier （as mentioned in Section 2.1）. However， as the initial condition， the supporting force on the ice jam provided by the pier will be changed. As shown in Fig.1， from the forces acting on an ice jam element，we can obtain

Integrating the above equation with the initial conditions of x=x0+l，F=F3， the following equation can be obtained

As pointed out by Beltaos， comparing to the internal friction forces on the ice jam， the cohesive forces can be neglected. Therefore，τc=0，τp=0. By analyzing Eqs.（2）， （7） and （10）， the following conclusions can be drawn.

（1） If the ice jam is in an equilibrium state before reaching the bridge pier， which also means thatx→∞in Eq.（2），Fcan reach its extreme value and can be expressed as

The internal force of the ice jamFas shown by Eq.（11）， which was also obtained by Pariset et al.（1966）， is for an equilibrium ice jam before reaching the bridge pier （namely， when the bridge pier has no impacts on the ice jam）. The force acting on a unit width of the front surface of the bridge pier can be expressed as

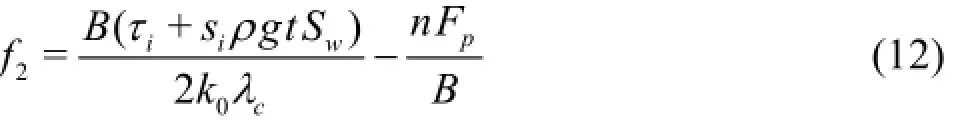
（2） The unit internal force at the rear surface of the bridge pier can be described as：

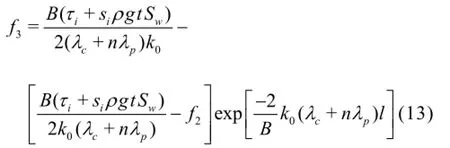
Assuming that

Eq.（13） is turned into

By substituting Eq.（14） into Eq.（12）， we have

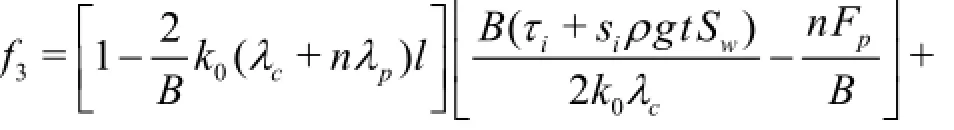
Pariset et al. （1966） treated the maximum strength of the ice jam as the passive pressure of movable particles， which means that：

It is obvious that if the external forces acting on the ice jam are smaller than the internal forces， the ice jam could stay in a stable condition. Hence，

where the equilibrium in the extreme state can be reached if F=Kγt2. The ice jam reaches the maxipemum strength under this condition.Kpis the passive earth pressure coefficient，γeis the specific gravity of ice cubes， which is equal to

Table 1 Parameters used in the present study

Table 2 Ice jam and hydraulic conditions at the Utsutsu River bridge and Shokotsu River bridge in Japan

At the location of the rear surface of the bridge pier， the equilibrium state of the ice jam can be reached under the following condition.

Equation （18） is the governing equation for describing whether or not an ice jam around bridge piers is stable.

2. Validation of governing equation and analysis

Due to the lack of field observations， the field data from Beltaos et al.［4］and Shen et al.［19］are used for the validation of the governing equation for determining if the ice jam is stable. In the present study， the values of the following parameters are used， as shown in Table 1.pJis the ice cube pore rate，f0is the water underside friction coefficient，fiis the friction coefficient of the ice cubes.

2.1 Case 1： Bridge over the Saint John River between Clair/New Brunswick， and Fort Kent/Maine

Based on the field observations， for the bridge over the Saint John River between Clair， New Brunswick/Canada， and Fort Kent， Maine/USA， Beltaos et al.［4］suggested that τi+siρgtSw=15 Pa， B≈190 m，t =0.5 m，n=2. According to AASHTO［18］， the calculated force is Fp=11040 N. Equation （18） gives：

Sincef3＞Kpγet2， it is indicated that the ice jam cannot be formed. According to Beltaos et al.［2］， based on the long-term observations from 1933 to 2004， there had never been ice jams observed at this location because of the bridge piers. Thus， the governing Eq.（18） for prediction of the ice jam formation around bridge piers at this location is valid.

2.2 Case 2： The Utsutsu River Bridge and Shokotsu River Bridge in Japan

Shen et al.［19］collected a great number of data for ice jams and flow conditions at the Shokotsu River Bridge and the Utsutsu River Bridge in Japan， as shown in Table 2. Using Eq.（18）， the stability analysis for ice jams at these 2 locations is conducted. As shown in Figure 3， the point of intersection of the line f and the curveKγt2in Figure 3 represents the3peequilibrium state of the ice jam under the critical condition. Under the condition of f＞Kγt2， the ice jam3peis in an unstable state. It can also be noted from Figure 3 that， with the increase of the ice cube thickness， the value of f3decreases correspondingly， which can be attributed to the increase of the supporting force provided by the bridge piers. Meanwhile， the extreme ice cube forces increase evidently with the increase of the ice cube thickness. When the value exceeds the value of the intersection point of Kγt2and f）， the valuepe3of f keeps smaller thanKγt2， in other words， the3peice cube stays in a stable state.

From Fig.3 and Table 2， according to the governing equation for assessing the stability of an ice jam， one can see that f＞Kγt2under all flow conditions.3peIt means that the ice jam cannot be formed in the vicinity of both the Utsutsu River Bridge and the Shokotsu River Bridge. Additionally， the ice coverage around the Utsutsu River Bridge is only 10%. While the ice coverage in the vicinity of the Shokotsu River Bridge is reduced from 100% （1995-02-06） to 10%（1995-03-16）. It suggests that the ice cover around these two bridges are all under an unstable state. Thepredicted results show a good agreement with the field observations at these 2 bridge locations.

Fig.3 Stability analysis of ice jams at Utsutsu River and Shokotsu River bridges

3. Conlcusion

The presence of bridge piers in rivers complicate the flow field as well as the forces acting on the river ice， and the possibility of the formation of ice jams in the vicinity of bridge piers is increased. In the present study， the stress analyses of the ice jam section in the vicinity of the bridge pier （both upstream section and downstream section） are carried out. The governing equation is developed to assess the stability of an ice jam around bridge piers. Using field data collected at the Utsutsu River Bridge and the Shokotsu River Bridge， the governing equation for assessing the stability of an ice jam in the vicinity of bridge piers is validated. One can see that the predictions agree well with the field data.

［1］ BELTAOS S. Progress in the study and management of river ice jams［J］. Cold Regions Science and Technology， 2008， 51（1）： 2-19.

［2］ BELTAOS S. River ice breakup processes： Recent advances and future directions［J］. Canadian Journal of Civil Engineering， 2007， 34（6）： 703-716.

［3］ BELTAOS S.， MILLER L. and BURRELL B. C. et al. Hydraulic effects of ice breakup on bridges［J］. Canadian Journal of Civil Engineering， 2007， 34（4）：539-548.

［4］ BELTAOS S.， MILLER L. and BURRELL B. C. et al.Formation of breakup ice jams at bridges［J］. Journal of Hydraulic Engineering， ASCE， 2006， 132（11）： 1229-1236.

［5］ SUI J.， AFZALIMEHR H. and SAMANI A. K. et al. Clear-water scour around semi-elliptical abutments with armored beds［J］. International Journal of Sediment Research， 2010， 25（3）： 233-245.

［6］ BROWN T. G. Analysis of ice event loads derived from structural response［J］. Cold Regions Science and Technology， 2007， 47（3）： 224-232.

［7］ SODHI D. S.， HAEHNEL R. B. Crushing ice forces on structures［J］. Journal of Cold Regions Engineering，2003， 17（4）：153-170.

［8］ WU P.， HIRSHFIELD Faye and SUI J. Impacts of ice cover on local scour around semi-circular bridge abutment［J］. Journal of Hydrodynamics， 2014， 26（1）： 10-18.

［9］ URROZ G. E.，SCHAEFER J. and ETTEMA R. Bridge-pier location and ice conveyance in curved channels［J］. Journal of Cold Regions Engineering， 1994，8（2）： 66-72.

［10］ XIONG F.， XU G. Numerical investigation of river icebridge pier interaction［C］. Proceedings of the Structures Congress. Austin Texas， USA， 2009， 48-57.

［11］ CANADIAN STANDARDS ASSOCIATION. Canadian highway bridge design code［S］. Toronto， Ontario，Canada： Canadian Standards Association， 2006.

［12］ YU T.， LEI J. and LI C. et al. Compressive strength of floating ice and calculation of ice force on bridge piers during ice collision［C］. Cold Regions Engineering 2009： Cold Regions Impacts on Research， Design，and Construction. 2009， 609-617.

［13］ MORSE B.， HICKS F. Advances in river ice hydrology 1999-2003［J］. Hydrological Processes， 2005， 19（1）：247-264.

［14］ BELTAOS S. Advances in river ice hydrology［J］. Hydrological Processes， 2000， 14（9）： 1613-1625.

［15］ SUI J.， KARNEY B. W. and SUN Z. et al. Field investigation of frazil jam evolution： A case study［J］. Journal of Hydraulic Engineering， ASCE， 2002， 128（8）：781-787.

［16］ SUI J.， WANG D. and KARNEY B. W. Suspended sediment concentration and deformation of riverbed in a frazil jammed reach［J］. Canadian Journal of Civil Engineering， 2000， 27（6）： 1120-1129.

［17］ BARKER A.， SAYED M. and TIMCO G. Numerical simulation of ice interaction with a wide cylindrical pier［C］. Cold Regions Engineering Cold Regions Impacts on Transportation and Infrastructure， Proceedings of the Eleventh International Conference. Anchorage， AK， USA， 2014， 617-628.

［18］ AMERICAN ASSOCIATION OF STATE HIGHWAY，TRANSPORTATION OFFICIALS. Standard specifications for highway bridges［S］. AASHTO， 2004.

［19］ SHEN H. T.， LIU L. Shokotsu River ice jam formation［J］. Cold Regions Science and Technology， 2003，37（3）： 35-49.

* Project supported by the National Natural Science Foundation of China （Grant Nos. 51379054， 50979021）.

Biography： WANG Jun （1962-）， Male， Ph. D.， Professor

SUI Jueyi， E-mail： jueyi.sui@unbc.ca