Experimental investigation of motion responses of tunnel element immerging by moored barge*

ZUO Wei-guang （左卫广）， WANG Yong-xue （王永学）State Key Laboratory of Coastal and Offshore Engineering， Dalian University of Technology， Dalian 116024，China， E-mail：weiguangzuo2004@163.com

Experimental investigation of motion responses of tunnel element immerging by moored barge*

ZUO Wei-guang （左卫广）， WANG Yong-xue （王永学）
State Key Laboratory of Coastal and Offshore Engineering， Dalian University of Technology， Dalian 116024，China， E-mail：weiguangzuo2004@163.com

（Received May 28， 2014， Revised December 10， 2014）

In this paper， the barge effect on the motion responses of the tunnel element immerging by the moored barge under waves is investigated experimentally. Both the motion responses of the tunnel element and the moored barge in the experiment are simultaneously acquired by the Untouched 6-D Measurement System. The results show that the sway motion responses of the tunnel element immerging by the moored barge are different from those without the barge. For the system of the tunnel element and the moored barge， the moored barge has two motion components in the sway direction. The high frequency motion of the moored barge has little effect on the high frequency motion of the tunnel element with moored barge. However， the low frequency motion of the moored barge has a significant effect on the sway motion of the tunnel element. The motion responses of the tunnel element and the barge in the heave and roll directions are mainly the high frequency motion.

tunnel element， moored barge， motion responses， low frequency motion， maximum offset

Introduction0F

The immersing method is an innovative technique for the subsea tunnel construction. The process consists of dredging a trench on the river or sea bottom， transporting the prefabricated tunnel elements，immersing the elements one by one to the trench， connecting the elements， backfilling the trench and installing equipments inside the tunnel［1-3］. Several key engineering techniques are involved， such as the transporting and the immersing， the underwater linking，the water proofing and the protection against earthquake［4-7］. Nowadays， the immersion of tunnel elements plays a more and more important role in the construction， and has a great bearing on the safety of the construction. However， it was not well studied， compared with other technical issues related to the immersing method［8-12］.

There are several immersing methods， such as the pontoon immersing， the platform immersing， the lift immersing and the barge immersing. Because the barge immersing enjoys advantages of great carrying capacity of the tunnel elements and convenient construction， it is used in more and more projects. When the immersion of tunnel elements is done by the moored barge， the motion of the tunnel elements is caused by the wave and barge motions. Thus， it is necessary to study the dynamic characteristics of the immersed tunnel elements in the wave and with the barge.

The fluid force and the cable tension in the immersion of the tunnel elements were studied by Zhan［13，14］， in which the velocity， the wave height and the ballast water were used to analyze their influence on the immersion stability of the tunnel elements. Jensen et al.［15］established the wave model in the construction area， analyzed the motion characteristics of the tunnel immersion and studied the influence of the offshore wave condition on the immersion of the tunnel elements. Zhou［16］obtained experiment results of the cable tension and computed the frequency responses of the tunnel elements in the initial state of immersion but without details of the motion responses ofthe tunnel elements. Chen et al.［17，18］carried out experiments on the immersion of the tunnel elements in several immersing depths and the test results were consistent with those of the numerical model. However， the barge effects on the motion responses of the tunnel element were not duly considered in most cases.

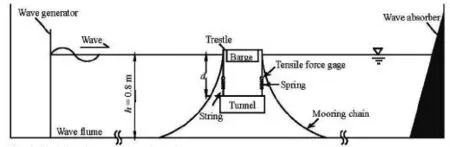
Fig.1 Sketch of the experimental set-up

The present study investigates experimentally the motion dynamic characteristics of tunnel elements with consideration of the effect of the barge motion. The motion responses of the tunnel elements in waves and with a moored barge in the tunnel element-moored barge system are analyzed and discussed.

1. Experiment set-up

The experiment of tunnel elements immerging by the moored barge is conducted in the marine environmental channel in the State Key Laboratory of Coastal and Offshore Engineering， Dalian University of Technology. The wave channel is 50 m in length， 3 m in width and 1 m in height. The sketch of the experimental set-up is shown in Fig.1.

The prototype tunnel element of 100.0 m in length， 15.0 m in width and 10.0 m in height is used as the reference in the experimental design and the characteristic values of the prototype tunnel element and barge are collected from the available construction projects. In the model test design， the geometric scale of 1：50 is used and the model parameters of the tunnel element， the barge and the waves are determined based on the geometry and the gravity similarity criterion. The parameters of the mooring system are determined based on the length， mass and elasticity similarities and the parameters of the suspension cables are determined based on the cable tension-deformation curve， which is calculated by the Wilson formula from the field data.

The tunnel element model with hollow cuboids sealed at each ends is made of acrylic plate and concrete. The size of the tunnel model is 2.0 m in length，0.3 m in width and 0.2 m in height. The weight of the tunnel element model in air and in water is 1 200.5 N and 1 176.0 N， respectively. The negative buoyancy is 2.08% of the buoyancy force of the tunnel element.

The single barge model is made of acrylic cuboids， and is of 1.0 m in length， 0.16 m in width and 0.16 m in height. The barge weight is 156.8 N and the draught is 0.10 m. The barge model is moored by four steel chains with springs （elasticity coefficientof 1.34 N/mm）. A pair of chains are installed on the seaside of the barge and another pair of chains are installed on the shore side of the barge.

The four steel wires with springs are used as the suspension cables. One end of the suspension cable is connected to the barge and another is connected to the tunnel model as shown in Fig.1. Three kinds of springs with different elasticity coefficients， corresponding to three immersing depths， are used in these experiments. The appropriate springs are chosen according to the cable properties and the reasonable scales of model tests are listed in Table 1.

Table 1 Relation between the immersing depth and spring elasticity coefficient

Table 2 Experiment conditions

In this test， regular waves are considered. The water depth， the wave height， the wave period and the immersing depth are shown in Table 2. The immersing depth is the distance from the water surface to the top surface of the tunnel element.

Fig.2 Untouched 6-D measurement system

The motions of the tunnel element and the barge in sway， heave and roll directions are acquired by the Untouched 6-D Measurement System， which is composed of optical， mechanical， electronic circuits and other hardware control systems and a graphical analysis software system. The tunnel element， the moored barge and the Untouched 6-D Measurement System are as shown in Fig.2. Three light-emitting diodes are placed in the front face of the tunnel element and another three light-emitting diodes in the front face of the moored barge. The Untouched 6-D Measurement System is used to obtain the location and the metrical values of the target through the method based on the visual measuring principle and the digital image processing technology. Besides， the Untouched 6-D Measurement System has the advantages of noninterference，high accuracy and easy operation. It is calibrated that the error of the motion measurement system can be controlled within 0.3% in surge， sway， heave directions， and 1.2% in roll， pitch， yaw directions.

2. Results and Discussions

2.1 Barge effect on the motion responses of tunnel element

In order to analyze the effect of the moored barge on the motion responses of the tunnel element immerging by moored barge in waves， the motion responses of the tunnel element without barge in waves are also obtained in the physical model tests.

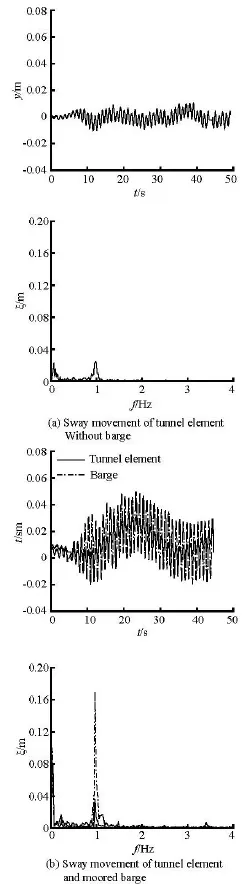
Fig.3 Time series and spectral analysis of sway movements of the tunnel element without and with moored barge （d= 0.30 m，H =0.05 m，T =1.0s）

Firstly， the typical time series of the sway（y），heave（z ）and roll（θ）movements of the tunnel element without and with moored barge are compared. Figure 3 shows the typical time series and the spectral analysis of sway movements of the tunnel element without and with moored barge for d =0.30 m，H= 0.05 m and T=1.0s. The positive sway， heave and roll movements are corresponding to the horizontal displacement along the wave， the upward direction and the anticlockwise rotation， respectively. The solid line is the sway motion of the tunnel element and the dashed line is the sway motion of the moored barge.

It is seen from Fig.3 that the effect of the moored barge on the sway movements of the tunnel element is significant compared with the sway movements of the tunnel element without barge. The time series of the sway movements of the tunnel element without barge are mainly a high frequency movement， while the sway movements of the tunnel element with moored barge are a combination of a high frequency movement and a low frequency movement.

Fig.4 Time series of heave movements of the tunnel element without and with moored barge （d =0.30 m，H= 0.05 m，T =1.0s）

The spectral analysis of the sway movements of the tunnel element and the moored barge （Fig.3（b））shows that the high frequency value （1.0 Hz） of the tunnel element with barge is the same as the wave frequency， while the low frequency value （0.045 Hz） of the tunnel element with barge is the same as the low frequency value of the moored barge. It can be figured out that the high frequency motion （1.0 Hz） and the low frequency motion （0.045 Hz） of the tunnel element with moored barge are related to the wave excitation and the low frequency motion of the moored barge， respectively.

For the system of the tunnel element and the moored barge， the moored barge has two motion components in the sway direction due to the wave action. The high frequency motion component is with the same frequency as the wave frequency and the low frequency motion is related to the slow drift motion of the moored barge. From Fig.3（b）， the amplitudes of the high frequency motion of the tunnel element without and with moored barge in the sway direction are 5.63×10-3m and 5.10×10-3m. It means that the high frequency motion of the moored barge has little effect on the high frequency motion of the tunnel element with moored barge， although the amplitude of the high frequency motion of the moored barge is fairly large. However， both the low frequency motions of the tunnel element and the moored barge are almost the same. That is， the low frequency motion of the moored barge has a significant effect on the sway motion of the tunnel element.

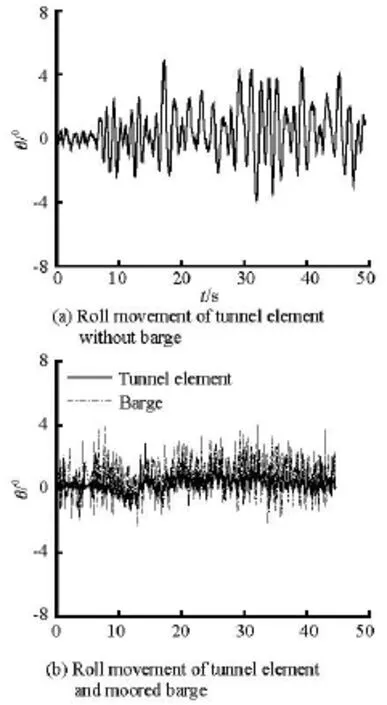
Fig 5 Time series of roll movements of the tunnel element without and with moored barge （d =0.30 m，H =0.05 m，T =1.0s）

Fig.6 High frequency motion amplitudes of the tunnel element and moored barge under different wave conditions （d=0.30 m）

The maximum offset of the tunnel element is defined as the maximum sway displacement of the tunnel element away from its original balance position，and it is a significant parameter for the sinking control and the orientation of the tunnel element during the process of construction. It is shown from Fig.3（b） that the maximum offsets of the tunnel element without and with moored barge are 8.59×10-3m and 2.17× 10-4m， respectively and the maximum offset of the tunnel element is mainly affected by the low frequency motion of the moored barge.

Figures 4 and 5 show typical time series of the heave and roll movements of the tunnel element without and with moored barge for d =0.30 m，H= 0.05 m and T=1.0s. The heave and roll motions of the tunnel element and the moored barge in the tunnel element-moored barge system are mainly the high frequency motions related to the wave excitation. That is， the tunnel element and the moored barge oscillate at the wave frequency. Compared with the heave and roll motions of the tunnel element without barge， the heave and roll motions of the tunnel element with moored barge are reduced in this sample case. It might be the reason why the heave and roll motions of the moored barge are restricted by the mooring chains and a larger phase difference is generated between the tunnel element and the moored barge.

From the typical time series of the motion responses of both the tunnel element and the moored barge，it is seen that the motion responses of the tunnel element in the sway direction come mainly from the low frequency motion of the moored barge， and the motion responses of the tunnel element in the heave and roll directions come mainly from the high frequency motion. Therefore， the non-dimensional amplitudes of the high frequency motion of the tunnel element and the moored barge are mainly studied in the sway， heave and roll directions under different wave conditions，and the non-dimensional amplitudes of the low frequency motion of the tunnel element and the moored barge are mainly studied in the sway directions.

Figure 6 shows the non-dimensional amplitudes of the high frequency motion of the tunnel element and the moored barge in the sway， heave and roll directions at the immerging depth d=0.30 m. In the figure， the solid line denotes the motion amplitude of the tunnel element immerging by the moored barge in the moored barge-tunnel element system， the inverted solid triangle symbols denote the motion amplitudes of the moored barge， and the solid triangle symbols denote the motion amplitudes of the tunnel element without barge.

It is again seen that the amplitudes of the high frequency sway motion of the tunnel element immerging by the moored barge see no significant differences as compared with those without the barge motion under different wave conditions， although the amplitudes of the high frequency sway motion of the moored barge are fairly large. However， the moored barge has a certain effect on the heave and roll motions of the tunnel element， and the amplitudes of the heave and roll motion of the tunnel element with barge are sma-ller than those without barge. With the increase of the wave height and the wave period， the amplitudes of the high frequency heave and roll motion of the tunnel element immerging by moored barge are increased.

Fig.7 Amplitudes of low frequency sway motion of the tunnel element and the moored barge under different wave conditions （d=0.30 m）

The non-dimensional amplitudes of the low frequency sway motion of the tunnel element and the moored barge under different wave conditions are shown in Fig.7. The low frequency motion amplitudes of the tunnel element with moored barge （solid line）are nearly same as the low frequency motion amplitudes of the barge with the tunnel element （inverted solid triangle symbols） under different wave conditions. For a small wave period， the amplitudes of the low frequency motion of the tunnel element with moored barge （solid line） are larger than those without barge（solid triangle symbols）. It is shown that the low frequency motion of the barge in the sway direction has a significant effect on the amplitudes of the low frequency sway motion of the tunnel element. However， with the increases of the wave periodT ， the moored barge effect on the amplitudes of the low frequency motion of the tunnel element is reduced.

Figure 8 shows the non-dimensional maximum offsets （ymo）of the tunnel element and the moored barge in the sway direction. From the figure， it is shown that the maximum offsets of the moored barge（inverted solid triangle symbols） are the largest because of the large drift motion of the moored barge in a regular wave. The non-dimensional maximum offsets of the tunnel element with consideration of the barge motion （solid line） are much larger than those ignoring the barge motion （solid triangle symbols）. It again indicates that the low frequency sway motion of a moored barge has a significant effect on the maximum offset of the tunnel element in the moored barge-tunnel element system. The maximum offset of the tunnel element in the moored barge-tunnel element system is large for a small wave periodT at a certain wave heightH and immerging depthd. And the maximum offsets of the tunnel element without and with barge are reduced with the increase of the wave periodT.

Fig 8 Maximum offsets of the tunnel element and the moored barge under different wave conditions （d=0.30 m）

It is seen from Fig.8 that the non-dimensional maximum offsets of the tunnel element with barge are 0.80（H =0.03m）and 1.22（H =0.05 m）at T= 0.70 s， which is four times larger than those without barge. The amplitudes of the low frequency motion of the tunnel element with moored barge make a main contribution to the maximum offset for a small wave period， because the amplitudes of the high frequency motion of the tunnel element with moored barge are very small. The non-dimensional maximum offsets of the tunnel element with barge are 0.36（H=0.03m） and 0.63（H =0.05 m）at T =1.0s， which is nearlytwo times larger than those without barge. The amplitudes of the low frequency motion of the tunnel element with moored barge are approximately 50% of the maximum offset for a small wave period.

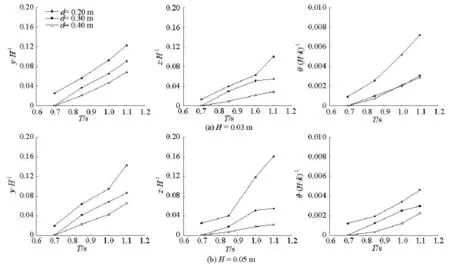
Fig.9 Amplitudes of high frequency motion of the tunnel element with moored barge under different immerging depths

Fig.10 Amplitudes of low frequency motion of the tunnel element with moored barge in sway direction under different immerging depths

2.2 Motion responses of the tunnel element with barge under different immerging depths

The experiments are conducted for different immerging depths to study the effects of the immerging depths on the motion responses of the tunnel element with moored barge. Figure 9 shows the amplitudes of the non-dimensional high frequency motion of the tunnel element and the moored barge versus the wave periods under the immerging depths of 0.20 m， 0.30 m and 0.40 m. It is seen from the figure that the amplitudes of the sway， heave and roll motions of the tunnel element with barge increase with the increase of the wave period and height. With the increase of the immersing depth， the amplitudes of the high frequency motion of the tunnel element with barge are reduced， because the wave effect on the tunnel element is weakened with the increase of the immersing depth.

The non-dimensional amplitudes of the low frequency motion of the tunnel element with barge in the sway direction versus the wave periods under different immerging depths are shown in Fig.10.

With the increase ofT ， the amplitudes of the low frequency motion of the tunnel element with moored barge in the sway direction decrease at a certain immerging depth. The amplitudes of the low frequency motion with barge in the sway direction are the largest in the case of d=0.20 m. And the amplitudes of the low frequency motion in the sway direction for d =0.40 mare little larger than those for d =0.30 mwithin the test range.

3. Conclusions

Based on the experimental investigation on the motion responses of the tunnel element under immersion with moored barge， the conclusions can be obtained as follows：

（1） The moored barge has a significant effect on the sway motion of the tunnel element with barge immerging. The sway motion composes of a high frequency motion caused by waves and a low frequency motion caused by the drift motion of the moored barge. The amplitudes of the high frequency motion of the tunnel element with and without barge see no obvious difference， and the amplitudes of the low frequency motion and the maximum offsets of the tunnel element are relatively larger due to the moored barge effect.

（2） The heave and roll motions of the tunnel element and the moored barge in the tunnel elementmoored barge system are mainly the high frequency motions related to the wave excitation. The moored barge could reduce the amplitudes of the heave and roll motion of the tunnel element， depending on the moored condition.

（3） The immersing depth has a certain effect on the motions of the tunnel element with barge. With the increase of the immersing depth， the amplitudes of the high frequency motion of the tunnel element with barge are reduced.

［1］ INGERSLEV C. Immersed and floating tunnels［J］. Procedia Engineering， 2010， 4（6）： 51-59.

［2］ AONO T.， SUMIDA K. and FUJIWARA R. et al. Rapid stabilization of the immersed tunnel element［C］. Proceedings of the Coastal Structures 2003 Conference. Portland， Oregon， USA， 2003， 394-404.

［3］ KASPER T.， STEENFELT J. S. and PEDERSEN L. M. et al. Stability of and immersed tunnel in offshore conditions under deep water wave impact［J］. Coastal Engi neering， 2008， 55（9）： 753-760.

［4］ FALTINSEN O. M. Hydrodynamics of marine and offshore structures［J］. Journal of Hydrodynamics， 2014，26（6）： 835-847.

［5］ ANASTASOPOULOS I.， GEROLYMOS N. and DROSOS V. et al. Nonlinear response of deep immersed tunnel to strong seismic shaking［J］. American Society of Civil Engineers， 2014， 133（9）： 1067-1090.

［6］ NOROUZI H. R.， TAHMASEBPOOR M. and ZARGHAMI R. et al. Multi-scale analysis of flow structures in fluidized beds with immersed tubes［J］. Particuology，2015， 21： 99-106.

［7］ KIYOMIYA O. Civil engineering field： Steel concrete sandwich composite member （Immersed tunnel element）［J］. Concrete Journal， 2014， 52（1）： 44-49.

［8］ ZHAO Zhan-guang， HUANG Zhou-yi. Discussion on several techniques of immersed tunnel construction［J］. Modern Tunnelling Technology， 2007， 44（4）： 5-8（in Chinese）.

［9］ INGERSLEY L. C. F. Considerations and strategies behind the design and construction requirements of the istanbul strait immersed tunnel［J］. Tunnelling and Underground Space Technology， 2005， 20（6）： 604-608.

［10］ HAKKAART Ch. J. A. Transport of tunnel elements from Baltimore to Boston， over the Atlantic Ocean［J］. Tunnelling and Underground Space Technology，1996， 11（4）： 479-483.

［11］ DING J. H.， JIN X. L. and GUO Y. Z. et al. Numerical simulation for large-scale seismic response analysis of immersed tunnel［J］. Engineering Structures， 2006，28（10）： 1367-1377.

［12］ ANASTASOPOULOS I.， GEROLYMOS N. and DROSOS V. et al. Nonlinear response of deep immersed tunnel to strong seismic shaking［J］. Journal of Geotechnical and Geoenvironmental Engineering，2007， 133（9）： 1067-1090.

［13］ ZHAN De-xin， WANG Xing-quan. Experiments of hydrodynamics and stability of immersed tube tunnel on transportation and immersing［J］. Journal of Hydrodynamics， 2001， 13（2）： 121-126.

［14］ ZHAN De-xin， ZHANG Le-wen and ZHAO Cheng-bi et al. Numerical simulation and visualization of immersed tube tunnel maneuvering and immersing［J］. Journal of Wuhan University of Technology （Transportation Science and Engineering）， 2001， 25（1）： 16-20（in Chinese）.

［15］ JENSEN O. P.， OLSEN T. H. and KIM C. W. et al. Construction of immersed tunnel in off-shore wave conditions Busan-Geoje project South Korea［J］. Tunnelling and Underground Space Technology， 2006，21（3）： 333.

［16］ ZHOU Yu. Study on the above-water operation of large-scale immersed tube tunnel element［D］. Doctoral Thesis， Shanghai， China： Shanghai Jiao Tong University， 2001（in Chinese）.

［17］ CHEN Z.， WANG Y. and WANG G. et al. Experimental investigation on immersion of tunnel element［C］. 28th International Conference on Ocean， Offshore and Arctic Engineering. Honolulu， Hawaii， USA，2009， 1-8.

［18］ CHEN Zhi-jie， WANG Yong-xue and WANG Guo-yu et al. Time-domain responses of immersing tunnel element under wave actions［J］. Journal of Hydrodynamics， 2009， 21（6）： 739-749.

* Project supported by the National Natural Science Foundation of China （Grant No. 11272079）， the Foundation for Innovative Research Groups of the National Natural Science Foundation of China （Grant No. 51221961）.

Biography： ZUO Wei-guang （1981-）， Male， Ph. D. Candidate

WANG Yong-xue，

E-mail： wangyx @ dlut.edu.cn