基于马尔可夫到达过程的两级可修备件（S-1，S）库存优化模型

陈　童，黎　放，狄　鹏

（海军工程大学管理工程系，武汉430033）

基于马尔可夫到达过程的两级可修备件（S-1，S）库存优化模型

陈童，黎放，狄鹏

（海军工程大学管理工程系，武汉430033）

本文以两级可修备件库存系统为研究对象，采用马尔可夫到达过程（MAP）描述备件需求规律，考虑有限维修设施的情况，假设故障件维修时间、备件运输时间以及采购时间均服从phase-type（PH）分布，建立了一种描述能力更强、解析计算性更好的（S-1，S）库存优化模型，并推导出系统缺货量分布函数；然后通过算例演示了模型的优化效果，验证了模型的正确性和适用性。

（S-1，S）库存策略；两级库存；可修备件；马尔可夫到达过程

1　前言

在军事装备、民用高技术产品等领域，对于具有较高可靠性，并且流通量较低的昂贵可修备件，管理者通常选择多级（S-1，S）库存策略。Sherbrooke[1]最早根据这种库存策略开发了METRIC模型，他选择费用约束下的期望缺货量最小为优化目标，假设各级维修能力无限。Grave[2]针对Sherbrooke研究中设计了一种便于理解的近似计算方法。文献[3，4]则针对METRIC模型无限修理能力的假设，研究了维修台有限情况下的多级可修备件库存模型。付兴方等[5]研究了两级库存系统备件分配优化方法。Lau和Song[6]采用非平稳Poisson过程研究了维修能力有限的两级可修库存系统。这些研究均采用Poisson过程描述部件的失效过程，假设维修时间等服从指数分布，这样的假设具有一定的不合理性[7]。Kim等[8]为了放宽假设条件，进一步假设维修时间服从一般分布，维修台有限；但该研究仍是建立在需求到达是Poisson流的基础上，因此假设条件仍略显严格。

本文针对已有研究假设条件过于严格的情况，提出采用马尔可夫到达过程（MAP）描述备件的需求情况，考虑有限维修设施的情况，假设故障件维修时间、备件运输时间以及采购时间均服从一般分布，采用phase-type（PH）分布进行表示；建立了一个描述能力更强的两级可修备件（S-1，S）库存模型。采用MAP描述需求到达过程时，（S-1，S）策略通常并不是最优策略，这是因为当需求过程比较平稳时，适当增加订货延迟时间是有助于降低成本的。但在军事和工业领域，备件缺货除了对费用的影响，往往还会导致任务失败或增加设备的安全风险，因此采用（S-1，S）策略更加稳妥，也更符合实际情况。

利用MAP和PH分布开展研究具有如下好处。

1）将备件需求过程表示为MAP形式便可以利用“MAP类在[0，+∞）的概率空间上，对平稳点过程类似稠密[9]”这一性质。该性质使得MAP类涵盖了许多常用的点过程[10]，如泊松过程、PH更新过程等；并且实际的备件需求往往具有突发性，而MAP本身结构的特点[11]使它能够很好的描述和分析突发现象。因此，MAP非常适合描述备件的需求发生规律。

2）采用PH分布表示一般分布是因为：任何分布总可以选择一个适当的PH分布把它拟合到任意精确的程度[12]，因此PH分布可以作为许多假设分布的一般表述，采用PH分布描述维修时间等能有效避免指数分布等经典分布的局限性。

2　预备知识

首先介绍PH分布和MAP的有关概念。

定义1[7][0,+∞)上的概率分布函数F(∙)称为PH分布，当且仅当它是一个有限状态马尔科夫过程的吸收时间分布，有分布函数

式（1）中，T为m阶方阵；α=(α1，α2，...，αm)为其瞬态的初始概率向量；e为元素均为1的m阶列向量；(α，T)称为该PH分布的m阶表示。PH分布中的每一个瞬态称为相位。

定义2[11]一个有限不可约马尔可夫链具有状态空间S={1，2，...，m}，设D为该马尔可夫链的无穷小生成元。状态i的逗留时间服从参数为λi的指数分布，在该状态即将结束时，有下列两个事件之一发生：

1）存在一个马尔可夫链，使得从状态i到 j（1≤i，j≤m）的转移中，有一个事件到达的概率为pij(1)；

2）存在一个马尔可夫链，使得从状态i到 j（1≤i，j≤m；i≠j）的转移中，没有事件到达的概率为pij(0)。

可以看到只有通过一次事件到达，才能使得状态i返回到自身。并且有：

D0和D1分别是控制没有事件到达和有单个事件到达的状态转换矩阵，它们均为m阶子随机矩阵，可以给出无穷小生成元D=D0+D1。

然后，定义A(t)为在(0，t]内事件到达的次数；J(t)为在时刻t嵌入马尔可夫链所处的状态，其状态空间为{i:1≤i≤m}。则{A(t)，J(t)}为一个两维马尔可夫过程，其状态空间为{(n，i):n≥0，1≤i≤m}。而{A(t)，J(t)}被称为马尔可夫到达过程。

MAP是半马氏过程的特例，其状态转移概率矩阵为：

设π是无穷小生成元为D的稳态概率向量，则有：πD=0, πe=1。并且πD1e表示在MAP进入稳态后，单位时间内事件到达的期望个数。

下面给出Kronecker乘积的定义，它在后面的模型中被大量使用。

定义3[13]如果 A和B分别为m1×m2和n1×n2的矩阵，它们的 Kronecker乘积 A⊗B则为m1n1×m2n2的矩阵，且：

3　问题描述

本文假设如下。

1）一个中心仓库通常负责N个基地的备件供应和维修，在中心仓库和基地分别存有S0和Si（i=1，...，N）个某型备件，并且在中心仓库和每个基地均有一个维修站。

2）基地i（i=1，...，N）的故障到达是一个MAP，具有m阶表示（E0(i)，E1(i)）。

3）当基地i中出现一个备件需求时，若该基地中仍有库存，则立刻满足该需求。基地i备件需求处理过程示意图见图1。该更换下来的故障件有r的概率可在基地进行维修，否则需交给中心仓库处理。

4）故障件交还中心仓库得同时，基地向中心仓库申领一个备件，若中心仓库有库存则立即下发，否则需要等待维修完成或订货到达；

5）在中心仓库，故障件有p的概率可修，1-p的概率报废；当发生报废时，中心仓库需向生产厂家订购；

6）基地i（i=1，...，N）的维修站维修时间服从PH分布，具有ki阶表示(αi，Ti)；中心仓库维修站维修时间服从PH分布，具有k0阶表示(α0，T0)；所有维修站均采用先到先服务原则；

7）采购时间服从PH分布，具有 kC阶表示(αC，TC)；

图1　基地i备件需求处理过程示意图Fig.1　The disposal process for spare parts demand of base i

8）从中心仓库向各基地的运输时间服从PH分布，具有kiY阶表示(αiY，TiY)；而从基地向中心仓库运送故障件的时间则可以计入中心仓库的维修时间或采购时间中，不单独列出。

9）所有节点均选择（S-1，S）补充策略。

4　系统特性

下面首先对整个系统的备件供应流程进行分析。

4.1备件供应流程

根据假设条件，可以将整个备件供应流程划分为4个部分，如图2所示。

图2　备件供应流程划分示意图Fig.2　The partition of spare parts supply flow

令OPi、DIi和BOi分别表示基地i的工作部件数、维修队长和缺货量；和表示在中心仓库的等待维修队长和采购队列队长，则表示中心仓库不可用件数量；而中心仓库的缺货量为BO0，其中基地i在中心仓库未满足订单的比例为 fi；OH0和OHi分别表示中心仓库和各基地的可用件数量；在运往基地i途中的备件数为TRi。下面研究这些参数之间的关系：

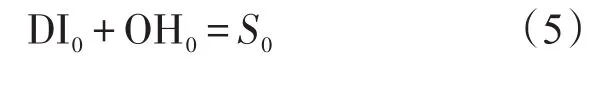
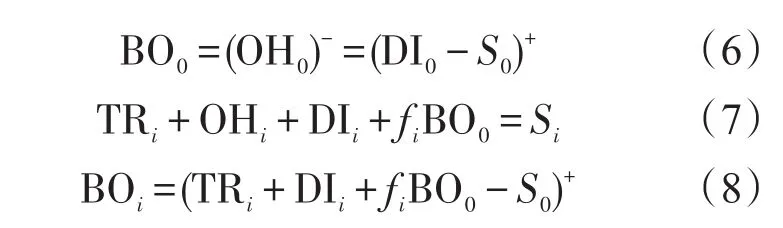
由上述关系式可知，BO0和BOi可以表示为多个随机变量的卷积形式。而又由假设条件可知和TRi均是MAP/PH/1排队系统的队长，则通过研究MAP/PH/1排队系统可知它们所服

从的分布。

4.2MAP/PH/1排队系统

令ψ(t)=(S(t)，I(t)，J(t))，其中S(t)、I(t)和J(t)分别为在时刻t的系统顾客数，顾客到达过程相位和服务台工作相位；另假设服务时间服从k阶PH (a，T)分布。则为连续时间马尔可夫链，其状态空间 Ω可以表示为：Ω=h1⋃h2。其中，h1={(0，i)：1≤i≤m}表示系统内没有顾客；h2={(s，i，j)：1≤s，1≤i≤m，1≤j≤k}表示系统内有s个顾客，其中一个顾客正在接受服务。

通常称S(t)为状态空间的宏状态。对宏状态按字典序排列，可以给出该马尔可夫链的无穷小生成元矩阵：

式（9）中，B00=D0；B01=D1⊗a；B10=D0⊗T0；A0=D1⊗T；A1=D0⊗T+D1⊗T0a；A2=D0⊗T0a。

对维修台工作情况进行分析，发现维修台的状态转移过程亦为一个MAP，其中无穷小生成元矩阵为C=T+T0α；因此，存在一组稳态概率向量πs使得：πsC=0，πse=1。

定理1矩阵A和C均是不可约随机阵，并且矩阵A的稳态概率向量πA=π⊗πs。

证明由A和C的定义已知它们均为不可约随机阵，而：

因此矩阵A的稳态概率向量πA=π⊗πs。定理得证。

由MAP和PH分布性质知，顾客到达率和服务率分别为：λ=πD1e，u=-aT-1e。

Neuts[14，15]给出了求矩阵Q稳态概率向量的一个重要矩阵——率阵R，R是矩阵方程R2A2+RA1+A0=0的最小非负解。

证明根据文献[7]定理2.4知若该马氏链正常返，则必须{} ψ(t)的 R的谱半径 sp(R)＜1，即πAA2＞πAA0，该式正是经典排队系统 μ＞λ条件向矩阵空间的推广。定理得证。

在定理1、定理2的基础上，运用矩阵几何解理论，不难得出：

推论1若 ρ＜1，则矩阵Q的稳态概率向量θ=(θ0，θ1，θ2，...)存在，且θk=θ1Rk-1，k＞1；而 θ0和θ1满足下面的矩阵方程：

并且由下式归一化后可得θ：

θ就是系统在任意时刻的队长分布函数，因此容易给出任意时刻队长的各阶矩参数。根据推论1可以获得各维修队列、采购队列的平均队长及方差等参数。

此外，备件从中心仓库向基地i运送的过程也可以看作是一个MAP/PH/1排队系统，这是因为备件进入运输渠道是一个MAP，而运输时间可以视为服务台服务时间，因此根据推论1容易确定运输中的备件个数分布。

4.3缺货量分布

记x0为中心仓库不可用备件数，则中心仓库缺货量的期望值可以表示为：

在到达过程为MAP的情况下，由MAP性质[15]可知：

令xi为基地i的不可用备件数，则基地i的期望缺货量则为：

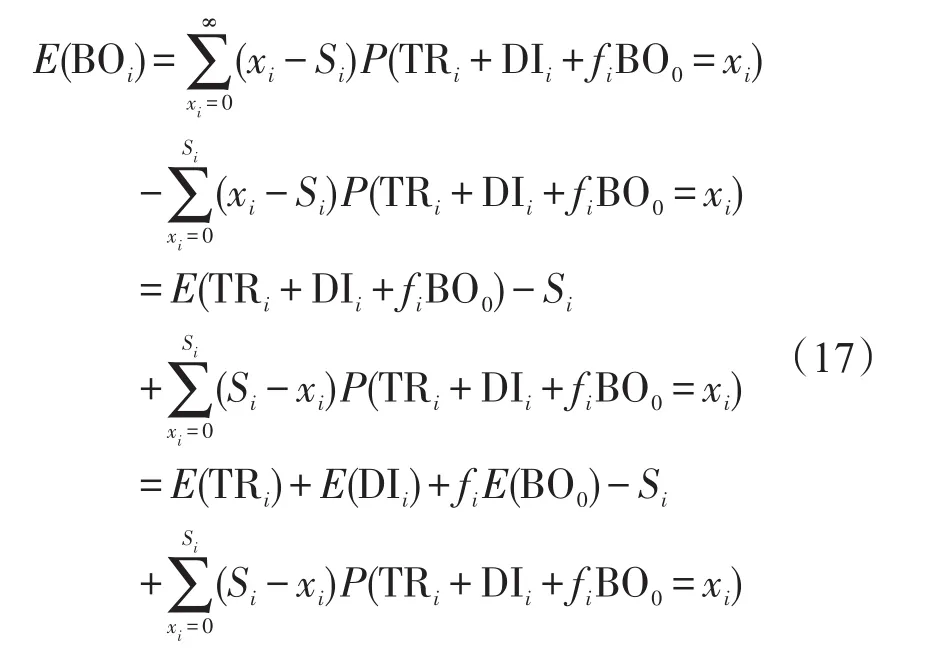
而BOi的两阶矩为：

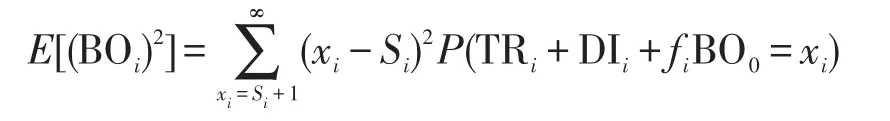
在获得各基地缺货量的期望和方差后，Grave[2]通过大量数据分析认为缺货量分布可以近似表示为参数a和b的负二项分布，因此本文亦直接采用该结论，由式（20）、式（21）可确定出a、b的值。

5　库存优化模型

定义PBO(S0，Si)为在给定S0和Si值后，基地i发生缺货的概率，由4.3节获得的缺货量分布容易得到：

因为各基地是一个并联系统，因此该多级库存系统的备件满足率可以表示为：

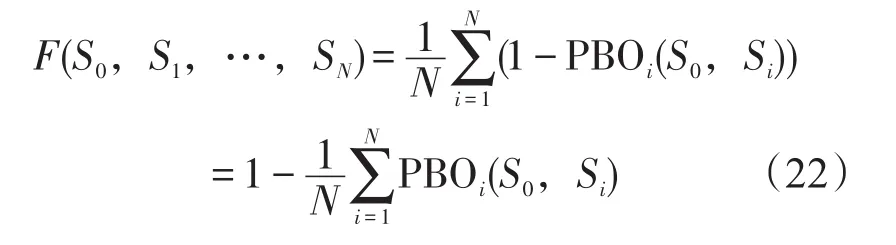
以总费用ctotal最小为目标函数，确定合适的S*=(S0，S1，...，SN)使得整个系统满足备件满足率约束。令c1、c2、c3、c4和c5分别为备件单价，单位备件库存费用，单位备件基地维修费用，单位备件中心仓库维修费用和单位缺货费用，因此该优化模型可以表示为如下形式：

式（23）中，Li和Wi分别表示各库存点库存量和维修队列长。

显然，备件满足率与单个库存点备件数之间存在单调递增关系；但A(S0，S1，...，SN)与{(S0，S1，...，SN)}的关系由于涉及多个相互独立的变量，就非常复杂了。对这类非线性整数规划模型而言，许多成熟的智能算法均能有效获得最优解。本文对智能算法不做深入研究，而直接采用遗传算法进行求解。

下面通过示例演示MAP和PH分布能够有效描述两级可修备件的（S-1，S）库存模型。

6　算例

某中心仓库负责4个基地的备件供应和维修保障任务。基地i的某型部件备件需求到达过程可以表示为MAP（D0(i)，D1(i)）；而各基地的维修时间分布、向中心仓库运输故障部件的时间分布可以分别表示为PH（αi，Ti）和PH（αiY，TiY），表1、表2是各基地的需求、维修及运输数据。

中心仓库的维修时间分布为PH(α0，T0)，采购备件的时间分布为PH(αC，TC)，其中：

而在中心仓库可修的概率则为p=0.79。c1、c2、c3、c4和c5分别为备件单价，单位备件年库存费用，单位备件基地维修费用，单位备件中心仓库维修费用和单位缺货费用，c1=26 800元，c2=90元，c3=440元，c4=1 900元，c5=7 000元。

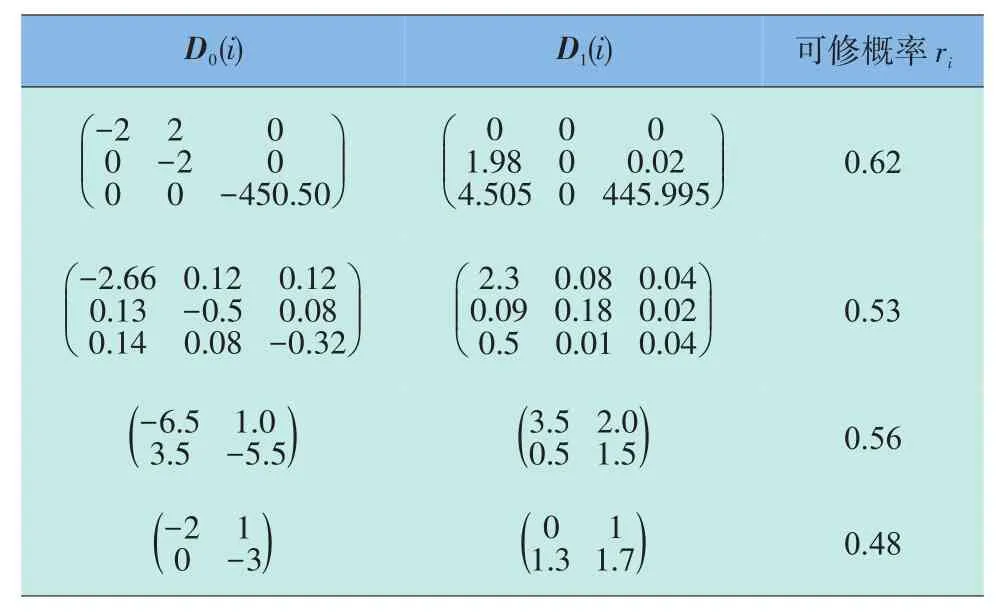
表1　各基地备件需求到达过程Table 1　The spare parts demand process of each base

表2　各基地备件维修时间分布及运输时间分布Table 2　The distributions of repair time and transit time for each base

下面利用4.3节获得的缺货量分布，研究中心仓库和各基地备件数对整个系统的备件满足率的影响。由于本优化模型包含5个自变量，因此为了便于更直观地了解备件数与备件满足率之间的关系，以中心仓库备件数S0、基地1备件数S1同时对系统备件满足率的影响为例进行说明。

如图3所示，令其他基地备件数均为0时，可以看到整个系统的备件满足率早期随着S0、S1增加而增加幅度较大；但当S0≥8并且S1≥2时，备件满足率就保持在0.711 2附近，说明要使满足率继续增加，必须调整其他基地的备件量。当其他基地的备件数均设为1时，系统备件满足率有大幅提升，迅速达到了0.937 4附近。而当其他基地的备件数均为5时，满足率上升则没有早期那么明显了，稳定在0.999 9附近。从图3可以看到，当给定其他基地的备件数时，S0、S1对满足率的影响十分相似。同时也表明无论中心仓库还是基地的备件数增加，均会使得备件满足率增加，只是增加的幅度与系统内其他仓库的备件数量密切相关；如果只增加S0,…,S4中任意一个，整个系统的备件满足率增长则十分有限。而当S0,...,S4均较大时，系统的备件满足率非常接近1，但此时仅购置费就会大幅上升。

图3　中心仓库和基地1备件数对备件满足率的影响Fig.3　The influence of the spare amount of central depot and base 1 on the system spare fill rate

在对备件满足率的分析过程中，人工对各库存点的库存量进行调整，发现当(S0，...，S4)=(6，0，2，2，1)时，满足率为0.9092；而(S0，...，S4)=(5，1，1，1，1)时，满足率达到了0.921 5。这说明为了提高系统的备件满足率，除了增加总的备件量外，还必须合理分配各单位的备件数。

7　结语

本文分析了以往多级可修备件库存模型中存在的问题，用MAP描述各基地的故障到达流，将维修与采购时间、运输时间均假设服从一般分布，建立了一个适应性更好的多级可修备件（S-1，S）模型，并给出了该系统缺货量分布。该类模型涉及到的库存优化算法是库存模型研究的一个重要方向，结合该类库存问题的实际背景和特点，开发更合理高效的启发式算法对本文模型在实际工作中获得有效应用有着重要的意义。本文建立的模型在计算时涉及到矩阵的运算，而目前高性能计算机和矩阵解析方法的应用能对大型矩阵的运算提供良好的支持，所以本文建立的模型具有很好的实用价值。

[1]Sherbrooke C C.METRIC：a multi-echelon technique for recoverable item control[J].Operations Research，1968，16（1）：122-141.

[2]Graves S C.A multi-echelon inventory model for a repairable item with one-for-one replenishment[J].Management Science，1985，31：1247-1256.

[3]Díaz A，Fu M C.Models for multi-echelon repairable item inventory systems with limited repair capacity[J].European Journal of Operational Research，1997，97：480-492.

[4]Sleptchenko A，Heijden M C，Harten A.Effects of finite repair capacity in multi-echelon，multi-indenture service part supply systems[J].International Journal of Production Economics，2002，79（3）：209-230.

[5]付兴方，李继军，李宗植.基于两级供应关系的可修复航材存储策略模型研究[J].系统工程理论与实践，2004，24（1）：111-115.

[6]Lau H C，Song H.Multi-echelon repairable item inventory system with limited repair capacity under nonstationary demands[J]. International Journal of Inventory Research，2008，1（1）：67-92.

[7]田乃硕，岳德权.拟生灭过程与矩阵几何解[M].北京：科学出版社，2002.

[8]Kim J S，Hur S，Kim T Y.A multiechelon repairable item inventory system with lateral transshipment and a general repair time distribution[J].Informatica，2006，17（3）：381-392.

[9]Asmussen S，Koole G.Marked point processes as limits of Markovian arrival streams[J].Journal Application of Probability，1993，30（2）：365-372.

[10]Asmussen S，Bladt M.Point processes with finite-dimensional conditional probabilities[J].Stochastic Processes and Their Applications，1999，82（1）：127-142.

[11]Chakravarthy S R.The batch Markovian arrival process：A review and future work，in advances in probability theory and stochastic processes[Z].A.Krishnamoorthy.New Jersey，2001，21-49.

[12]Huang Z，Liang L，Guo B.A general repairable spare part demand model based on quasi birth and death process[J].Acta Automacita Sinica，2006，32（2）：200-206.

[13]田乃硕.休假随机服务系统[M].北京：北京大学出版社，2001.

[14]Neuts M F.Matrix-Geometric Solutions in Stochastic Models-An Algorithmic Approach[M].Baltimore：Johns Hopkins University Press，1981.

[15]Breuer L，Baum D.An Introduction to Queueing Theory and Matrix-Analytic Methods[M].Dordrecht：Springer，2005.

A two-echelon（S-1，S）inventory model for repairable items based on markovian arrival process

Chen Tong，Li Fang，Di Peng
（Department of Management Engineering，Naval University of Engineering，Wuhan 430033，China）

This paper investigates a two-echolon inventory system with（S-1，S）policy that consists of several same repairable items and single repair facility，and assumes that the item demand occur according to a markovian arrival process（MAP），the repair time，ship time and procurement time follow the general distribution which is represented by phase-type（PH）distribution.Then a inventory optimization model with better description ability and analytical performance is given，and the probability distribution of backorder is obtained.Finally，a numerical example was given to illustrate the effectiveness of the model.

（S-1，S）policy；two-echelon inventory；repairable item；markovian arrival process

F253.4

A

1009-1742（2015）05-0113-07

2015-03-15

陈童，1980年出生，男，河南驻马店市人，博士，研究方向为装备综合保障，系统可靠性；E-mail：chentong@nudt.edu.cn