基于横向转运策略的多级库存配置建模与优化

阮旻智，刘任洋

（1.海军工程大学科研部，武汉430033；2.海军工程大学兵器工程系，武汉430033）

基于横向转运策略的多级库存配置建模与优化

阮旻智1，刘任洋2

（1.海军工程大学科研部，武汉430033；2.海军工程大学兵器工程系，武汉430033）

在多级维修供应体系下，采用备件横向转运补给策略能有效提高装备保障效率，针对该问题，依据生灭过程和METRIC理论，建立了多等级多层级装备备件的库存协调转运模型，并采用一种启发式算法对模型进行求解。在此基础上以装备可用度为约束，备件购置费用最低为目标，利用边际算法对库存方案进行优化。通过实例，模型的正确性通过仿真方法得到了验证，并与非转运条件下的优化方案比较，结果表明，本文构建的转运模型在提高装备保障效能方面明显优于非转运模型。

横向转运；多级维修供应；备件；边际优化；保障效能

1　前言

备品备件是装备正常维护检修的保障性物资，是实施装备维修的物质基础和重要保证，不仅影响着装备寿命周期费用，还直接影响装备的战备完好性及其作战效能。因此，如何在各级保障站点对备件进行合理的规划与分配是装备综合保障领域的热点问题。在部队传统的保障模式下，严格按照逐级的方式进行备件申请和补给，同级站点之间不考虑横向供应。然而在特殊的环境下，如对于长期在远海执行任务的舰船编队而言，在编队内部采用横向供应补给的模式，当装备故障而发生备件短缺时，相邻舰船对其进行横向补给要比从岸基仓库进行补给节省大量时间和空间，能够进一步提高装备保障效率。

对于该类问题，国内外已开展相关理论研究，Lee[1]在假设发生转运的站点完全相同的前提下研究了单个备件的两级库存转运系统，提出了转运模型的三个经典参数；Axsater[2]对备件转运模型进行扩展，考虑了转运站点不相同的情况，并对各站点稳态库存水平进行建模和求解。Kukreja[3]虽考虑的是一个单级系统，但其取消了Axsater模型中备件订购提前期服从指数分布的假设，拓展了模型的适用范围；Wong[4～6]围绕航空备件联合库存问题展开研究，采用横向转运和紧急调度相互结合的策略以减少总成本；然而，传统的转运模型假设转运能发生在各站点之间，这在某些实际场合不适用，针对该问题，Axsater[7]、Olsson[8]先后对基于单向转运策略的库存系统进行了研究，建立了具有不同优先级的站点转运模型。国内对该问题的研究相对滞后，大多都是对已有模型的扩展，霍佳震[9]对零备件库存多点转运的批量订购模型进行了研究，在已知订货量的前提下求得最佳订购点；张光宇[10]分别考虑了（S-1，S）和（R，Q）两种库存策略，提出了具有不同缺货费用的单向转运模型。在系统的开发与应用方面，欧美等国家和地区相继开发了VMETRIC、OPUS10、SIMLOX等一系列备件优化决策与方案评估工具，但对转运模块功能的设计还不够全面，只能适用于某些特定场合。国内到目前为止还未开发出具有通用、开放的备件规划决策工具。

尽管目前对于横向转运的理论研究不断趋于丰富与成熟，但将其运用于部队装备体系还存在不足[11]，主要表现为：首先是保障模式上的差异，大部分转运文献其研究对象针对商业供应链系统，供应模式一般为单级，最多两级，而部队现有保障模式根据其各军兵种编制体制的不同而呈现多样化的特点；其次是保障对象上的差异，现有研究仅限于考虑单个或多类无层次关系的备件，而军事装备具有复杂的系统层次结构，构建备件转运模型需要综合考虑系统结构。本文针对军事装备维修保障需求，研究装备备件协调转运与配置优化问题。

2　备件横向转运系统描述

考虑由基地级、中继级和使用现场级构成的三级库存转运系统，如图1所示。装备均部署在使用站点，装备中具有多个不同层次结构的可修复单元，包括：现场可更换单元（LRU）和车间更换单元（SRU）等。考虑备件的通用性和转运的便利性，只允许备件在由同一中继站点保障下的使用站点之间进行横向转运，而中继站点之间不发生转运。

图1　三级库存转运系统Fig.1　Three-echelon transshipment system

当装备发生故障，可通过备件更换的方式完成装备故障修复；故障单元LRU送往中继级进行维修，若其他同级站点有该LRU库存，则对故障现场进行转运补给，同时提供转运的站点向所属中继站点申领一项该备件，若其他同级站点均无该LRU备件，则故障现场发生一次备件短缺，并向中继站点申请常规补给；如果现场具备修复该LRU的能力，则不进行转运。由装备的层次结构可知，对故障单元LRU是其所属的SRU故障所致，SRU的送修、常规补给以及转运补给过程和LRU类似。

建模过程中除满足经典METRIC理论中的假设条件外，还必须做出如下几点补充说明。

1）使用站点维修时间较短，当现场无备件但能对故障件进行维修时，同级的其他站点不对其进行横向转运。

2）同级使用站点之间的距离远大于其所属中继站点的距离，因此横向转运时间可以忽略不计。

3　备件多级库存转运模型

3.1各站点备件需求率预测

当不考虑装备维修性、测试性等保障参数的影响时，根据装备工作强度、部署数量、装备组成结构及部件可靠性等参数可以计算得到第一层部件LRUi在使用站点 j的常规需求率为：

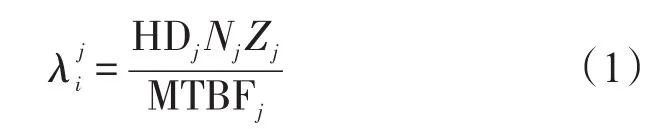
式（1）中，i为备件项目编号，j为保障站点编号；λ为备件平均需求率；HDj为装备在使用站点 j的工作强度（h/d）；Nj为装备部署数量；Zj为第j项部件在其母体中的单机安装数；MTBFj为第i项部件的平均故障间隔时间。

对于使用站点其他层级的部件i，其需求是由于维修i的母体组件l产生，则部件i在使用站点的常规需求率为：

对于非使用站点（中继站点和基地站点）j，第一层部件LRUi的需求为 j所属的下一级别站点m所有送修的LRUi之和，即有：

式（4）中，Unit(j)为由站点 j所属的下一级别站点的集合。

对于非底层站点 j的其他层级部件i，其需求除了考虑下一级别送修的故障件i外，还应考虑维修其母体组件l产生的对i的需求，则有：

式（6）中，下标i为备件编号，上标j为站点编号。h为使用站点无备件库存时的需求率；θ为备件缺货率；α为备件的直接满足率（无需通过转运满足）。

当使用站点有备件库存时，其需求等于不考虑转运时的常规需求加上转运至其他使用站点的额外需求。以下分别构建同一中继站点下存在两个和三个不同使用站点的需求率模型，三个以上的情况可按此法类推。

1）两个不同的使用站点。由于只有两个使用站点，无需考虑转运源问题，易得出使用站点1、2关于备件i有库存的需求率分别为：

2）三个不同的使用站点。假设当某一使用站点提出转运请求且其余两个均有库存时，选择这两个使用站点作为转运源的概率相同。易得出三个使用站点关于备件i有库存的需求率分别为[12]：

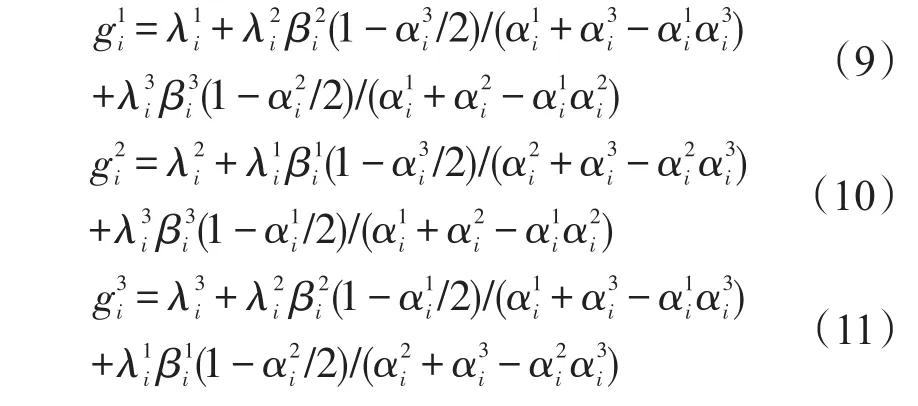
3.2备件周转量均值与方差

对于基地站点 j的底层部件i，其供应渠道数量即为故障件的在修数量：

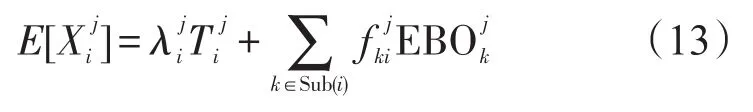
式（13）中，Sub(i)为部件i所属的所有分组件的集合。为站点 j因修理故障件i而产生的对其分组件k需求的比例，即：

对于中继站点 j的底层部件i，周转量包括在修数量以及上级站点的补给数量：

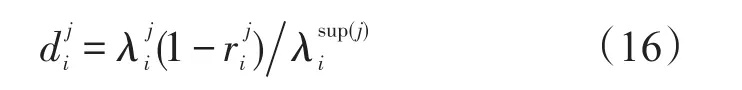
对于中继站点 j的其他层级部件i，备件周转量包括在修数量、上级补给的数量以及等待分组件k造成的修理延误数量：

由以上分析可知，一次具体的分组件k短缺正在延误该故障件i维修的概率为正在延误对下级站点补给的概率为故对于站点 j，延误故障件i维修的分组件k短缺数概率服从二项分布。同理，上级站点由于备件短缺造成对站点 j补给延误的概率也服从二项分布。则站点 j第i项备件的周转量方差为[13]：

根据式（12）～（18）即可算出基地站点和中继站点所有层级备件周转量的均值与方差，令为站点 j第i项备件的短缺数，其数学期望为方差为其中计算方法如下：

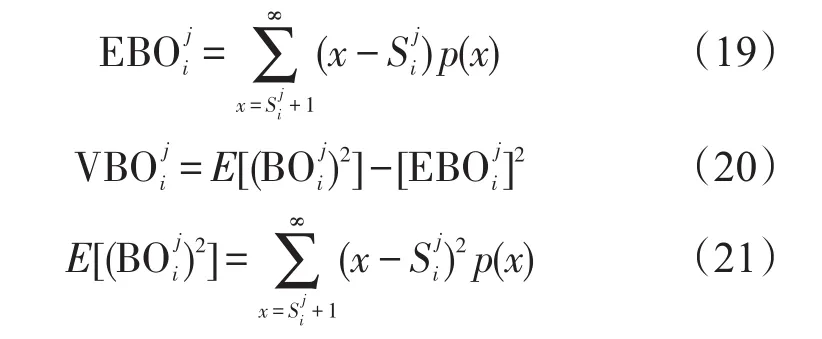
式（19）中，p（x）为备件周转量的稳态概率分布。根据文献[14]，当则p（x）服从泊松分布；当服从负二项分布；当时，p（x）服从二项分布。

3.3使用站点横向转运模型

根据Little方程，使用站点 j第i项备件的平均订购延误时间为：

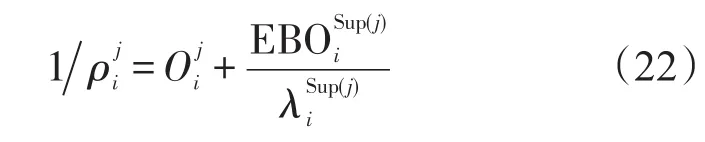
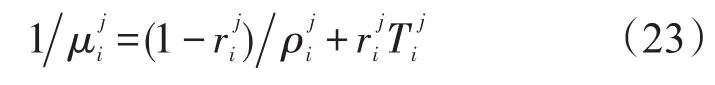
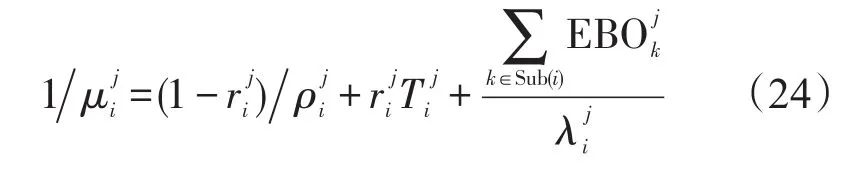
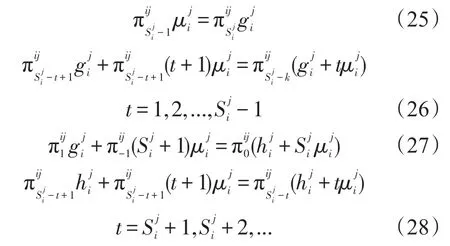
求解上述方程，得到使用站点 j关于备件i的稳态概率为：

其中，

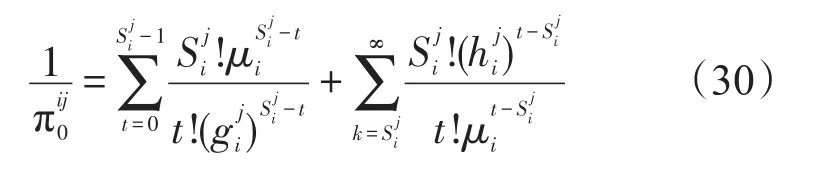
则使用站点j第i项备件的期望短缺数为：

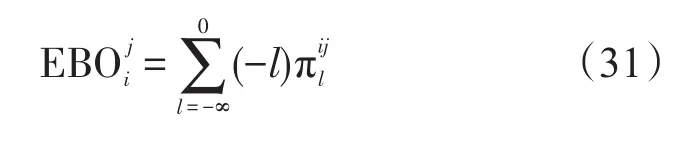
Step 2：根据式（22）～（31）计算使用站点库存稳态概率

4　备件配置优化模型

4.1保障效能指标的确定

备件保障效能指标是评价备件配置方案好坏的标准。常用的保障效能指标有装备可用度、备件满足率和保障延误时间等。

对于单个使用站点而言，装备可用度与装备第一层级现场可更换单元LRUi的短缺数存在如下关系[15]：

式（35）中，Inden（1）为装备所有LRU的集合。则对整个保障系统而言，平均可用度为：

式（36）中，Echelon（3）为保障组织结构中所有第三级别保障站点（使用站点）的集合。

备件满足率是指在规定的时间内，需要备件时不会出现备件短缺的概率。同样，装备系统级的备件满足率取决于其第一层级部件LRUi的满足率，即使用站点j的装备系统级备件期望满足率为：

因此整个保障系统的平均备件满足率为：

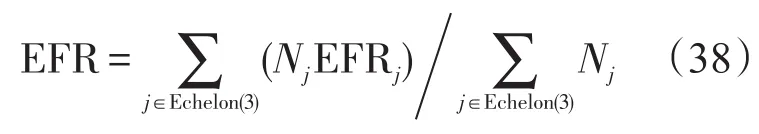
保障延误时间是指平均等待备件的时间。对于单项备件，其值可以根据备件短缺数除以备件需求率得到；对于装备系统级的保障延误时间可由各LRUi的保障延误时间加权得出。则使用站点 j装备系统级的平均保障延误时间为：

由此整个保障系统的平均备件满足率为：

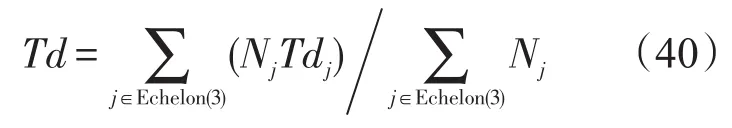
4.2库存优化模型及求解

备件的库存优化问题可描述为以规定的装备可用度、备件满足率或保障延误时间等保障效能为约束指标，寻求整个保障体系内费用的最低化，即：

本文以可用度A作为约束指标，运用边际分析法求解上述模型，具体步骤如下。

Step 1：初始化所有站点的备件配置数量，令备件库存量矩阵s=0。

Step 2：计算站点 j第i项备件的边际效应值：

这里，ones(j,i)表示站点 j第i项备件库存量为1，其余全为0的矩阵。

Step 3：将δ(j,i)值最大者所对应的站点 j上备件i库存量加1，由此得到新的库存量矩阵s。

Step 4：计算在新库存方案s下整个保障系统的可用度A，并与规定的可用度指标A0比较，如果A≥A0，算法结束，此时的s即为最优库存配置结果；反之则转入Step 2进行迭代。

5　算例分析

假设一个三级保障系统，包含一个基地站点（D0）、两个中继站点（I1、I2）和五个使用站点（B1～B5），站点之间隶属关系如图1所示。现对配置在使用站点的某型装备备件库存量进行优化。其中，由中继站点I1保障下的使用站点B1～B3，以及由中继站点I2保障下的使用站点B4、B5可以通过转运满足保障要求。装备组成结构如图2所示，装备在五个使用站点的配置数量分别为[8，6，6，10，5]，平均每天工作时间为8 h。备件的相关参数如表1所示。

表1　备件参数Table 1　Spare parts parameters

保障系统中基地站点对两个中继站点的常规补给时间分别为[8，6]天，中继站点对五个使用站点的常规补给时间分别为[3，3，3，4，4]天。

设规定的可用度指标A0为0.95，边际算法迭代77轮后得到备件在各个保障站点的最优配置方案，如表2所示。迭代的费效曲线如图2所示（为了统一量纲，将保障延误时间进行[0，1]区间的归一化处理）。

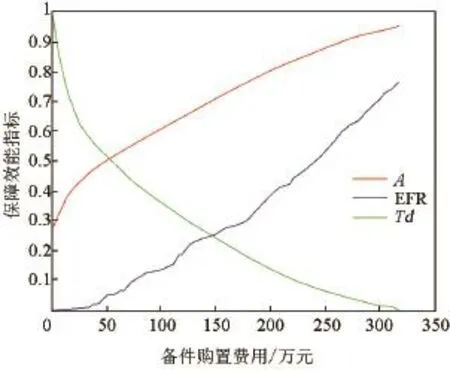
图2　转运模型费效曲线Fig.2　The optimal curves of effectiveness vs cost

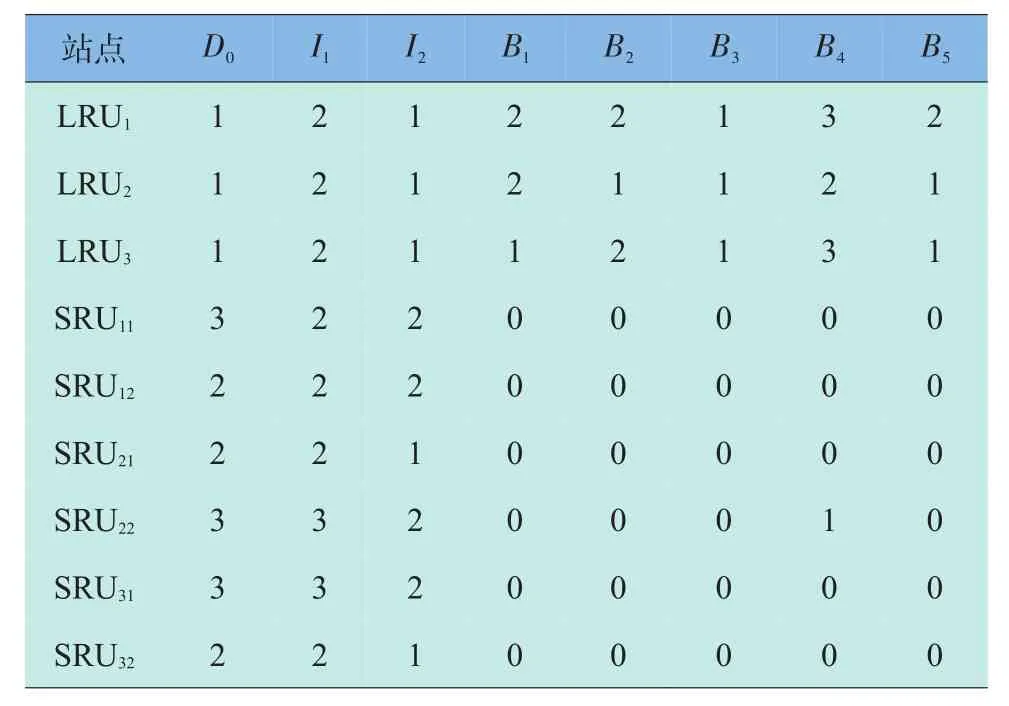
表2　转运条件下备件最优配置方案Table 2　Spare parts optimization project with lateral transshipment

采用仿真方法对模型转运参数进行验证。整个保障系统为一个典型的离散事件系统，仿真程序中包含备件需求发生模块、正常补货模块、横向转运模块以及故障件维修模块。为了使系统趋于稳态，将备件需求发生的总次数设为2 000，仿真时钟按事件发生的逻辑顺序转入相应模块。这里，的仿真估计值由统计得到的备件需求被自身库存满足的次数除以备件需求发生的总次数得到；的仿真估计值则为备件需求被其他使用站点满足的次数除以备件需求发生的总次数。

表3为分别采用本文算法和仿真方法得到的参数值（受篇幅限制，只选取了一部分），每种方法下对应的三列数值分别为使用站点B1、B4和B5相应备件的参数结果。通过对比可以看出本文结果与仿真结果基本相符，且算法迭代均在5次以内收敛，说明了本文构造的模型正确，算法效率高。

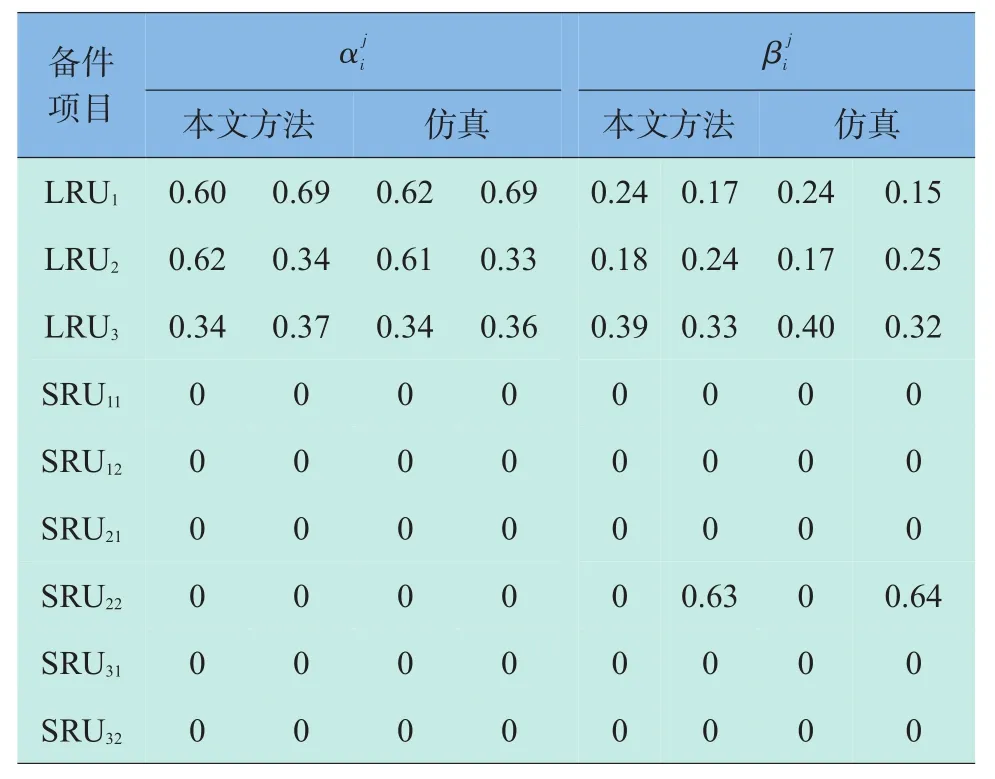
表3　本文方法与仿真方法转运参数结果对比Table 3　Comparisons of transshipment parameters with simulation

为了进一步体现转运模型的保障效果，将其与非转运模型进行对比，由于两种模型设定了同样的可用度约束指标，因此分别以期望满足率EFR、保障延误时间Td以及备件购置费用C进行分析对比，以表示保障效能提高比例。从表4可以看出，在满足相同可用度指标的前提下，转运模型的期望满足率提高了13.02%，保障延误时间降低了5.35%，同时备件购置费用减少了11.10%，其保障效能要明显优于非转运模型。

表4　转运与非转运保障效能对比Table 4　Comparisons of support effectiveness with non-lateral transshipment

6　结语

本文针对多级维修供应的保障模式，从提高装备保障效能入手，建立了包含多个层次结构的装备备件多级库存转运模型，得到了最优库存分配方案。通过与传统非转运模型的对比说明了本文所构转运模型在提高装备保障效能方面的优越性，为装备保障人员在不同的任务背景下制定合理的备件方案提供一定的决策依据。

值得注意的是，本文模型只考虑了使用站点之间距离很近的情况（从而忽略转运时间），因为在部队现有上下级保障体制中，如果同级之间距离与上级站点相当或是相差不多时无需采用横向供应策略。

[1]Lee H L.A multi-echelon inventory model for repairable items with emergency lateral transshipments[J].Management Science，1987，33（10）：1302-1316.

[2]Axsater S.Modeling emergency lateral transshipments in inventory systems[J].Management Science，1990，36（11）：29-40.

[3]Kukreja A，Schmidt C P，Miller D M.Stocking decisions for low-usage items in a multilocation inventory system[J].Management Science，2001，47（10）：1371-1383.

[4]Wong H，Houtum V G-J，Cattrysse D，et al.Simple efficient heuristics for multi-item multi-location spare parts systems with lateral transshipments and waiting time constraints[J].Journal of Operational Research Society，2005，56：1419-1430．

[5]Wong H，Cattrysse D，Oudheusden D V.Inventory pooling of repairable spare parts with non-zeros lateral transshipment time and delayed lateral transshipments[J].European Journal of Operational Research，2005，165：207-218.

[6]Wong H，Houtum V G-J，Cattrysse D，et al.Multi-item spare parts systems with lateral transshipments and waiting time constraints[J].European Journal of Operational Research，2006，171：1071-1093.

[7]Axsater S.Evaluation of unidirectional lateral transshipments and substitutions in inventory systems[J].European Journal of Operational Research，2003，149：438-447.

[8]Olsson F.An inventory model with unidirectional lateral transshipments[J].European Journal of Operational Research，2010，200：725-732.

[9]霍佳震，李虎.零备件库存多点转运的批量订货模型与算法[J].系统工程理论与实践，2007（12）：62-67.

[10]张光宇，李庆民，李华.零备件的多点库存单向转运模型与算法[J].航空学报，2013，34（5）：1092-1100.

[11]阮旻智，李庆民.（R，Q）库存策略下消耗件的协同订购方案优化[J].北京理工大学学报（自然科学版），2013，33（7）：680-684.

[12]李虎.零备件库存管理优化研究[D].上海：同济大学，2007.

[13]阮旻智，李庆民，黄傲林，等.有限维修渠道约束下多级维修供应系统库存控制[J].航空学报，2012，33（11）：2018-2027.

[14]贺步杰.装备备件最优库存建模——多级技术[M].北京：电子工业出版社，2008.

[15]阮旻智，李庆民，张光宇，等.多约束下舰船装备携行备件保障方案的确定方法[J].兵工学报，2013，34（9）：1144-1149.

[16]张光宇，李庆民，郭璇.基于横向转运策略的可修备件多点库存建模方法[J].系统工程与电子技术，2012，34（7）：1424-1429.

Modeling and optimization for multiechelon spares inventory configuration with lateral transshipments

Ruan Minzhi1，Liu Renyang2
（1.Department of Researchirg，Naval University of Engineering，Wuhan 430033，China；2.Department of Weaponry Engineering，Naval University of Engineering，Wuhan 430033，China）

Under the multi-echelon repair and supply system，spares supply with lateral transshipments is an effective approach to improve support effectiveness.Focus on this issue，according to theories of life-death process and mutil-ehcelon technique for recoverable item control（METRIC），spares lateral transshipments model under multi-echelon multi-indenture system is built，and heuristic algorithm is introduced to get the model result.Take the equipment availability as constraint and spares cost as objective，the spares inventory is optimized by marginal algorithm.Through the given case，the model correctness is verified by simulation，compared with the result without transshipments，numerical studies show that our model is superior in improving the support effectiveness of equipment.

lateral transshipments；multi-echelon maintenance supply；spare parts；marginal optimization；support effectiveness

E911；TJ761.1

A

1009-1742（2015）05-0106-07

2015-03-06

国家部委级十二五预研项目（51304302，51304303）

阮旻智，1983年出生，男，湖北武汉市人，博士，主要研究方向为装备保障资源优化与仿真；E-mail：ruanminzhi830917@sina.com