瓷砖抛光过程建模与仿真*
2015-11-30朱成就
朱成就
(广东工业大学机电工程学院,广东广州 510006)
瓷砖抛光过程建模与仿真*
朱成就
(广东工业大学机电工程学院,广东广州 510006)
瓷砖的抛磨影响因素众多,实际磨削加工时容易出现漏抛、返抛现象。对陶瓷抛光机磨头进行运动学分析,并基于不同粒度号的磨粒在一定压力下的加工深度模型,探讨抛光机磨头转速、横梁摆动频率、传送速度对瓷砖抛光加工表面均匀性的影响,然后结合磨削机理使用MATLAB软件对陶瓷抛光过程进行仿真。最后使用多组不同的运动参数进行模拟试验,分析不同条件下抛光的均匀性影响。
陶瓷抛光机;均匀性;运动参数;仿真
0 引言
为达到表面平整、光亮、色泽鲜明等生产要求,瓷砖刮平工序后需要进入抛光机抛磨。在实际生产中,抛光工艺复杂,影响抛光质量的因素众多,其中抛光机的运动参数对抛光制品表面的均匀性影响规律是国内外研究的热点问题。Sousa等[1]建立了磨粒在抛磨过程的运动学方程,分析运动参数对加工过程的影响。Sousa和Aurich[2]通过建立瓷砖表面抛磨的时间模型,分析瓷砖横向与机器摆动的联合运动对加工表面的影响并作优化分析。国内,许雄超、王世旺[3]建立了瓷砖抛光均匀性的计算机仿真模型,探讨了抛磨机各运动参数和几何参数对抛光砖磨削均匀性的影响。陈彩如[4]等结合Preston方程,综合考虑磨削速度、磨削时间与磨削量的影响建立分析模型,得出当量磨削量的分布规律。
但是这些模型都是以抛光机平面运动轨迹为研究,忽略磨粒垂直方向的磨削状况,并没有反映出真实的磨削情况,而且大多数都是针对同一规格参数的磨粒进行研究,没有结合抛光机上所有磨粒粒度号对瓷砖加工的相互作用。针对这些问题,本文在考虑不同粒度号磨粒的垂直磨削量对抛光均匀性影响的基础上,对抛光运动进行仿真与试验研究。
1 抛光机工作原理
本文以一种新型的摆动式抛光机为原型,陶瓷抛光机的加工原理如图1所示。抛光机整体是横梁带动所有磨头做前后摆动,而每个磨头有6个磨块。抛光机每个磨头工作原理如图1(a)所示。图1(b)为磨块座展开的示意图。其工作原理为电动机通过小带轮、大带轮带动主轴旋转,然后通过刚性连接带动主动齿轮,继而带动从动齿轮和凸轮旋转。磨盘在公转的同时,通过差动轮系,使凸轮相对磨盘产生一个相对运动,凸轮驱动主动摆杆,主动摆杆又驱动从动摆杆。使连接在摆杆上的磨块做往复的摆动。为了保持磨粒均匀的消耗,每个磨块座都会绕其自身的中心轴线摆动,尽管这种方式有助于所有磨粒与砖面的接触,但是接触的有效面积是不变的,因此为简化磨削运动模型,本文根据实际测量定义两者接触面积大小,并假设磨块保持恒定位置磨削,并不摆动。

图1 陶瓷抛光机原理图
2 抛光过程运动模型
2.1 磨粒轨迹分析
为方便分析,假设瓷砖静止不动,磨头做相对运动进行磨削加工,磨头上磨粒的平面运动轨迹[1]如图2所示。首先建立直角坐标系,轴与抛光砖移动的方向平行;轴代表磨头横向摆动的方向并与轴垂直,那么磨块任意一点P的运动轨迹可由向量表示。向量在t0时刻的位置由如下组成:瓷砖移动的方向E,磨粒随磨头自转运动R和横梁横向移动OL。
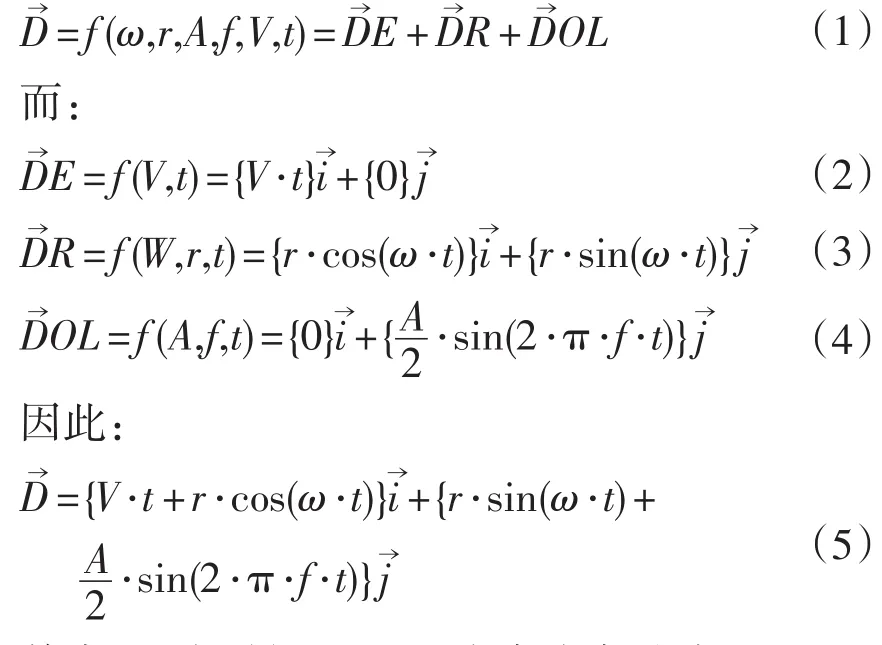
其中:t为时间,s;w为磨头角速度,rad/s;V为传送带的速度,mm/s;f为横向摆动的频率,s-1;A为摆动的幅度,mm;r为磨粒到磨头的中心的距离,mm。
2.2 磨粒切削深度分析
抛光过程中,磨块上的磨粒与瓷砖直接接触进行抛磨,因此磨粒的形态大小直接影响到抛磨质量[5]。陶瓷抛光机上一般有14~20个磨头,而瓷砖的抛磨过程分为粗加工和精加工,在不同的磨削阶段,磨块的粒度号是不同的。可见,对磨粒建立准确的数学模型能够更好地反映出抛光过程。
2.2.1 有效磨粒数分析
磨粒的直径根据粒度号(例如,80#)的大小服从正态分布[6]。粒度的最大直径为dmax,最小直径为dmin,而平均直径为dmean:

图2 磨粒运动轨迹分析图

dmax与dmin的值由粒度号决定(可参考文献[5]的测量值)。
使用dgx表示磨粒的直径,并定义变量x:
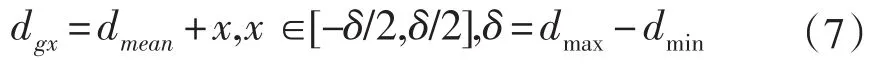
如图3所示,对于x的相邻区间,磨粒直径的概率表示为服从标准差的正态分布:
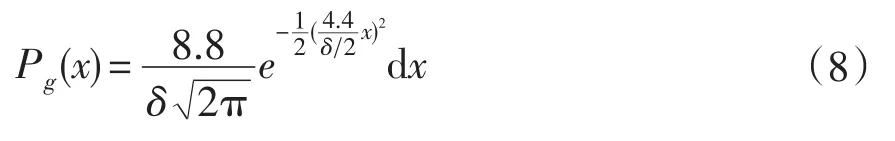
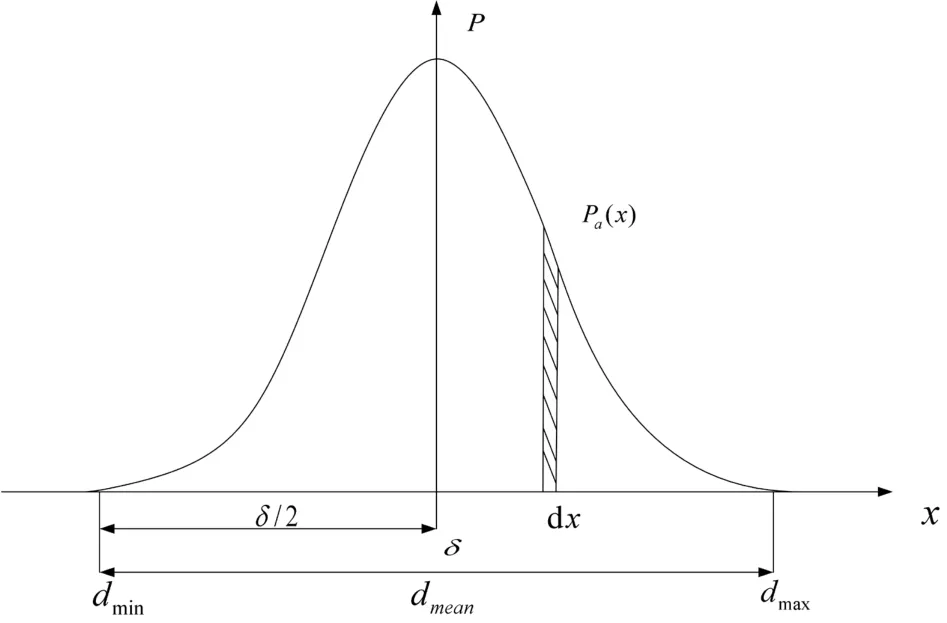
图3 磨粒直径服从σ=(δ/2)/4.4正态分布图
设单位体积的磨粒数为Nv,因此,磨块的单位体积中,直径为dgx的磨粒数为:
透光良好的越冬水体、水中无大量浮游动物、水色又较深(透明度低于50cm)而溶氧仍大幅度下降时,就应当施肥。对一些长时间不能补充水或补水而水源营养盐含量极少的水体,在封冰后不久就应着手施肥。生物增氧施用化肥时,最好使用磷肥,少用或不用氮肥,避免氨氮升高,致鱼中毒。

这里假设磨粒的形状为夹角为136°的正四棱锥,所以在每单位体积当中,直径为dgx的总体积为:其中,θ为四棱锥夹角。
因此单位体积中所有磨粒的总体积ϕ为:而ϕ可以由磨块的组织号N得出:

结合上面式(9)和式(10),单位体积上的磨粒数Nv为:
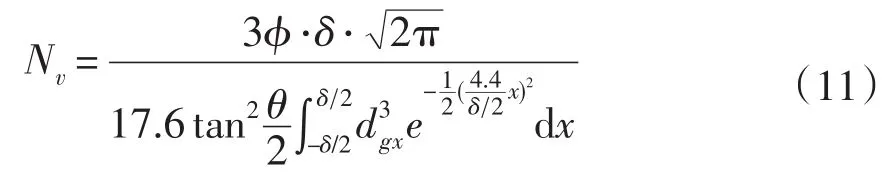
2.2.2 磨粒压痕深度分析
若把陶瓷砖磨削中的磨粒与工件的相互作用看做小规模的压痕现象,则磨粒对硬脆材料的作用如图4所示。
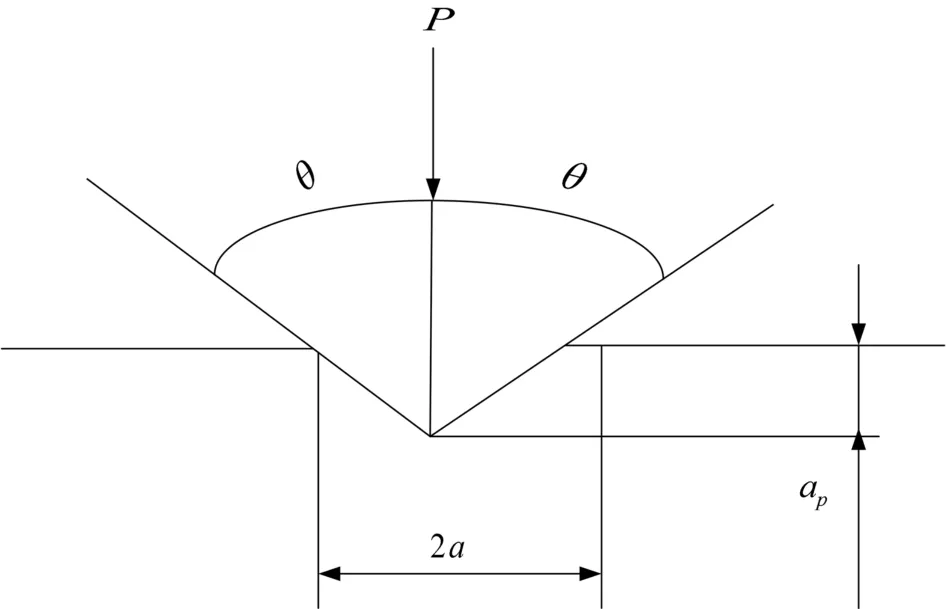
图4 磨粒的压痕模型
当压头(磨粒)在负载P作用下压入陶瓷表面时,压头下部的试件材料(瓷砖)发生非弹性流动[7]。若压痕是通过材料的显微塑性流动形成的,则作用于压头上的载荷P与压痕特征尺寸2a有如下关系:

由图4知,压痕特征尺寸2a=2ag·tanθ,θ为压头或磨粒锥顶半角。因此可得,磨粒切削厚度ag为:

其中ξ为压头几何因子,维氏压头ξ=2;H为陶瓷材料的硬度,这里取维氏硬度H=5.7± 0.1GPa。
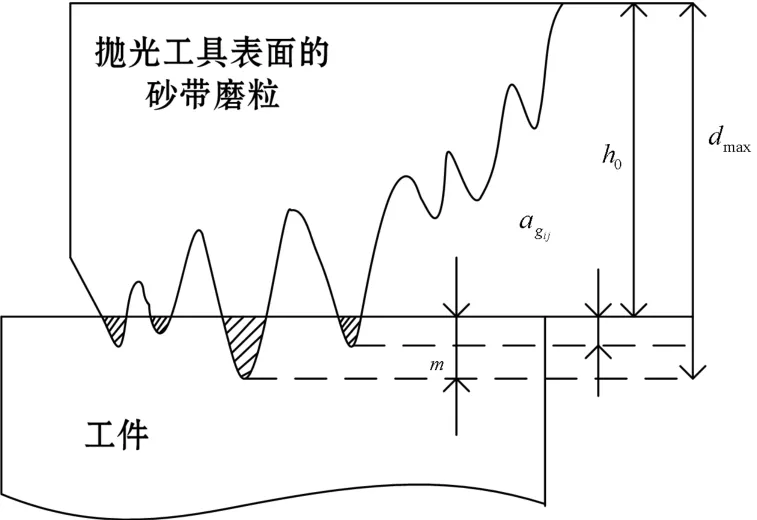
图5 磨粒压印深度图
磨块在一定的压力下并不是所有磨粒都压入相同的深度,而是由压力与最大磨粒的出刃高度决定的。图5为磨粒出刃高度的分布示意图。图中,dmax为磨粒最大的直径,h0为原点距工件表面的距离,利用式(13)求出的值作为最大磨粒的压痕深度m。于是h0=dmax-m,磨块中其他磨粒的压痕深度为:

3 仿真与试验研究
3.1 仿真实验流程
陶瓷制品的表面粗糙度和光泽度是衡量抛光质量的主要指标,可以使用抛磨后的瓷砖加工的表面方差S2表征抛光质量;方差是一种反映相对离散程度的数值,因而适合于不同性质数据的研究与比较。可以看出方差越小磨削就越均匀,即抛光质量越好。
由于磨粒的大小不一,离散程度难以确定,为保证仿真模型的正确性,这里以磨块离散后的区域单元运动轨迹作为磨粒的运动轨迹,并统计出区域单元的有效磨粒数,具体做法如下:将磨块均匀的离散为a×b个相等区域,计算每个单元区域的有效磨粒数Sn=M·Nv,M为区域的面积,利用概率密度函数Pg(x)(式(8))求出Sn个磨粒的直径,根据给定的压力使用式(14)计算出磨粒的压痕深度,最后求出其平均值为表示磨块某一区域单元的磨削深度。
将抛光砖表面均匀离散为n×n个相等的区域,使用矩阵R(i,j)记录瓷砖表面的加工深度,瓷砖左下角记为R(1,1)。抛磨过程中,使用式5确定每Δt时间磨块的各单元的位置,若在瓷砖范围内,则根据该区域的磨削深度计入矩阵R(i,j)中。最后通过抛光砖抛磨后的表面加工深度计算磨削的平均值和方差和作为抛光均匀性分析的指标。程序流程如图6所示。
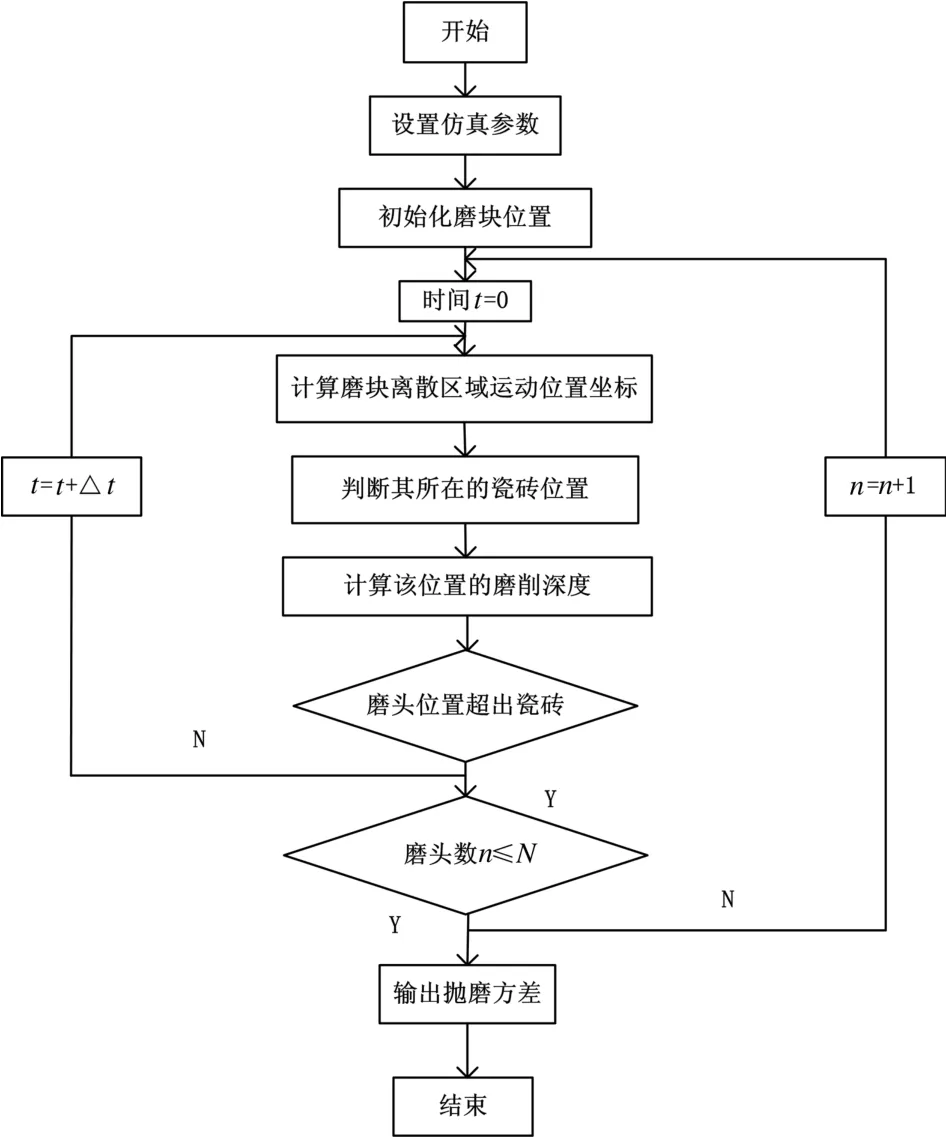
图6 程序流程图
3.2 实验结果分析
经过刮平定厚机对瓷砖表面进行铣刮加工之后,瓷砖才进入抛光机抛磨,瓷砖表面粗糙并带有刮痕。因此在仿真实验开始前,需要生成符合实际进入抛光生产前的瓷砖特性的虚拟瓷砖。这里假设瓷砖的原始高度为12 mm,在此基础上加上标准正态分布生成的随机数来初始化瓷砖。将瓷砖离散成160×160个单元,而磨块则离散成36 ×12个单元,分别采用多组不同的运动参数进行仿真对比试验,主要的实验参数如表1所示,磨头抛光的实验对比结果如图7所示。
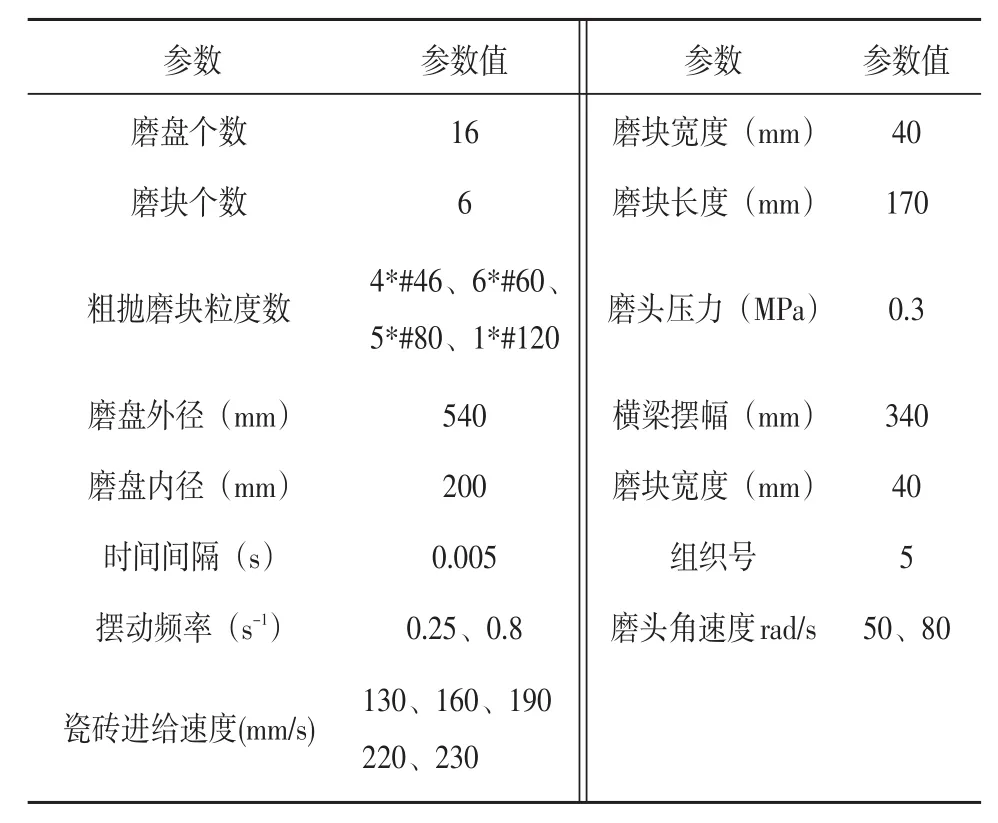
表1 仿真参数表
从图7可以看出,在其他加工参数相同的情况下,磨头角速度对方差影响较大,角速度w越大,方差S2越大,这是由于角速度的增大导致磨粒在瓷砖单位区域停留的次数增加,使得垂直方向的磨削量增加,而抛磨过程中横梁是以摆动的形式运动,瓷砖存在抛光不均的情况,最终造成砖面加工的方差增大;因此合理降低角速度有利于提高抛磨质量。另一方面在磨头角速度不变的情况下,不同的摆动频率f在一定的进给速度V范围内有起伏,这是因为磨盘中心点平面的运动轨迹主要受f与V影响,同时会影响到磨粒在砖面上的停留时间,两者的相互作用使方差增大或减小;选择适当的摆动频率和进给速度控制好砖面磨削的时间,可以防止出现漏抛、返抛现象。
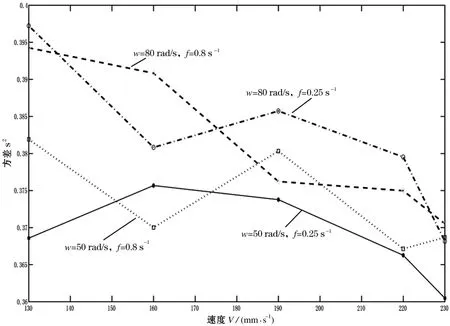
图7 实验对比结果图
4 结论
本文分析了陶瓷抛光机的运动规律,并根据磨块的磨粒号与组织号量化磨粒的大小及加工深度,最后结合陶瓷砖进给速度、磨盘角速度、横梁摆动频率三者对抛光机磨削运动的影响,建立瓷砖抛磨的均匀性模型,得出抛磨深度的分布规律,最后使用多组参数在计算机上用MATLAB软件进行仿真实验。仿真的对比实验反映出三种运动参数对抛光均匀性影响。这为进一步做参数优化,改善抛磨质量具有十分重要的意义。
[1]Sousa FJP,Aurich JC,Weingaertner WL,Alarcon OE. Kinematics of a single abra⁃sive particle during the in⁃dustrialpolishing process of porcelain stoneware tiles[J].JEurCeram Soc 2007, 27 (10) :3183-90.
[2] Fábio J.P.Sousa,Jan C. Aurich.Optimization of the Kinematics Available in the Polishing Process of Ceram⁃ic Tiles by Computational Simulations[J].Journal of the American Ceramic Society Volume 92,pages 41-48,2009.
[3]许雄超,王世旺.基于陶瓷抛光机抛磨运动建模及试验研究[J].机械设计与制造,2008(9):132-134.
[4]陈彩如,谭建平.大规格陶瓷砖抛光过程仿真与试验研究[J].中国陶瓷,2008,44(2):45-47.
[5]纪宏波,彭岩,周芬芬,等.氧化锆陶瓷平面零件超精密研磨实验的研究[J].机电工程,2013(09):1059-1062.
[6] Jiang J,Ge P,Hong J.Study on micro-interacting mechanism modeling in grinding process and ground sur⁃face roughness prediction[J].The International Journal of Advanced Manufacturing Technology, 2013, 67(5-8):1035-1052.
[7]任敬心,华定安.磨削原理[M].北京:电子工业出版社,2011.
The Modeling and Simulation Study upon Ceramic Tile Polishing Process
ZHU Cheng-jiu
(College of Mechanical and Electronic Engineering,Guangdong University of Technology,Guangzhou510006,China)
Many factors affect the polishing of ceramic tile.In the actual grinding process,it is easy to occur the phenomenon of without polishing in certain areas or polishing again.This paper mainly analyzes kinematics of polishing head in polisher and based on the model of grinding depth under certain pressure with different grain size,studies the influence of rotational speed of the abrasive disk,frequency of the lateral oscillation forward and speed of the polishing line on homogeneity of polishing surface,then combined with the grinding mechanism,using MATLAB software to simulate the polished ceramic process modeling.Finally,using multiple groups of different parameters to simulate,analyzed the effects of the uniformity in different conditions of polishing.
polisher;uniformity;movement parameter;simulation
TH16
A
1009-9492(2015)10-0061-05
10.3969/j.issn.1009-9492.2015.10.015
朱成就,男,1987年生,广东江门人,硕士研究生。研究领域:智能制造、低碳制造。
(编辑:向 飞)
*广东省自然科学基金(编号:501130093)
2015-04-07
