随机型混合U型装配线的平衡研究

郑晨鸣，段移庭

（广东工业大学机电工程学院，广东广州 510006）

随机型混合U型装配线的平衡研究

郑晨鸣，段移庭

（广东工业大学机电工程学院，广东广州 510006）

针对混合产品和作业元素时间随机的U型装配线平衡问题，建立了数学模型并提出一种改进的遗传算法求解。在给定的节拍和完工率下，以最小工作站数和各产品负荷均匀为目标，设计改进的遗传算法求解作业元素分配序列。最终结合实例验证方法是有效的。

混合产品；U型装配线；作业时间随机；遗传算法

U型装配线平衡问题是直线型装配线平衡问题在布局上的一个延伸。因此在考虑U型装配线平衡问题研究现状前有必要描述下直线型装配线平衡的思路发展。装配线平衡问题最早由Salveson的文献[1]中提出，定义为将一系列作业元素按照一定先后次序分配到装配线上的各个工作站内，满足各个工作站内的作业元素时间总和不超过一定节拍的同时，使得每个工作站的空闲时间最小，然后用动态规划和最短路径等方法求解装配线平衡问题。1966年Arcus A.L在文献[2]中提出一种COMSOAL(Computer Method of Sequenc⁃ing Operations for Assembly Line)的方法来解决装配线平衡问题，这种方法综合了计算机、随机抽样、蒙特卡洛等技术，是启发式算法外的另一种有效解决方法。

在装配线平衡问题发展了40多年后的1994年，Miltenberg J在文献[3]中首次提出JIT模式下的U型装配线平衡问题（U-Line Balancing Prob⁃lem，ULBP），即U型装配线在平衡分析时可以从前后双向搜索作业元素，在U型装配线上首尾两个作业元素是可以被分配到一个工作站的，这是U型装配线在作业分配时和直线型装配线的明显区别。1998年Miltenberg J的学生Sparling D在文献[4]中率先研究了混合U型装配线的平衡问题，文章提出将混合装配线平衡问题通过得出综合作业先后顺序图来等效为单一品种装配线平衡问题，提出装配线作业分配和投产排序都会影响到U型混流装配线的平衡，并在文献[5]中对U型装配线平衡理论和实际应用进行了总结。同年Ajen⁃blit D.A和Wainwright R.L在文献[6]中用遗传算法优化ULBP的两个目标：最小化工作站总的空闲时间和均衡工作站负荷，同时提出遗传算法是求解ULBP问题的优良选择。1999年Scholl A和Klein R在文献[7]中提出ULO(U-line optimizer)方法，ULO是一种在利用分支定界法设定的程序中高效寻找最优解的过程，最多可以求解297个作业元素的U型装配线平衡问题。2001年Erel E，Sabuncuoglu I和Aksu B.A在文献[8]中运用基于模拟退火算法求解ULBP。2005年Agpak K和Gok⁃cen H在文献[9]中用最短路径法求解ULBP，之后于2006年用目标规划方法求解了ULBP。

混流装配线是可以在同一装配线上混合的、连续的装配几种结构相近、工艺相似产品的装配线。首次解决混流装配线平衡问题的是Thomo⁃Poufos N.T，1967年他在文献[10]中运用联合先后顺序图的概念把混流装配线转化为单一品种装配线来处理，从而把单一品种装配线的平衡技术和方法运用到混流装配线后解决了混流装配线平衡问题。1970年Roberts S.D和Villa C.D在文献[11]建立了整数规划模型来求解混流装配线的平衡问题。2001年Korkirnazel T和Meral S在文献[12]提出了JIT的两个目标：(1)工作站间的负载均匀；(2)零部件消耗率均匀。重点讨论零部件消耗率为目标保证两个方面：(1)产品生产量与需求相当；(2)制造过程中零部件使用率始终保持稳定。2002年Joseph B等在文献[13]提出用新的启发式算法解决在面向订单情况下的混流装配线平衡问题。这是因为传统的装配线平衡问题只考虑最小化工位数，但是在实际生产中，生产效率才是企业最看重的因素。2005年Agpak K和Gokcen H在文献[14]提出用“0-1整数规划模型”来求解混流装配线问题。2004年Simaria A.S和Vilarinho P.M在文献[15]提出用迭代基因算法来求解混流装配线平衡问题，优化目标是给定操作工人数求得最大化生产率。2007年陆叶、苏平在文献[16]中通过改进的遗传算法和系统实现的方法分析了混合装配线的平衡问题。2008年于兆勤等在文献[17]中利用了遗传算法和仿真分析相结合的方法分析了混合装配线平衡问题，主要解决的是混合装配线中由于产品作业时间的差异带来的工作站间负荷不均匀的问题。

随机型装配线就是作业时间随机的装配线（Stochastic Assembly Line），对应的就是随机型装配线平衡问题（Stochastic Assembly Line Balancing Problems）。Moodie C.L和Young H.H于1965年在文献[18]最早研究不确定作业时间的装配线平衡问题，方法还是先假设作业时间是服从正态分布的随机变量来求解的。1995年Nkasu M.M和Leung K.H最早在文献[19]采用改进的COMSOAL方法分别假设模拟了作业时间服从正态分布、指数分布、伽马分布、均匀分布和韦布尔分布下的装配线平衡问题，同时对结果进行了详细的统计分析。1998年Urban T.L在文献[20]利用两阶段的线性整数规划方法建立了概率模型对不超过28个作业元素的装配线平衡问题求得了最优解。2010年黄卫平等在文献[21]中运用集束搜索算法对随机型混合模式装配线平衡问题进行了求解。2013年朱华炳等在文献[22]中研究了随机型混流装配线动态排序问题。2006年Chiang W.C等在文献[23]提出一种混合启发式算法来求解中等规模的SUAL⁃BP。2012年Seyed M.K等在文献[24]中提出了一种求解U型混流装配线第一类平衡问题的方法，即通过以最小化工作站数和最大化装配线完工率来求解。2013年Chun-Hung C等在文献[25]中提出了用遗传算法来搜索U型装配线平衡问题的最优解。

到目前为止，关于作业时间随机的装配线论文研究还是相对其他方面的研究较少的，本文在研究作业随机的同时，还需要考虑混合产品对混流装配线平衡结果的影响。而无论是作业时间随机、混合产品还是U型布置的装配线问题都是目前企业中运用非常广的元素，本文对于包含这三种元素的装配线平衡问题进行研究，是符合目前企业制造生产实际需求的。

1 随机型混合U型装配线平衡问题的描述与数学模型

1.1 随机型混合U型装配线平衡问题的描述

在定义模型之前，首先假设：（1）优先约束对于所有产品都是一致的（对任一产品，如果作业i与作业j存在优先关系，则对于其他产品亦是如此）；（2）作业在工作站内的分配对所有产品都是一致的（假设作业i被分配到j工作站，则对于所有产品的作业i都被分配到了j工作站）；（3）忽略工作站中操作人员的行走时间。

装配线有N个作业元素，i=1，2，…，N；混合产品的品种数量为M，m=1，2，…，M；工作站数量为J，j=1，2，…，Jmax。设在一个计划期T内，对第m种产品的需求量为Dm，则对M种产品的总需求量第m种产品的需求比平均生产节拍：

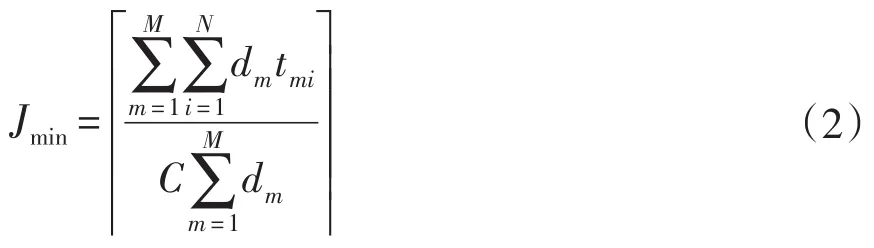
此公式计算的工作站数是最小值。本文描述的是混合产品随机时间作业，在分配作业的时候，由于不同产品在同一作业时间的差异性和随机性的影响，会导致实际所需的工作站数量大于Jmin。例如装配线上有较多作业的平均作业时间较长甚至接近平均节拍，在分配这类作业时对应的工作站内已经分配部分作业，剩余的作业时间不足以分配这类作业，按照作业先后顺序约束，该作业只能分配到下一个工作站中，导致当前工作站的空闲时间很长，装配线所需工作站数增加。同时按照平均负荷来计算工作站数能够满足需求，但由于不同品种产品在少数作业可能存在比较大的差异，致使个别品种产品在差异相对应的工作站的作业时间超出根据计划量得出的平均节拍，在这种情况下也会增加实际的工作站数。对于U型装配线的作业分配，以上两种情况也会对装配线作业分配有一定影响。但相对于传统的直线型装配线，以上情况对U型线影响较小。因为U型装配线可以前向、后向和双向分配，在出现平均作业时间较长的作业时分配方法比较灵活。因此本文在对平衡问题进行算法求解时，会根据作业分配需求对工作站数进行调整，初始值为Jmin，在求解过程中会根据个工作站内的平均负荷和瞬时负荷来对初始值进行修正，下文中提到的Jmax值是修正过程中出现的最大值。

当装配线开始运行后，各工作站的负荷比较均衡的时候，站间的等待和阻塞时间较短，各工作站的利用率较高，生产效率提高。而当其负荷不均衡时产生的结果就会相反。因此工作站的负荷均衡在装配线平衡问题中是非常重要的，本文在考虑最小化工作站数的同时，也把各工作站的负荷均衡设为优化目标。描述为：

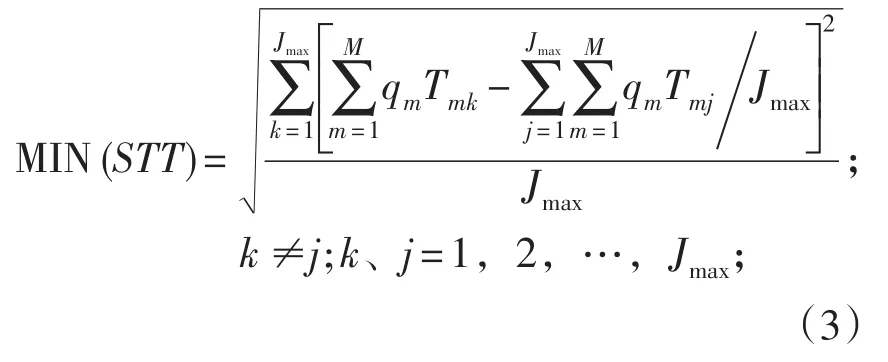
混合产品在同一作业元素上的作业时间可能会存在比较大的差距，这种情况也会使得装配线工作站利用率和生产效率下降，因此本文也把各工作站第m种产品负荷均衡设为优化目标，描述为

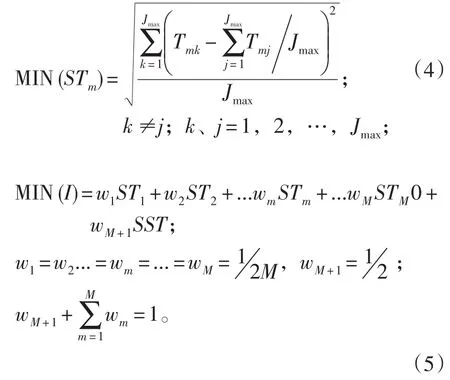
1.2 随机型混合U型装配线平衡问题的数学模型

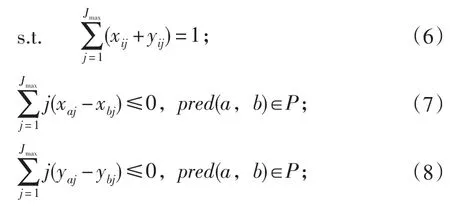
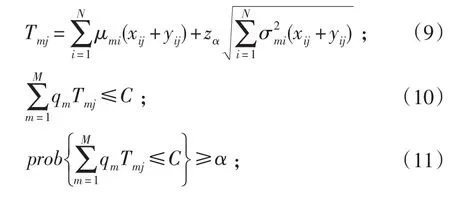
式（1）表示平均生产节拍；式（2）是工作站的初始值；式（3）、（4）、（5）是目标函数；式（6）保证每一个作业元素分配到唯一工作站（xij表示如果作业元素i被前向即U型线前端分配到工作站j，则xij=1，否则xij=0；yij表示如果作业元素i被后向即U型线后端分配到工作站j，则yij= 1，否则yij=0）；式（7）和式（8）保证了作业元素按照U型装配线分配原则进行分配且不违反作业间优先顺序关系，作业元素优先关系集式（9）计算了第m种产品在工作站j内的作业总时间；式（10）确保了每个工作站的平均负荷不超过给定节拍C；式（11）是本文的概率约束模型，α代表U型线上的完工率，zα为标准正态分布的上α分位点，模型代表了在一定完工率α下各工作站的平均负荷不超过给定节拍。

2 随机型混合U型装配线平衡问题的遗传算法求解

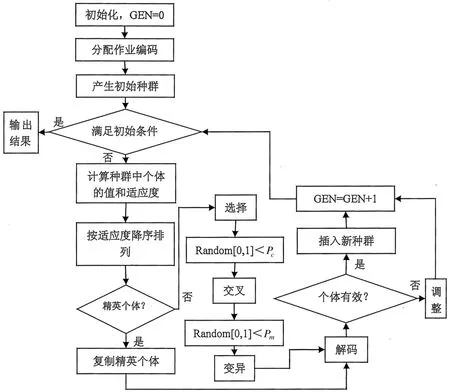
图1 改进的遗传算法流程图（GEN为当前代数，Pc为交叉概率，Pm为变异概率）

装配线平衡问题实际上是作业元素的分配问题，属于组合优化问题。即在满足作业先后顺序条件及各工作站的平均负荷不超过平均节拍这两个约束条件下，将装配线的作业元素分配到装配线上各个工作站中，并使得目标函数最小。遗传算法是解决这类问题的一种有效方法，但是遗传算法在求解这类问题时容易陷入局部最优，因此本文运用一种改进遗传算法以求解随机型混合U型装配线的平衡问题。

2.1 基于序列组合的编码方式

本文采用序列编码方式，按照U型装配线的分配原则将作业元素先后分配到各工作站。如图1所示，每个作业元素对应一个基因位排成一排，当作业元素被全部分配完成后，一排基因位即对应一条基因串即编码的染色体，基因串从左向右的顺序代表了作业元素的分配顺序。解码的过程即按照按照染色体中的基因顺序分配作业元素至各工作站，并满足在给定完工率下分配至各工作站中所有作业元素的时间和不超过给定的节拍。

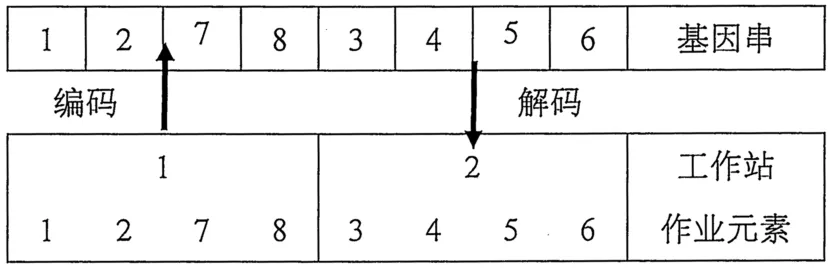
图2 一组基因串编码与解码

2.2 初始种群的产生

初始种群是一组满足约束条件分配后的作业序列组成的个体。即前向与后向或者同时前后向分配作业元素到工作站，同时满足作业优先关系和个工作站总时间不超过给定节拍的约束。随机产生一组可行作业元素序列并按照上述编码方式编码，循环一定次数后形成初始种群，循环的次数即种群的大小（popsize）。初始种群产生的步骤如下。

步骤1 设种群大小计数器size=1。

步骤2 随机产生一个可行解：

（1）设作业元素关系图形成的作业优先矩阵为W，给定节拍C，记初始工作站数l=1，工作站空闲时idle_time=C，记作业分配循环次数。

（2）对矩阵W进行竖列和横行搜索，如第i列全为0，表明i代表的作业没有前序作业；如第j行全为0，则j代表的作业没有后序作业。将没有前序和后序作业的作业元素记录到表A中。当表A为空时，表示作业元素全部分配完毕则程序终止。否则转（3）。

（4）从表B中随机选择一个作业元素i作为最终分配作业元素分配到工作站中，记

（5）更新优先矩阵W，将分配到表B中的作业元素i在优先矩阵中对应的行和列都去掉并转（2）。

步骤3 对步骤2生成的可行解进行编码。

步骤4 size=size+1，如果size≤popsize转向步骤2，否则转步骤5。

步骤5 结束。

2.3 适应度函数设计

本文的目标函数是求最小值，所以适应度函数设计为

2.4 遗传算子选择

2.4.1 选择

选择操作采用最优保存策略和轮盘赌选择相结合的方法。先按照个体对应的适应度值从高到低排序，排位较前的若干个体可以直接复制到下一代种群中，剩余的个体选择轮盘赌法进行筛选。此方法在保存了种群中优良个体的同时也不会降低种群中个体的多样性。

2.4.2 交叉

交叉操作采用单点顺序交叉法，在遗传过程中保留父代中优良作业序列，避免往后可能产生不可行解，提高遗传交叉效率。从保留下来的父代种群中任意选取2个基因串，如图3和4中的基因串ch1与ch2为2条不同的作业分配序列，随机在基因串中选取一个点，即交叉点。如图5所示，在交叉点上将ch1与ch2分成左右两个部分。取ch1的左边部分，并在ch2中将ch1左边部分的基因删除，剩余的基因按照原来的顺序排列。将ch1的左部和以ch2按上述步骤处理后得到的基因位右部，重新组成一个基因串ch1'，同理可得ch2'。ch1'与ch2'的解码结果如图6所示。用产生的后代ch1'和ch2'代替ch1与ch2加入新种群中。

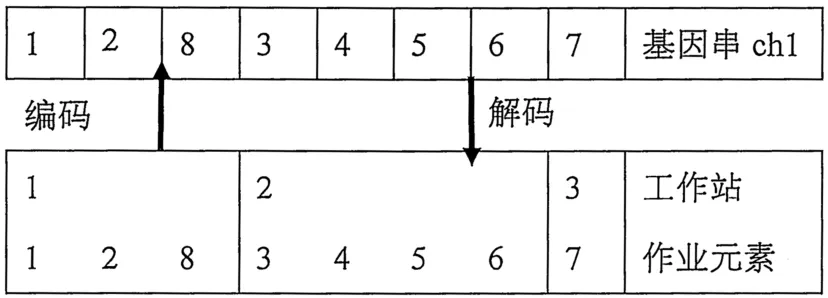
图3 ch1的作业分配方案

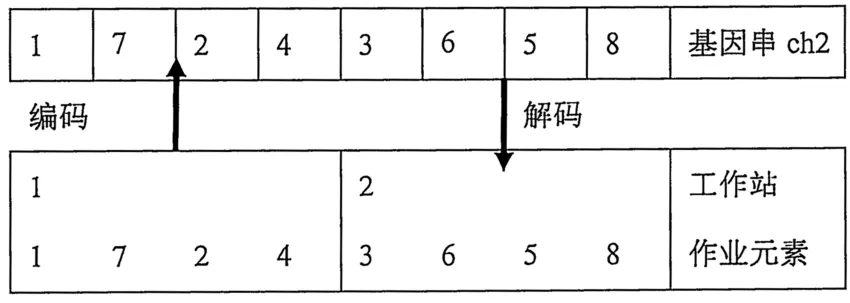
图4 ch2的作业分配方案

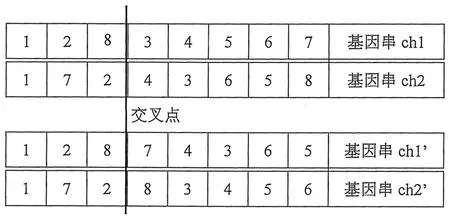
图5 ch1和ch2的单点顺序交叉

图6 ch1'和ch2'的解码过程

2.4.3 变异

按照一定的变异概率Pm，进行变异操作。先在种群中随机选择一个个体，在该个体基串上随机选择两个基因座，对这两个基因座上的基因值以Pm概率进行交换。由于此操作可能会产生无效个体，因此完成操作后需要对变异操作产生的新个体进行有效性检验，对于产生的无效个体，需要再次进行任务分配而成为有效个体为止。

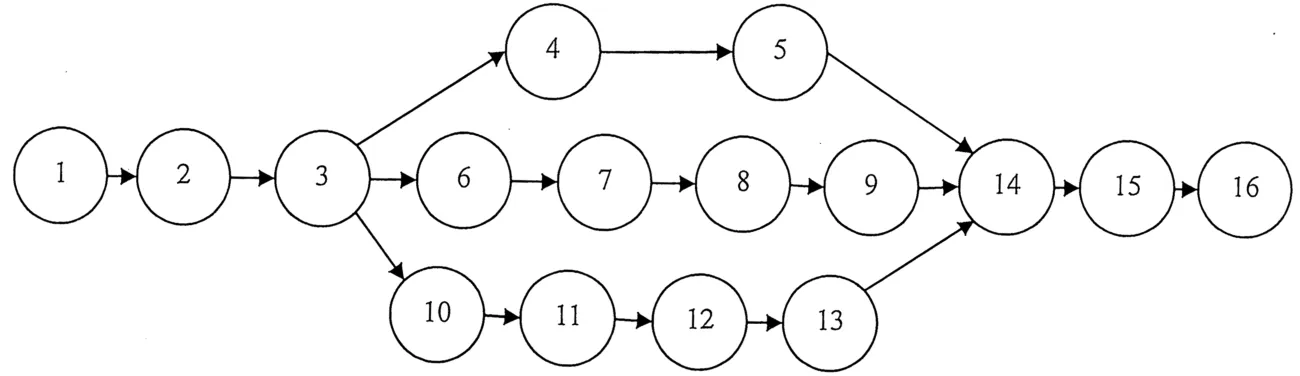
图7 产品1、2、3的联合作业优先图

3 实例分析

如图所述，某类产品的三种型号在某一时期内的计划产量分别为D1=100台，D2=50台，D3=50台。在一个生产循环内，r=50，d1=2台，d2=1台，d3=1台。采用改进后的遗传算法，参数设定为：种群规模为pop_size=60，遗传代数为100，变异概率Pm=0.8，交叉概率Pc=0.08。图7是3种产品的联合作业优先图，表1是三种产品的作业时间表，其中数字代表(μmi，σmi) ，单位是min。

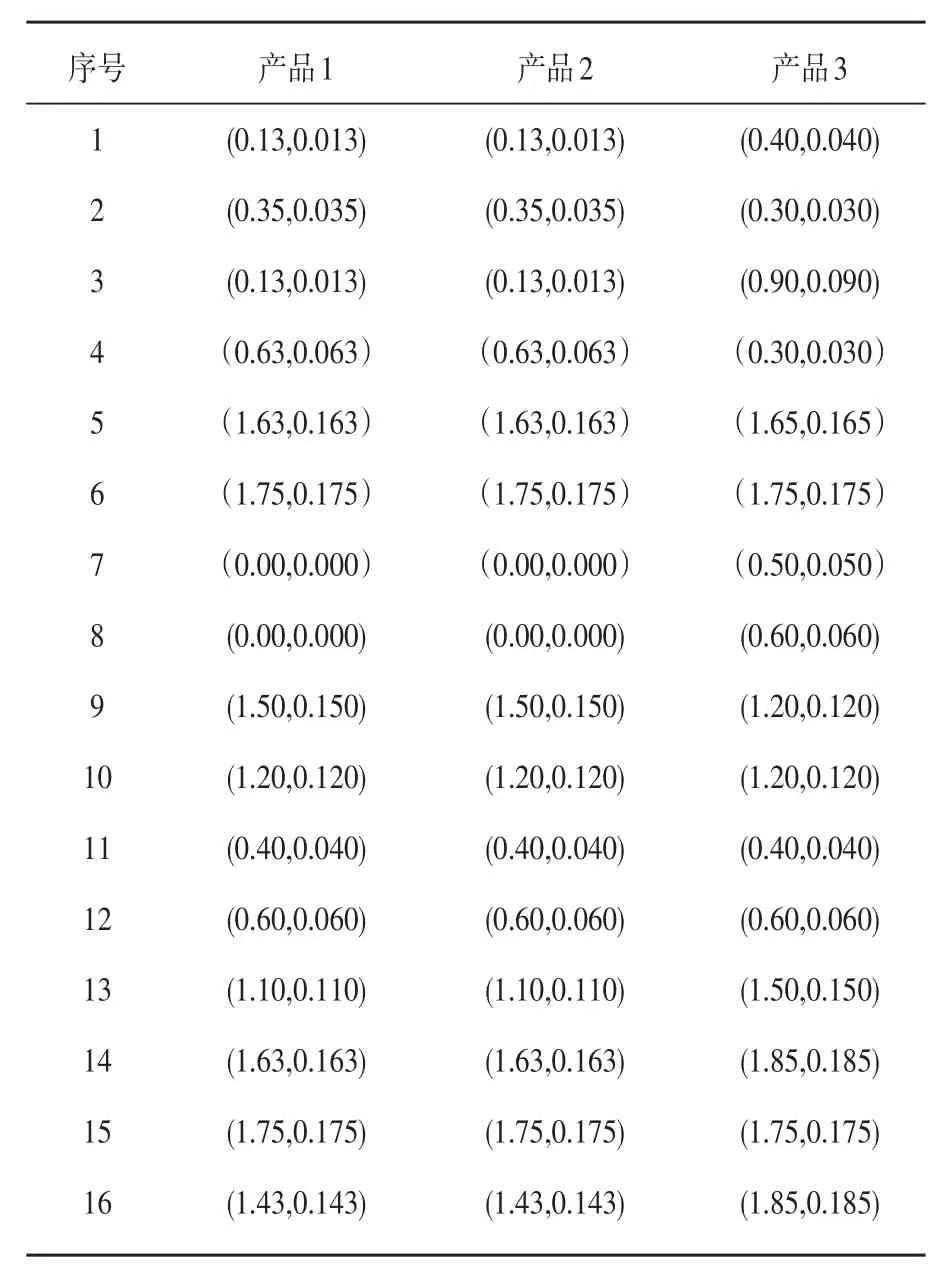
表1 产品1、2、3的作业时间表

由式1可得C=2.2 min（时间利用率设90%），由式2可得Jmin=8（设完工率α=0.95，对应的zα= 1.645），采用上述遗传算法，并对算法编程后，求得的最优解如表2所示。

4 结论

本文针对随机型混合U型装配线平衡问题中作业时间不确定性的问题建立了数学模型，提出了改进的遗传算法，系统地描述了混合产品在U型装配线上的运用。由于约束的增多，当实际情况中产品种类过多时，算法较为复杂，因此针对不同的实际情况需要对其进行系统仿真来辅助算法的运用。其次混合产品的排序也会对工作站负荷产生影响，这些问题将是后续研究的方向。

表2 最优解方案

［1］Salveson M.The assembly line balancing Problem［J］. Journal of Industrial Engineering，1955，6（3）：18-25.

［2］Arcus A.L.COMSOAL—A computer method of sequenc⁃ing operations for assembly lines［J］.International Jour⁃nal of Production Research，1966（4）：259-277.

［3］Miltenburg J，Wijingaard J.The U-line balancing prob⁃lem［J］.Management Science，1994，40（10）：1378-1388.

［4］Sparling D，Miltenburg J.The mixed-model U-line bal⁃ancing problem［J］.International Journal of Production Research，1998（36）：485-501.

［5］Miltenburg J.U-shaped Production lines：A review of theory and practice［J］.International Journal of Produc⁃tion Economics，2001，70（3）：201-214.

［6］Ajenblit D.A，Wainwright R.L.Applying genetic algo⁃rithms to the U-shaped assembly line balancing problem［C］.Proceedings of the 1998 IEEE International Confer⁃ence on Evolutionary Computation，1998：96-101.

［7］ Scholl A， Klein R.ULINO： Optimally balancing U-shaped JIT assembly lines［J］.International Journal of Production Research，1999，37（4）：721-736.

［8］Erel E，Sabuncuoglu I，Aksu B.A.Balancing of U-type assembly systems using simulated annealing［J］.Inter⁃national Journal of Production Research，2001（39）：3003-3015.

［9］Agpak K，Gokcen H.A shortest route formulation of sim⁃ple U-type assembly line balancing problem［J］.Ap⁃plied Mathematical Modeling，2005（29）：373-380.

［10］ ThomopoulosN.T.LineBalancing-sequencingfor Mixed-model Assembly Line［J］.Management Sci⁃ence，1967（14）：859-875.

［11］Roberts S.D，Villa C.D.On a Multi-Product Assembly Line balancing Problem ［J］.AIIE Transactions，1970（2）：361-364.［12］Korkmazel T，Meral S.Bicriteria Sequencing Methods for the Mixed-model Assembly Line in Just-in Time Pro⁃duction Systems［J］.European Journal of Operational Research，2001（131）：188-207.

［13］Joseph B，Ezey M.D，Jacob R.Mixed Model Assembly Line Design in a Make-to-order Environment［J］. Computers&Industrial Engineering， 2002（41）：405-421.

［14］Agpak K，Gokcen H.Assembly Line Balancing：Two Resource Constrained Cases［J］.Production Econom⁃ics，2005（96）：129-140.

［15］ Simaria A.S，Vilarinho P.M.A Genetic Algorithm Based Approach to the Mixed-model Assembly Line Bal⁃ancing Problem of Type II［J］.Computers&Industrial Engineering，2004（47）：391-407.

［16］陆叶，苏平.混合装配线平衡问题的建模与分析［J］.机电产品开发与创新，2007（5）：110-113.

［17］于兆勤.混合型装配线平衡问题的不确定性仿真研究［J］.中国机械工程，2008，19（11）：1297-1302.

［18］Moodie C.L，Young H.H.A heuristic method of assem⁃bly line balancing for assumptions of constant or variable work element times［J］.Journal of Industrial Engineer⁃ing，1965，16（1）：23-29.

［19］Nkasu M.M，Leung K.H.A stochastic approach to as⁃sembly line balancing［J］.International Journal of Pro⁃duction Research，1995，33（4）：975-991.

［20］ Urban T.L.Optimal balancing of U-shaped assembly lines［J］.Management Science， 1998（44）：738-741.

［21］黄卫平，张健，周支立.随机型混合模式装配线平衡问题的集束搜索算法［J］.运筹与管理，2010，19（6）：20-26.

［22］朱华炳，王龙，涂学明，等.随机型混流装配线动态排序问题研究［J］.组合机床与自动化加工技术，2013，11（4）：114-118.

［23］Chiang W.C，Urban T.L.The stochastic U-line balanc⁃ing problem： A heuristic procedure［J］.European Journal of Operational Research，2006，175（3）：1767-1781.

［24］Seyed M.K，Neda M，Masoud R.Mixed model U-line balancing type-1 problem： A new approach［J］. Journal of Manufacturing Systems，2012，31（2）：131-138.

［25］Chun-Hung C，Angappa G，Kin-Chuen H.Genetic search and the U-line balancing problem［J］.Interna⁃tional journal of industrial and systems engineering，2013，14（2）：414-440.

Stochastic Mixed-Model U-Shaped Assembly Line Balancing Problem

ZHENG Chen-ming，DUAN Yi-ting
（Guangdong University of Technology，Guangzhou510006，China）

For the U-shaped assembly line balancing problem of mixed products and stochastic work elements，established the mathematical model and an improved genetic algorithm is put forward.Under the given production tact time and completion rate，with the minimum number of workstations and uniform load between each product as the goal，design the improved genetic algorithm to solve allocation sequence question of the work elements.Finally combine instance to verify the effective.

mixed products；U-line balancing；stochastic；genetic algorithms

TH163

A

1009－9492(2015)10－0027－06

10.3969/j.issn.1009-9492.2015.10.007

郑晨鸣，男，1991年生，江西景德镇人，硕士研究生。研究领域：生产计划与调度（工业工程）。

(编辑：阮 毅)

2015－04－14