基于混沌人工蜂群算法优化的SVM 齿轮故障诊断

刘 霞，张姗姗，胡铭鉴

(1.东北石油大学电气信息工程学院，黑龙江大庆163318; 2.新疆石油勘探设计研究(有限公司)仪信所，新疆克拉玛依834000)

基于混沌人工蜂群算法优化的SVM 齿轮故障诊断

刘 霞1，张姗姗1，胡铭鉴2

(1.东北石油大学电气信息工程学院，黑龙江大庆163318; 2.新疆石油勘探设计研究(有限公司)仪信所，新疆克拉玛依834000)

为克服支持向量机中模型参数的随意选择对分类性能造成的不利影响，提出了基于混沌人工蜂群算法的支持向量机(CABC-SVM:Chaotic Artificial Bee Colony algorithm of Support VectorMachine)参数优化方法。该方法采用Logistic混沌映射初始化种群和锦标赛选择策略，对支持向量机的惩罚因子和核函数参数进行优化时以分类准确率作为适应度函数。通过UCI标准数据集实验证明，CABC具有较强的局部和全局搜索能力，其优化的支持向量机可在很大程度上克服局部极值点，从而获取更高的分类准确率，并有效缩短了搜索时间。将该方法应用于实际齿轮故障诊断中，采用小波相对能量作为特征输入支持向量机，分类准确率达到99.4%，验证了该方法的可行性和有效性。

支持向量机;混沌人工蜂群算法;参数优化;齿轮故障诊断

0 引 言

齿轮作为一种广泛应用于变速传动系统的机械部件，其工作环境具有高速、重负载和强冲击的特点，再加上自身的复杂结构使齿轮发生故障的概率大大增加。因此，以齿轮故障的识别诊断研究作为国内外的研究热点，具有非常重要的现实意义与价值。

近年来，在齿轮故障诊断领域应用较广泛的是基于人工神经网络的模式识别方法［1］，该方法要求具有大量典型的故障样本数据或经验数据进行训练学习，而齿轮的故障数据不能大量获取［2］，使人工神经网络的理论优势在实际应用中难以发挥。针对此问题，Vapnik［3］在统计学习理论基础上提出了一种机器学习方法-支持向量机(SVM:Support Vector Machine)，它可以解决小样本学习、高维及非线性问题，同时可以避免神经网络结构选择和局部极小点问题。由于模型参数(包括惩罚因子C、核函数类型和核函数参数)的选择会严重影响最终的分类结果［4］，因此，在利用SVM进行分类时，需要找到一种方法能准确选择最佳模型参数的方法。人工蜂群(ABC:Artificial Bee Colony)算法是Karaboga［5］提出的一种新的群集智能优化算法，该算法模拟蜜蜂采蜜的智能行为，不同工种的蜜蜂完成各自的收集或共享任务，通过这种信息的整合与分析最终达到寻找最优食物源即最优解的目的。Karaboga等［6，7］通过大量的标准函数测试证明，ABC算法与传统方法相比具有更佳的优化性能，它通过蜜蜂之间的分工合作很好地兼顾了精密搜索已知解域与扩展新解域，从而降低了算法陷入局部最优解的概率。

笔者采用支持向量机作为分类器，利用ABC算法对模型参数进行优化，通过对标准数据集和实测齿轮故障数据的训练及分类测试实验证明，ABC算法能克服局部最优解，在一定程度上加快搜索速度，优化后的SVM具有更高的分类准确率，从而验证了该方法的可行性和有效性。

1 支持向量机分类器

1.1 支持向量机两类分类器

SVM分类的过程就是在空间找到一个满足分类要求的最优分类超平面，该超平面在保证分类正确的基础上，能使两类数据集间的距离最大。将 SVM的学习过程转化为优化问题，设有训练样本集{(xi，yi)，i=1，2，…，l}，输入xiRn，期望输出yi∈{+1，-1}，其中+1，-1分别代表两类的类别标识，则该数据集的分类超平面可描述为wgx+b=0。寻找最优超平面的公式如下

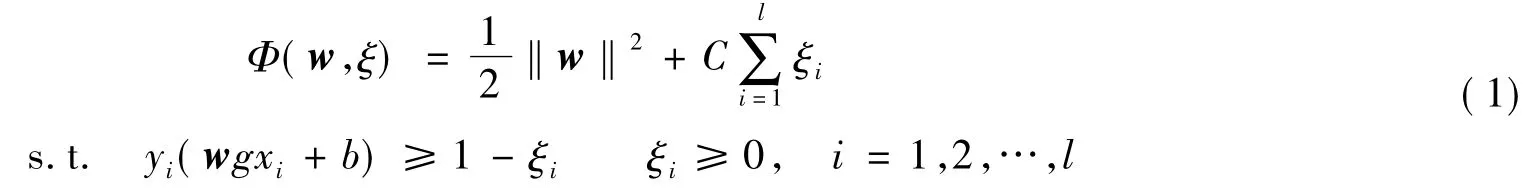
其中w为超平面的法向量;C为错误惩罚因子，它控制对错分样本的惩罚程度，C越大对错误的惩罚越重;ξ为松弛变量，当分类面出现错分时ξi＞0;b∈R为阈值。

采用Lagrange乘子法求解式(1)，将具有线性约束的二次规划问题转化为对应的对偶问题

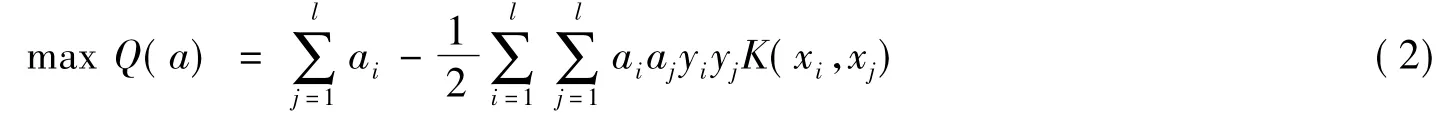
其中K(xi，xj)为核函数。目前常用的核函数主要有多项式核函数、径向基函数、多层感知器和动态核函数等［8，9］。笔者采用径向基核函数，其值受核函数参数σ的影响。

1．2 支持向量机多分类器

支持向量是针对两类问题提出的分类方法，但齿轮的故障类型超过两类，因此，需要研究用支持向量机解决多类的分类问题。多类分类是以二分类为基础的，目前采用的多类分类算法［10］主要有一对一(One Against One)、一对多(One Against All)和有向无环图分类法(Directed Acyclic Graph)等，笔者采用一对一的分类方法。多类分类问题可表述为:给定属于k类的m个训练样本(x1，y1)，…，(xm，ym)，其中xi∈Rn，i=1，…，m，且类别标签yi∈{1，…，k}。

一对一的多分类方法是在每两个类别之间训练产生一个分类器，对于一个k类问题(包含k类训练数据)，将这k类训练数据进行两两组合，一共可构建M=k(k-1)/2个训练集，利用SVM二分类算法分别对这M个训练集进行学习，从而产生M个分类器。测试阶段的类别判断采用投票决策法(Voting Strategy)［11］，用所有的分类器对样本xt进行分类，在第i类和第j类之间分类时，若该分类器判断xt属于i类，则i类的票数加1，否则j类的票数加1。最后将待分类的样本xt归为得票数最多的那类。

综上可知，无论是两类分类器还是多类分类器，要使支持向量机获得最佳分类性能，必须寻找最优的惩罚因子C和核函数参数σ。

2 引入混沌机制的人工蜂群算法

2．1 ABC算法优化原理

ABC算法模拟实际蜜蜂采蜜机制处理函数的优化问题，ABC分为3部分:引领蜂、跟随蜂和侦查蜂。在每次循环中，首先是引领蜂搜索，从一个随机产生的初始种群开始，在适应度值较优的一半个体周围进行搜索，采用一对一优胜劣汰的竞争方式选择并保留较优个体;然后跟随蜂搜索，利用轮盘赌的选择策略选择较优个体，并在其周围进行贪婪搜索产生另一半个体;最后侦查蜂搜索，如某个食物源被放弃，则产生侦查蜂，寻找新的食物源。

ABC算法在求解最优问题时，食物源的位置代表优化问题的可能解，每个食物源的花蜜量代表每个解得的适应度值。一个非线性函数最小值问题可表示为min f(X)，XL≤X≤XU，其中XL和XU分别是变量X取值的上界和下界，X=(x1，x2，x3，…，xn)，n为变量的维数。利用ABC求解该最优问题的具体过程如下。

2．1．1 种群初始化

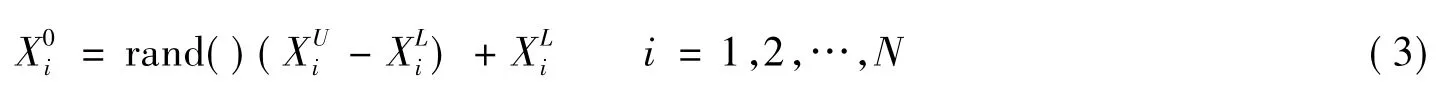
在取值范围内按公式随机产生一个包含N个个体的初始种群。其中X0i表示初始种群中的第i个个体，其维数n为优化参数的个数;rand()表示在区间［0，1］上产生的随机数。

对初始种群的一半计算适应度值及可行解的质量，记录目前质量最好的解。

2．1．2 引领蜂阶段

引领蜂的数量等于食物源N的一半，即N/2，表示初始种群中适应度值较优的一半个体，与食物源的位置相对应。引领蜂随机选取食物源进行交叉搜索，按公式

对食物源进行更新，即产生一个新解。其中k∈{1，2，…，N/2}，j∈{1，2，…，n}，且k≠i，φij为［-1，1］之间的随机数。在计算新解的适应度值时，如果新解的适应度优于旧解，则用新解代替旧解，反之，保留旧解。

2．1．3 跟随蜂阶段

跟随蜂的数量跟引领蜂的数量相等，也是N/2。跟随蜂根据引领蜂搜索的信息，按照与适应度相关的概率选择食物源的位置，即解得位置，并像引领蜂一样按式(4)对食物源进行更新，若新解的适应度值优于旧解，用新解替代旧解;反之保留旧解。跟随蜂选择食物源的概率

其中fi为第i个解的适应度值。

2．1．4 侦查蜂阶段

经过引领蜂与跟随蜂的搜索后得到与初始种群相同大小的新种群，为避免随着种群的进化出现种群多样性丧失过多的问题，人工蜂群算法模拟侦查蜂搜索潜在蜜源的生理行为，提出了一种特有的搜索方式-侦查蜂搜索。如果某个体(解)连续很多代没有变化，与之对应的个体变异成侦查蜂，则按式(3)搜索产生新个体，计算新个体的适应度值并与原个体比较，依然采用优胜劣汰的竞争机制择优并保留个体。

经过引领蜂、跟随蜂和侦查蜂3个阶段的搜索后，整个种群进化到下一代，这个过程反复循环直至达到最大迭代次数或最终误差达到预定的范围内，结束算法。

人工蜂群算法原理简单、参数少、容易实现，并且已被证明是一种优秀的全局优化算法，但仍存在不足，如易早熟收敛，进化后期寻优速度慢等。为了克服这些不足，笔者对人工蜂群算法做了一些改进。

2．2 混沌人工蜂群算法(CABC:Chaotic Artificial Bee Colony)

2.2.1 混沌初始化

混沌看似混乱却有精致的内在结构，是非线性系统中特有并普遍存在的一种现象。随机性、遍历性和规律性是混沌最典型的特点，使其能按照自身的某一“规律”不重复地遍历给定范围内的所有状态。将混沌思想引入到人工蜂群算法中，可在一定程度上防止算法陷入局部最优并加快进化速度。笔者采用Logistic混沌映射初始化种群。Logistic混沌映射的方程如下

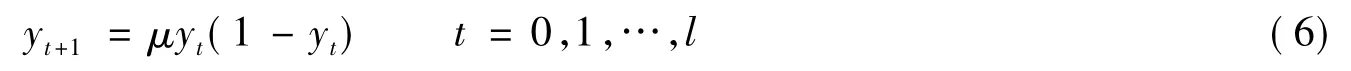
其中yt∈(0，1);l是混沌序列的迭代次数;μ是混沌序列的控制参数，取值范围为［3．75，4］。

具体过程如下:

1)设置混沌序列的迭代次数l=100，控制参数μ=4、i=1;

2)随机产生混沌序列的初始向量y0=(y01，y02，…，y0D)，其中D为优化问题的维数，y0中不能包含0．25、0．5和0．75这3个数值。

3)根据混沌方程循环迭代，产生混沌向量yl=(yl1，yl2，…，ylD);

5)计算i=i+1，如果i大于种群个数N，则结束，否则返回2)继续循环。

经过以上步骤就可产生N个初始种群。

2．2．2 锦标赛选择策略

传统的ABC算法中跟随蜂所采用的选择策略称之为按比例的适应度选择策略(Proportional Fitness Selection)。使用该选择策略，在运行早期可以很顺利地选择出具有较优适应度值的个体，淘汰适应度较差的个体;但当种群进化到一定程度后个体的适应度值越来越相近，导致个体被选择的概率也越来越相近，从而导致很难选择出优秀个体，使搜索过程停滞。因此，这种比例选择策略容易使种群过分丧失多样性，从而导致算法陷入早熟。为了避免早熟现象，提高ABC算法的全局收敛性和搜索效率，笔者采用了锦标赛选择策略。

锦标赛是基于局部竞争机制的选择过程，基本思想是在整个群体中随机选择k个个体进行比较，选择适应值较优的个体，这里的参数k称为竞赛规模，默认取2。在ABC算法中，将第t代某个个体的适应度值与其他所有个体两两进行比较，对适应度值较优的个体授予1分，对每个个体重复这一过程，个体得分越高表示个体越优秀，被选择的概率越大。这种方式根据种群个体间适应度值的关系进行选择，与个体的适应度值无关，因此，对适应值的正负没有要求，从而提高优秀个体被选择的概率，在一定程度上避免了比例选择策略可能出现的过早收敛和停滞现象。

2.3 实验仿真与结果分析

为验证CABC的有效性，采用函数优化领域常用的4个标准测试函数进行测试。ABC算法的控制参数设置如下:种群个数(食物源数量)N设为20，最大迭代次数Imax设为2 000，个体最大更新次数Lmax设为100，表1描述了测试函数的函数形式、定义域以及最优值。图1～图4分别给出了对4个函数的测试结果。

表1 标准测试函数描述Tab.1 Description of the standard test functions

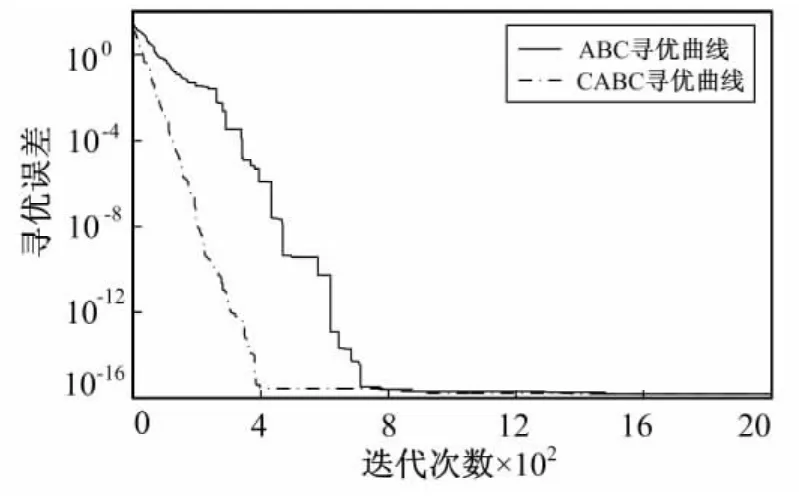
图1 函数Sphere的测试结果Fig.1 Test results of Sphere test function

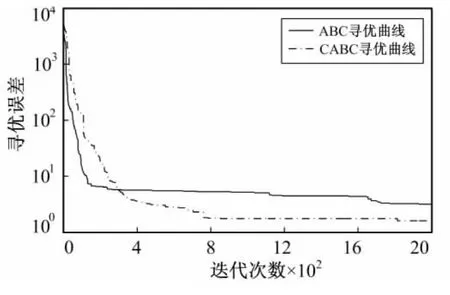
图2 函数Rosenbrock的测试结果Fig.2 Test results of Rosenbrock test function

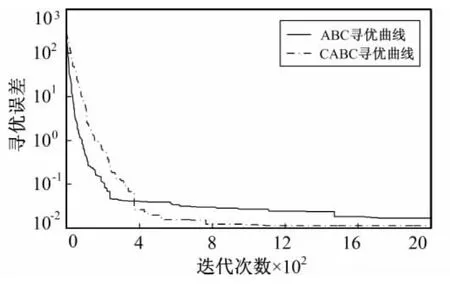
图3 函数Griewank的测试结果Fig.3 Test results of Griewank test function

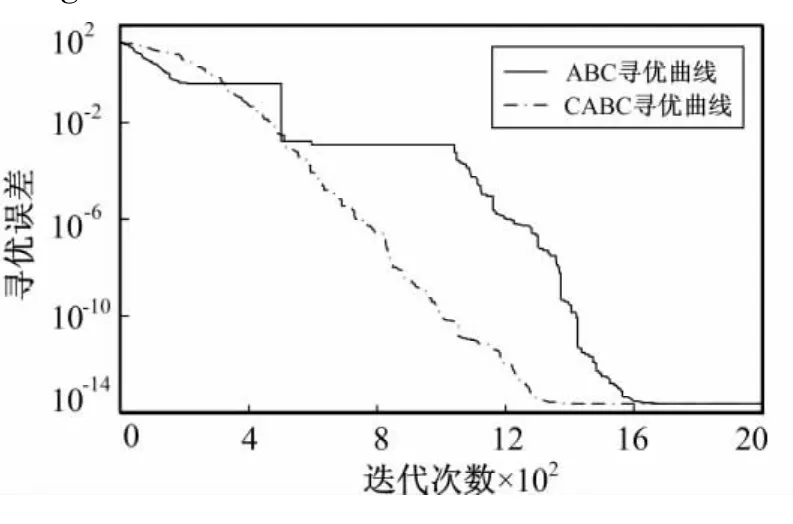
图4 函数Ackley的测试结果Fig.4 Test results of Ackley test function

从图1和图4可以看出，CABC算法的收敛性优于ABC算法，在函数Sphere的测试中，ABC算法在迭代次数达到800时基本收敛，CABC算法在迭代次数达到400时基本收敛;在函数Ackley的测试中，ABC算法在迭代次数达到1 600时基本收敛，CABC算法在迭代次数达到1 300时基本收敛，而且从整个曲线的走势看，CABC算法的曲线比较光滑，同时验证了CABC算法能克服局部最优解。从图2和图3中对函数Rosenbrock和Griewank的寻优结果可以看出，CABC算法的寻优误差明显比ABC算法小，验证了CABC算法具有更高的寻优精度。

3 基于CABC优化的支持向量机分类器

3.1 CABC算法优化支持向量机的算法流程

1)算法初始化。设定最大迭代次数Imax、种群个数N、维数D(由于需要优化的参数有两个，所以D=2)、个体最大更新次数Lmax、惩罚因子C和核函数参数σ的最大值分别为(Cmax，σmax)，其最小值分别为(Cmin，σmin)。

利用式(7)产生混沌初始种群(即惩罚因子C和核函数参数σ的初值)，将惩罚因子C和核函数参数σ的初值写入SVM模型，并对训练样本进行训练分类，准确率即为ABC的适应度值，记录最好的适应度值和对应的参数值。

2)引领蜂按式(4)搜索更新，计算适应度值，即SVM对训练样本的分类准确率，若新食物源的适应度值优于搜索前，则代替先前的食物源。

3)跟随蜂根据锦标赛选择策略选择食物源，并按式(4)在食物源附近搜索新的食物源。计算新食物源的适应度值，若新食物源的适应度值优于搜索前，则代替先前的食物源。

4)判断是否存在需要放弃的食物源。如果某个食物源经Lmax次循环后没有改变，则放弃该食物源，同时对应的引领蜂变异为侦查蜂，按式(7)产生新的食物源。

5)迭代次数I=I+1，若I达到最大迭代次数Imax或分类准确率达到设定精度，则结束算法，输出最优值;否则返回步骤2)。

3．2 仿真实验

为了验证笔者算法的有效性和优越性，采用UCI(University of California，Irvine)数据库(http://archi ve.ics.uci.edu/m l/)中的3个具有代表性的数据集Heart、Iris和Wine进行训练和分类实验，数据集详细信息如表2所示。ABC算法的控制参数设置如下:食物源数量N设为20，最大迭代次数Imax设为1 000，个体最大更新次数Lmax设为50，惩罚因子的搜索范围设为［0．1，100］，核函数参数的搜索范围设为［0．01，1 000］。

将传统SVM、ABC-SVM和CABC-SVM的分类正确率进行比较，比较结果如表3所示。由实验结果可以看出，ABC算法能兼顾全局最优解和局部最优解的搜索，对SVM进行参数优化后，可得到更高的分类正确率，而CABC算法能进一步提高支持向量机的分类准确率。

3种算法进行3次试验后得到的平均运行时间如表4所示。从表4中的数据可看出，对支持向量机进行参数优化，由于算法的复杂性增加从而使运行时间增加，但是CABC优化的SVM在一定程度上缩短了运行时间，与传统ABC优化的SVM比较表现出更好的收敛性，有效地降低了搜索运行时间。

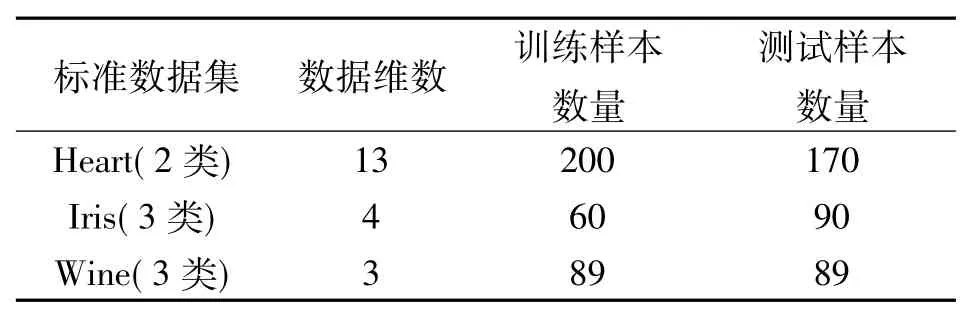
表2 测试数据集信息Tab.2 Instruction of UCIdatasets

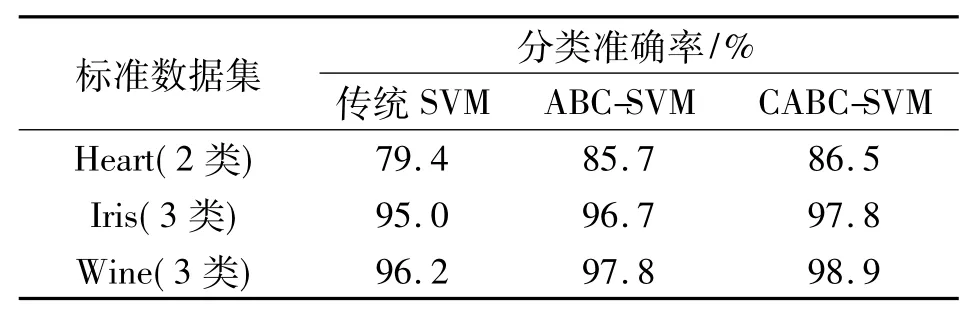
表3 3种算法的分类测试结果Tab.3 The classification test results of three algorithm

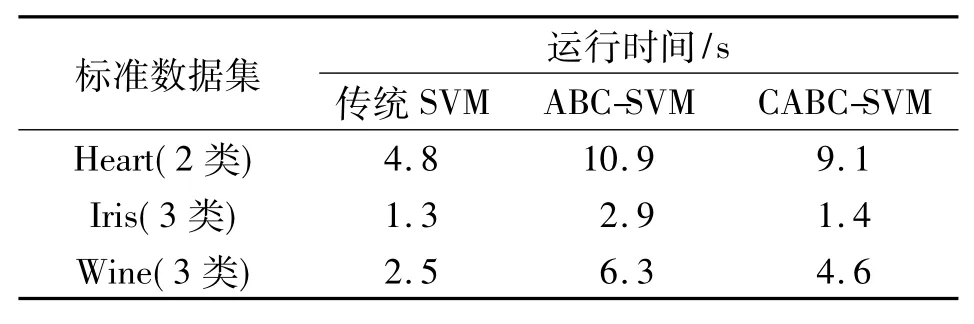
表4 3种算法的运行时间对比Tab.4 Running time comparison of three algorithms

4 齿轮故障诊断

4.1 实验数据采集

该课题使用实验室的旋转机械振动及故障模拟实验平台QPZZ-Ⅱ进行齿轮振动信号采集。采用材质为S45C的齿轮进行实验测量，其大齿轮模数为2，齿数为75;小齿轮模数为2，齿数为55。采用加速度传感器采集正常、断齿、裂痕、磨损4种状态下的齿轮振动数据，采样率为10 Hz;齿轮转速为1 200 r/min。提取每种状态下原始样本各60组，每组样本采样点数为8 192。

4.2 齿轮振动信号的特征提取

小波变换是20世纪80年代中期发展起来的一种多尺度信号分析方法，它将信号分解到不同尺度的空间进行分析处理，然后再根据需要进行信号重构，具有较好的时频局部化特性，因此非常适合对齿轮故障信号非线性、非平稳的复杂信号进行分析与特征提取。

笔者采用信号各频段的相对小波能量作为故障信号的特征进行提取，具体过程如下。

将离散时间信号f(t)进行J层离散小波变换分解，得到低频近似分量系数AJ和高频细节系数Dj，j=1，2，…，J，总的小波能量表达式为

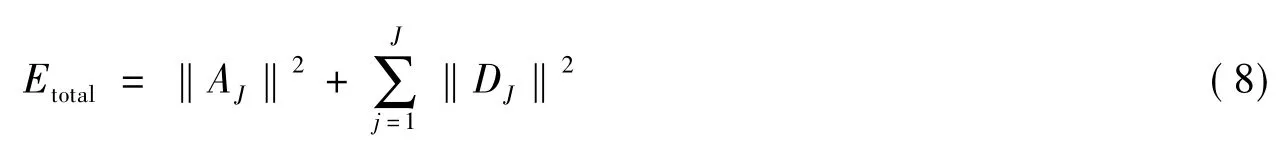
简化公式，将AJ表示为DJ+1，则式(8)表示为

相对小波能量表示为

表5中为4种状态下齿轮振动信号不同频段上的相对小波能量。

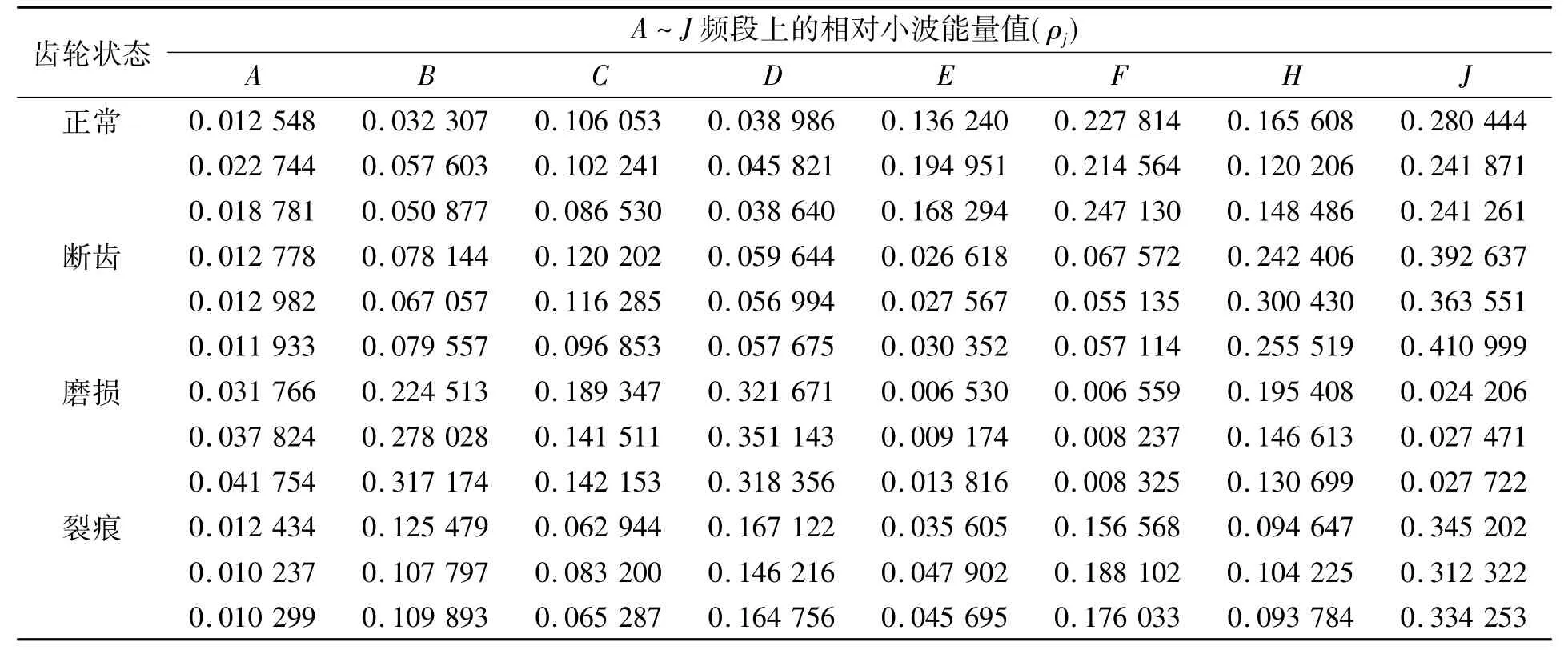
表5 4种状态下齿轮振动信号不同频段上的相对小波能量Tab.5 The relative wavelet energy on different frequency bands of gear vibration signal in four state

4.3 齿轮故障诊断对比实验

为验证笔者算法的实际应用价值，将每种状态下的20组原始样本作为训练样本，另外的40组作为测试样本。按照4.2节的方法对训练样本进行特征提取构成特征向量，并将特征向量进行归一化处理输入支持向量机进行训练。利用CABC算法对支持向量机的惩罚因子C和核函数参数σ进行优化，用训练好的支持向量机对测试样本进行分类测试。传统SVM、ABC-SVM和CABC-SVM3种算法的分类结果如表6～表8所示。由表6可知，传统SVM的分类正确率为98.1%，齿轮断齿状态的40个测试样本中有1个样本分类错误、齿轮裂痕状态的40个测试样本中有2个样本分类错误;由表7可知，ABC-SVM的分类正确率为98.8%，齿轮断齿和裂痕状态的40个测试样本中各有1个样本分类错误;由表8可知，CABC-SVM的分类正确率为99.4%，只有齿轮裂痕状态的40个测试样本中有1个样本分类错误。实验结果证明，基于CABC算法优化的支持向量机能准确地诊断旋转机械的齿轮故障，识别率更高，可靠性更好。

表6 传统SVM算法分类测试结果Tab.6 Classification test results of the traditional SVM algorithm

表7 ABC-SVM算法分类测试结果Tab.7 Classification test results of ABC-SVM algorithm

表8 CABC-SVM算法分类测试结果Tab.8 Classification test results of CABC-SVM algorithm

5 结 语

针对齿轮故障数据难以大量获取的实际问题，笔者采用支持向量机对齿轮故障进行诊断，由于支持向量机的模型参数选择对其分类性能影响巨大，提出了基于混沌人工蜂群算法的支持向量机参数优化方法。通过对UCI标准数据集的分类实验证明，混沌人工蜂群算法在一定程度上克服早熟收敛和寻优速度较慢的问题，其优化后的支持向量机(CABC-SVM)能获得更高的分类正确率和更快的搜索速度。将该方法应用于实测齿轮数据，采用小波相对能量作为齿轮信号特征，与SVM和ABC-SVM的分类结果相比，CABC-SVM具有更高的分类正确率，证明该方法具有重要的工程应用价值。

［1］李佳，礼宾，王梦卿.基于神经网络的齿轮故障诊断专家系统［J］.机械传动，2007，31(5):81-83. LI Jia，LI Bin，WANG Mengqing.Expert System of Gear's Fault Diagnosis Based on Neural Network［J］.Mechanical Transmission，2007，31(5):81-83.

［2］成钰龙，程刚.基于特征信息融合的离散小波SVM齿轮故障诊断方法研究［J］.组合机床与自动化加工技术，2012(8):70-73. CHENG Yulong，CHENG Gang.Based on the Characteristics of the Information Fusion of Discrete Wavelet SVM Gear Fault Diagnosis Method Research［J］.Combination Machine Tools and Automatic Processing Technology，2012(8):70-73.

［3］VAPNIK V N.Statistical Learing Theory［M］.Berlin:Springer-Verlag，1988:123-167.

［4］SHAO Jun，LIU Junhua，QIAO Xueguang，etal.Temperature Compensation of FBG Sensor Based on Support Vector Machine［J］.Journal of Optoelectronics Laser，2010，21(6):803-807.

［5］KARABOGA D.An Idea Based on Honey Bee Swarm for Numerical Optimization［R］.Kayseri:Erciyes University，2005.

［6］KARABOGA D，BASTURK B.A Powerful and Efficient Algorithm for Numerical Function Optimization:Artificial Bee Colony (ABC)Algorithm［J］.Journal of Global Optimization，2007，39(3):459-471.

［7］KARABOGA D，BASTURK B.A Comparative Study of Artificial Bee Colony Algorithm［J］.Applied Mathematics and Computation，2009，214(1):108-132.

［8］王霞，王占岐，金贵，等.基于核函数支持向量回归机的耕地面积预测［J］.农业工程学报，2014，3(4):204-211. WANG Xia，WANG Zhanqi，JIN Gui，etal.Land Reserve Prediction Using Different Kernel Based Support Vector Regression［J］.Transactions of the Chinese Society of Agricultural Engineering，2014，3(4):204-211.

［9］宋晖，薛云，张良均.基于SVM分类问题的核函数选择仿真研究［J］.计算机与现代化，2011(8):133-136. SONG Hui，XUE Yun，ZHANG Liangjun.Research on Kernel Function Selection Simulation Based on SVM Classification［J］.Computer and Modernization，2011(8):133-136.

［10］聂盼盼，臧洌，刘雷雷.基于对支持向量机的多类分类算法在入侵检测中的应用［J］.计算机应用，2013，33(2): 426-429.NIE Panpan，ZANG Li，LIU Leilei.Application ofMulti-Class Classification Algorithm Based on Twin Support Vector Machine in Intrusion Detection［J］.Journal of Computer Applications，2013，33(2):426-429.

［11］段江涛，李凌均，张周锁，等.基于支持向量机的机械系统多故障分类方法 ［J］.农业机械学报，2004，35(4):144-147. DUAN Jiangtao，LI Lingjun，ZHANG Zhousuo，et al.Application of Support Vector Machine in Multi-Fault Classification of Mechanical System［J］.Transactions of the Chinese Society for Agricultural Machinery，2004，35(4):144-147.

(责任编辑:何桂华)

SVM Optimization Based on Chaotic Artificial Colony Algorithm Gear Fault Diagnosis

LIU Xia1，ZHANG Shanshan1，HU Mingjian2

(1.Electrical Information Engineering Institute，Northeast Petroleum University，Daqing 163318，China; 2.Instrument and Signal Institute，Xinjiang Design Institute，China Petroleum Engineering(Company Limited)，Karamay 834000，China)

In order to overcome the adverse effects on the performance of classification of SVM(Support Vector Machine)model parameters in the random selection，based on chaotic CABC-SVM(Artificial Bee Colony Algorithm of Support Vector Machine)parameters optimization method is proposed.CABC algorithm uses the Logistic chaoticmapping initialization population and tournament selection strategy，further improves the artificial bee colony algorithm convergence speed and optimization precision，the classification accuracy as the fitness function when using the algorithm of penalty factor and kernel function parameters of SVM was optimized.UCI standard data sets experiments show that CABC algorithm has strong local and global search ability，the optimization of SVM can largely overcome local extremum points to obtain a higher classification accuracy，and can effectively shorten the search time.The method was applied to actual gear fault diagnosis，energy wavelet was used as the feature input SVM，classification accuracy rate reached 99.4%，verified the feasibility and effectiveness of the improved method in this paper.

support vector machine(SVM);chaotic artificial bee colony(CABC)algorithm;parameter optimization;gear fault diagnosis

TP311

A

1671-5896(2015)04-0476-09

2015-01-30

黑龙江省自然科学基金资助项目(F201404)

刘霞(1970— )，女，黑龙江大庆人，东北石油大学教授，硕士生导师，主要从事信号处理研究，(Tel)86-15845989728 (E-mail)liuxia2k@163.com。