改进的神经网络观测器在非线性系统中的应用

姜寅令，李艳辉，王海星

(东北石油大学电气信息工程学院，黑龙江大庆163318)

改进的神经网络观测器在非线性系统中的应用

姜寅令，李艳辉，王海星

(东北石油大学电气信息工程学院，黑龙江大庆163318)

为降低非线性观测器对模型精度的依赖性，提出一种非传统的神经网络观测器设计方法。该神经网络为三层前馈网络，采用带修正项的误差反传算法进行训练，以保证控制的精度和权值有界，利用神经网络识别系统的非线性部分，并结合传统的龙伯格观测器重构系统状态;利用Lyapunov直接法保证基于权值误差的非观测器的稳定性，并将该观测器应用于机器人轨迹跟踪控制中。仿真结果表明，该方法解决了模型不确定系统状态观测问题，适用于模型精度较低的非线性系统。

神经网络观测器;非线性系统;机器人

0 引 言

近几十年，龙伯格观测器与卡尔曼滤波器一直是传统线性观测器的代表［1-3］，但这种局部线性化模型是有缺陷的，即工作满意度区间较小，局限于操作点附近。因此，传统的非线性观测器得到迅速发展，如鲁棒观测器［4，5］和高增益观测器［6］等。然而传统的非线性观测器的建立较为复杂且对系统模型的精确性要求较高。笔者在非线性系统多层前馈神经网络观测器的基础上［7，8］对其进行改进，采用带线性滤波器的sigmoid活化函数，增强其抗干扰能力。为保证状态观测器的稳定性，参考文献［9，10］选择了带修正项的误差反传算法进行训练以保证控制的精度和权值的有界，并减少了稳定的限制条件，使系统稳定的设计参数选择余地增大。

1 问题描述

考虑如下MIMO非线性系统

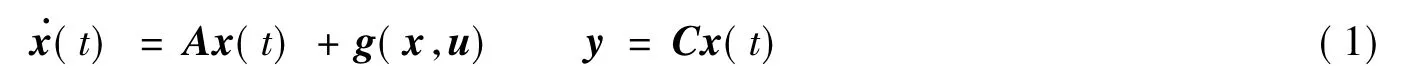
做如下定义。

定义1 V为输入层至隐层的权阵，W为隐层至输出层的权阵，且， WM，VM分别为相应权值上界。

设计神经网络观测器，使其能准确估计系统状态，且观测误差系统渐进稳定。

2 神经网络状态观测器的设计

系统的非线性部分g(x，u)采用神经网络进行估计，可用理想权值表示为

g(x，u)的估计表示为

选择龙伯格形式的神经网络状态观测器的形式［11］

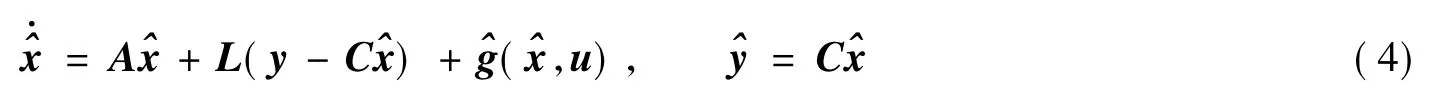
其中L是状态观测器的增益。

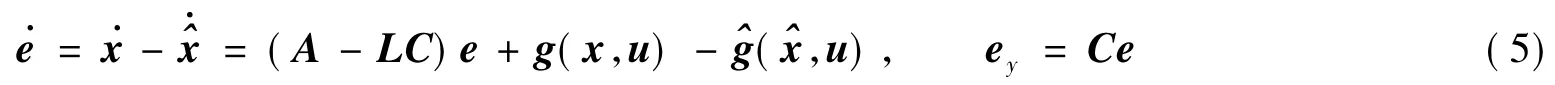
ey表示输出误差向量，对式(5)取拉氏变换，得

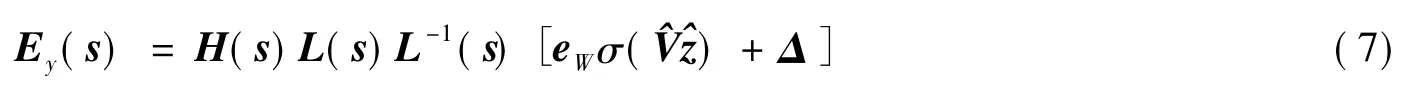
3 稳定性分析

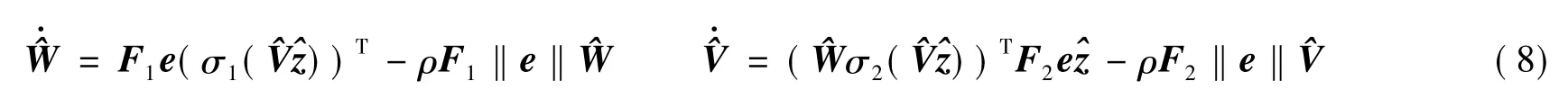
则系统的状态误差e一致最终有界，且神经网络权值估计误差eW、eV和系统状态有界。其中ρ为大于零的常数，F1，F2为正定对称矩阵，。

证明 选取Lyapunov函数

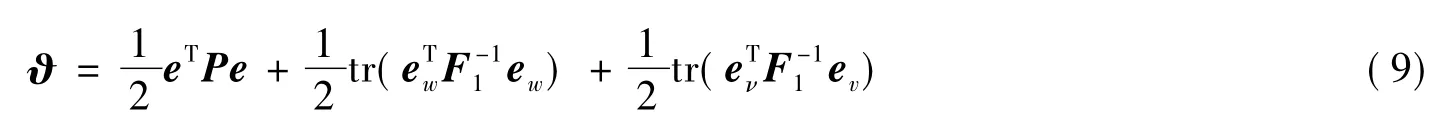
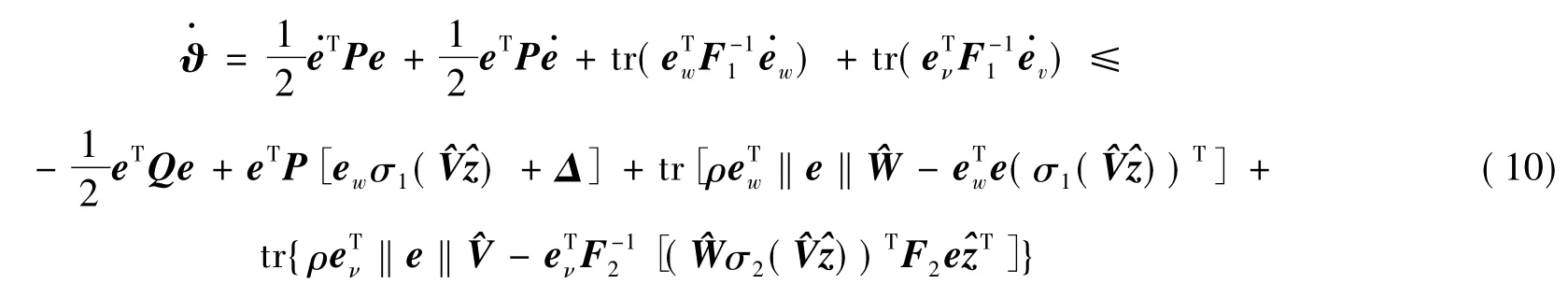
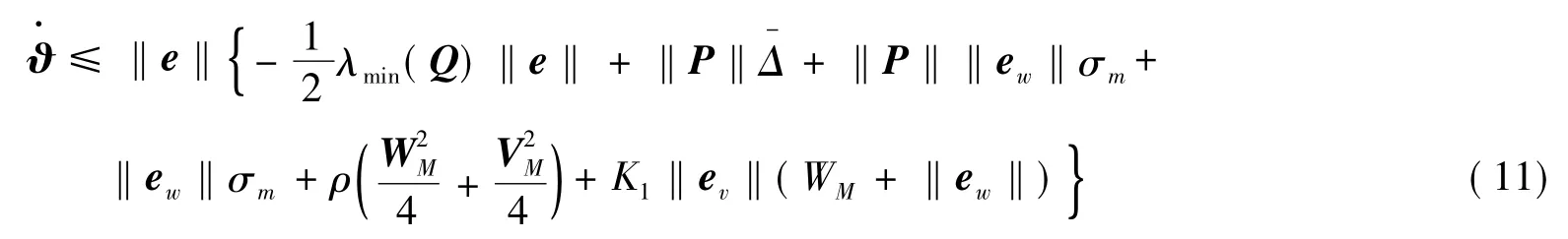
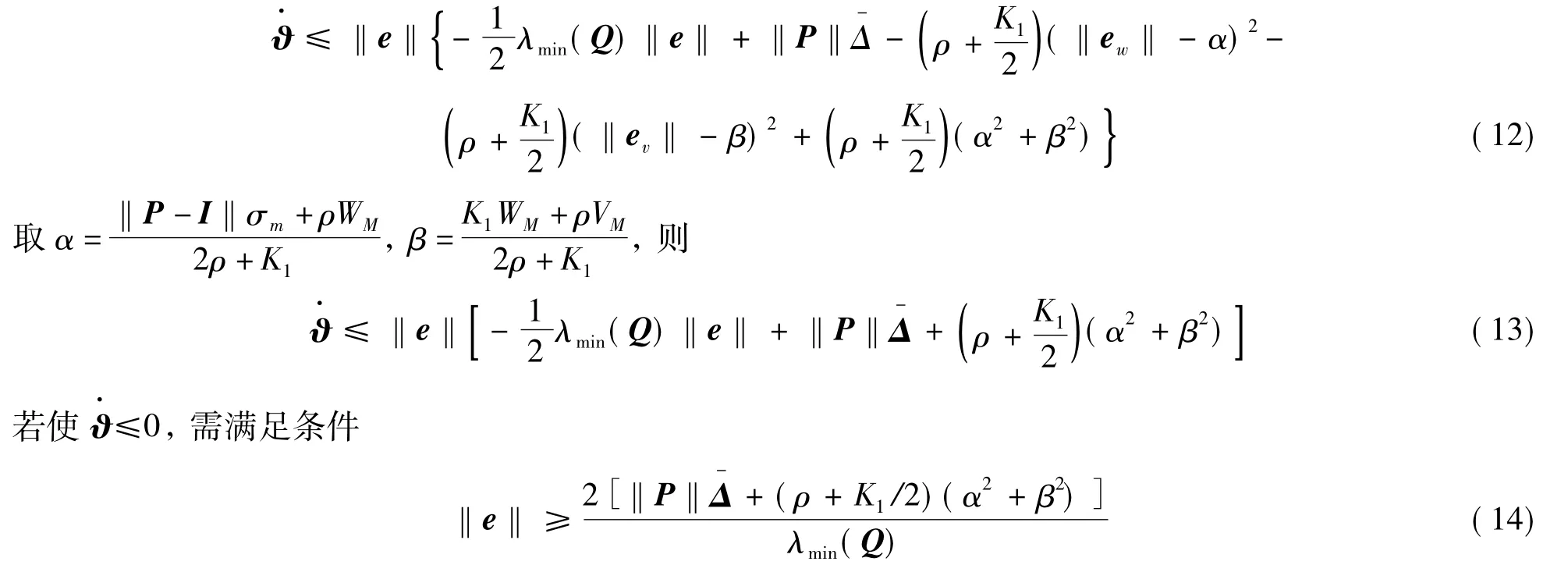
由式(14)可得系统的状态误差e有一致最终有界，且神经网络权值估计误差eW和eV一致最终有界。

4 系统的收敛性分析

为了保证系统状态有界，以下进行系统状态x的收敛性分析。

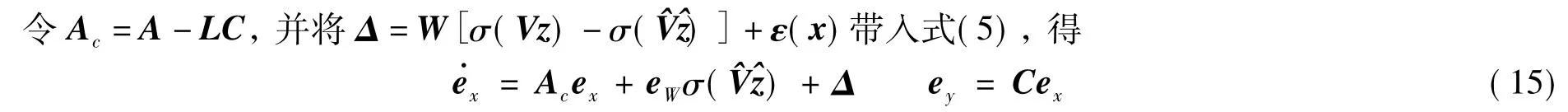
式(16)两边乘e-Act后再积分，得

所以，非齐次状态方程的解为

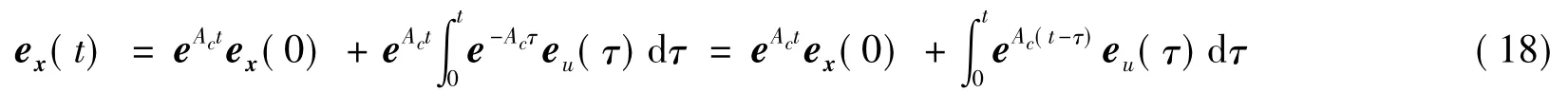
其中

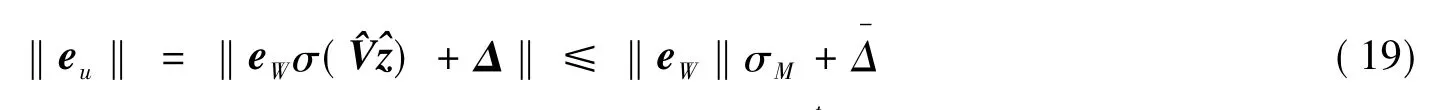
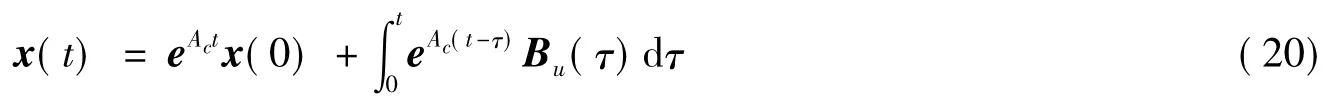
5 仿真实例

考虑二关节刚性机器人模型为仿真对象［12］，根据式(1)，该模型可以表示为

选取观测器参数如下

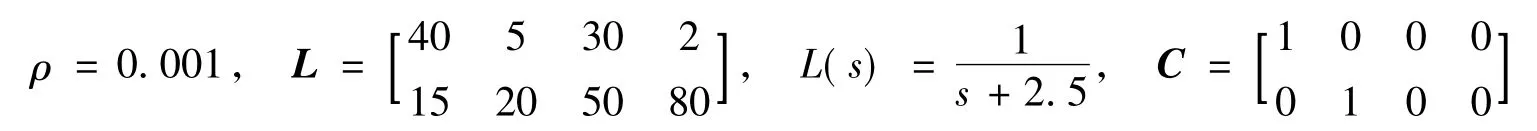
状态观测结果如图1～图4所示。

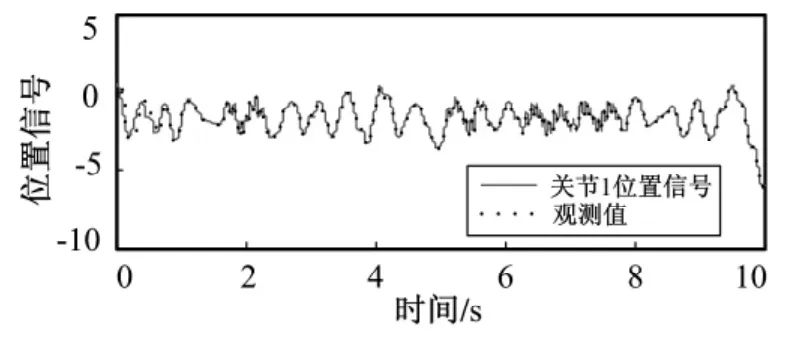
图1 关节1的位置信号及观测值Fig.1 Position signal of q1and observer value

图2 关节2的位置信号及观测值Fig.2 Position signal of q2and the observer value

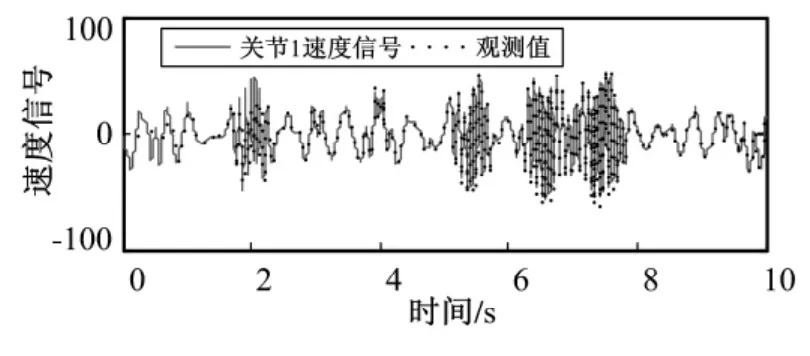
图3 关节1的速度信号及观测值Fig.3 Speed signal of˙q1and observer value

图4 关节2的速度信号及观测值Fig.4 Speed signal of˙q2and observer value

上述仿真未加控制器，输入信号为正弦波信号。从仿真模型可以看出，将传统机械臂建模的哥氏力项、惯性力项及干扰等非线性项大大简化，对模型精确度要求大大降低。

6 结 语

笔者设计的神经网络观测器，采用神经网络估计系统的不确定部分后与传统的龙伯格观测器相结合，实现状态估计，降低了对模型精度的依赖性，是对传统非线性观测器的改进。仿真结果表明，该观测器可精确地估计关节的位置和速度信号，对模型不确定系统状态观测问题提供了解决办法。

［1］祝晓辉，李颖晖，陈亚滨.基于非线性状态观测器的永磁同步电动机无位置传感器矢量控制［J］.电工技术学报，2010，25(1):50-57. ZHU Xiaohui，LI Yinghui，CHEN Yabin.Sensorless Vector Control for PMSM Based on Nonlinear State Observer［J］.Transactions of China Electrotechnical Society，2010，25(1):50-57.

［2］LIBaibing.A Non-Gaussian Kalman Filter with Application to the Estimation of Vehicular Speed［J］.Technometrics，2009，51(2):162-172.

［3］MAHMOUD M S，MEMON A M，SHIPeng.Observer-Based Fault-Tolerant Control for a Class of Nonlinear Networked Control Systems［J］.International Journal of Control，2014，87(8):1707-1715.

［4］CORPORATION H P.Observer-Based Robust Control for Hydraulic Velocity Control System［J］.Mathematical Problems in Engineering，2013，29(1):61-61.

［5］CHEN MIN-SHIN，CHEN CHI-CHE.H∞Optimal Design of Robust Observer against Disturbances［J］.International Journal of Control，2014，87(6):1208-1215.

［6］WU Q H，JIANG L，WEN J Y.Decentralized Adaptive Control of Interconnected Non-Linear Systems Using High Gain Observer［J］.International Journal of Control，2004，77(8):21-30.

［7］KULKARNI A，KUMAR A.Dynamic Recurrent Wavelet Neural Network Observer Based Tracking Control for a Class of Uncertain Nonaffine Systems［J］.International Journal of Intelligent Systems and Applications，2012，4(11):53-61.

［8］SHARIATIO，MOHD ZIN OO，KHAIRUDDIN A.Developmentand Implementation of Neural Network Observers to Estimate Synchronous Generators'Dynamic Parameters Using On-Line Operating Data［J］. Electrical Engineering，2014，96(1):45-54.

［9］JIANG Zhaohui，TAIKI ISHITA.A Neural Network Controller for Trajectory Control of Industrial Robot Manipulators［J］. Journal of Computers，2008，3(8):1-8.

［10］ERKAYA S.Prediction of Vibration Characteristics ofa PlanarMechanism Having Imperfect Joints Using Neural Network［J］. Journal of Mechanical Science and Technology，2012，26(5):1419-1430.

［11］李秀改，黄德先.基于动态反馈神经网络的复杂系统预测控制［J］.吉林大学学报:信息科学版，2004，22(4):369-372. LIXiugai，HUANG Dexian.Model Predictive Control for Complex Systems Based on Dynamic Recurrent Neural Network［J］. Journal of Jilin University:Information Science Edition，2004，22(4):369-372.

［12］姜寅令，于显利.机器人多模型反演滑模控制策略研究［J］.吉林大学学报:信息科学版，2014，32(4):418-423. JIANG Yinling，YU Xianli.Multi-Model Back-Stepping Sliding Mode Control of Robotic Manipulators［J］.Journal of Jilin University:Information Science Edition，2014，32(4):418-423.

(责任编辑:何桂华)

Improved Neural Network State Observer Designed for Nonlinear System

JIANG Yinling，LIYanhui，WANG Haixing

(College of Electrical Information and Engineering，Northeast Petroleum University，Daqing 163318，China)

For reducing the dependence of nonlinear observer on the precision model，a non conventional NN (Neural Network)observer for nonlinear system is proposed.The neuro-observer is a three-layer feedforward neural network，which is trained extensively with the error backpropagation learning algorithm including a correction term to guarantee good tracking and bounded NN weights.Designing the neural network observer is using artificial neural network to identify the nonlinear parts of the system and using a Luenberger observer to reconstruct the states of the system.The Lyapunov directmethod is used in order to ensure the stability of the proposed non-conventional observer.The proposed observer is applied to 2 degrees of freedom horizontal manipulator to evaluate its performance.The simulation results show that the state observation of uncertain systems can be solved by themethod and it is suitable for the low precision model of the nonlinear system.

neural network observer;nonlinear system;manipulator

TH868

A

1671-5896(2015)04-0471-05

2015-02-05

黑龙江省科学基金资助项目(QC2013C066);黑龙江省普通高等学校青年学术骨干支持计划基金资助项目(1254G004)

姜寅令(1980— )，女，辽宁庄河人，东北石油大学讲师，博士研究生，主要从事滑模控制、机器人智能控制研究，(Tel) 86-13945602852(E-mail)jiangyinling@nepu.edu.cn;李艳辉(1970— )，女，黑龙江法库人，东北石油大学教授，博士生导师，主要从事鲁棒控制研究，(Tel)86-459-6504634(E-mail)ly_hui@hotmail.com。