基于DEA交叉效率模型的省际节能减排效率评价

段显明，胡玉筱

(杭州电子科技大学 管理学院，浙江 杭州310018)

交叉效率评价的目的是要对各个决策单元的效率值进行排序［1］，交叉效率值不是仅仅根据被评估决策单元自身的权重而得到，它是基于所有决策单元的权重而计算得到的，也即在决策单元自评估的基础上，加进了其余决策单元的交叉评价，这有利于各决策单元效率优劣性的排序［2］。然而，Despotis 认为，在使用交叉效率模型时，最优权重的确定却不一定是唯一的，这给最后的交叉效率值带来了一定的不确定性［3］。很多研究在计算交叉效率值的时候，所用的权重值为各决策单元权重的简单算术平均。Wu 等人将各决策单元当作合作博弈环境下的一个角色，根据决策单元的夏普利值得到的聚合权重被分别定义为博弈的关键解决方案［4］。最后，Wang ＆ Chin 提出了有序加权平均的权重处理方法，该方法可以在最后的整体效率评估中加入决策制定者的偏好［5］。也就是说，在交叉效率研究中，除了激进式评价和仁慈式评价外，还有很多其它方法的存在。

现有研究中专门针对节能减排效率问题进行探究的不是很多，而使用交叉效率研究的更少。节能减排是国家“十一五”规划纲要提出的政策目标，2010年是本轮规划的最后一年，因此本文选择本年度的节能减排数据进行探讨，评估各省市的节能减排效率。

一、模型与方法设计

(一)CCR 模型设计

设有n 个决策单元，每一个决策单元对应m 种输入和s 种输出，对于决策单元DMUj来讲，将其第i项输入记作xij，将其第r 项输出记作yrj。在标准交叉效率评估中，通常使用DEA 模型中的CCR 模型给出的权重计算交叉效率值。

对于决策单元DMUk而言，设其第i 项输入对应的权重为ωik，其第r 项输出对应的权重为λrk，则其总输出Ok与总输入Ik的比值Ekk为:

通过该式得到的有关DMUk的Ekk值即为该决策单元的效率评价指数，也即是该决策单元的效率值。为了得到该评价指数的值，可以通过DEA 的CCR 模型来实现。模型就将问题转化为求解以下极大化问题:

式(2)是一个分式规划问题，通过使用Charnes-Cooper 变换，可将该式化为下列等价的线性规划问题［6］:

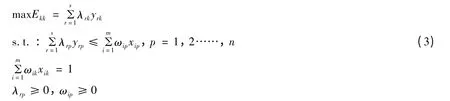
该模型约束下，Ekk是根据最有利于决策单元DMUk的权重计算得来的，因此，该模型所得的Ekk的大小也可以称作为DMUk的自我评价指数［7］。如果该指数Ekk的值为1，则认为DMUk是有效的;如果Ekk＜1，则认为DMUk是无效的。而在实际中，通常会出现有多个决策单元的效率值为1 的情况，而且这些效率值的得出都是通过使用最有利于自身的权重而得到的，这样就无法有效区分不同决策单元效率的优劣，所以，为了避免这种现象的发生，我们采用每一个最有利于决策单元自身的权重值去评价其余的决策单元，实现交叉效率的评价。

(二)交叉效率评价模型

由于自我评价模型(3)得出的权重值不唯一，这会导致最终得到的交叉效率评价指数具有不确定性，为了避免这种不确定性情况的出现，我们这里采用对抗型交叉效率评价。对抗型交叉效率评价的思想是，每一个决策单元在首先保证自身效率值尽可能大的同时，尽量压低其它决策单元的效率值。具体实现步骤如下:

step 1:利用模型(3)计算出DMUk的自我评价值Ekk;

step 2:求解以下线性规划问题:

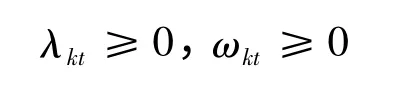
其中k=1，2，……，n;t=1，2，……，n

step 4:将step(3)中得到的交叉效率评价值组成交叉评价矩阵E

其中，主对角线元素Ekk为自我评价值，非主对角线元素Ekt(k≠t)为交叉效率评价值。

二、实证分析

(一)节能减排指标的选取

本文选择全国30 各省(除西藏、港澳台外)为研究对象，研究其在2010年实施节能减排政策的实施效率。在投入和产出指标的选取方面，现有研究通常将能源、水消耗量和环境容量资源的使用选作投入指标，而将产出指标界定为反映经济发展程度和节能减排成果的参数［8－10］。通过借鉴现有研究的成果，这里将环境资源消耗作为投入指标，具体从能源消费总量(以标准煤计算)、供水总量、工业废水排放量和工业二氧化硫排放量四个指标来考虑;产出指标显示经济是否发展、减排效果如何，这里从地区生产总值、工业废水排放达标量和工业二氧化硫削减量三个方面来考虑。本文所选的2010年中国30个省市的节能减排投入和产出数据来自《2011 中国统计年鉴》、《2011 中国环境统计年鉴》。

(二)模型分析结果

将选取的投入产出数据输入到软件，而由软件执行得到的最终结果为基于交叉效率模型的交叉效率值矩阵E，Eij为省份i 对省份j 的交叉评价结果(i，j∈［1，30］)，其中i 或j=1 ～30 分别代表北京，天津……，新疆(具体顺序如表1 中所示)，限于文章篇幅，这里就不具体展开详述了。通过对交叉效率值矩阵E 进行观察可以看出，各决策单元对节能减排效率值的自我评价都较高，而对其它决策单元的评价都偏低，其中各决策单元的自我评价结果Eii如表1所示。软件执行的结果表明，除了青海、宁夏和新疆三个地区对自身的节能减排效率评价较低外，其余各地区对自身节能减排效率的评价值都在0.90 以上，这也显示了青海、宁夏和新疆三个省的节能减排效率的确偏低的事实。另外，所选取的30 个省份(西藏、香港、澳门和台湾数据缺失，未考虑在内)节能减排交叉评价效率值及其排序结果均在表1 中一一列出。

从以上的结果可以看出，DEA-CCR 模型下求得的各省市节能减排效率中有多个值为1 的情况存在，所以自我评价效率值Eii还不能有效地用于评估各地区节能减排效率的优劣，为此我们引入了交叉效率评价机制，该机制下得到的各决策单元节能减排效率值普遍较低，比较符合实际情况。从图可以看出，传统模型下得到的华北、东北各地区节能减排效率值大多虚高，主要是因为这些地区本身效率值较低，通过选择更有利于自身的权重计算得到了与实际有一定偏差的结果，这些地区仍然保有一定的传统高污染、高排放型企业，比如此时的首钢等高污染企业大大拉低了北京地区节能减排效率水平。通过对两种模型下得到的结果进行分析发现，除了自我评价模型下出现了多个效率值为1 的情况外，两种模型下的效率值排序基本一致，但交叉效率评价模型下的各效率值排序更为清晰，浙江、江苏等华东省份的节能减排效率最优，贵州、宁夏、内蒙古、青海、新疆以及东北三省等的效率最差，具体排序如表1所示。

从所得到的结果可以看出，各地区节能减排效率值和该地区的地域分布无显著性关联关系，和地区经济的发达程度也无显著相关关系。浙江、江苏、山东等省市的地区GDP 在全国领先，同时其节能减排效率也最高，说明这些省市在经济发展的同时，也开始将更多的精力投入到节能减排方面，正在走产业转型升级或资源节约化路线;而地区GDP 排名靠前的广东、上海和北京在交叉效率排名中分别排在了17、18 和20 名，说明这些省市在发展经济的同时，对节能减排的关注度较小，因此在节能减排效率的提升上面还有较大的空间。

表1 中国各省市节能减排效率的自我效率和交叉效率评价结果对比

(三)区域节能减排效率差异分析

按照国家统计局划分方法，我国31 个省、市、自治区(港澳台除外)按地理位置可以分为东中西三大经济区域，其中东部包括北京、天津、辽宁、河北、山东、上海、江苏、浙江、福建、广东、海南等;中部包括黑龙江、吉林、山西、安徽、江西、河南、湖北、湖南、内蒙古等;西部包括新疆、青海、甘肃、宁夏、陕西、西藏、四川、重庆、贵州、云南和广西等。东部经济区域交叉效率的平均值为0.721，中部经济区域的平均值为0.675，西部经济区域的平均交叉效率值为0.612，如此看来，我国各省市的节能减排效果整体呈现东、中、西依次降低的趋势。具体分析可以看出，浙江、江苏、山东、福建等东部靠南地区的节能减排效率要比辽宁、河北、北京等东部靠北地区更高，这主要是因为东部靠南地区资源相对匮乏，但其利用强大的经济优势，通过先进的技术应用和节能减排管理手段，大大提升能源的使用效率。中西部经济区域的节能减排效率相对较低，一方面是由于其本身自然资源相对比较丰富，容易走向高投入——低产出(低效率)式的粗放型发展道路;另一方面是由于其自身的产业结构相对不合理，经济实力相对较低，在能源使用技术方面的投入相对较少，故而中西部地区在节能减排效率方面还有较大的提升空间。

三、结束语

传统的DEA 方法能够清晰地分辨出决策单元的有效性与否，但是它也存在着一些缺陷，即不能够将决策单元的有效程度进行排序。基于这一不足，本文提出交叉效率评价的模型进行探究，从模型的分析结果可以看出，该模型在评价决策单元节能减排效率的优劣程度方面更为可靠。另外，节能减排是国家的重要发展战略，一些经济发达省市，如北京、上海和广东等地区，应该在保证地区GDP 增长的同时，向节能减排领域适当增加资本、人力和其它资源的投入，进一步加强节能减排效率的改进;青海、宁夏、新疆以及东北三省等正面临较为巨大的经济发展压力，但经济发展决不能走以牺牲环境为代价的粗放式增长道路，应该尽快引进东部经济区域的节能减排技术和管理手段，调整产业结构、提高能源效率。

［1］Charnes A，Cooper W W．Programming with linear fractional functionals［J］．Naval Research Logistics Quarterly，1962(9):181－186．

［2］Ruiz Jose L，Sirvent Inmaculada．On the DEA total weight flexibility and the aggregation in cross-efficiency evaluations［J］．European Journal of Operational Research，2012，223(3):732－738．

［3］Despotis D K．Improving the discriminating power of DEA:focus on globally efficient units［J］．Journal of the Operational Research Society，2002，53(3):314－323．

［4］Jie Wu，Liang Liang，Feng Yang．Determination of the weights for the ultimate cross-efficiency using Shapley value in cooperative game［J］．Expert Systems with Application，2009，36(1):872－876．

［5］Ying-Ming Wang，Kwai-Sang Chin．The use of OWA operator weights for cross-efficiency aggregation［J］．Omega，2011，39(5):493－503．

［6］盛昭瀚．DEA 理论、方法与应用［M］．北京:科学出版社，1996．

［7］许波，刘征．Matlab 工程数学应用［M］．北京:清华大学出版社，2000．

［8］于鹏飞，李悦，郗敏，等．基于DEA 模型的国内各地区节能减排效率研究［J］．环境科学与管理，2010，35(4):13－16，20．

［9］陈清霞．长三角节能减排效率评价研究［D］．上海:上海交通大学，2010．

［10］郭彬，逯雨波．我国中部六省节能减排效率测评及其影响因素分析［J］．技术经济，2012，31(12):58－62．