基于神经网络的液压滚切剪剪切力预报模型

2015-11-28吴会敏朱清智

精密制造与自动化 2015年4期

吴会敏朱清智

基于神经网络的液压滚切剪剪切力预报模型

吴会敏朱清智

（河南工业职业技术学院河南南阳473000）

通过分析滚切剪的工作过程，选择数学模型与神经网络型相结合的乘法网络，设计了基于BP神经网络的液压滚切剪剪切力预报模型。通过对切入阶段和滚切阶段剪切力的数学模型计算值、实测值和预报值的比较，证明了由该剪切力预报模型计算的剪切力精度有了很大提高。

BP神经网络液压滚切剪剪切力预报模型

传统的液压剪切机是中厚板生产线上的重要设备，完成对轧件的切头、切尾、切定尺、取样[1]。生产线上大多数采用斜刃剪，其上剪刃是倾斜的，有利于减小剪切力，但是剪后的钢板有横向弯曲、断面塌角等缺陷[2]。滚切剪有效地解决踏角和“啃伤”缺陷问题，而且剪切断面好，是中厚板生产线不可缺少的剪切设备[3]。

随着对钢板质量要求的提高，钢板种类日益增多。当滚切剪需要剪切一个新的钢种时，滚切剪机需要承受多大的剪切力、是否超出了设备的加工能力，目前都是根据以往经验预估计剪切力的大小，这种方式可靠性很低，容易造成设备的损坏和财产损失[4]。本文以某钢铁公司2 800 mm生产线定尺滚切剪的改造项目为依托，采用BP神经网络与数学模型相结合，设计了全液压滚切剪剪切力预报模型，仿真结果表明可以有效提高剪切力的计算精度。

1 液压滚切剪最大剪切力公式的推导

滚切剪为上切式，由液压站带动左右两个和机架铰接的卧式液压缸，推动左右两个连杆，两个液压缸按照设定的位置与速度曲线移动，带动上刀架实现纯滚动剪切运动[5]。剪切过程主要有三个阶段：切入阶段、滚切阶段、切离阶段。滚切剪最重要的剪切过程是切入和滚切阶段。在切入阶段钢板经历弹性压入到塑性滑移的过程，在滚切阶段经历弹塑性压入到裂纹扩展的过程[6]，这两个过程截然不同。滚切剪切入阶段最大剪切力公式为：

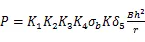
滚切剪滚切阶段最大剪切力公式为：

2 基于BP神经网络的剪切力预报模型的设计

2.1 基于BP神经网络的剪切力预报模型工作原理

液压滚切剪剪切力修正模型原理图，如图1所示。剪切吨位由用户输入，钢板的材料性能在板材库中查询得到，钢板的厚度、宽度由通信模块得到，作为BP网络输入值；BP网络经过前向计算得出网络的输出值送到数学模型中，计算后得到预报剪切力，根据实测剪切力与预报剪切力的差值采用反向传播算法来修正权值，直到预报值达到精度要求，然后将最终的预报值存入到经验知识库中。

图1 液压滚切剪剪切力预报模型原理图

2.2 基于BP神经网络的剪切力预报模型的结构设计

1）输入输出层的确定

2）网络结构确定

网络的训练样本主要来自生产线上的实测数据和专家提供的经验数据。在训练本网络时，共选择样本值500组，其中450组参加训练作为训练样本，50组不参加训练作为网络的检测样本。

借助Matlab平台构建神经网络，对具有不同隐含层结构的BP网络进行训练。通过比较网络的全局误差来判断最佳的隐含层结构。

本文对不同隐含层结构的网络都训练了10次，取误差最小的一次作为实验结果。实验结果如表1所示，由表可知：具有三个隐层的神经网络具有最好的收敛性；隐层节点数为8个时，神经网络的收敛性最好。所以，确定剪切力预报模型的神经网络结构具有三个隐层，每个隐层节点数是8个。

表1 不同隐含层结构BP网络训练的全局误差

剪切力预报模型的神经网络结构，如图2所示。

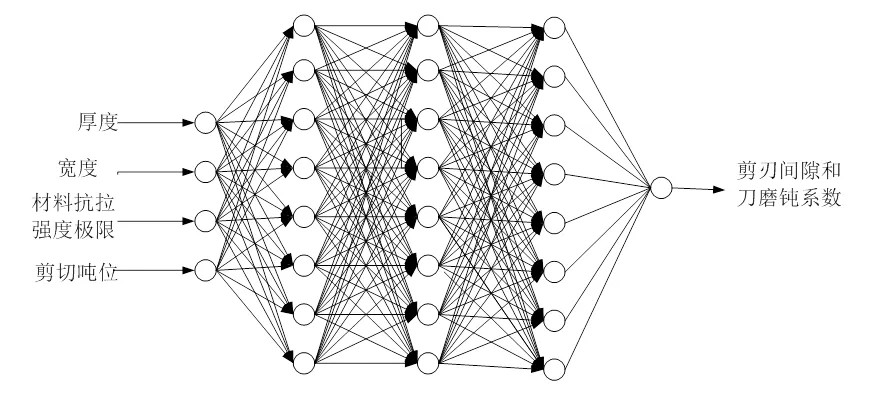
图2 剪切力预报模型的神经网络结构

3 BP神经网络在MATLAB中的实现

MATLAB环境下，五层BP神经网络实现程序如下：

A=load(‘D:PmgramFilesMATLABworkin.txt’)；

A=A’；%输入样本

B=load(‘D:Pmgram FilesMATLABworkout.txt’)；

B=B’；%输出样本

Para.Goal=0.0001；%网络训练目标误差

Para.Epochs=1000；%网络训练代数

Para.LearnRate=0.1；%网络学习速率

Para.Show=10；%网络训练显示间隔

Para.LearnFcn=‘learngdm’；%网络学习函数

Para.PerformFcn=‘mse’；%网络的误差函数

Para.InNum=size（Input，1）；%输出量维数

Net=newff（minmax（A），[8 8 8 1]，{‘tansig’，‘tansig’，‘tansig’，‘purelin’}，‘trainlm’）； %创建一个5层BP神经网络，隐含层节点数分别为8,8,8，输出层节点数为1

Net.train Param.show= Para.Show；%训练显示间隔赋值

Net.train Param.goal= Para.Goal；%训练目标误差赋值

Net.train Param.lr= Para.LearnRate；%网络学习速率赋值

Net.train Param.epochs= Para.Epochs；%网络训练代数赋值

夜里她一直在书房看稿子。厚厚一摞打印稿，她需要在睡觉以前看完。天气闷热，大雨倾盆，念蓉起身，去阳台关好窗子。楚墨还没有回来，两个小时以前她给楚墨打电话，楚墨说他正在与朋友吃饭。电话里声音嘈杂，隔着电话念蓉也能闻到浓重的酒精气味。念蓉问他：“要不要我过去帮你把车开回来？”楚墨大着舌头说：“我不开车，我飞回去。”

[Net，tr]=train（net，A，B）；%训练网络

T=load（D:Pmgram FilesMATLABwork est-in.txt’)；

%样本测试

T=T’； %测试样本输入

M=load(‘D:Pmgram FilesMATLABwork est-out.txt’);

M=M’； %测试样本输出

y=sim（Net，T）；％计算训练样本输出值。

采用500组训练样本，剪切力模型BP网络在235次训练后收敛，其网络训练误差曲线图如图3所示。

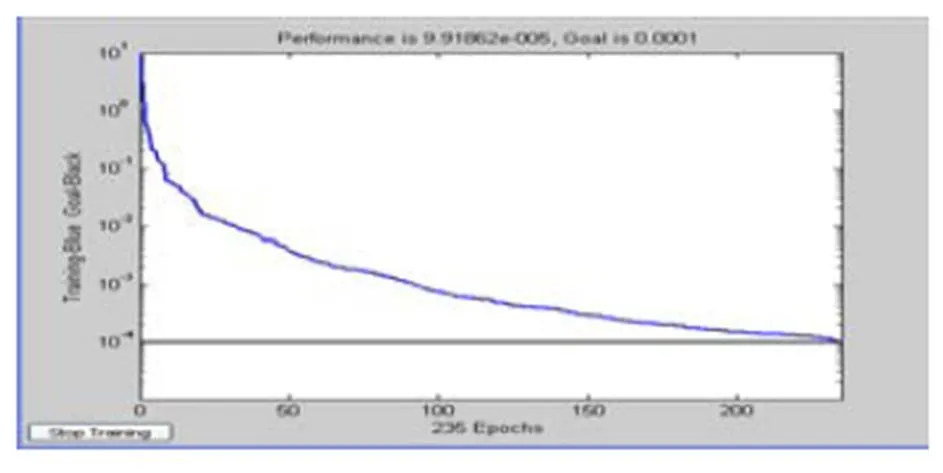
图3 剪切力预报模型BP网络误差曲线

4 液压滚切剪剪切力预报模型的实现

在Labview编程环境中，滚切剪剪切力预报模型操作界面如图4所示。

图4 液压滚切剪最大剪切力预报模块操作界面

利用网络修正后的剪刃间隙和刀磨钝系数预报切入阶段和滚切阶段剪切力，然后用数学模型计算剪切力，两者分别于实测值进行对比，用曲线图显示，横坐标表示样本点序号，纵坐标表示样本误差值。切入阶段和滚切阶段剪切力预报模型误差曲线分别如图5和图6所示。

图5 切入阶段剪切力误差曲线图

图6 滚切阶段剪切力误差曲线图

分析图5和图6可得出以下结论：切入阶段剪切力公式计算值与实测值相比误差在10.2%～16.7%之间，网络模型预报值与实测值的误差在3.6%～6%之间；滚切阶段剪切力公式计算值与实测值相比误差在9.3%～16.8%之间，网络模型预报值与实测值的误差在3.8%～6.4%之间。预报误差远远小于计算误差，将BP神经网络运用到滚切剪的剪切力预报模型，确实可以大大减小计算误差，通过剪切力预报模型计算出的剪切力可以作为评量滚切剪工作能力的可靠依据。