基于振动信号的齿轮可靠性评估

段慧云，王细洋

(南昌航空大学 航空制造工程学院，南昌 330063)

0 引言

可靠性是指产品、系统在规定的条件下，规定的时间内，完成规定功能的能力［1］。它是评价设备质量的重要指标之一。随着现代机械设备制造日趋向自动化、精密化和高效化发展以及提倡的可持续发展战略，可靠性也逐渐被人们所重视，它成为机械产品质量的重要衡量标准。设备的运行状态信息能够有效地反映出设备的运行动态特性、工作精度和性能退化规律，为设备运行的可靠性评估提供重要信息［2］。本研究提出一种基于设备振动信号的运行可靠性评估方法，该方法基于比例故障率模型建立了设备振动信号与可靠性指标之间的映射关系，从而实现设备的可靠性评估。将其应用于齿轮可靠性评估，利用齿轮箱的实时监测数据实现设备运行可靠性评估，为机械设备的运行可靠性评估提供了新的理论技术和定量性的参考依据。

1 基于威布尔比例故障率模型的可靠性评估

在比例故障率模型中，不同个体的失效率函数之间均成比例，其优点在于将反映设备运行状态的特征指标与设备的故障率之间建立联系［3］。该方法在考虑瞬态失效的硬故障的同时又可兼顾性能退化的软故障，将反映设备运行状态的信号特征指标与可靠性指标(如可靠度等)之间建立联系，从而实现运行可靠性的评估。可靠性评估能够对设备运行状态信息进行实时监测及分析，因此为基于状态信息的故障预防及维修提供了帮助。

机械设备在运行过程中一般随着时间的增长性能逐渐衰退，失效程度也随之递增。失效模式常用的参数模型有很多，比如威布尔分布、正态分布、指数分布和对数正态分布等，其中，威布尔分布是近年来在可靠性分析领域使用最普遍的分布之一，它的失效率函数根据不同的特性可分为3类，即随着时间递减的、维持恒定的和随着时间呈现递增的。浴盆曲线如图1 所示，可根据图中显示的曲线形状分为对应的3 个阶段:早期失效期、随机失效期和损耗失效期［4-6］。威布尔分布具有参数的多元化以及富有弹性的特点，已被广泛应用在现代工程对设备失效建模以及可靠性评估中。

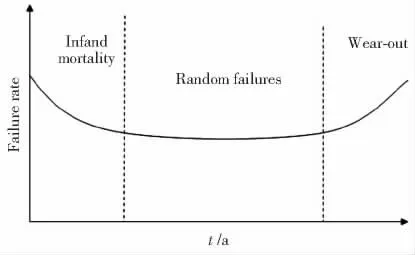
图1 浴盆曲线Fig.1 Bathtub curve

1.1 威布尔分布模型

威布尔分布作为使用最普遍的可靠性模型之一，在很多领域内都获得了显著的研究成果和发展。Arjun K.Gupta 等［7］提出二维Weibull-Geometric 分布模型并将其应用于实例;代卫卫等［8］通过对DBT3 ×1000 型刮板输送机的运行故障进行统计分析，构建了威布尔分布模型并获取其寿命分布模型，以此分析该机型的故障规律，对分布模型进行优选后即可实现设备的可靠性指标的计算以及寿命的预测;丁锋等［9］将模型应用于铁路机车轮对轴承的可靠性评估中，也验证了该方法的有效性和合理性。

威布尔分布的故障密度函数为

失效分布函数为

可靠度函数为

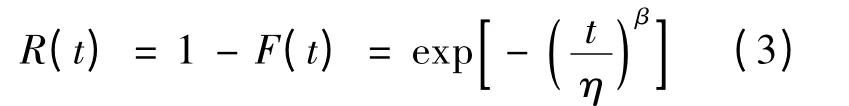
故障率函数为

式中:β 为威布尔分布的形状参数，η 为威布尔分布的尺度参数。

1.2 威布尔比例故障率模型

将威布尔分布作为基准分布，构建比例故障率模型，即转换为威布尔比例故障率模型。

式中:Z 表示响应协变量，优选对设备状态敏感的特征参量;γ 为协变量Z 对设备故障率的影响，称为回归参数。

式(5)中，γZ 是协变量的线性组合，可以看出比例故障率模型的状态协变量与失效率函数具有乘法效应。比例故障率模型综合考虑了设备在不同情况下的运行状态特性，实现从运行状态特征到可靠性指标的映射关系，为设备的可靠性评估以及预防维修提供重要帮助。

至时间t 时，基于状态信息的状态退化特征的威布尔比例可靠度函数R(t;Z)可以表示为

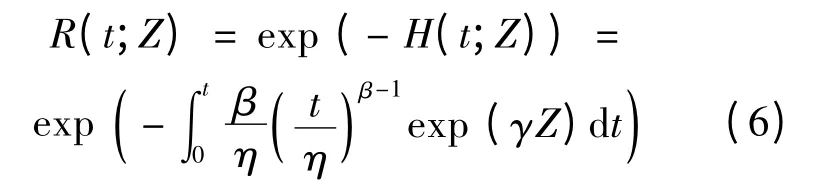
2 极大似然参数估计

为了实现比例故障率模型的可靠性评估，首先需要对其进行模型参数的估计。关于威布尔分布的参数估计，虽然至今已有了大量的研究成果，但仍较难得到应用在工程实际中。如:徐微等［10］构建了两参数威布尔分布的设备可靠性寿命分布模型，通过最小二乘法关于水平残差和垂直残差平方和最小两种方法来对其进行参数估计并进行比较，但是最小二乘法的估计通常依赖于经验信号分布函数;方华元等［11］对遗传算法进行了优化，这种算法虽然在一定程度上提高了可靠性评估的精度，但是由于这种算法的随机性，导致其结果不可避免的波动性。而极大似然估计是一种十分有效和通用的参数估计方法，在参数估计问题中占有重要地位，尤其在处理不完全寿命的情况下，极大似然估计具有明显的优势。

通过给定设备的运行状态，对全寿命周期振动信号进行采集，以此来获取比例故障率模型中的各个参数。基于振动信号提取能够反映设备运行特性的特征参数，如寿命时间、截尾时间以及失效的特征数据个数等，将数据按采样时间列为(t1，t2，…，ti)，将参数列为θ(β，η，γ)，将可靠度函数和故障概率密度函数代入似然函数中，即可得到似然函数

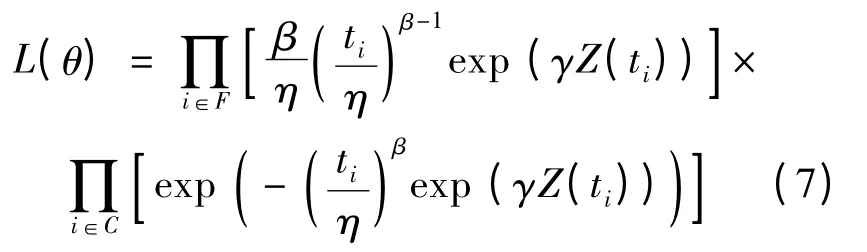
式中，F 为失效集，C 为截尾集。

对式(7)两边同时取对数，得

根据极大似然评估方法，采用Nelder-Mead's迭代优化算法［12］，设定优化估计的初始值，通过利用Matlab 优化工具箱对函数进行优化，即可求解获得β、η 和γ。

在得到比例故障率模型的各参数后，就可以将故障率表达为能够有效反映其工作状态特性的特征参量Z 和设备工作时间t 的函数表达式，从而获取可靠度以及故障率等指标。基于比例故障率模型的可靠性评估流程图如图2 所示。

图2 基于比例故障率模型的可靠性评估流程图Fig.2 Flow chart based on the reliability evaluation of the proportion failure rate model

3 实例应用

3.1 齿轮振动信号采集

为了对齿轮振动信号进行采集分析，搭建试验台如图3 所示。图中分别是试验台外观图和数据采集硬件实物图。试验台的工作原理大致是:齿轮箱通过电动机进行驱动;将光电编码器用来连接电动机与齿轮箱，作为外部触发源获取同步脉冲信号，控制采集卡进行A/D 转换，实现齿轮箱转速的测量与信号采集;采用加速度振动传感器以磁吸的形式分别安装在箱体和基座上，它的工作原理是根据压电效应而对信号进行转换，可以通过调整加速度传感器的位置来采集不同部位的齿轮振动信号;试验台各设备之间用联轴器联结，并固定在基座上。传感器的采集信息通过恒流源放大器进行10 倍放大，然后连接到USB 模块数据采集卡将数据读入计算机，从而实现信号的采集与储存。

图3 齿轮箱振动信号采集试验台Fig.3 Test bench for gearbox vibration signal acquisition

利用试验台对齿轮箱进行全寿命周期实验，采用输入功率为4.5 kW，转速为1 750 r/min 的电动机对齿轮箱进行驱动。首先让齿轮箱在100%负载下连续工作96 h，然后将负载提升至额定的300%，在齿轮箱工作10.46 h 后，齿轮从正常运行状态至完全失效，有2 个轮齿完全断裂。试验中将采样频率设置为20 kHz，在试验初期，采样周期为60 min，采样时间为10 s，到试验中期，采样时间保持不变，此时适当调整采集时间间隔，采样周期缩短为30 min，到后期再逐渐缩小采样间隔。将采集的信号通过编码器经A/D 转换后按二进制文件格式将数据文件以采样时刻为分类存储在硬盘里。整个周期共采集了154 个数据文件，每个文件含200 k 个采样点。

3.2 响应协变量的选择

对齿轮箱进行性能退化分析的重点在于性能退化指标参量的获取，性能的退化指标参量是指设备本身的性能状态参数或者规定输出参数的变化程度。每一性能退化的敏感特征［13］，本研究采用小波包分析技术以精准的获取距离评估指数作为特征指标，克服以往响应协变量选择的盲目个特征指标参量不仅要兼备敏感性、稳定性和代表性，同时还要物理意义明确，且便于监测。当齿轮箱状态发生变化时，性能特征参量要能够在尽可能排除外界干扰的情况下有效地反映出其运行状况的真实状态。因此，性能退化指标参量和失效标准的确定对于设备的性能退化分析来说起着极为重要的作用。距离评估技术能更全面的表现出设备和局部性。

将采集到的齿轮全寿命周期振动信号基于Matlab 软件通过时域同步平均技术对其进行去噪等预处理后，再进行第二代小波包分解。针对振动信号的特性，基于Daubechies 小波基不仅具有N 阶消失矩，又具有紧支性和近似对称性的特点，优选出该系列的小波基实现能够表征齿轮箱性能退化的敏感响应特征指标的提取。通过比较最终优选出N=10，即db10 小波基对齿轮振动信号进行分析。通过对齿轮初始振动信号进行频谱分析，观察其采样频率及信号能量的频带分布状况，选用3 层分解，则经分解得到的各频带能量可表示为

基于小波包分析技术以及频带能量，分别计算出K 中第i 个特征指标的距离评估指数αi。αi越大对故障的敏感性就越强，对故障进行分类的效果就越好。获取的距离评估指数如图3 所示，选取αi中较大的2 个特征指标应用于响应协变量中，即图中的P3，3和P3，5所对应的点。

3.3 基于振动信号的齿轮可靠性评估

采用能够反映设备运行状态的距离评估因子α1和α2作为响应协变量，将其代入故障率函数中，则威布尔比例故障率模型即可表达为

式中，Z1为距离评估指数α1，Z2为距离评估指数α2。

采用极大似然估计方法对威布尔比例故障率模型进行参数估计，通过对齿轮全寿命周期的运行状态设定优化函数的搜索初始值，最后可以得到最优化参数的估计结果(图4)，分别对应了β、η、γ1和γ2的值。

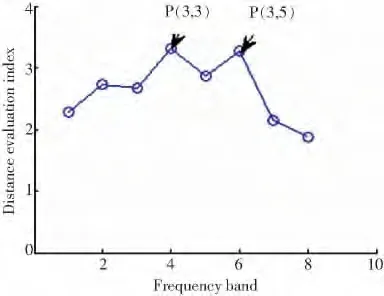
图4 距离评估指数Fig.4 Distance evaluation index

表1 各参数估计结果Table 1 Parameter estimation results

根据参数估计可以得到齿轮的比例故障率函数，从而得出齿轮全寿命周期的可靠性指标，图5是基于模型的可靠性评估曲线，反映了齿轮在全寿命周期过程中不同运行时刻对应的可靠度的大小及整体发展趋势。

从图4 中可以看出，齿轮的全寿命周期可以大致分为3 个状态阶段:正常工作状态、性能退化状态以及准失效状态。正常状态可以认为是磨合状态和稳定磨损期前期，性能退化状态可以认为是稳定磨损期后期与加速磨损期，准失效状态为磨损较严重，应该停机检查，作出相应的处理措施。

齿轮的性能退化过程主要发生在负载提高至300%之后，从齿轮全寿命周期的时域特征指标可以观察到，像峰值、均方值等有量纲参数在123 号文件后波形发生突变，这是因为有量纲参数对载荷的变化较为敏感。在124～140 号文件过程中波形又相对稳定，这时处于齿轮的性能高速退化阶段。140 号文件之后波形又发生突变，这时即齿轮的失效状态阶段。将齿轮箱实际的性能退化状态结合可靠度曲线图，对由运行可靠度决定的齿轮运行状态进行分类，如表2 所示。

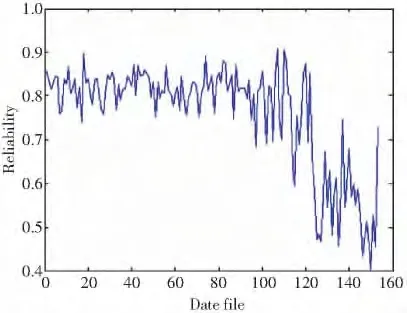
图5 全寿命周期运行可靠度曲线图Fig.5 Whole life cycle operation reliability graph

表2 可靠度对应运行状态分类Table 2 Classification of reliability running state

若运行可靠度大于0.65，表明设备处于正常工作状态;若运行可靠度低于0.65 而高于0.47，说明设备处于性能退化阶段，此时应及时对齿轮箱进行检查和维修;若运行可靠度低于0.47，说明齿轮箱已处于准失效状态，应及时停机维护。

为了检验所采用的可靠性评估的准确性，对同型号的齿轮箱进行振动信号采集。首先让齿轮箱在100%负载条件下，连续工作256 h;然后将负载提升至额定的200%，在齿轮箱工作47.5 h后，齿轮从正常运行状态至完全失效，有4 个轮齿完全断裂以及2 个轮齿部分破损。试验中设置同样的采样频率20 kHz 和采样时间10 s，采样周期由初期的60 min 至实验中期缩短为30 min，并在后期逐渐缩短采样间隔，共采集320 个文件。对文件数据进行可靠度计算以及状态识别，任选出20 组分别在不同运行状态下的采集信号来进行齿轮可靠性分析验证，分析结果如图6 所示。在选取的总共60 个数据文件的可靠度分析中，有效识别数有52 个，识别率达86.67%，可以看出，通过可靠度阈值来评估齿轮运行状态是可行的。

图6 齿轮可靠度评估验证Fig.6 Gearbox reliability analysis comparison results

4 结论

1)以齿轮箱的齿轮啮合振动信号作为研究对象，结合威布尔比例故障率模型，提取距离评估指数作为特征指标，并采用极大似然估计等算法，从而获取比例故障率函数，实现齿轮的可靠性评估。

2)试验结果表明:通过小波包分析和距离评估技术可以快速准确地提取距离评估指数;将距离评估指数作为特征指标对于故障分类效果好;基于模型对齿轮啮合振动信号进行可靠性评估的方法对齿轮性能退化状态识别率达86.67%，识别效果较理想。

［1］董健，胡海波，陈桂明，等.面向任务需求的武器装备作战适用性评价指标体系研究［J］.价值工程，2013(26):312-313.

［2］蔡改改，陈雪峰，陈保家，等.利用设备响应状态信息的运行可靠性评估［J］.西安交通大学学报，2012，46(1):108-113.

［3］丁锋.基于主动监测机制的装备可靠性评价新思路［J］.制造业自动化，2009，31(9):44-45.

［4］于晓红，张来斌，王朝辉.基于新的威布尔分布参数估计法的设备寿命可靠性分析［J］.机械强度，2007，29(6):932-936.

［5］何正嘉，曹宏瑞，訾艳阳，等.机械设备运行可靠性评估的发展与思考［J］.机械工程学报，2014，50(2):171-186.

［6］孙闯，何正嘉，张周锁，等.基于状态信息的航空发动机运行可靠性评估［J］.机械工程学报，2013，49(6):30-37.

［7］Gupta A K，Kundu D.On bivariate Weibull-Geometric distribution［J］.Journal of Multivariate Analysis，2014，123(1):19-29.

［8］代卫卫，刘混举.基于威布尔分布的刮板输送机可靠性寿命分析［J］.机械工程与自动化，2013(1):139-141.

［9］丁锋，何正嘉，訾艳阳，等.基于设备状态振动特征的比例故障率模型可靠性评估［J］.机械工程学报，2009，45(12):89-94.

［10］徐微，胡伟明，孙鹏.基于两参数威布尔分布的设备可靠性预测研究［J］.中国工程机械学报，2013，11(2):112-116.

［11］方华元，胡昌华，樊红东，等.基于GA 的可靠性寿命分布参数的极大似然优化估计［J］.上海航天，2006(2):50-53.

［12］Lagarisa J C，Reeds J A，Wright M H，et al.Convergence properties of the Nelder-Mead simplex method in low dimensions［J］.SIAM Journal of Optimization，1998，9(1):112-147.

［13］卢娜，肖志怀，张广涛，等.基于自适应多小波与综合距离评估指数的旋转机械故障特征提取［J］.振动与冲击，2014，33(12):193-199.