基于小波包和EMD 的谱峭度法在滚动轴承故障诊断中的应用

张 斌，王细洋

(南昌航空大学 航空制造工程学院，南昌 330063)

0 引言

滚动轴承是各种旋转机械中应用最广泛的机械零件，经常工作在高速、重载等恶劣的环境中，是旋转机械中最易损坏的零部件之一。它的工作状态好坏直接影响整台机器的性能［1-2］，因此有必要对滚动轴承的状态监测和故障诊断做深入的研究。

共振解调法［3］是目前工程实际中最常用的滚动轴承故障诊断方法之一，它的原理依据是在滚动轴承振动信号中，故障会对轴承的高频共振成分产生调制现象，因此需要用带通滤波器提取高频共振成分，然后经Hilbert 变换做包络解调从高频共振成分中分离出故障信号，观察包络谱图中是否出现突出的故障特征频率的谱线，以此来诊断轴承是否发生故障。但是共振解调法有个很关键的前提——如何选择带通滤波器参数。近年来许多学者针对滚动轴承故障诊断理论及应用做了大量的研究。Huang［4］、杨宇［5］等发现使用EMD 分解信号时，可以直接从信号自身产生不同的基函数，因此EMD 作为一种自适应性的分解，能够生成有限个包含不同时间特征尺度的IMF分量，据此可以有效地排除干扰，只研究感兴趣的IMF 分量。朱汉明［6］将共振解调技术与Hilbert-Huang 变换相结合，利用了EMD 分解的自适应性减少了无关噪声的影响，提高了信噪比，但是如何确定带通滤波器却没有提出。何岭松等［7］发现在整个频带范围内，应用连续复Morlet 小波变换对信号进行包络分析时能够自动确定滤波器中心频率，但由于相对固定的复Morlet 小波波形参数，使得小波与故障成分的匹配性不好，影响了包络效果。胡晓依等［8］发现将STFT 应用于滚动轴承故障诊断中时，通过对滚动轴承振动信号做解调分析，在不同频段内计算解调信号的峭度值，可以确定最佳滤波频带，但是较大的计算量局限了该法的应用。Dwyer［9］认为将信号通过理想滤波器组后，计算输出信号每根谱线的峭度值即为谱峭度(Spectral Kurtosis，SK)。Antoni［10-12］给出了谱峭度的正式定义和快速谱峭度图的算法，并将谱峭度应用于机械故障的诊断中，取得了一定的成果。石林锁［13］在滚动轴承的故障诊断中应用一种基于连续小波变换和谱峭度的改进包络分析方法，具有一定的效果，但没有解决如何确定带通滤波器的参数。

此外，应用传统方法设计带通滤波器所要考虑的因素，比如滤波器的类型、滤波器阶数、滤波器的通带起伏、阻带衰减、过渡带宽的确定等，会对滤波的效果产生很大的影响，往往所处理的信号是非平稳的信号，对非平稳信号使用传统滤波器滤波的结果并不理想。而将小波包［14-16］作为滤波器使用会获得比传统滤波器更好的效果。

基于此，本研究提出一种基于谱峭度法和经验模式分解(EMD)，以及小波包变换联合应用的滚动轴承故障诊断方法，首先采用EMD 对原始信号进行自适应性分解，突出高频共振成分，再利用谱峭度确定合适的滤波器参数，然后使用小波包变换对高频共振信号进行带通滤波，最后使用包络解调进行故障诊断，并通过实际故障信号进行验证。

1 滚动轴承故障诊断流程

谱峭度法诊断机械故障虽然具有一定的效果，但是最能发挥其长处的则是利用其细查整个频域，寻找故障信息最为明显(峭度最大)的那些频带，并自动地在快速谱峭度图上显示出峭度最大处对应的中心频率和带宽，据此确定最佳带通滤波器参数。

EMD 作为一种自适应性的分解，生成有限个包含不同时间特征尺度的IMF 分量，可以用它减少低频干扰，突出高频共振成分，并提高原始信号的峭度。但有两点需要注意的是:

1)在EMD 分解中，由于边界效应、过包络和欠包络等原因，常常会出现与原始信号无关的伪分量，这些伪分量所含的频率成分通常与期望的特征频带重合，会对信号分析的结果产生干扰，要想得到较为精确的分析结果就必须排除伪分量的干扰。文献［17］提出的方法适用于伪分量的鉴别，即通过计算IMF 与原始信号之间的互相关系数，其中真分量与原始信号的互相关系数较大，而伪分量与原始信号的互相关系数较小。因此，通过定量地分析各IMF 与原始信号的相关性，就可以判定IMF 的真伪。

2)峭度是一个无量纲参数，可用于描述信号概率密度函数尖峰度。峭度值K 的定义为:

式中，μ、σ 分别为信号x 的均值和标准差，E(t)表示变量t 的期望值。峭度对信号中的冲击成分非常敏感。从工程实际经验来讲，无故障轴承振动信号的峭度值上限为3，当某些IMF 的峭度值大于3 时，说明这些IMF 中含有较多的冲击成分，重构这些IMF，得到的合成信号与原始信号相比，其峭度值会有显著的提高。

在实际的诊断过程中，需要综合考虑以上两点，确定到底重构哪些IMF，从而达到减少低频干扰，突出高频共振成分，并提高原始信号峭度的目的。

小波包是一种具有多分辨率的时频分析工具，特别适用于对非平稳信号的分析，它不仅能够描述信号的低频近似成分，更能刻画信号的高频细节成分，将其作为带通滤波器使用会取得比传统带通滤波器更好的效果。

但是，以上3 种方法如果单独用于滚动轴承故障诊断未必能够取得最好的效果，本研究提出一种基于谱峭度法和EMD 以及小波包分解联合应用的滚动轴承故障诊断的新方法，充分发挥这3 种方法在信号处理中的优势。具体的诊断流程如图1 所示。

图1 滚动轴承故障诊断流程图Fig.1 Flowchart of fault diagnosis of ball bearing

2 实际故障信号分析

为了验证本研究所提方法的可行性，使用Case Western Reserve University 轴承数据中心的SKF6205 滚动轴承故障数据进行诊断试验。所使用的数据是SKF6205 轴承的点蚀故障振动数据，其试验参数为:转速1 750 r/min，采样频率12 kHz。其中，外圈点蚀故障信号采样点数121 556，实际分析时取16 384 个点;内圈点蚀故障信号采样点数122 136，实际分析时同样取16 384 个点。经计算，外圈、内圈所对应的故障特征频率依次为104.6、157.9 Hz。

2.1 外圈点蚀故障信号

外圈故障信号的时域波形和幅频谱如图2 所示，可以看出，时域波形有周期性的冲击，但故障特征频率处的幅值十分微弱，基本上完全被噪声淹没，无法进行有效的故障诊断。

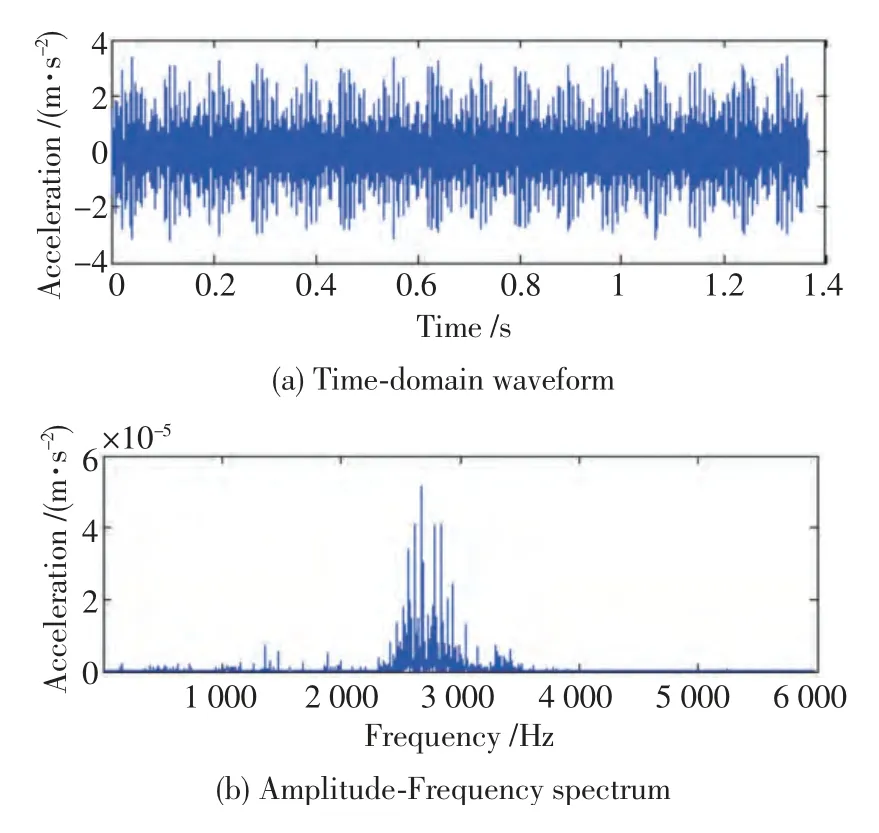
图2 外圈故障数据的时域波形和幅频谱Fig.2 Time-domain waveform and Amplitude-Frequency spectrum of outer race fault

为了提取故障特征，首先应用传统的包络解调方法，将原始信号通过一个低通FIR 滤波器(该滤波器阶数为398，截止频率为800 Hz)，滤波信号的包络谱如图3 所示。从图中可看到外圈的故障特征频率104.7 Hz 及其2 倍频210.2 Hz，但由于噪声的影响，其3、4 倍频等幅值微弱或较难发现，因此传统的包络解调法诊断效果并不理想。

图3 外圈故障信号的包络谱Fig.3 Envelope spectrum of outer race fault

接着应用本研究所提方法，对外圈故障信号作EMD 分解，得到13 个IMF，由于篇幅所限，这里只显示前3 个分量，如图4 所示。表1 所示的是外圈各IMF 与原信号的互相关系数以及各IMF的峭度值。这里只显示前5 项结果，其中原始信号的峭度值为3.993。

图4 外圈前3 个IMF 时域波形图Fig.4 First three Time-domain waveform of outer race's IMF

表1 外圈各IMF 与原信号的互相关系数及各自峭度值Table 1 IMFs'cross-correlation coefficient to outer race signal and its kurtosis estimation

由表1 可知，IMF1 的互相关系数为0.994，与原始信号的相关性最好，峭度值为4.010，说明IMF1 中含有较多的冲击特征，故可取IMF1 作为“合成信号”，求出该信号的快速谱峭度图(图5)，从中可以看出最大谱峭度处的峭度值为4.9，较原先的3.993 提高了很多，中心频率为5.5 kHz，带宽为1 kHz，可知最佳带通滤波器的范围为5 000～6 000 Hz，该频段刚好处于小波包分解树中的［1，1］节点(3 000～6 000 Hz)内，据此应用db10 小波对合成信号进行1 层小波包分解并重构［1，1］节点，该重构信号的包络谱如图6 所示，从中可以看出104.7 Hz 谱线处的幅值最大，而104.7 Hz 恰好是外圈的故障频率，并且在其2～5倍频处也出现了频率成分，与图3 相比，幅值明显增大，也即信噪比有了显著的提高，由此可以判断轴承外圈发生故障。

2.2 内圈点蚀故障信号

内圈故障信号的时域波形和幅频谱如图7 所示，可以看出，时域波形有周期性的冲击，但故障特征受噪声影响，信噪比太低，无法对故障进行有效诊断。

首先依旧应用常规的包络解调方法，将原始信号通过一个低通FIR 滤波器(该滤波器阶数为398，截止频率为800 Hz)并作包络谱如图8 所示。从图中可看到内圈的故障特征频率157.5 Hz 及其2 倍频314.9 Hz，但由于噪声的影响，其3、4 倍频等幅值微弱或较难发现，因此传统的包络解调法诊断基本上失效。

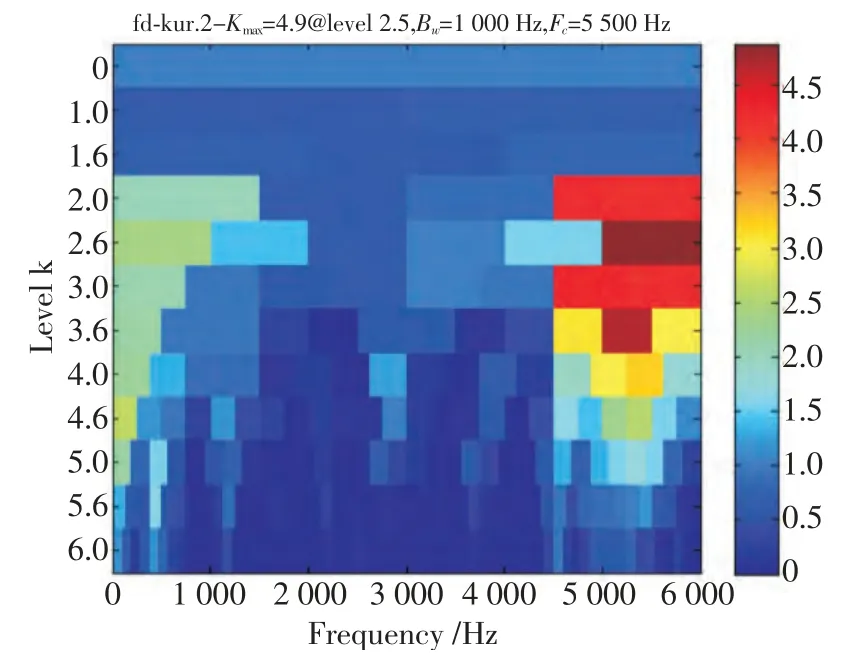
图5 外圈合成信号的快速谱峭度图Fig.5 Fast spectral kurtosis of compositive signal of outer race

图6 外圈故障信号的包络谱Fig.6 Envelope spectrum of outer race fault

图7 内圈故障数据的时域波形和幅频谱Fig.7 Time-domain waveform and Amplitude-Frequency spectrum of inner race fault

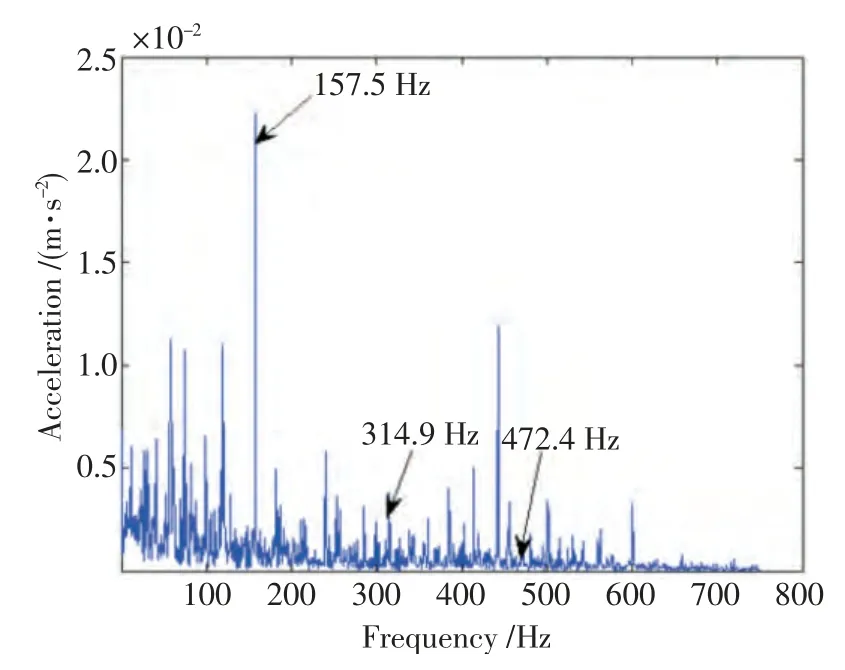
图8 内圈故障信号的包络谱Fig.8 Envelope spectrum of inner race fault

应用本研究所提方法，对内圈故障信号进行EMD 分解，得到14 个IMF，由于篇幅所限，这里只显示前3 个分量，如图9 所示。

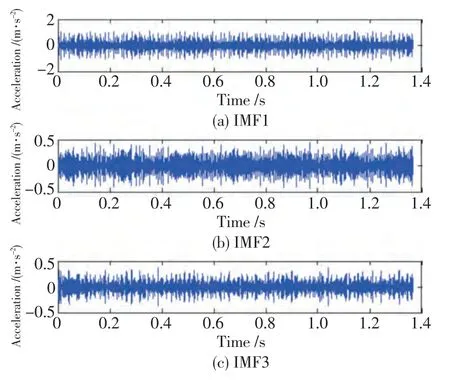
图9 内圈前3 个IMF 时域波形图Fig.9 First Three Time-domain waveform of inner race's IMF

表2 所示的是内圈各IMF 与原信号的互相关系数以及各IMF 的峭度值，这里只显示前5 项结果。

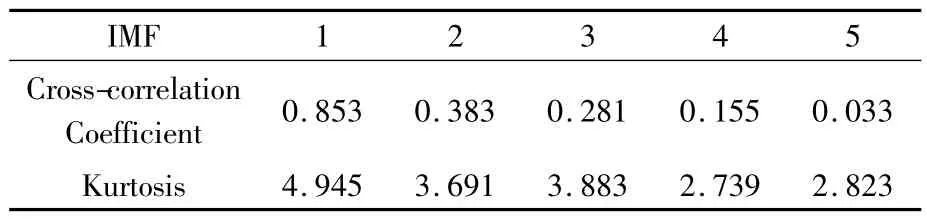
表2 内圈各IMF 与原信号的互相关系数及各自峭度值Table 2 IMFs'cross-correlation coefficient to inner race signal and its kurtosis estimation

由表2 可知，IMF1 与原信号的互相关系数较大且峭度值大于3，保留了原信号中最多的冲击特征，故可重构第1 个IMF，求出该合成信号的快速谱峭度图(图10)，从中看出中心频率为500 Hz，带宽为1 000 Hz，可知最佳带通滤波器的范围为0～1 000 Hz，该频段刚好处于小波包分解树中的［2，0］节点(0～1 500 Hz)内，据此应用db10 小波对合成信号进行2 层小波包分解并重构［2，0］节点，该重构信号的包络谱如图11 所示，从中可以看出幅值最大处的频率成分为157.5 Hz，恰好是内圈的故障频率，并且在其2 倍频(314.9 Hz)、3 倍频(472.4 Hz)、4 倍频(629.9 Hz)处也出现了明显的幅值，由此可以判断轴承内圈发生了故障。

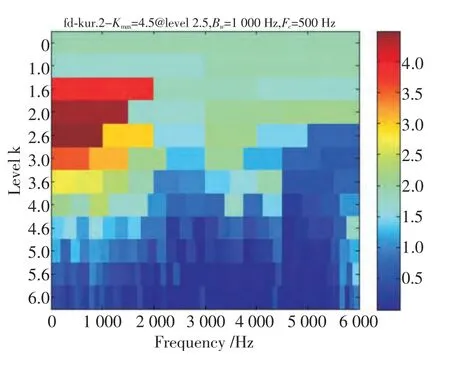
图10 内圈合成信号的快速谱峭度图Fig.10 Fast spectral kurtosis of compositive signal of inner race

图11 内圈故障信号的包络谱Fig.11 Envelope spectrum of inner race fault

3 结论

1)运用EMD 法，综合考虑各IMF 分量与原信号的相关系数及其峭度值，避免了选取若干IMF 进行包络解调的盲目性，突出了信号的高频共振成分，减少了低频干扰，提高了峭度值。

2)运用谱峭度法发现了故障特征最明显的频带，确定了提取故障特征所需的带通滤波器参数。

3)以谱峭度法确定的带通滤波器参数为依据，以db10 小波为工具，运用小波包变换成功地提取了滚动轴承的故障特征。

4)谱峭度、EMD 和小波包的相互结合，可以有效地诊断滚动轴承早期故障。通过分析实际故障信号，验证了本文所提方法的可行性。

［1］黄志坚，高立新，廖一凡，等.机械设备振动故障监测与诊断［M］.北京:化学工业出版社，2010:68-72.

［2］何正嘉，陈进，王太勇，等.机械故障诊断理论及应用［M］.北京:高等教育出版社，2010:167-169.

［3］李光，丛培田.基于共振解调的滚动轴承故障诊断的研究与实现［J］.机械工程师，2006(10):129-131.

［4］Huang N E，Shen Z，Long S R，et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and nonstationary time series analysis［J］.Proceedings of the Royal Society of London A Mathematical Physical and Engineering Series，1998，454(1971):903-995.

［5］杨宇，程军圣.机械故障信号的广义解调时频分析［M］.长沙:湖南大学出版社，2012:20-21.

［6］朱汉明.基于EMD 和共振解调的滚动轴承故障诊断方法研究［D］.上海:上海师范大学，2011:18-22.

［7］何岭松，李巍华.用Morlet 小波进行包络检波分析［J］.振动工程学报，2002，15(1):119-122.

［8］胡晓依，何庆复，王华胜，等.基于STFT 的振动信号解调方法及其在轴承故障检测中的应用［J］.振动与冲击，2008，27(2):82-86.

［9］Dwyer R.Detection of non-Gaussian signals by frequency domain kurtosis estimation ［C］.Acoustics，Speech，and Signal Processing，IEEE International Conference On ICASSP，Boston，1983，8:607-610.

［10］Antoni J.The spectral kurtosis:A useful tool for characterising non-stationary signals［J］.Mechanical Systems and Signal Processing，2006，20(2):282-307.

［11］Antoni J，Randall R B.The spectral kurtosis:Application to the vibratory surveillance and diagnostics of rotating machines［J］.Mechanical Systems and Signal Processing，2006，20(2):308-331.

［12］Antoni J.Fast computation of the kurtogram for the detection of transient faults［J］.Mechanical Systems and Signal Processing，2007，21(1):108-124.

［13］石林锁.滚动轴承故障检测的改进包络分析法［J］.轴承，2006(2):36-39.

［14］王冬云，张文志.基于小波包变换的滚动轴承故障诊断［J］.中国机械工程，2012，23(3):295-298.

［15］曾庆虎，邱静，刘冠军，等.基于小波相关滤波法的滚动轴承早期故障诊断方法研究［J］.机械科学与技术，2008，27(1):114-118.

［16］陈振华，赵二虎，胡怀辉.镁合金超声检测的相关增强小波去噪技术［J］.失效分析与预防，2012，7(2):69-72.

［17］胡红英，马孝江.基于局域波分解的信号降噪算法［J］.农业机械学报，2006，37(1):118-120.