基于一维泥沙数学模型的水库淤积与回水耦合研究

白瑞春

(温州广汇水利建设有限公司，浙江 温州 325011)

0 引言

水库在我国抗洪抗旱过程中发挥了巨大作用，全国地表供水量的1/3都由水库提供.库容是水库安全运行的重要保障，而水库泥沙淤积会导致库容损失，降低水库利用效率［1－3］.在各类水库淤积危害中，库尾泥沙淤积最为严重，由于此处远离坝前，因此难以对其进行有效冲刷.水库泥沙淤积还会引起回水抬高，进而引起淹没、内涝、土地盐碱化、洪水水位增加等灾害，因此研究水库淤积与回水耦合关系意义重大.研究表明，水库泥沙运动属于非均匀不平衡运动［4］.前苏联学者在20世纪30年代首先建立了一维不平衡泥沙输运方程，为后人的研究奠定了基础［5］.随后出现了水沙运动的二维数学模型，通过数值模拟得出了粒径大于0.1 mm的泥沙会在水库回水末端沉积［6－7］.基于国内外研究现状，一维、二维数学模型都已经得到广泛应用.一维模型适用于长河段河床变形研究;二维模型适用于泥沙运动沿水深、河宽变化不大的流动.结合水动力学、水库泥沙淤积理论，建立了一维非平衡泥沙输运数学模型并对其进行数值研究，得出水面线和淤积分布情况.并研究了淤积长度与回水长度、淤积厚度与回水抬升的耦合关系.

1 泥沙运动数学模型的建立

与水沙充分掺混的模型试验相比，数值模拟不受模型尺寸限制，可以通过改变初值条件、试验参数等计算多种方案下的泥沙输运规律.泥沙运动数学模型主要基于水沙运动规律，同时将数学模型作为研究手段.常用的数值模拟方法有一维不平衡泥沙模型和二维泥沙模型，本文主要通过一维非平衡泥沙输运数学模型对水库泥沙淤积与回水耦合关系进行研究.

依据圣维南定理，悬疑质运动采用一维不平衡输运方程进行计算［8］.悬疑质流动遵循连续性方程:

其中:A—河道断面面积，m2;

Q—河水流量，m3/s;

x—距离，m;

t— 时间，s.

流动还满足动量方程:

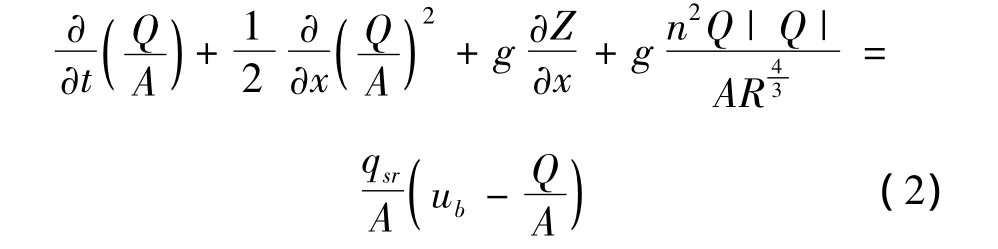
其中:Z—水位，m;g—重力加速度，m3/s2;

n—渠道粗糙系数，无量纲;

R—渠道的水力半径，m;

qsr—入口流量，m3/s;

ub—来流速度在x方向的分量，m/s.

非平衡泥沙输运方程为:

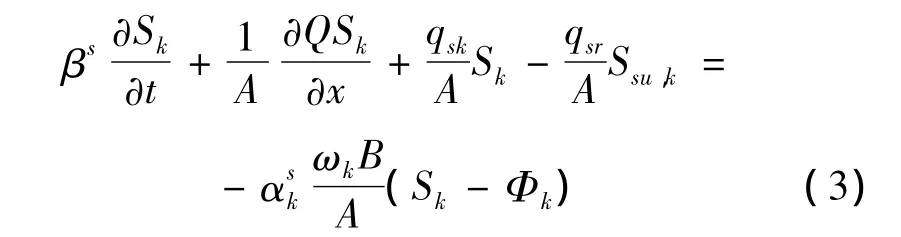
其中:β—泥沙浓度系数，无量纲;

Sk—断面平均泥沙浓度，kg/m3;

ωk—分组泥沙的沉降速度，m3/s;

qsk—出口流量，m3/s;

Ssu，k— 入口平均泥沙浓度，kg/m3;

B—河道断面宽度，m;

Φk—河道水流携沙能力，kg/m3.

水库河床变形方程为:

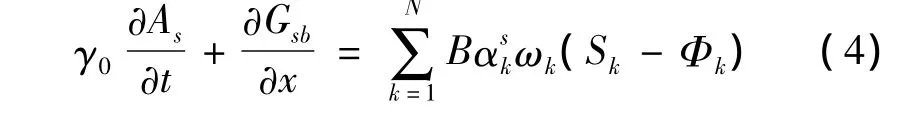
其中:γ0— 容重，kg/m3;

由此得出第k组泥沙的冲刷函数为:

其中:Pbk—沙床级配函数;

φk—混合沙的挟沙能力.

2 泥沙运动模型的求解

求解一维泥沙数学模型之前，首先需要确定其初始参数，主要参数有:初始粗糙率、泥沙沉降速率、挟沙能力系数;淤积物容重等.经过对试验对象进行分析，其底坡为J=7.5‰，因此取0～23 m的初始粗糙率为0.017，取23～60 m的初始粗糙率为0.013.假设颗粒直径为D，泥沙沉降速率按照经验公式计算得到:

泥沙容重 γs取2650 kg/m3;干容重采 γ取1325 kg/m3.选取一组典型工况，运用Preissmann四点隐式算法和有限差分法对一维泥沙模型进行求解，计算出水面线及淤积分布［6－7］.流量 Q 为0.02 m3/s，尾水水深 H 为 0.44 m，含沙量 S 取1 kg/m3，计算时间长度取7 h.7 h后的水位淤积地形情况(见图1).

图1 7 h后的水位淤积地形情况

由图1可以看出:经过7 h后，在沿程距离10～40 m出已经出现了明显的泥沙淤积.从试验结果来看，数值模拟结果与实测结果基本吻合.进一步分析，累计淤积量与沿程距离之间的关系，发现数值模拟得到的累积淤积量与测得的累积淤积量的偏差在10%以内.7 h后的累积淤积量与沿程距离之间的关系(见图2).

由图2可以看出，随着沿程距离的增加，累积淤积量先平缓上升，随后快速上升.当沿程距离达到40 m后，上升速度变得十分缓慢.实测数据与数值模拟得到的数据基本吻合，可见本文提出的一维泥沙模型可用于水库淤积与回水耦合研究.

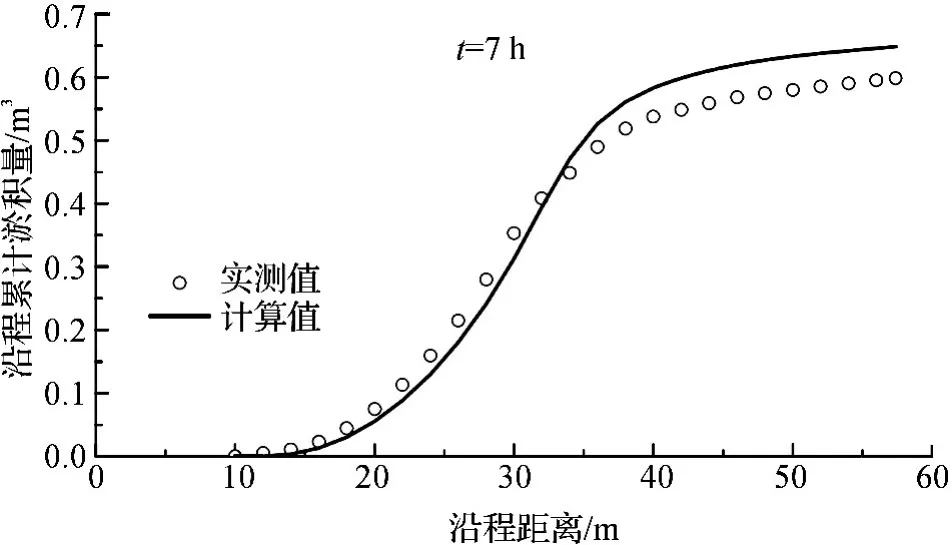
图2 累积淤积量与沿程距离的关系

3 水库淤积与回水耦合研究

由数学模型可以看出，影响淤积的因素很多，但回水抬升是导致水库淤积的主要原因.在河流上游修筑水库，库区水位抬升，导致水流速度降低，挟沙能力下降，大量的泥沙沉降到水库中，导致落淤区域出现回水抬升现象并促进泥沙的进一步淤积［9］.形成泥沙淤积—水位抬升—淤积加剧—回水抬升—再淤积的恶性循环.研究表明，水库淤积量的大小取决于相对坡比降Jc/J0和相对水深h/H.

其中Jc为淤积平衡比降;J0为原河床比降;H为淤积前的坝前深度;h淤积平衡后的坝前深度.

3.1 淤积长度与回水长度

若底坡为 J=7.5‰，Q 为 0.025 m3/s，尾水水深H为0.45 m，含沙量S取2 kg/m3，沙粒直径取0.1 mm，计算中的零点为水库大坝位置.首先计算淤积末端与回水末端随时间的变化(见图3).其中图3上边的曲线为回水末端，下边的曲线为淤积末端.

由图3可知，淤积末端与回水末端随时间的变化规律基本相同，但是淤积起始点较回水起始点更靠近水库大坝.在淤积初步平衡以前，淤积回水末端向上游增长的更快些;但淤积初步平衡后，两条曲线的增加速度都变得十分缓慢.由于淤积末端和回水末端的增加速度基本一致，因此对其试验数据做线性拟合，得到计算式:

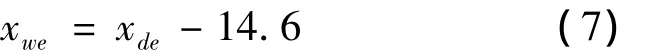
其中:xwe—回水末端到坝前的距离，m;

xde—淤积末端到坝前的距离，m.

泥沙堆积形成的三角洲洲面淤积长度与回水长度间也存在耦合关系.基于泥沙数学模型对其进行研究，得出泥沙三角洲的情况(见图4).其中图4上边的曲线为回水长度，下边的曲线为洲面淤积长度.

图3 淤积末端与回水末端随时间的变化

由图4可知，三角洲洲面淤积长度的增长趋势与回水长度基本一致，两条曲线呈近似平行关系.回水长度值总是大于洲面长度，在淤积初步平衡之前，两条曲线的增长速度很快，增加趋势为近似线性增加;到达初步平衡后，二者增长速度逐渐降低.对二者的试验数据进行线性拟合，得出本工况回水长度的经验计算式:

其中:lw—回水长度，m;

lde—三角洲洲面淤积长度，m.

3.2 淤积厚度与回水抬升

在研究淤积长度与回水长度耦合的基础上，本节将进一步研究淤积厚度与回水抬升的关系.研究之前，首先定义无量纲距离x/L0，x为到坝前的距离，L0为静回水长度，本文试验中的静回水长度取47.1 m.表1给出了距坝距离、无量纲距离、沿程距离对照表.

表1 沿程、无量纲距离对照表

采用无量纲距离计算各个断面淤积厚度与水位抬升高度之间的关系，将计算数据绘制成曲线(见图5).

计算结果显示，淤积厚度与水位抬升高度的关系十分复杂.图中:直线adc代表该断面淤积厚度与水位抬升高度的增加完全相同;曲线bde为初步淤积平衡分界线;直线aef表示淤积三角洲洲头位置到达各个断面的时间.由直线adc和曲线bde将图5划分为 A、B、C1、C2四个区域.

区域A为各个起始淤积点下游断面未达到初步平衡时的淤积情况.由图5中可知，各点未达到淤积平衡时，淤积厚度与回水抬升曲线基本与直线adc平行，说明其斜率近似为1.即A区域内各点淤积厚度对回水的贡献基本相同.

图5 淤积厚度、水位抬升高度关系曲线

区域B为各起始淤积点下游断面达到初步平衡后的淤积情况.从图中可以看出，淤积初步平衡后，各点淤积厚度与回水抬升曲线的斜率自左向右依次降低，直到淤积厚度最大处的斜率接近于0.究其原因，此处的坝前深度远大于淤积厚度，泥沙淤积对水位的影响可以忽略.

区域C1为各起始淤积点上游断面达到初步平衡前的淤积情况.区域C1内的淤积规律与区域A相似，此区域各点淤积厚度对回水的贡献基本相同，关系直线的斜率接近1.

区域C2为各起始淤积点上游断面达到初步平衡后的淤积情况.区域C2内的淤积规律与区域B相似，但是上游断面淤积厚度对水位抬升的影响较大.

4 结语

库容是水库安全运行的重要保障，而水库泥沙淤积会导致库容损失，降低水库利用效率.水库泥沙淤积还会引起回水抬高，进而引起淹没、内涝、土地盐碱化、洪水水位增加等灾害，

结合水动力学、水库泥沙淤积理论，建立了一维非平衡泥沙输运数学模型并对其进行数值研究，得出水面线和淤积分布情况.并研究了淤积长度与回水长度、淤积厚度与回水抬升的耦合关系.研究表明:

(1)随着沿程距离的增加，累积淤积量先平缓上升，随后快速上升.当沿程距离达到40 m后，上升速度变得十分缓慢.实测数据与数值模拟得到的数据基本吻合，可见一维泥沙模型可用于水库淤积与回水耦合研究.

(2)淤积末端与回水末端随时间的变化规律基本相同，但是淤积起始点较回水起始点更靠近水库大坝.三角洲洲面淤积长度的增长趋势与回水长度基本一致，两条曲线呈近似平行关系.

(3)淤积厚度与水位抬升高度的关系十分复杂，本文将其分为4个区域，更清晰的讨论了淤积厚度与水位抬升在不同阶段的关系.

［1］卢金友，黄 悦.三峡水库淤积计算预测与原型实测结果比较分析［J］.长江科学院院报，2013(12):1 －6.

［2］曹慧群，李青云，黄 茁，等.我国水库淤积防治方法及效果综述［J］.水力发电学报，2013(6):183－189.

［3］欧应钧，封光寅，赵学峰.丹江口水库泥沙调度方式探讨［J］.人民长江，2014(2):82 －85.

［4］张小帅，张耀哲.基于MATLAB的非均匀悬移质不平衡输沙计算［J］.人民黄河，2014(11):26－29.

［5］李继伟.梯级水库群多目标优化调度与决策方法研究［D］.保定:华北电力大学，2014.

［6］邓春艳，吴卫民，夏军强.岩滩水库泥沙淤积计算数学模型［J］.武汉大学学报:工学版，2013(1):19 －25.

［7］谢金明，吴保生，刘孝盈.水库泥沙淤积管理综述［J］.泥沙研究，2013(3):71－80.

［8］谢 龙.三峡变动回水区末端段复合水动力条件分析及对泥沙输移的影响［D］.重庆:重庆交通大学，2013.

［9］卢 克.河口悬浮泥沙浓度遥感反演模型的探讨［J］.浙江水利水电专科学校学报，2012，73(3):63－65.