转移率部分未知的Markov跳变神经网络的稳定性

刘 月



转移率部分未知的Markov跳变神经网络的稳定性

刘 月

（铁岭师范高等专科学校理学院 辽宁铁岭 112000）

研究了具有 Markov 跳跃和区间时变时滞神经网络系统的稳定性问题。此类Markov跳变神经网络系统的转移概率矩阵元素部分未知，因而更具有一般性。通过建立新颖的增广Lyapunov泛函和应用反凸组合技术，得到了含有转移概率部分未知的 Markov 跳变神经网络的稳定准则。提出的方法不需要知道转移概率矩阵中未知元素的任何信息，增加了结果的使用范围。同时，得到的稳定性准则依赖于时滞的上下界。最后, 通过数值仿真验证了所得结果的正确性。

转移率部分未知 神经网络Markov 跳变 反凸组合技术

神经网络已应用到各个领域，比如：联想记忆、图像处理、组合优化、模式识别[1,2]，因此受到人们的广泛关注。由于时滞对神经网络的稳定性有很大的影响，因此，与变时滞相关的神经网络系统稳定性问题受到广泛的研究。

在实际应用中，由于模型误差、外部扰动、参数变化等因素无法消除，系统常常受到各种随机因素的干扰，从而使随机系统的研究得到了广泛关注。关于马尔科夫系统问题的相关研究中，大多假设转移概率完全已知[3,4]，然而在实际工程应用中，完全得到转移概率的全部信息十分困难，因此，对转移概率部分未知的 Markov 系统的研究是十分必要的。目前，大多数研究是针对转移概率部分未知的 Markov 线性系统的，然而，转移概率部分未知随机神经网络的研究不多。文献[5]研究了转移概率部分未知的不确定 Markov 跳变线性系统的鲁棒稳定问题。文献[6]和[7]分别应用不同的方法研究了转移率矩阵含有部分信息随机 Markov 跳跃系统的稳定性问题。以上这几个文献，虽然系统跳跃过程的转移概率为部分未知的，但是这些系统都是线性的。另外，神经网络系统的实现过程中，由于放大器切换速度的影响，会有时滞产生[8]。然而，时滞的存在可能会引起系统的不稳定性[9]。因此，研究时滞神经网络是很有必要的。文献[10]分析了一类具有时变时滞和不确定性的细胞神经网络全局渐近稳定性问题.。文献[11]通过建立合适的Lyapunov泛函，研究了具有时变时滞的模糊双曲神经网络的稳定性问题。这几个文献研究了时滞神经网络问题，没有考虑随机现象。文献[12]研究了转移率矩阵完全已知的 Markov 跳变神经网络的鲁棒稳定性问题。文献[13]研究了转移率部分未知的Markov 跳变神经网络稳定性和同步问题。文献[14]研究了含有转移率部分未知的Markov 神经网络有限时间有界性问题。虽然这两个文献研究了转移率部分未知神经网络系统问题，然而还有很大的提升空间。不同于以上方法，在本文中给出了新颖的增广Lyapunov泛函和应用反凸组合技术，得到了新的稳定性的准则。

基于以上研究成果，本文研究了一类具有转移概率部分未知的 Markov 跳变时变时滞神经网络的随机稳定问题，通过构造新的增广的Lyapunov泛函，利用反凸组合技术，给出了系统均方渐近稳定的准则，所得结果与以往相比更具有一般性和实用性，仿真实例证明了结果的可行性和有效性。

1 模型描述和预备知识

考虑如下具有时变离散时滞和分布时滞的Markov 跳变神经网络：

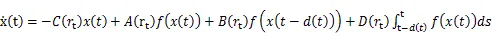
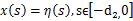
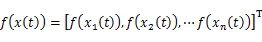
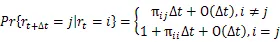
在文中，Markov 跳变的转移概率为部分未知的，且系统 (1) 的N个模态转移率矩阵表示为：

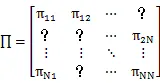
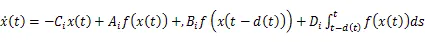
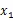
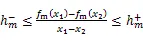
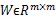
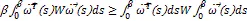
引理2[17]Rm→R在开子集有正值，且R，则定义在上，f的反凸组合满足下面式子：

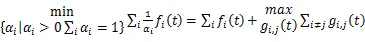
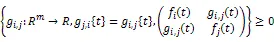
2 主要结果

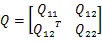
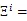
(6)

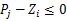
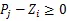
其中，

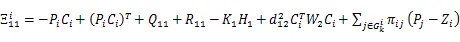
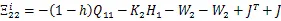
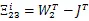
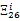
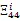
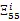
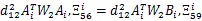
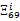
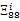
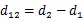
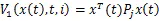
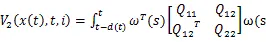
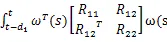
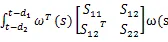
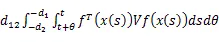
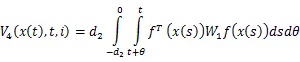
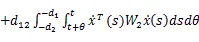
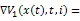
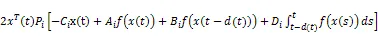
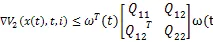
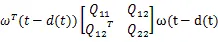
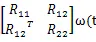
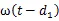
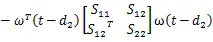
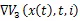
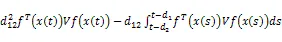
由式(16)和引理1，可得(17)

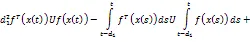
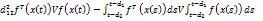
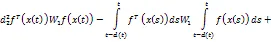
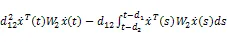
根据引理2中的反凸组合技术，可以得到，

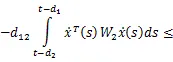
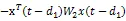
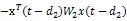
根据假设1，可以的到下面这些不等式。

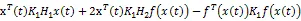
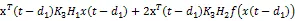
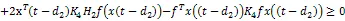
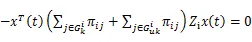
联合(10)~ (21)，我们可以得到

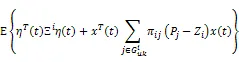
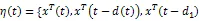
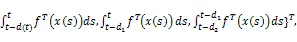
注１：与文献[1,2,8,10－15]相比，本文研究了时变时滞神经网络的稳定性问题，不但考虑了随机现象，而且还考虑了转移率部分未知的情况，从而扩展了在实际生产中的使用范围，具有更小的保守性。此外，利用增广的Lyapunov泛函，增加了线性矩阵不等式解的灵活性。同时，利用反凸组合技术减少了保守性。

3 数值仿真

考虑具有三个模态连续Markov跳变的时滞神经网络系统：

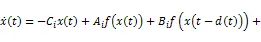
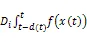
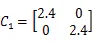
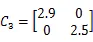
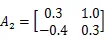
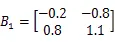
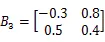
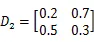
转移概率矩阵为：

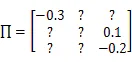
其中，“？”表示转移概率矩阵中无法获得的转移率。

假设初始值：

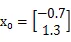
同时根据假设1，可以得到：

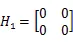
通过MATLAB中的LMI工具箱，求解定理1，我们可以得到如下可行解

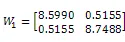
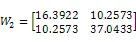
图１为 Markov跳变时滞神经网络系统的三个模态跳变曲线，图２为Markov跳变时滞神经网络系统的状态曲线图，我们可以看到系统收敛到原点。仿真图形如下。

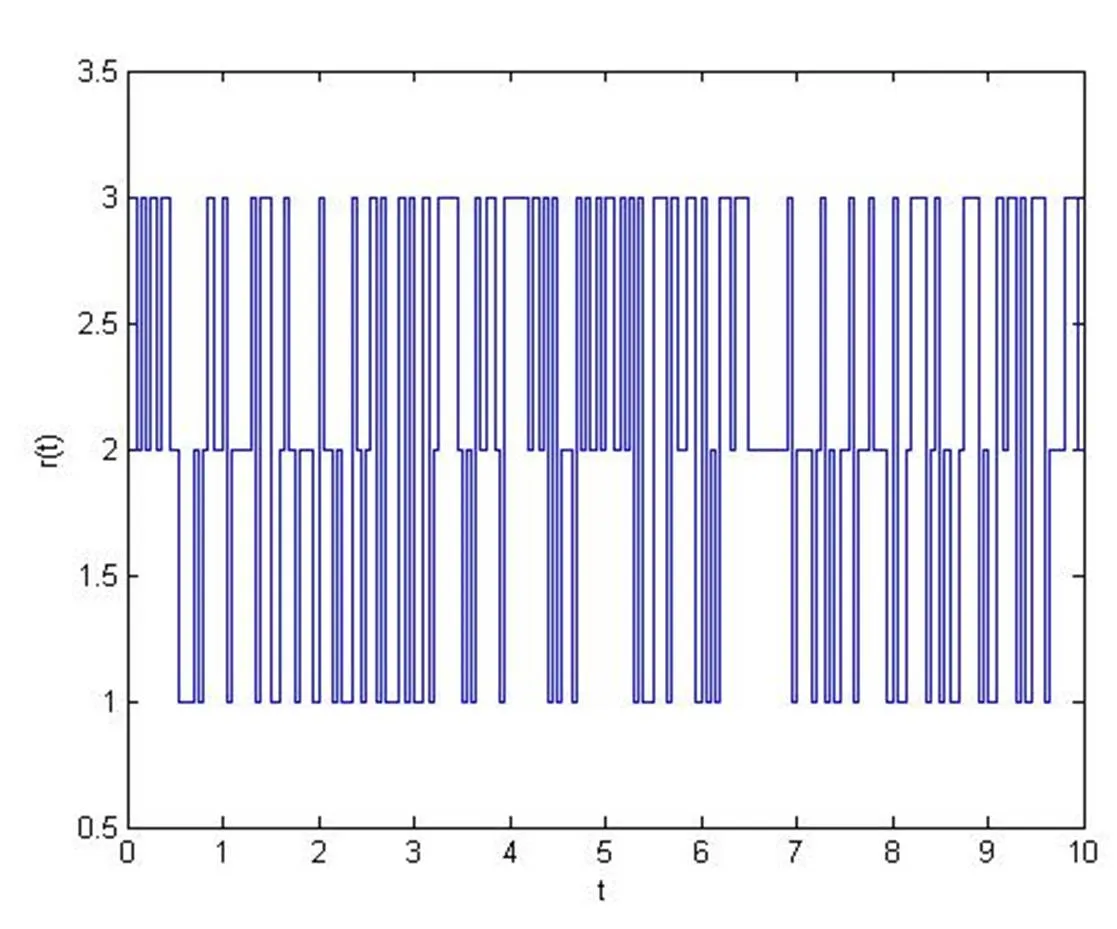
图1 系统(23)式的三个模态跳变曲线

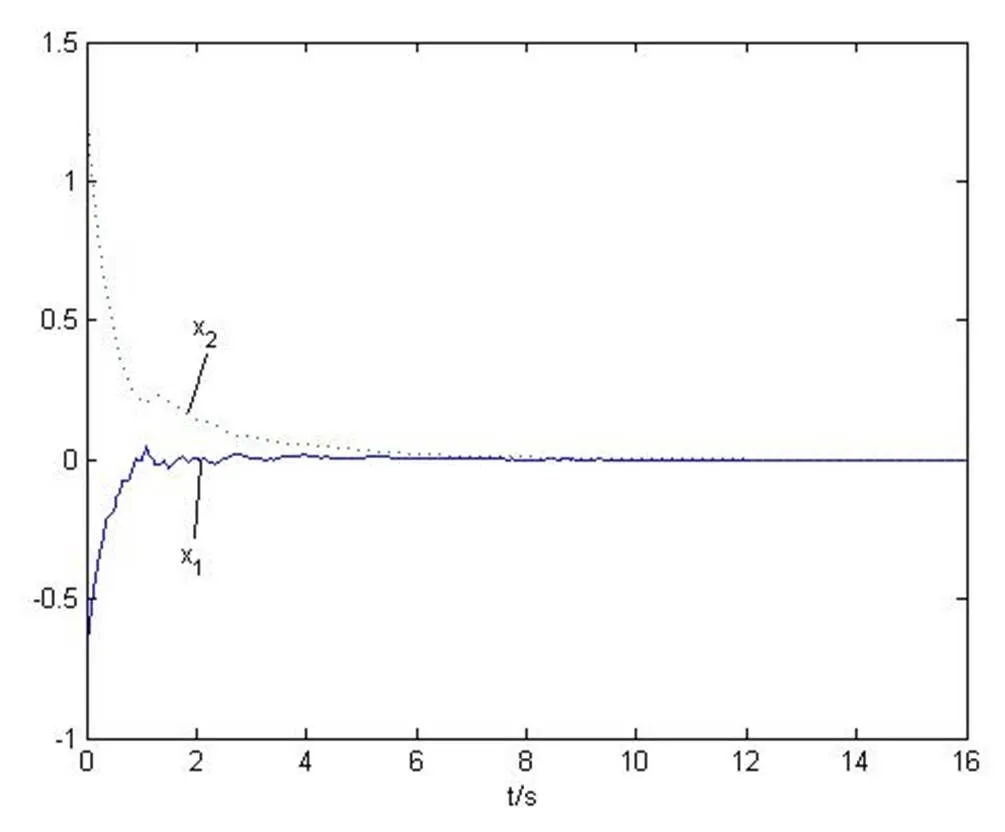
图2 Markov跳变时滞神经网络系统(23)的状态响应曲线

4 结语

通过建立增广的Lyapunov泛函和应用反凸组合技术，得到了含有转移概率部分未知的 Markov 跳变神经网络的稳定准则。目前，具有转移率部分未知Markov 跳变区间时变时滞神经网络随机稳定性的研究相应成果较少，与已有的转移概率完全已知的文献相比，本文的方法增加了系统在实际中的运用范围，更加接近于实际存在的系统模型。数值仿真说明了方法的可行性和有效性。

[1] Arik S. Stability analysis of delayed neural networks[J]. IEEE Trans. on Circuits and Systems I:Fundamental Theory and Applications,2000,47(7):1089–1092.

[2] CAO Ji-de,WANG Jun. Global asymptotic and robust stability of recurrent neural networks with time delays[J]. IEEE Trans. on Circuits and Systems I: Regular Papers, 2005,52(2):417–426.

[3] DONG Jiu-xiang, YANG Guang-hong．Robust H2 control of continuous-time Markov jump linear systems[J]. Automatica,2008,44(5):1431-1436．

[4] WU Zheng-guang, SHI Peng, SU Hong-ye, CHU Jian. Stochastic synchronization of Markovian jump neural networks with time-varying delay using sampled data[J]. IEEE Trans. on Cybernetics,2013,43(6):1796-1806.

[5] 钟向楠，王占山，张化光.转移概率部分未知的不确定Markov跳变系统的鲁棒镇定[J].吉林大学学报,2012,42(6):1558-1562.

[6] 盛立,高明.转移概率部分未知的随机Markov 跳跃系统的镇定控制[J].控制与决策,2011,26(11):1716-1720.

[7] ZHANG Yan, HE Yong, WU Min, ZHANG Jie. Stabilization for Markovian jump systems with partial information on transition probability based on free-connection weighting matrices[J],Automatica, 2011,47:79-84.

[8] 刘国权,周书民.一类含有时变时滞的不确定中立型Hopfield 神经网络的鲁棒稳定性判据[J].自动化学报,2013,39(9):1421-1430.

[9] WANG Gang, YANG Dong-shen, ZHAO Qing-qi.Delay-dependent fuzzy hyperbolic model based on data-driven guaranteed cost control for a class of nonlinear continuous-time systems with uncertainties[J]. Mathematical Problems in Engineering,2012,780740:1-17.

[10] 宫大为,冯健,刘金海.带有不确定性的时变时滞神经网络渐近稳定性分析[J].东北大学学报,2010,31(3):313-316.

[11] WANG Gang, ZHANG Hua-guang, CHEN Bin, et al. Fuzzy hyperbolic neural network with time-varying delays[J].Fuzzy Sets and Systems, 2010,161(19): 2533-2551.

[12] 盛立,杨慧中.一类Markov 跳变神经网络的时滞相关鲁棒稳定性[J].系统工程与电子技术,2009,31(11):2698-2702.

[13] MA Qian, XU Sheng-yuan, ZOU Yun. Stability and synchronization for Markovian jump neural networks with partly unknown transition probabilities [J].Neurocomputing,2011, 74:3404-3411.

[14] LI Liang. Finite-time boundedness for a class of delayedMarkovian jumping neural networks with partly unknown transition probabilities[J],Abstract and Applied Analysis, 2014:1-8,Article ID 597298.

[15] LIU Yu-rong, WANG Zi-dong, LIU Xiao-hui. Global exponential stability of generalized recurrent neural networks with discrete and distributed delays[J].Neural Networks,2006,19(5):667-675.

[16] GU Ke-qin, Kharitonov V L, CHEN Jie. Stability of time-delay systems[M].Boston: Birkhäuser,2003.

[17] Park P, Ko J W, Jeong C. Reciprocally convex approach to stability of systems with time-varying delays[J]. Automatica,2011,47(1):235-238.