考虑工件变形因素的曲轴磨削轨迹建模研究

肖 蓉



考虑工件变形因素的曲轴磨削轨迹建模研究

肖 蓉

（上海机床厂有限公司 上海 200093）

根据曲轴切点跟踪磨削的基本运动模型，分析影响曲轴连杆颈圆度误差的因素，建立考虑工件变形因素的曲轴连杆颈磨削轨迹模型，并以生产实例结合理论分析进行说明。通过对已加工曲轴连杆颈进行了圆度误差的测量，推导曲轴弹性变形量的函数，进而建立实际误差补偿模型，以提高待加工曲轴零件的精度。

曲轴 切点跟踪 运动模型 误差补偿

曲轴作为发动机的关键零部件之一，其性能及精度直接关系到该动力驱动部件的整体性能[1]。近年来，随着磨削技术的不断发展，越来越多的曲轴磨削都采用了切点跟踪磨削技术。该技术通过主轴颈旋转和砂轮的联动完成每段曲轴颈的磨削加工，是一种非圆磨削方法，不仅大幅减少了曲轴装夹与调整的辅助时间，还消除了传统加工方法（偏心装夹法）中多次装夹定位误差的影响，但由于存在受力弹性变形、联动误差的影响，会产生一定的圆度误差。

1 切点跟踪磨削基本数学模型

切点跟踪法磨削曲轴连杆颈是通过数控系统控制曲轴旋转(轴)和砂轮横向进给(轴)的联动来实现的。连杆颈切点跟踪磨削运动如图1所示，曲轴连杆颈绕主轴颈中心O旋转，砂轮沿轴作往复跟踪运动，实现曲轴连杆颈的磨削，磨削点坐标的轨迹方程为[2]：

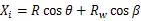
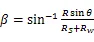
由图1中的几何关系可以推导出连杆颈切点跟踪磨削中砂轮中心的运动方程为（OOs的距离）：

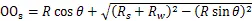
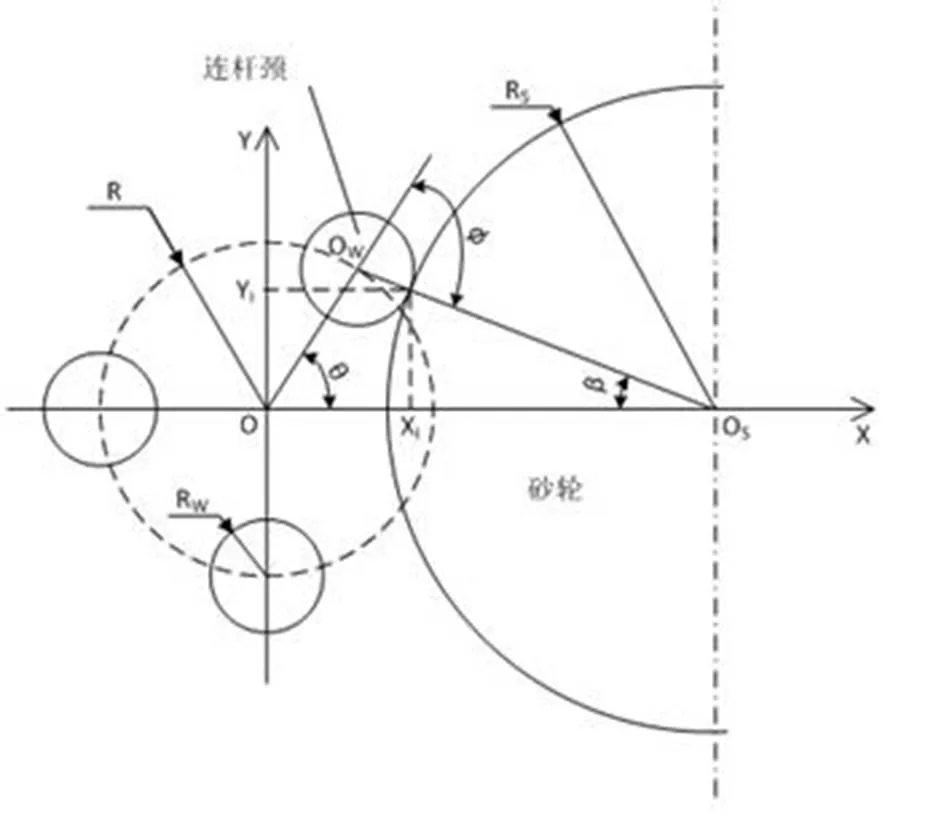
图1 曲轴切点跟踪磨削运动示意图

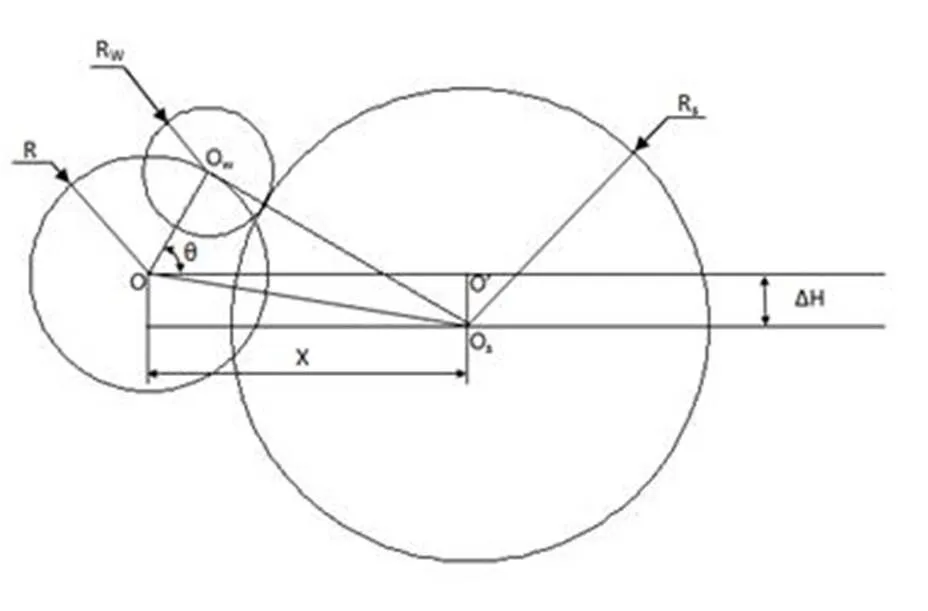
图2 存在安装高度误差的曲轴磨削模型

2 曲轴连杆颈圆度误差影响因素

曲轴切点跟踪磨削中，砂轮同曲轴连杆颈磨削时的相对运动关系类似普通外圆磨削过程。普通外圆磨削中，由于工件匀速转动，砂轮架在工件径向上做匀速进给运动，这样即使在磨削力和惯性力的作用下，砂轮架的进给误差和机床的变形只会影响工件的尺寸精度，对工件加工表面圆度误差的影响很小，而尺寸误差可以通过调整给定砂轮架进给位置来补偿。但在实际机床联动控制中，切点跟踪磨削的相对运动过程复杂，控制难度大。由于曲轴和砂轮的大惯量以及磨削受力的影响，曲轴转动(轴)和砂轮进给(轴)之间的联动精度会受到影响，所以连杆颈的尺寸精度和位置精度都无法保证。

在切点跟踪磨削过程中，曲轴连杆颈和砂轮中心的位置误差对加工出的连杆颈表面各点半径精度造成不一致的影响，从而加大了连杆颈圆度误差。为了减小曲轴连杆颈圆度误差，必须分析影响曲轴连杆颈和砂轮架中心之间相对位置关系的误差因素，并寻找出有效的补偿方法。

影响曲轴切点跟踪磨削精度的主要因素有，磨削过程中作用力引起的曲轴连杆颈回转中心弹性变形和曲轴旋转与砂轮纵向进给的联动误差。

在磨削力和惯性力的作用下，曲轴受力会产生弹性变形，导致曲轴连杆颈的中心在各磨削位置时发生偏移，即产生如图3所示的、量，进而引起圆度误差。

曲轴旋转与砂轮进给的联动误差主要影响连杆颈的尺寸精度和圆度误差，其中尺寸精度主要在R值上补偿，可以实际测量出直接反映在R上，圆度误差则等效在、上。

3 考虑工件变形因素的曲轴磨削轨迹建模

如图3所示，连杆颈受力变形后其中心由O变为 O'，砂轮中心由O变为O'，规定图示的、为变形量的正方向，反之为负。

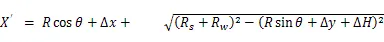
4 误差分析与补偿

求解加入变形量后的连杆颈磨削运动方程，关键在于求出变形量、。变形量、的确定一般有两种方法：实际测量和软件仿真分析。目前一种较先进的实际测量手段叫做跟踪测量技术，这种误差确定方式获得的测量结果可信度高，但要大量的技术、资金投入；而软件仿真分析，其结果的可信度相对有所下降，但它是通过计算机软件实现，可以免除硬件投入及其设计制造装配所需的长周期，比较常用的如ANSYS软件分析。

由于曲轴连杆颈的加工误差主要表现为圆度误差，而圆度误差的测量方法相对比较简单。采用已测得的圆度误差值对、进行推导，得到圆度误差和弹性变形（、）的关系。

如图4所示为曲轴磨削过程连杆颈受力分析示意图，弹性变形公式为：

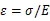
图4 磨削过程受力分析示意图

曲轴连杆颈的主要受力是切向磨削力F和正向磨削力F，他们的大小是受砂轮进给的力、连杆颈的旋转惯性力和力偶以及其他多种因素共同作用的结果，所以难以分析，但他们的方向是可以确定的，分别是磨削点的切线和法线方向上。而且切向磨削力Ft和正向磨削力F之间还存在如下关系：

4.2 曲轴磨削实际补偿计算模型

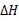
图5 曲轴连杆颈圆度误差示意图

圆度误差主要是由曲轴受力产生弹性变形引起的，图中曲线一直在不停的波动是由于曲轴内部组织的不均匀性，其弹性模量E在不断变化以及机床振动引起的，因此要分离出只有弹性变形引起的圆度误差，求解（、）以对砂轮实时进给量进行理论补偿。

将曲轴连杆颈角度（弧度值）和圆度误差的对应值输入matlab，绘制散点图，然后再通过matlab求出它们之间的回归函数，如图6所示。

图6 曲轴连杆颈圆度误差散点图及其回归函数

设回归函数为() =*sin(*+)，matlab具体计算结果如下：

General model:

() =*sin(*+)

Coefficients (with 95% confidence bounds):

=0.001868 (0.001808, 0.001929)

=2.037 (2.02, 2.055)

=0.3268 (0.261, 0.3925)

Goodness of fit:

SSE: 0.0009655

R-square: 0.7202

Adjusted R-square: 0.7198

RMSE: 0.0008194

得到的圆度误差近似函数为：

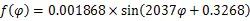
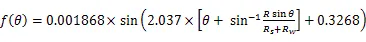
曲轴连杆颈每个磨削点的弹性变形都发生在曲轴连杆颈和砂轮的连心线上，由图4中的几何关系将弹性变形分解到,轴上，得到∆、∆。

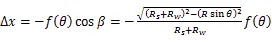
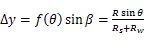
利用matlab进行函数图像分析，可以得到、，它们与主轴（轴）旋转角度的关系，分别如图7、图8所示。

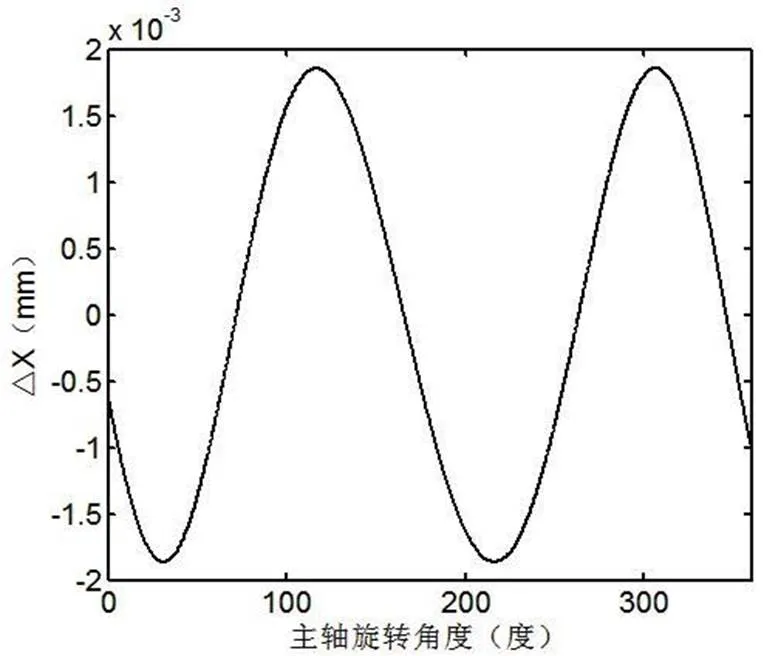
图7 ∆x与θ关系曲线图

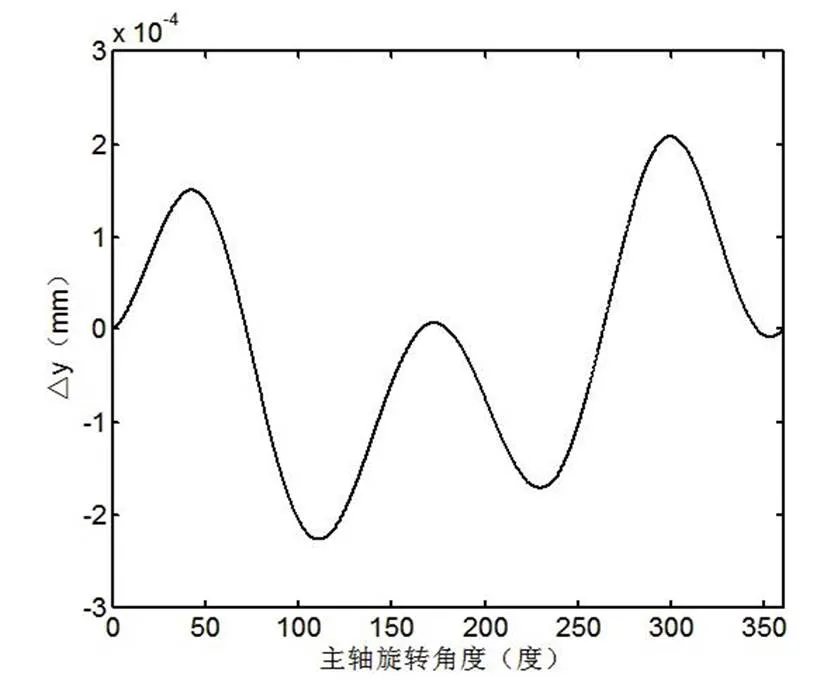
图8 ∆y与θ关系曲线图

将∆与∆代入公式（6）即可得到误差补偿后的砂轮中心运动轨迹。补偿前后的与主轴（轴）旋转角度之间的关系如图9所示，其中（a）为整体曲线对比图，（b）为（a）中圈出部分的局部放大效果图，可以看出补偿前后的差异。

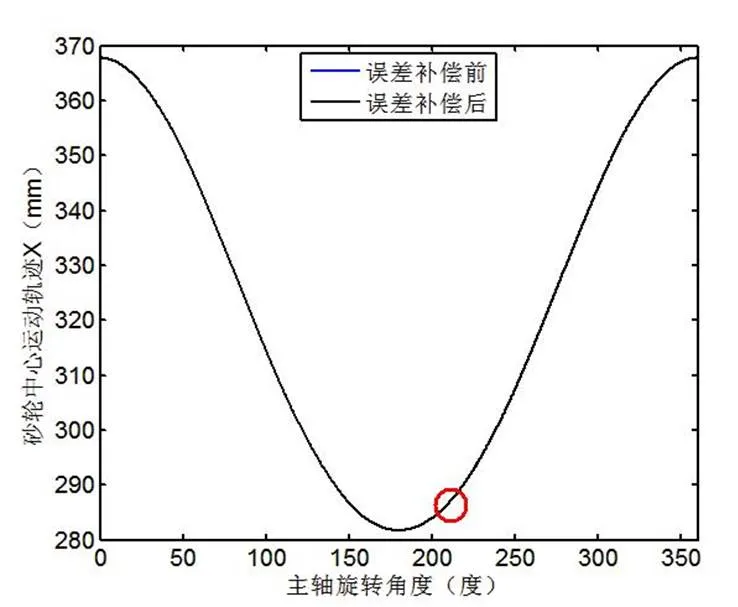
（a）整体曲线对比

（b）局部放大

图9 误差补偿前后的与关系曲线图

结语

分析了磨削加工中影响曲轴圆度误差的一些重要因素，在磨削过程中，曲轴受外力作用产生弹性变形、曲轴旋转与砂轮进给的联动误差，它们的主要作用形式等效为∆、∆。

在实际磨削中，运用误差补偿，一定程度上提高了曲轴磨削的圆度，同时，还提高了加工效率。

[1] 许第洪.切点跟踪磨削法核心技术的研究[D].长沙：湖南大学,2004.

[2] 李静.提高大型曲轴切点跟踪磨削轮廓精度的关键技术研究[D].上海:上海大学,2011.

[3] 吴钢华.曲轴非圆磨削轨迹控制关键技术研究[D].上海:上海大学,2006.

[4] 汪学栋,房小艳.切点跟踪曲轴磨床磨削力的计算公式分析[J].精密制造与自动化,2012(3):17-19.

[5] 田应仲.曲轴非圆磨削表面几何形状误差及其在线测量方法的研究[D].上海:上海大学,2007.

[6] 罗红平.切点跟踪磨削法磨削理论及若干关键技术研究[D].长沙:湖南大学,2002.