基于改进PERT的输水隧洞施工进度风险分析

洪 坤，余 佳，刘 震，赵梦琦，毕 磊

(天津大学水利工程仿真与安全国家重点实验室，天津300072)

输水隧洞施工是一个随机动态变化的过程［1］，施工中存在的诸多不确定风险因素不仅会对工序持续时间造成影响，还会导致风险处理活动的增加，使原有工序间的逻辑关系发生变化，进一步影响施工进度。因此，为确保工程进度目标的实现，对隧洞施工进行风险分析具有重要意义。PERT作为项目进度风险分析的重要方法，在工程施工行业已得到广泛的应用。该方法认为各活动时间服从β分布，通过最乐观时间a、最可能时间m、最悲观时间b三时估计值来计算活动时间的均值和方差，最终求解项目关键线路和完工概率。在PERT方法研究方面，国内外学者开展了一系列工作。Keeefr．D．L等(1993)归纳总结出五种PERT网络活动时间均值和方差的计算方法，并对这些方法在活动时间估计方面的误差进行了分析［2］。刘武等(2008)基于PERT网络分布的假设，在分析常规三时估计方法不足的条件下，采用限定三时估计及拟合方差最小模型，分别对常规三时估计方法及常规β分布函数参数进行了改进［3］。José等(2011)在分析原有β分布活动时间计算的基础上，通过构造一个与三时估计值相关的调整变量C(δ)对活动时间的方差计算进行调整，使得活动时间的估算更加合理［4］。蔡开玺和唐爱兵(2011)针对经典PERT在β分布时间估计方面的缺陷，探讨了基于数据统计和定额计算法的“综合估算方法”，该方法按照三点估计法对于工序时间进行估计，并借鉴统计资料进行计算，以实现PERT方法计算精度的提高［5］。王涛和蔡建峰(2012)针对经典PERT方法假设条件苛刻，β分布活动时间方差估算公式固定单一，不能随实际情况变化而变化的局限性，仅保留一个PERT假设条件，综合考虑a、b、m三个时间参数对于方差计算的影响，对活动时间方差计算公式进行改进［6］。综上所述，国内外针对工程项目施工进度开展的PERT网络研究，多集中于对施工活动时间单方面的分析，未考虑工序逻辑关系对施工进度的影响，致使施工进度风险分析结果可靠性不足。同时，现有研究所得的活动时间多为基于三时估计的特定β概率分布，难以满足实际施工中活动时间服从不同分布的要求。因此，本文结合输水隧洞施工特点，并考虑经典PERT网络研究的不足，从逻辑关系和活动时间两个方面对经典PERT进行了改进，开展输水隧洞施工进度风险分析。具体来说，首先从风险事件的角度出发，将定性分析与定量分析相结合，探讨逻辑关系的变化对施工进度的影响;其次，在三点估计值的基础上引入四分位数作为第四个参数，提出了不同β分布形式的确定方法;最后，运用 Monte Carlo仿真法对改进PERT网络进行求解，实现对输水隧洞施工进度风险更加全面的分析，为工程施工进度管理提供了科学的依据。其总体结构如图1所示。

图1 基于改进PERT的输水隧洞施工进度风险分析

一、输水隧洞施工进度风险体系

输水隧洞施工条件复杂，施工过程中面临着诸如复杂地质条件、施工技术水平、施工机械配置等风险因素［7］，致使工序间逻辑关系和活动持续时间受到一定影响，进一步造成施工进度的变化。风险因素对工序间逻辑关系和活动持续时间的影响主要体现在:1)施工过程中存在着涌水、断层、衬砌支护不合格、施工机械故障等安全隐患，一旦发生此类风险事件，则需采用排水、打锚杆和固结灌浆、重新衬砌支护、机械故障排除等相应的风险处理措施。相对于原有的施工进度计划，这些风险处理活动可视为网络进度计划中的新增工序，从而使原有工序间逻辑关系发生变化。2)开挖过程中的岩性条件、施工队熟练程度、施工机械工作效率等因素将影响施工工序的持续时间，影响因素的不确定性使得工序持续时间存在不确定性。

在网络进度计划中，工序逻辑关系和活动时间一旦确定，施工关键路线和总工期也相应确定;当逻辑关系和活动时间发生任意变化，施工进度都可能会受到影响。传统的PERT网络是在逻辑关系确定的基础上，结合活动时间不确定性而建立的施工进度网络［8］。该网络未考虑逻辑关系不确定性对施工进度的影响，且得到的活动时间多为基于三时估计的特定β概率分布，难以满足实际施工中活动时间服从不同分布的要求。因此，为保证施工进度目标的实现，本文从工序间逻辑关系不确定性和活动时间不确定性两方面来改进经典PERT网络，用以开展输水隧洞施工进度风险分析，具体内容如图2所示。

输水隧洞施工工序繁多，制约关系复杂，工序间存在多种不同的逻辑关系。其中，基本逻辑关系有4种［9］，包括开始到开始(STS)、结束到结束(FTF)、开始到结束(STF)以及结束到开始(FTS)。混合逻辑关系是指相邻工作间既有STS、又有FTF的约束关系或者既有FTS、又有STF的约束关系。经典PERT网络未考虑逻辑关系不确定性对于施工进度的影响，而隧洞施工过程中风险事件的发生会导致风险处理活动这一新增工序的产生，使得原有进度计划逻辑关系发生变化。因此，需结合风险事件来分析逻辑关系变化对于施工进度的影响。

图2 基于改进PERT的输水隧洞施工进度风险体系

对于工序持续时间，满足在区间(a，b)内，活动时间概率密度函数连续且呈单峰形状，以及函数概率密度始终取有限正值条件的主要有β分布、正态分布和三角分布三种形式。β分布因其良好的偏态性，能根据所取参数的不同，实现对正态分布、均匀分布、三角分布等多种分布的逼近，因此工程中常采用β分布来描述网络活动时间的不确定性。在经典PERT网络中，活动时间往往通过三时估计值(最乐观时间、最可能时间和最悲观时间)确定，而该方法仅能得出三种特殊情况下的β分布函数，有一定缺陷。因此，本文在三时估计值的基础上增加四分位数c作为第四个参数，通过四参数估计得到各种不同的β分布形式，并利用舍选法对活动时间进行随机抽样。

二、输水隧洞施工进度风险分析方法

施工工序间的逻辑关系及工序持续时间对输水隧洞施工进度有重要影响。通过对改进PERT网络中的施工工序逻辑关系不确定性及活动时间不确定性分析来实现施工进度的风险分析，并运用Monte Carlo方法［10］，对改进的PERT网络进行求解。

1．逻辑关系不确定性分析方法

风险事件是逻辑关系不确定性的重要来源，具有两个主要特点:一是发生概率小于100%，即风险事件可能发生也可能不发生;二是一旦风险事件发生，采取的风险处理活动将作为新增工序插入原有进度计划中，使工序间逻辑关系发生变化，从而影响施工进度。针对上述两个特点，本文从定性和定量两个方面对风险事件进行研究，进而分析逻辑关系不确定性对于施工进度的影响。

(1)基于风险矩阵法的风险事件定性分析。风险事件的风险等级有高低之分。为提高风险分析效率，使得风险分析具有针对性，对高风险事件进行识别具有重要意义。风险矩阵法作为项目管理中常用的风险重要性识别方法，最早是由美国空军电子系统中心(Electronic Systems Center，ESC)采办小组于20世纪末提出的。该方法不直接依赖专家的主观意见，而是事先将风险概率和风险后果划分不同等级。在综合考虑风险概率和后果的条件下，将风险事件对项目的影响进行评估。

在风险事件分析中，将其按发生概率由高到低分为五个等级，分别为极可能发生、发生可能性很大、有可能发生、发生可能性很小以及极不可能发生。因风险事件发生引起逻辑关系变化对施工进度的影响程度同样可划分为五个等级，分别为关键、严重、中度、微小以及可忽略。各影响等级说明如表1所示。

综合考虑风险事件发生概率和发生后果的影响，运用风险评估矩阵法，将风险事件分为三个等级，分别为高风险事件(H)、中等风险事件(M)和低风险事件(L)。建立的风险评估矩阵如图3所示。根据风险评估结果，在进行隧洞施工进度风险分析时，可按风险事件等级的高低给予不同的关注度，对于高风险事件重点分析，而对低风险事件在条件有限的情况下甚至可以忽略，使得风险分析更有针对性。

表1 风险事件影响等级

(2)风险事件定量分析。在定性分析识别出高风险事件的基础上，进一步对风险事件发生概率及其影响后果进行定量分析。其中，风险事件发生概率是指隧洞施工中遇到涌水、断层、支护衬砌不合格、机械设备故障等情况，从而造成施工逻辑关系发生变化的可能性。由于同一类风险事件在不同工程中发生的概率具有较强的随机性，该参数可采用历史资料统计和专家打分相结合的方法来确定［7］。风险影响后果作为风险事件的另一个重要属性［11］，是指因风险事件发生导致的施工逻辑关系变化对施工进度造成的影响，可通过研究风险处理活动时间来体现。对于排水、打锚杆、固结灌浆、重新衬砌支护、机械故障排除等风险处理活动而言，其持续时间同样具有不确定性，活动时间分析方法与其他工序相同。

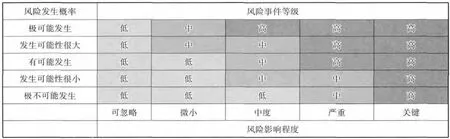
图3 风险评估矩阵

2．活动时间不确定性分析方法

活动时间不确定性分析主要包括活动时间分布的确定和活动时间随机抽样两方面。其中，合理确定活动时间分布是进行活动时间不确定性分析的前提;采用恰当的方法对已选时间分布进行随机抽样是进行活动时间不确定性分析的重要手段。

(1)活动时间分布的确定。活动时间分布包括正态分布、三角分布、β分布等多种类型。考虑β分布灵活性强，能对不同分布类型进行拟合的优点，工程中多采用β分布作为活动时间的分布类型。在本研究中，认为隧洞施工中各工序(包括风险处理活动)时间均服从β分布。经典PERT方法认为服从β分布的活动时间不确定性可通过期望μi和标准差σi来表现，且其均值和标准差可通过最乐观时间a、最可能时间m和最悲观时间b来计算

而实际β分布函数由最小值a、最大值b以及两个形状参数p，q共同决定，其概率密度函数为

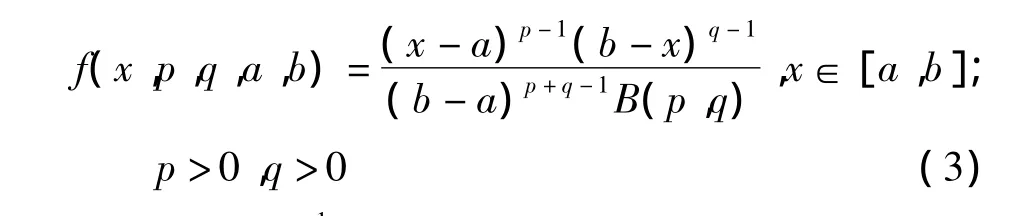
β分布的均值和标准差同样由4个参数决定

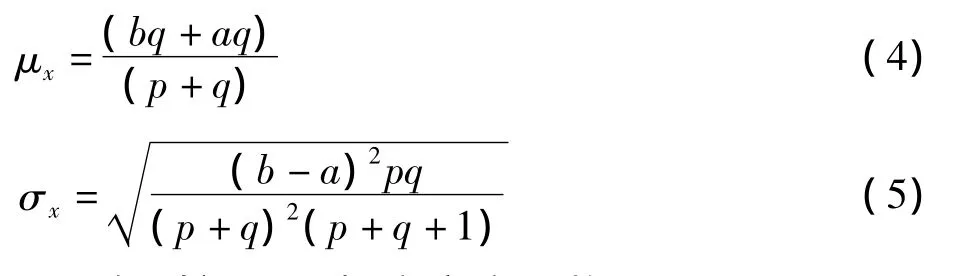
最可能时间m是概率密度函数 f(x，p，q，a，b)取最大时对应的 x值。a ＜m ＜b，可由等式 f'(x，p，q，a，b)=0求得

令式(1)=式(4)，式(2)=式(5)，并将式(6)带入，可得仅在三种特殊情况下，μi、σi才为 μx、σx的无偏估计，该三种特殊情况下的β分布曲线形式为

1)p=q=4:β曲线对称，m=(a+b)/2;

2)p=3+2，q=3-2:β曲线左倾，m=0．853 5b+0．146 5a;

由此可知，经典PERT中通过三时估计确定的β曲线只是β分布集合中的一部分，而实际

隧洞施工中各工序的活动时间可能服从各种不同的β分布形式。同时，由于β分布函数需由四个参数共同决定，仅由a、b、m三时估计值并不足以确定β分布形式。图4为相同三时估计值下的β曲线形式，虽然各曲线均满足a=2，m=4，b=8的三时估计条件，但其分布却各不相同。因此，为最终确定β分布，需在三时估计值的基础上增加新的参数。

图4 相同三时估计值下的β曲线分布形式

在β分布确定方面，Cliff Schexnayder等［12］提出β分布形式可由最乐观时间a、最悲观时间b以及下列任意一种组合来得到:1)均值和方差;2)均值和某一百分位数;3)最可能时间m和某一百分位数;4)任意两个百分位数。这些统计特征值将直接决定所得β分布形式，从而影响对活动时间的拟合效果。在统计特征值估计方面，Alpert等在关于概率评估员的培训进度报告中指出，直接用百分位数进行估计是最可靠、最不容易产生偏差的方法。Lichtenstein等［13］证实了采用百分位数进行估计的可行性，并指出采用四分位数，即0．25分位数、0．5分位数及0．75分位数进行估计能使结果的准确性进一步提高。基于上述研究，本文提出在原有三时估计值的基础上增加四分位数c作为第四个参数，用以确定β分布的具体形式。同时，在三时估计值确定的条件下，通过调整四分位数c的取值，可得到不同的β分布形式，克服了经典PERT中活动时间局限于三种特定β分布的不足。基于三时估计值和四分位数c的β分布函数四参数求解步骤如下:

1)在已知三时估计值和四分位数c的条件下，将a，b，m三时估计值带入式(6)，求解形状参数 p，q之间的关系

2)将a，b的值以及式(7)带入式(3)中，将β分布概率密度函数 f(x，p，q，a，b)转化成新的概率密度函数 F(x，q)。

3)对函数 F(x，q)在区间［a，c］上求积分，根据等式(8)即可求解形状参数q。

式中:当 c为0．25 分位数时，g 取 0．25;当 c为0．5 分位数时，g 取0．5;当 c为0．75 分位数时，g 取0．75。

4)将得到的q值代入式(7)，求解另一形状参数p，结合已知的a，b估计值，最终确定β分布的具体形式。

(2)活动时间随机抽样。在获得活动时间概率分布的基础上，还需进一步对所得分布进行抽样。对于形式简单的概率分布，可采用在［0，1］均匀分布上产生随机数，然后根据各活动时间服从的分布类型，对其累计函数求反函数的方法来得到相应的活动持续时间。而β分布形式复杂，难以准确从其密度函数上得到计算机抽样表达式，可通过舍选法进行活动时间抽样。舍选法通过建立随机数检验条件，利用这一条件舍选得到所需的随机数［14］。具体抽样步骤如下:

1)根据最乐观时间a，最可能时间m，最悲观时间b和四分位数c求得β分布函数和相应的参数。

2)对［0，1］区间均匀分布产生两个随机数 k1，k2。

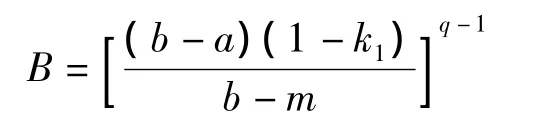
4)判断关系式AB＜k2是否成立，若成立，则x=a+(b-a)k1即为服从β分布的随机活动时间，若不成立，重复(2)～(4)直至满足条件。

(3)基于Monte Carlo仿真的改进PERT求解方法。为充分反映改进PERT网络中逻辑关系不确定性和活动时间不确定性对施工进度的影响，采用Monte Carlo仿真方法，在判断风险事件是否发生的条件下，对各工序持续时间(包括风险处理活动)进行随机抽样，求得关键路线和施工工期，并通过多次仿真进行施工进度风险分析。用Monte Carlo方法求解改进PERT网络的步骤如下:

1)根据隧洞实际施工方案，编制初始网络进度计划，估计原有工序及风险处理活动的最乐观时间a、最可能时间m、最悲观时间b以及四分位数c，并确定β分布的概率分布函数及相应的参数。

2)确定恰当的仿真次数N以及计划工期值。

3)判断各风险事件是否发生。在每一次仿真过程中，假定第i个风险事件的发生概率为Pi，对［0，1］区间产生均匀随机数ri，若ri＜Pi，则认为该风险事件发生，新增风险处理活动ei，调整原进度计划逻辑关系。

4)对各工序持续时间(包括风险处理活动时间)，根据其服从的概率分布函数进行随机抽样，然后按照CPM网络计算方法确定关键线路和隧洞施工工期，如此循环仿真N次。

5)对N次仿真结果进行统计分析，并获得计划工期完工概率、工期风险值、最关键线路以及工序关键度指标。

三、输水隧洞施工进度风险分析

隧洞施工进度风险反映了施工进度目标实现的不确定性。在进度风险分析中，完工概率、工期风险值、最关键线路以及工序关键度作为常用的风险评价指标，可为施工工期的论证以及线路、工序在统计意义上的重要程度分析提供依据。

1．完工概率及工期风险

要求隧洞施工计划工期T'的完工概率，即要求概率P(T≤T')的值。根据多次仿真所得仿真工期的统计特性值(包括均值、方差、最大值、最小值等)，运用概率统计方法，可得在同时考虑逻辑关系不确定性和活动时间不确定性条件下计划工期的完工概率。具体步骤如下:

1)设定分组组距Tg。令Tmin为N次仿真中施工工期的最小值，Tmax为N次仿真中施工工期的最大值，l为分组的组数，则组距Tg计算公式为

2)仿真结果分组。令 T1=Tmin+Tg，T2=T1+Tg，…，Tl=Tl-1+Tg，则相应的分组结果为

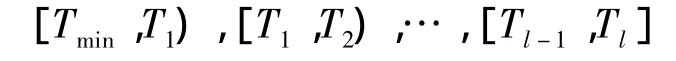
3)将N次仿真结果按区间统计频数，得到施工工期统计分布直方图和概率分布曲线。

4)对统计频数按区间累加，计算累计概率，得到总工期经验累积曲线即完工概率曲线。

输水隧洞施工计划工期T'的完工概率可通过经验累积曲线查出。

工期风险是指在规定时间内工程不能完工的概率，根据其与完工概率的关系，可得工期风险为

2．最关键线路和工序关键度

最关键线路是指在多次仿真中成为关键线路次数最多的线路。工序关键度是指在多次仿真中工序处于关键线路上的次数与仿真次数之比。通过多次施工仿真系统运行，在每次仿真结束后统计所得关键线路和关键工序，则可在多次仿真后确定最关键线路和工序关键度。

用工序关键度来表征关键线路的概率分布结果，对明确隧洞施工中的控制对象，把握关键线路、关键工序处理的优先原则具有重要的意义。同时，由于工序间逻辑关系不确定性和活动时间不确定性会造成隧洞施工关键线路的转移，对于关键度与最关键线路上工序关键度相差较小的工序也应给予足够的重视。

四、结 语

针对目前关于PERT网络的研究多未考虑工序逻辑关系对施工进度的影响，且活动时间仅局限于特定形式β分布的问题，本文从逻辑关系和活动时间两个方面对经典PERT进行了改进，以开展输水隧洞施工进度风险分析。首先，从风险事件的角度出发，将定性分析与定量分析相结合，探讨逻辑关系的变化对施工进度的影响;其次，在三时估计的基础上引入四分位数作为第四个参数，提出了不同β分布形式的确定方法;最后，采用Monte Carlo仿真方法对改进的PERT网络进行求解。本文所研究的基于改进PERT的输水隧洞施工进度风险分析方法对隧洞施工进度管理具有重要的理论意义和参考价值。

［1］胡连兴．复杂长距离引水隧洞群施工全过程仿真优化与进度控制关键技术研究［D］．天津:天津大学建筑工程学院，2012．

［2］Keeefr D L，Verdini W．Better estimation of PERT activity time parameters［J］．Management Science，1993，39(9):1086-1090．

［3］刘 武，杜志达，刘祥瞻．PERT网络活动时间参数估计的改进［J］．统计与决策，2008(4):150-153．

［4］JoséManuel Herrerı＇as-Velasco，Rafael Herrerı＇as-Pleguezuelo，Johan Renévan Dorp．Revisiting the PERT mean and variance［J］．European Journal of Operational Research，2011，210(2):448-451．

［5］蔡开玺，唐爱兵．提高水利工程PERT进度计划精度方法探讨［J］．吉林水利，2011(9):50-58．

［6］王 涛，蔡建峰．改进的PERT项目工期方差的估算方法［J］．工业工程与管理，2012，17(1):36-39．

［7］李明超，段志龙．耦合风险因素的大型地下厂房施工进度仿真分析［J］．水利水电科技进展，2014，34(5):39-44．

［8］王卓甫，丁继勇，刘 媛，等．基于Monte Carlo方法的PERT网络关键路线和最关键活动分析［J］．系统工程与电子技术，2012，34(8):1646-1651．

［9］王卓甫．工程进度风险计算研究［D］．南京:河海大学水利水电工程学院，2002．

［10］刘永强，邱云昌，姚悦铃．基于蒙特卡罗模拟仿真的工期估算［J］．工程管理学报，2014，28(5):88-92．

［11］张 静，付金强，张发瑜，等．水电工程投资风险分析及其应用研究［J］．天津大学学报:社会科学版，2008，10(3):228-233．

［12］Cliff Schexnayder，Kraig Knutson，Javier Fente．Describing a beta probability distribution function for construction simulation［J］．Journal of Construction Engineering and Management，2005，131(2):221-229．

［13］Lichtenstein S，Fischhoff B，Phillips L D．Calibration of probabilities:The state of the art to 1980［C］//Kahneman D，Tversky A．Judgement under Uncertainty:Heuristics and Biases．Cambridge:Cambridge University Press，1982:306-334．

［14］王丙参，魏艳华，孙永辉．利用舍选抽样法生成随机数［J］．重庆师范大学学报:自然科学版，2013，30(6):86-91．