基于优化欧氏距离的协同过滤推荐
2015-11-26陈小辉
陈小辉,高 燕
(榆林学院信息工程学院,陕西 榆林 719000)
0 引言
在过去的十余年中,网络上的信息数量呈爆炸模式大幅增长,同时也伴随着网上电子商务成交量的大幅提升,越来越多的人愿意通过互联网获取需要的商品和服务,可是由于网上巨大的信息量,用户获取有效信息的成本变得日益昂贵。推荐系统作为一种信息超载的有效解决方案逐渐在许多领域得到应用,特别是在一些电子商务网络中,如亚马逊、淘宝、京东商城等,运营商使用推荐系统帮助客户从海量的商品中挑选自己喜爱的书籍、CD、衣服、家具,甚至,汽车、房产等,而在一些社交网络和其他领域,也会用到推荐系统来帮助客户找到其潜在的朋友、客户等。
推荐系统所使用的算法主要有基于内容的推荐算法、协同过滤推荐算法和结合内容与协同过滤的推荐算法。协同过滤(Collaborative Filtering,CF)推荐是根据用户自身数据和对项目的评价数据,按照一定的邻居查找算法找出若干个相似性较高的邻居,使用这些邻居的评价数据预测当前用户对一些项目的评价并给出推荐[1-2]。协同过滤推荐算法又可进一步分为基于内存和基于模型2 类,前者常用于现在大多数的网上交易和服务系统,后者多用于相关的推荐算法研究。基于内存的协同过滤推荐过程是先计算用户或者item 之间的相似度,然后找相似度最高的若干邻居,再根据邻居的数据计算预测值并形成项目或者用户推荐[4]。
在现实网络推荐系统中,由于每个具体用户往往只是购买了或者使用了网站中数以万计商品或服务中的极少数一部分,因此用户仅仅对极少一部分项目有有效评价数据,这会导致用户项目评分数据矩阵异常稀疏从而产生数据稀疏问题;再次是冷启动问题,当协同过滤推荐系统中加入新的用户或者是新的评价项目时,新用户或项目的相关评价结果缺失或者是极为稀少,这些问题对于最近邻居的寻找以及有效推荐造成了一些困难[5-7]。
对于以上问题,许多研究人员都提出了一些改进的策略,文献[8]提出了一种分阶段评分预测法,该方法先采用聚类方法对原始评分矩阵中的用户和item 进行聚类,然后使用加权非负矩阵分解方法在聚类结果上进行预测推荐;文献[9]将融合聚类(Cluster Ensemble)算法应用到协同过滤推荐中;文献[10]使用奇异值分解技术实现对评分矩阵进行降维,从而寻找用户之间的隐含关系;文献[11]使用因子分析方法先对评价数据进行降维操作,然后用回归分析策略预测未知评价数据。以上解决方法在一些方面弥补了数据稀疏以及冷启动造成的困难,但是在进行用户或者项目相似性度量时,往往忽视用户向量之间(或项目向量之间)的长度差异,以及忽略共同评价项目的(或共同评价用户)数量上的不同,这往往会导致对于最近邻计算的失真。
本文提出一种采用优化欧氏距离的最近邻居度量算法,该算法考虑了评分空间中用户评分向量(或者项目评分向量)在数据维度上的差异,并且考虑了邻居和当前用户共同评分项目数以及每个用户的评分项目数。与通常采用的传统相似性计算方法比较,该算法的相似度计算结果更加符合实际情况,使推荐系统的推荐效率和准确率都有了明显改善。
1 相关工作
基于内存的推荐算法是目前商业推荐系统中应用最多的推荐算法,本文以其中基于用户(Userbased)的协同推荐系统为例来说明推荐系统的工作原理,该方法是在用户项目评价二维矩阵上,通过一定的方法寻找一些相似度较高的邻居,使用一定的算法按照邻居对待预测项目评分来预测当前用户对该项目的评分[12-13]。协同过滤推荐系统实现包括数据定义、相似度计算和评分预测及推荐。
1.1 评价数据定义
采集网络系统中所有用户对项目的评价数据形成一个二维矩阵,如图1 所示,该矩阵R 是一个n×m二维表,n 表示用户数量,m 表示评价项目数量,表中值Rx,y代表第x 个用户对于第y 个项目的评价结果。而评价结果,一般可分为显式评价和隐式评价2 类,显式评价是用户对项目的直接评分,隐式评价则是依据用户的一些行为如对相应网页的浏览频次、停留时间、是否购买等来给出的量化表示。矩阵的每一个水平向量表示一个用户对项目的评价,矩阵的每一个垂直向量表示某个项目从用户处得到的评价。用户评分矩阵如图1 所示。
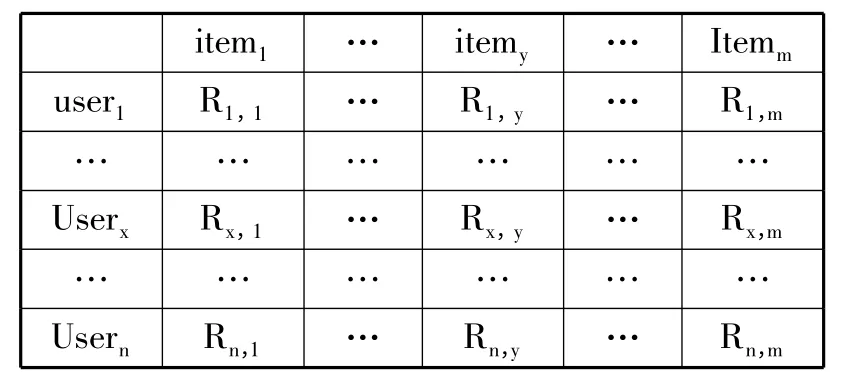
图1 用户-项目评价矩阵
1.2 相似度计算
协同过滤推荐算法的根本在于对最近邻居的查找,查找中用以度量用户相似性的传统方法有向量空间相似性度量方法(VSS,Vector Space Similitude)以及皮尔森相似性度量方法(PCC,Pearson Correlation Coefficient)2 种。向量空间度量方法是把用户对n 个项目的评价值作为一个n 维向量,2 个用户之间的相似值使用2 个n 维向量之间的夹角余弦值来表示[14]。假设用户u 和用户v 对于产品i 的评分分别为rui和rvi,用户u 和v 所共同评价过的产品集合为Iuv;则用户u 和v 的相似度计算如式(1)所示。
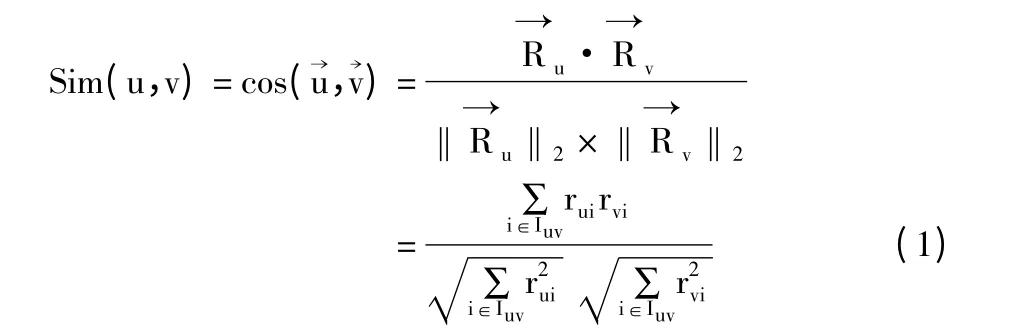
PCC 相似性度量算法则是基于变量的线性关系,用户u,v 的相似度计算Sim(u,v)如式(2)所示,分别表示u 和v 所有有效评价的平均值,Iuv表示被用户u 与用户v 共同评价过的项目集。

1.3 预测评分与项目推荐
在使用VSS 或者PCC 相似性度量算法计算得到两两用户间的相似度后,得到K 个与当前用户具有最大相似度的邻居,如果需要对当前用户的某项未评分项目进行预测时,可以使用特定的计算方法基于邻居在该项目的评价来得到预测值[15]。用户u 对项目i 的预测评分值可以使用公式(3)计算,为提高算法的可靠性,式中考虑了用户间评分习惯和评分尺度的不同,并且还使用了用户所有评价的平均值,N(u)为找到的相似邻居集合,集合规模为K。计算得到项目的预测评分后,可对未评价项目排序,并形成若干推荐项目。
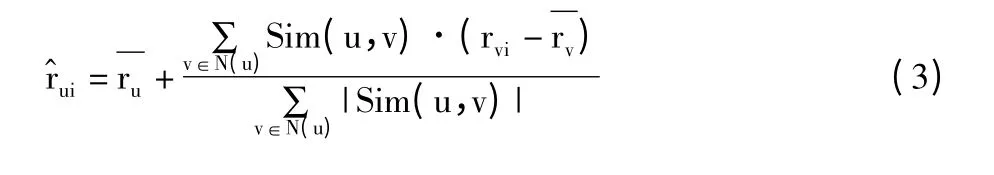
2 基于优化欧氏距离邻居相似性度量方法
2.1 传统协同过滤推荐算法的缺陷
在传统的协同过滤推荐系统中对于用户之间相似度的计算方法,无论是VSS 算法还是PCC 算法都是在用户对项目的原始评价值上计算相似性,而没有考虑用户的评价数值大小差异和评价项目数量的差异,这样常常会得到与实际情况不相符合的推荐结果[16-17]。例如图2 表示5 个用户对5 个项目的评价矩阵,用户的评价值在1 和6 之间,空白项目表示用户未做评价。假设要预测用户u2对于项目i5的评价,依次使用VSS 和PCC 邻居相似性度量算法计算用户相似度,可得u1和u2的相似值为0.9448 和0.6703,u2和u3的相似度为0.8451 和0.5273,从计算结果看u1与u2的相似性要比u2与u3的相似性强。但是用户u1的评价值位于[1,6]区间,而用户u2和u3的评价值位于[1,4]区间,从习惯性常识来看u2与u3的相似性应该更强,在预测用户u2对项目i5的评价时更应当考虑的邻居是u3并不是u1。这是因为VSS 算法和PCC算法都不考虑不同用户在对项目评分时评价值的范围差异和有效评分项目数的差异。

图2 用户项目评分矩阵示例
2.2 距离邻居相似性度量方法
针对传统邻居相似性度量方法的缺陷,本文设计了一种基于优化欧氏距离的相似性度量方法(Optimization Euclidean Distance Similarity Measurement,简记为OED)。传统的欧氏距离方法也可以用来计算用户向量之间的距离,但是推荐系统中用户向量的欧氏距离一般是在不同维度的向量空间中计算,直接用它们的欧氏距离度量相似度和传统的用户相似性度量方法结果差异不大,而本文所提出的OED 方法在度量2 个向量的相似性时考虑了不同用户向量所处的多维向量空间的维数差异。
假设在m 维向量空间中用户u 和用户v 的评价向量分别为,distmax表示m 维空间上的最大欧氏距离,dist()表示用户向量之间的欧氏距离,则用户u 和用户v 之间的归一化欧氏距离如式(4)所示。

用户u 和用户v 的相似程度可以用式(4)的倒数来表示,用Iuv代表用户u 与用户v 共同评分项目的集合,用户评价向量的维度为m,且所有用户的最大评价值为rmax,最小评价值为rmin,则用户u,v 的相似度计算Sim(u,v)如式5 所示。
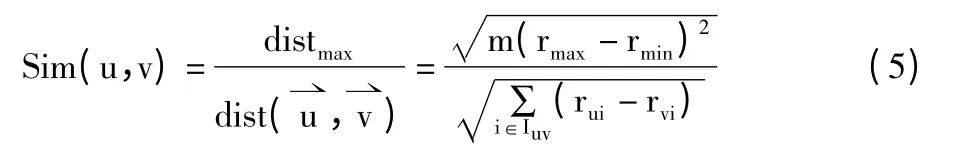
考虑不同用户有效评价项目的数量差异以及共同评价项目的数量差异,为了使相似度值更符合实际情况,在公式(5)归一化处理的基础上引入杰卡德相似系数,则得到公式(6),式中Iu和Iv分别表示用户u和用户v 的有效评价项目集合,|Iuv|、|Iu∪Iv|表示相应集合中的项目个数。
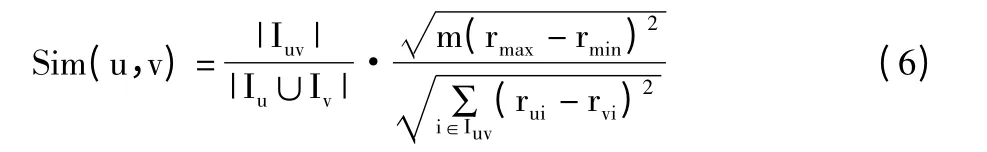
公式(5)、(6)都假设不存在2 个用户u,v 对所有项目的评分完全相同,此时用户u 和v 的相似度越高,则Sim(u,v)值越大;如果存在u,v 对所有项目的评分完全相同,则默认这2 个用户的相似值取最大值。
3 实 验
3.1 数据集
为了比对测试OED 相似性度量方法的效果,采用来自于Group Lens 研究小组提供的Movielens 电影评价数据集。该数据集包含有943 个用户对于1682部电影的评价,所有用户都有20 个以上的评价值,数据集的稀疏度为93.7%。由于实际评价数据往往较为稀疏,实验中对原始数据进行随机删减,形成了稀疏度分别为2%、4%、6%、8%、10%、12%、14%、16%、18%和20%的10 个稀疏评价矩阵。
3.2 评价标准
实验中使用常用的评价推荐是用准确度的平均绝对误差(Mean Absolute Error,MAE)值来评价OED算法的效果,MAE 值是预测值和实际值之间的方差均值,如式(8)所示。用户u 对项目i 的真实评价用rui表示,通过算法预测的用户u 对项目i 的评分值用表示,N 为全部预测评价值数量,MAE 值和预测的准确度成反比,值越小则预测得越准确。
3.3 实验方案
为了检验OED 相似性度量方法的有效性,实验中采用了基本欧氏距离相似性度量算法(ED,Euclidean Distance)、向量空间相似性度量算法VSS、优化的向量空间夹角余弦算法AdjCOS 和皮尔森相似性度量算法PCC。传统欧氏距离相似度计算公式见公式(7),VSS 和PCC 相似度计算公式见公式(1)、公式(2),ED 和AdjCOS 度量方法见公式(7)、公式(8),式中rmid为用户评分空间中最大评价值与最小评价值的平均数。依次将5 种相似度计算算法用到基于用户的协同过滤推荐中去,采用公式(3)来计算预测值。
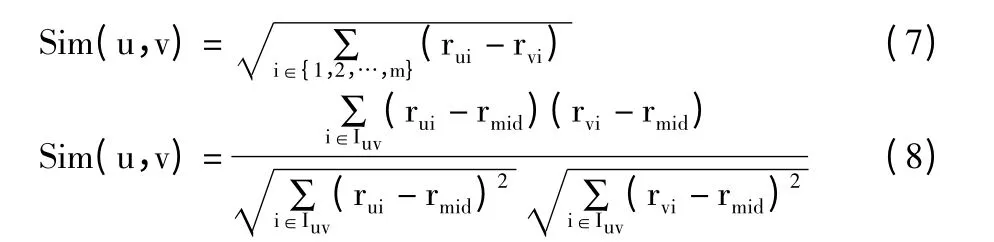
采用五折交叉验证(5-Fold Cross Validation)来实验,分别从10 个稀疏评价矩阵中随机抽取10%的数据作为测试数据集,剩余部分为训练数据集。共进行5 次划分,在每一折实验中,基于训练集数据预测测试集数据,并通过比较预测评分和真实评分得出每一折的MAE 值,最后计算得到平均MAE 值。实验中最近邻居数k 分别取10、20、30、40 和50,图2 和图3 分别给出了邻居数k 等于10 和50 时相似度度量方法的性能比对。
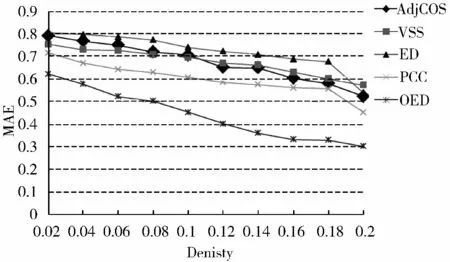
图2 k=10 时性能比对图
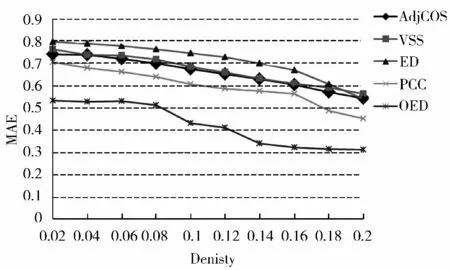
图3 k=50 时性能比对图
从图2 和图3 可以看出,采用OED 方法推荐系统的MAE 值要明显小于采用原始欧氏距离相似性度量方法的推荐系统,而且也小于应用其他3 种传统的相似性度量算法的推荐系统,说明使用OED 算法其推荐结果更加接近于实际情况。并且从图(2)和图(3)中可以看出当评分矩阵的数据密度逐渐增大时OED 推荐算法的MAE 值变化不大,但是当用户评分矩阵数据较为稀疏时候,OED 的表现更优秀,说明当数据稀疏,用户向量的维度趋于多样,这时OED 算法有更优秀表现。
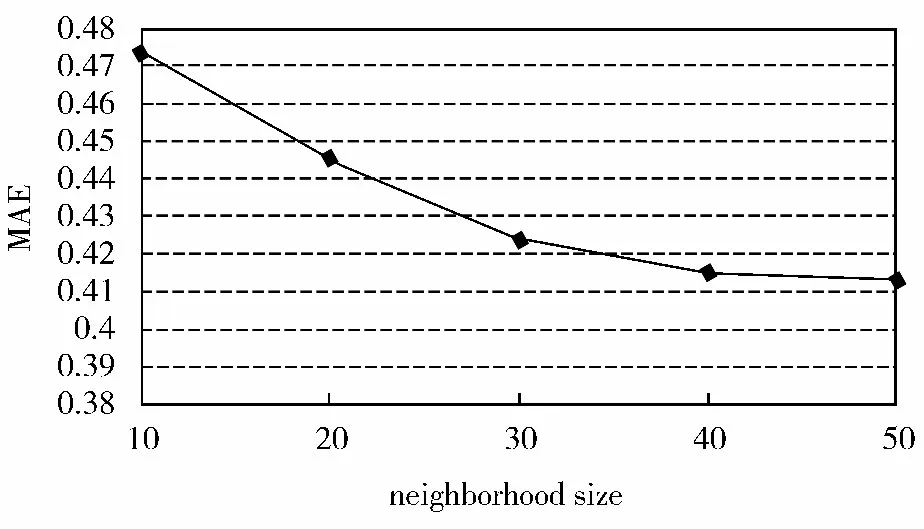
图4 邻居数对MAE 值的影响
图4 为评分矩阵数据密度取10%时,邻居数从10 变化到50 对应的OED 算法推荐MAE 值的变化,说明OED 算法推荐性能会随着邻居数的增长而提高,当邻居数增长至40 以后,MAE 值变化趋于平缓。实验表明相对于其它传统推荐算法,使用OED 邻居相似性度量算法能够有效提高过滤推荐系统的性能,而且该方法能够应用于数据稀疏度较高的评价矩阵。
4 结束语
系统过滤推荐系统中所采用的传统相似性度量方法往往存在一定的不足,本文所提出的基于归一化欧氏距离邻居相似性度量方法,可用于解决各协同过滤推荐系统中的对评价项目的评分预测和推荐问题,特别是对于实际应用推荐系统中高度稀疏的评价数据,该算法能够更加准确地查找邻居,从而提高推荐的性能。
[1]邓晓懿,金淳,韩庆平,等.基于情境聚类和用户评级的协同过滤推荐模型[J].系统工程理论与实践,2013,33(11):2945-2953.
[2]Shi Y,Larson M,Hanjalic A.Exploiting user similarity based on rated-item pools for improved user-based collaborative filtering[C]// Proceedings of the 2009 ACM Conference on Recommender Systems.2009:125-132.
[3]Robert B,Yehuda K,Chris V.Modeling relationships at multiple scales to improve accuracy of large recommender systems[C]// Proceeding of the 13th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.California,USA,2007:95-104.
[4]代金龙.协同过滤算法中数据稀疏性问题研究[D].重庆:重庆大学,2013.
[5]王道平,李秀雅,杨岑.基于内容相似度的知识协同过滤推送算法研究[J].情报理论与实践,2013,36(10):86-90.
[6]王玉斌,孟祥武,胡勋.一种基于信息老化的协同过滤推荐算法[J].电子与信息学报,2013,35(10):2391-2396.
[7]吴湖,王永吉,王哲,等.两阶段联合聚类协同过滤算法[J].软件学报,2011,21(5):1042-1054.
[8]Tsai C F,Hung C.Cluster ensembles in collaborative filtering recommendation[J].Applied Soft Computing,2012,12(4):1417-1425.
[9]Sarwar B,Karypis G,Konstan J.Item-based collaborative filtering recommendation algorithms[C]// Proceedings of the 10th International World Wide Web Conference.New York,2001:285-295.
[10]赵宏霞,王新海,杨皎平.基于用户和项目因子分析的混合协同推荐算法[J].计算机应用,2011,31(5):1382-1386.
[11]李忠俊,周启海,帅青红.一种基于内容和协同过滤同构化整合的推荐系统模型[J].计算机科学,2009,36(12):142-145.
[12]李涛,王建东,叶飞跃,等.一种基于用户聚类的协同过滤推荐算法[J].系统工程与电子技术,2007,29(7):1178-1182.
[13]刘庆鹏,陈明锐.优化稀疏数据集提高协同过滤推荐系统质量的方法[J].计算机应用,2012,32(4):1082-1085.
[14]李改,潘嵘,李章凤,等.基于大数据集的协同过滤算法的并行化研究[J].计算机工程与设计,2012,33(6):2437-2441.
[15]李华,张宇,孙俊华.基于用户模糊聚类的协同过滤推荐研究[J].计算机科学,2012,39(12):83-86.
[16]于洪,李转运.基于遗忘曲线的协同过滤推荐算法[J].南京大学学报(自然科学版),2010,46(5):520-527.
[17]王海艳,张大印.一种可信的基于协同过滤的服务选择模型[J].电子与信息学报,2013,35(2):349-354.
