基于AUC 的非参数快速变点检测算法

吴学龙，徐维超

(广东工业大学自动化学院，广东 广州 510006)

0 引言

目前，变点检测技术已经广泛应用到工业质量控制、气候模拟、网络安全、欺诈检测等各个领域，具有十分重要的研究意义。

变点(也称异常点或孤立点)，即模型中某个或某些量起突然变化的点，这种变化往往反映事物的某种质的变化［11］。例如，在工业生产过程中，电机转速在某一时刻可能由于故障而突然变大或变小;在网络监测过程中，服务器接收的数据包可能因为分布式拒绝服务攻击(DDos)而突然激增。因而，及时准确地检测出变点，并采取进一步处理就显得很重要。

常见的变点检测方法根据过程的分布情况可以分为参数方法和非参数方法。文献［4］中所提出的累积和控制图(CUSUM)是一种常用的参数方法，而文献［10］提出了一种改进的非参量的CUSUM 算法，并将其应用到网络安全监测中。在实际生产环境的检测过程中，过程的分布或者参数往往是未知的，应用参数方法检测变点，模型太清晰以至于在很多应用场合中并不灵活。又由于历史数据不足、采样误差、噪声等不确定因素的影响，直接通过历史数据来估计过程的参数往往也十分困难。

为了解决上述参数方法的不足，本文提出一种新的非参数检测方法，从模式识别的角度出发，首次将2 类AUC(Area under the Curve，曲线下面积)应用到变点检测中。AUC 本质上表征的是2 个随机变量X和Y 的统计关系，常用来分析模式识别中的二分类问题:

将变点检测看成一个二分类问题:在变点发生的前后的时间段中，把变点前的样本看成一个随机变量，变点后的样本看成另一个随机变量，利用AUC 作为统计量，采用在文献［1］中提出的基于秩统计量的快速算法对变点进行快速检测。

1 相关技术

1.1 CUSUM 算法简介

Page［4］于1954 年提出CUSUM 控制图，它常被用于解决检测过程中的小偏移问题。该算法可以用假设检验的形式描述，假设已经抽取了m 个观测值，则:

利用序贯概率比检验理论，序贯概率比为:

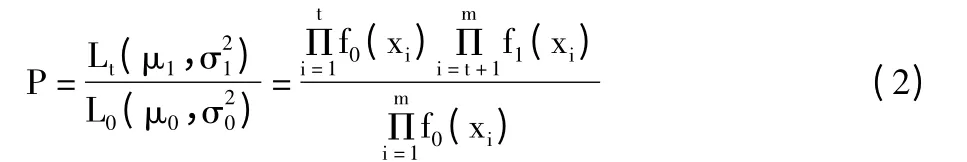
其中，f0(·)为N(μ0，)的密度函数，f1(·)为N(μ1，)的密度函数。

确定常数A 和B，使得:

若P≥A，则相应的备择假设Ht成立，过程失控;

若P ≤B，则原假设H0成立，过程受控;

若B ＜P ＜A，则不能给出定论，待抽取下一观测值，重复进行以上检验。

通常A 通过以下方法确定:令α 表示第一类错误的概率，β 表示第二类错误的概率，取A=(1 -β)/α［13］。

常规的CUSUM 控制图往往假设过程数据服从正态分布的基础上，当过程参数未知时，CUSUM 控制图往往假定过程初始处于受控状态，并持续足够长时间，但在实际操作中，上述假定并不一定都能满足。

1.2 AUC 简介

接收机工作特性(Receiver Operating Characteristics，ROC)分析是发端于20 世纪40 年代的一种统计分析方法，主要用于评估二战期间雷达接收机的性能。由于统计特性优越，数学意义清晰，ROC 分析方法目前已经广泛应用于电子工程、生物、医学、金融以及模式识别等各学科。

接收机工作特性是由在不同判决门限下虚警概率和发现概率所构成的一条曲线来描述的(如图1 所示)。

图1 接收机工作特性曲线示意图

在用AUC 分析2 分类问题时，AUC 的取值(这里用θ 表示)与分离度有关(如图2 所示):

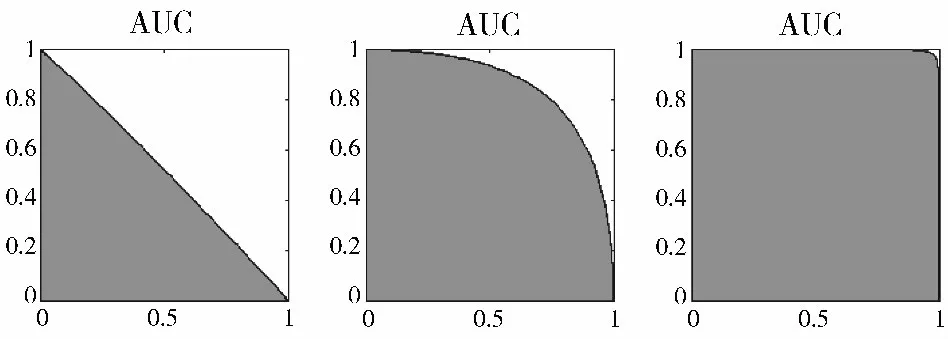
图2 AUC 曲线示意图

已经证明，该AUC 与统计学中著名的曼-惠特尼U 统计量等效。在连续概率分布假设下，当样本长度足够大时，AUC 依概率趋于一个高斯分布，其均值和方差可以表示为母体累计概率密度函数的无穷积分形式。

在文献［1］中推导了当母体为均匀分布、高斯分布、高斯混合分布、拉普拉斯分布、柯西分布及瑞利分布下，AUC 的均值与方差的解析表达式，并提出一种新的基于秩统计量的快速算法，将算法的时间复杂度从三次方量级降低到线性对数量级(Nlog (N))，为AUC 的理论研究与算法实现做出了新的贡献，而本文所做的主要工作也正是在此基础上展开。

2 基于AUC 的变点检测

2.1 第一阶段

第一阶段，常常也称为预分析阶段。实际生产环境中，在大多数情况下过程均值和方差都是未知的，通常的做法是在样本可控状态下估计参数，然后根据估计建立控制图。与常规非参数方法不同，本文在预分析阶段并不是直接采取估计过程的均值和方差，而是通过先计算样本数据的AUC(见式(3))值，然后再根据AUC 估计均值和方差。

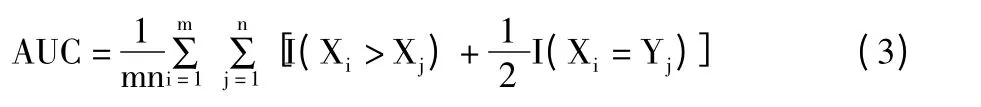
其中，X ＞Y，I(·)=0;X ＜Y，I(·)=1。

具体来讲，本文采用的是对原始样本数据进行加窗处理的方法(如图3 所示):选取2 个连续的窗口X和Y(假设窗口大小分别为m 和n，大小固定)，通过逐步滑动窗口来对原始数据进行处理。

图3 AUC 用于突变点检测示意图

从图3 中可以观察到，由于变点的出现，使得样本数据可以人为划分为2 类:即突变前和突变后。样本数据经预处理后，存在一个很明显的尖峰(AUC 取局部最大值)。从分类角度来讲，在这个点类分布最优，而这个点很明显就是要检测的变点。经文献［1］证明，样本数据经处理后将服从如下分布:

2.2 第二阶段

在得到了过程所服从的分布参数后，可以通过假设检验的方法来进行变点检测。与常规CUSUM 算法相比，本文也是通过设定一个门限来判断是否有变点产生。这里主要讨论2 个因素对检测结果的准确性的影响，即偏移程度(Δ)和窗口大小(m)。

图4 所示为样本数据容量为1 000，含有一个变点，进行5 000 次模拟实验所得。从图中可以观察到，随着偏移程度(Δ)的增大，检测的准确性也随之增大。

图4 偏移程度(Δ)对检测准确性的影响

图5 为测试改变窗口大小对检测结果的影响。从图中可以观察到，随着窗口大小的增加，检测结果的准确性也会在一定范围有所提高。由式(4)可以得知，其方差σ2随着窗口大小(m)的增加而减小。但窗口的增大会影响检测的实时性，这也是实际生产环境中需要考虑的一个重要因素，因而m 和n 到底取多大才合适，则需要根据实际情况而定。

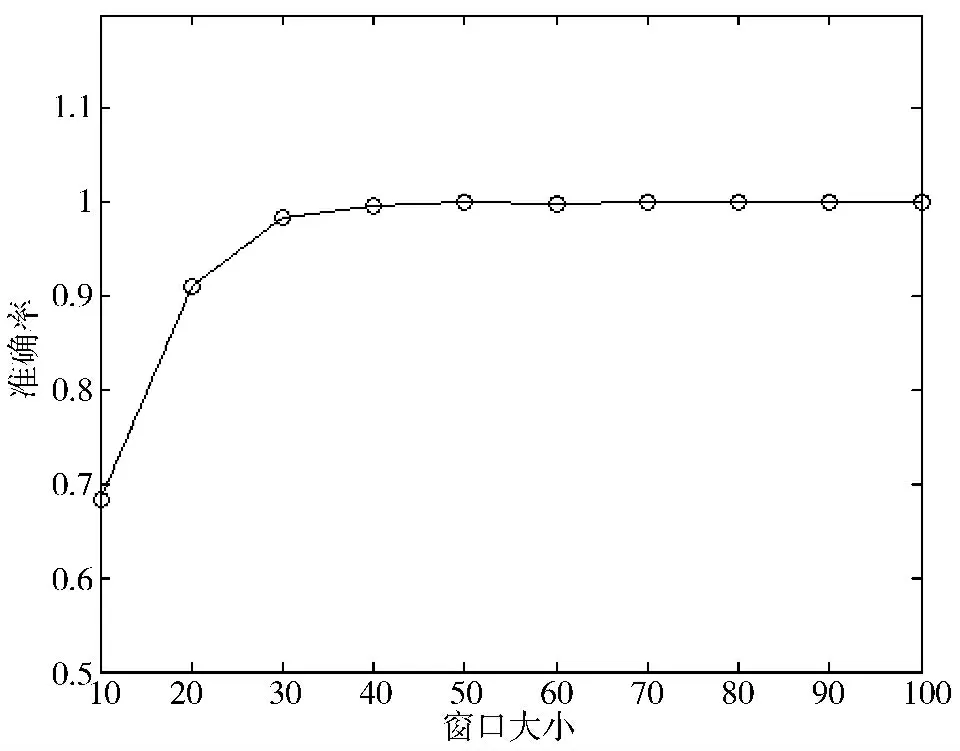
图5 窗口大小对检测结果的影响

3 实验结果与分析

为了进一步验证本文提出的检验方法的有效性，在观测数据服从不同分布的情况下，笔者将常规CUSUM 算法与本文所提方法进行对比。选取样本容量为1 000，突变发生在样本区间［500，1000］，通过调节参数，使得2 种方法的虚警率(α)同为5%，图6 为5 000 次模拟仿真的结果。

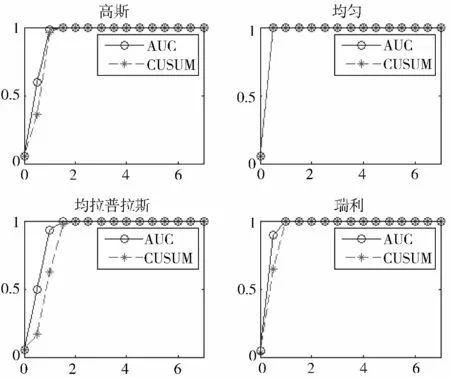
图6 基于CUSUM 算法与基于AUC 的算法检测结果示意图

通过图6 可以发现，当样本数据来自未知分布时，与常规的CUSUM 算法相比，本文所提的方法在准确性以及稳健性方面要优于CUSUM 算法。

4 基于AUC 的多变点检测

目前常见的变点检测方法多用于检测单个变点，对检测样本数据中多个变点的情况存在不足，检测的效果并不理想。所以，笔者尝试将本文所提出的方法初步应用到多个变点的环境中。

图7 多变点环境下检测示意图

从图7 中可以看出，当2 次连续跳变的间隔满足一定的条件时，采用本方法检测多变点与单变点的情形十分类似。

5 结束语

本文针对目前变点检测技术中参数方法存在的一些不足，提出了一种新的非参数方法。通过互联网检索发现，本文应为首次将AUC 应用到变点检测中，并在多种过程分布下进行了测试，根据实验结果显示，本方法可以取得比常规CUSUM 算法更好的稳健性，而且在解决多变点检测方面也有比较理想的效果。但本文的方法同样存在一些不足，在窗口的大小选取方面往往需要根据经验和实际情况确定，当为了满足实时性而使得窗口取值过小时，往往会使虚警率偏高，是否可以通过进一步处理AUC 数据来进行优化尚需要进一步研究。

［1］Xu Weichao，Dai Jisheng，Hung Y S，et al.Estimating the area under a receiver operating characteristic(ROC)curve:Parametric and nonparametric ways［J］.Signal Processing，2013，93(11):3111-3123.

［2］Xu Weichao，Tse H F，Chan F H Y，et al.New Bayesian discriminator for detection of atrial tachyarrhythmias［J］.Circulation，2002，105(12):1472-1479.

［3］Huang Jin，Ling C X.Using AUC and accuracy in evaluating learning algorithms［J］.IEEE Transactions on Knowlege and Data Engineering，2005，17(3):299-310.

［4］Page E S.Continuous inspection schemes［J］.Biometrika，1954，41(1-2):100-115.

［5］Basseville M，Nikiforov I V.Detection of Abrupt Changes:Theory and Application［M］.Englewood Cliffs:Prentice Hall，1993.

［6］Brodsky B，Darkhovsky B.Sequential change-point detection for mixing random sequences under composite hypotheses［J］.Statistical Inference for Stochastic Processes，2008，11(1):35-54.

［7］Kühn C.An estimator of the number of change points based on a weak invariance principle［J］.Statistics and Probability Letters，2001，51(2):189-196.

［8］Yang Su-fen，Cheng Smiley W.A new non-parametric CUSUM mean chart［J］.Quality and Reliability Engineering International，2011，27(7):867-875.

［9］Qiu Peihua，Hawkins D.A rank-based multivariate CUSUM procedure［J］.Technometrics，2001，43(2):120-132.

［10］于明，陈卫东，周希元.一种自适应非参量CUSUM 控制图算法［J］.计算机科学，2008，35(7):25-28.

［11］陈希孺.变点统计分析简介［J］.数理统计与管理，1991，10(2):52-59.

［12］濮晓龙.关于累积和(CUSUM)检验的改进［J］.应用数学学报，2003，26(2):225-241.

［13］涂玉娟，冯士雍.几类正态过程的CUSUM 图［J］.应用概率统计，2008，24(2):135-147.

［14］Saghir A.统计过程监控中灵活而稳健的控制图［D］.杭州:浙江大学，2014.

［15］秦瑞兵，田铮，陈占寿.独立随机序列均值多变点的非参数检测［J］.应用概率统计，2013，29(5):449-457.

［16］张学新.变点检测问题最新进展综述［J］.江汉大学学报(自然科学版)，2012，40(2):18-24.