Stability of Semi-implicit Finite Volume Scheme for Level Set Like Equation
2015-11-26KIMKwANGILANDSONYONGCHOL
KIM KwANG-ILAND SON YONG-CHOL
(1.School of Mathematics,Jilin University,Changchun,130012)
(2.Department of Mathematics,University of Science,Pyongyang,D.P.R.Korea)
Communicated by Ma Fu-ming
Stability of Semi-implicit Finite Volume Scheme for Level Set Like Equation
KIM KwANG-IL1,2AND SON YONG-CHOL2
(1.School of Mathematics,Jilin University,Changchun,130012)
(2.Department of Mathematics,University of Science,Pyongyang,D.P.R.Korea)
Communicated by Ma Fu-ming
We study numerical methods for level set like equations arising in image processing and curve evolution problems.Semi-implicit finite volume-element type schemes are constructed for the general level set like equation(image selective smoothing model)given by Alvarezet al.(Alvarez L,Lions P L,Morel J M.Image selective smoothing and edge detection by nonlinear diffusion II.SIAM J.Numer. Anal.,1992,29:845–866).Through the reasonable semi-implicit discretization in time and co-volume method for space approximation,we give finite volume schemes, unconditionally stable in L∞and W1,2(W1,1)sense in isotropic(anisotropic)diffusion domain.
level set like equation,semi-implicit,finite volume scheme,stability
1 Introduction
Level set like nonlinear parabolic equations arise in a wide range of applications as image processing and computer vision,phase transition,crystal growth,flame propagation,etc., and they are mainly related to the curve and surface evolution such as mean curvature motion of level set.In this paper,we study numerical methods for solving the following general level set like equation(image selective smoothing model combining isotropic and anisotropic diffusion)given by Alvarez et al.[1]:


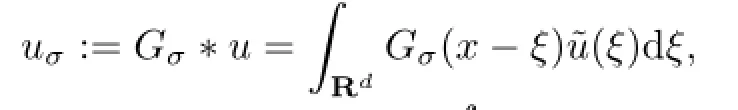

The equation is accompanied with zero Dirichlet(or Neumann)boundary and initial conditions as follows:

where ν is the unit normal to the boundary of Ω.We assume that the initial function

In image processing(smoothing or de-noising),the initial function u0(x)represents the grey level intensity of the processed image and the solution u(t,x)is the scaled(filtered, smoothed)version of u0(x)according to time-scale t.
In the special case of g,f≡1,(1.1)reduces to the well-known mean curvature flow level set equation,which has attracted a lot of attention with wide applicability to the geometrical problems such as curve and surface evolution[2–4].Concerning image processing,the mean curvature equation satisfies the so-called morphological principle on invariance of image analysis to contrast changes and then the process of nonlinear filtration is understood as image multi-scale analysis[5].
The level set like equations have been successively introduced to image processing(image restoration and segmentation)in the last years[1–2,5].In image filtration,it is generally desirable to smooth the homogeneous regions of the image with the purpose of noise elimination and image interpretation and on the other side,to keep the accurate location of boundaries,i.e.,edges.Therefore,it seems natural to modify the diffusion operator so that it diffuses more in direction parallel to the edge and less in the perpendicular one.From such consideration in[1],the authors proposed the image selective smoothing model with preserving edge positions:

This model is further improved(see(1.1))from the fact that it is not necessary to diffuse anisotropically at the points,where gradient is low and moreover to preserve the edges without contrast.
The level set like equations have been extensively studied theoretically[3–4]and numerically[6–16].Especially our numerical method is related to the complementary volume(also called co-volume or finite volume element)methods in implicit[16]and semi-implicit[8–15] forms in time.However,one could also notice important differences between combinative model(1.1)and other level set like models(see,e.g.,(1.5)and other literatures[8–13]).
In Section 2,we construct the finite volume-element scheme for(1.1)by using a sort of semi-implicit discretization in time and co-volume method for space approximation,which is linear and has a unique solution.In Section 3,we give existence of generalized solution for the proposed scheme through L∞-estimate on discrete solutions and stability results on decrease of L2,L1-norm of gradients(total variation)in isotropic and anisotropic diffusion domains,respectively,in subsequent discrete time steps.
2 Semi-implicit Finite Volume-element Scheme
In order to discretize(1.1),we first give a sort of semi-implicit discretization in time and then fully discrete co-volume scheme.For given an N∈N,we set a uniform discrete timescale step τ=T/N.First of all,we separate the isotropic diffusion term from anisotropic diffusion one with the purpose of constructing the discrete analogue of continuous model, which can clearly reflect isotropic and anisotropic characteristics.Then we replace timescale derivative by backward difference and the nonlinear parts in every diffusion term are treated from the previous time step while the linear ones are considered on the current time level.This leads to the following semi-implicit discretization in time-scale.
For n=1,···,N,

Now we turn to the full discretization of(2.1)and(2.2),based on finite volume methodology.Here we only consider the case of 2D space.
In image processing,a discrete image is given on a rectangular structure of pixels and values of the discrete image intensity are considered as approximations of continuous image intensity function in centers of pixels.Then one usually uses a finite volume mesh,which is given by a family of control volumes(co-volumes)corresponding to the pixel structure of the image.The centers of co-volumes(pixels)is called degree of freedom(DF)nodes. Together with the primary mesh,the dual mesh is also used,which is composed of dual control volumes which are rectangular parts given by connecting neighboring DF nodes.For our finite volume-element scheme,we use a triangulation coincided with the pixel structureof the image,which is obtained by splitting every dual control volumes into two triangles (see Fig.2.1).We denote the triangulation by Th.The computational domain Ω is then the union of these triangles,i.e.,the image domain minus outer half of every boundary pixel.

Fig.2.1 Solid line rectangles:co-volumes corresponding to image pixels, dashed lines:the triangulation for the finite volume-element method, round points:degree of freedom(DF)nodes.
Note that there exists a one-to-one correspondence between co-volumes and DF nodes. Then every co-volume Viis associated with the DF node i(i=1,···,M)of the triangulation Th.For each DF node i,N(i)denotes the set of all DF nodes j(neighboring nodes)connected to the node i by the dual mesh.The line segment(edge of dual co-volume)connecting i and j is denoted by σijand its length by hij.Then every co-volume Viis bounded by line segments(co-ed
ges)eijof the length lijthat are perpendicular to the line segment(dual co-edge)σij,j∈N(i).We denote bythe set of simplices having σijas an edge.We define the set Vhof continuous piecewise linear functions on the triangulation Thas follows:

Then|∇uh|,uh∈Vhhas a constant value on every simplex T∈Th.We denote it by |∇uT|.For any uh∈Vh,we denote by ui,the approximate value uh(xi)at the node i of the triangulation Th.Let u0=Ih(u0)∈Vh(Th)be the nodal interpolant of u0.Niis the set of simplices that have the DF node i as a vertex.
Considering the average value of gradients in co-volume,we define
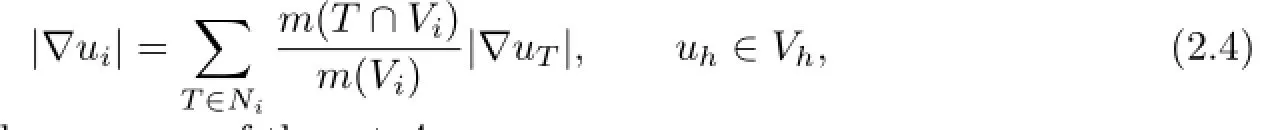
where m(Λ)denotes the measure of the set Λ.
For any fixed α∈R,the following function is used.
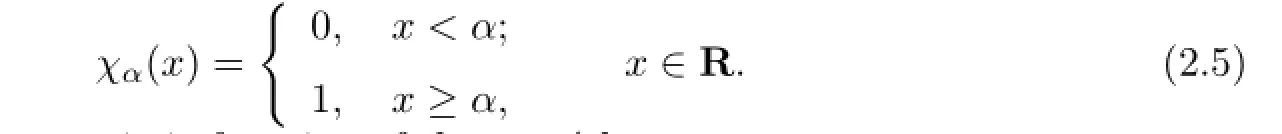
We also denote the characteristic function of the set A by χA.
Now transforming two equalities(2.1),(2.2)a little and integrating them over a covolume Vi,i=1,···,M,respectively,we get the following integral expressions:

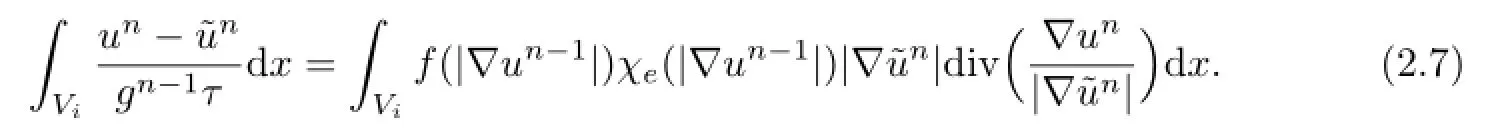
In the above we note that it holds

due to properties of convolution(see,e.g.,[8,14]).
We approximate the left hand sides of(2.6)and(2.7),respectively,as follows:


The discrete approximation ofthus the functionis obtained by using the numerical method applied to(2.1)with g,f≡1 in the below.Using divergence theorem, for the right hand side of(2.6),we obtain

When being approximated by piecewise linear function,the first term in the above becomes zero and the second term is approximated as follows.

Similar to the above,for the right hand side of(2.7)we get

In the case of uniform mesh with edge size h,m(Vi)=h2and hij=lij=h.
On the one hand,since the denominators of(2.2)(and therefore(2.11))can vanish,we regularize in the sense of Evans and Spruck[4].We use the following denotations related to the regularization.For ϵ,δ>0,

and

For every fixed real number α∈(0,1),we define

Then we define the coefficients as follows.For fixed ϵ,δ>0,

The boundary condition(1.2)is naturally approximated at the boundary points.
The linear semi-implicit finite volume-element scheme for(1.1)–(1.3)is as follows.

We denote the solution of the schemes(2.15),(2.17)byand the solution of the schemes(2.16),(2.17)byrespectively.
Lemma 2.1 There exists a unique solutionof the schemes(2.15),(2.17)for any ϵ>0,n=1,···,N.
Proof. From the definition of(2.15),we know that off-diagonal elements of two linear systems of(2.17)areand therefore are symmetric.The diagonal elements are given by

By the similar argument,we get the following result.
由图1可以看出,酶解液多糖以相对分子质量100 kDa以上为主,含量达63.32%;其次为分子量小于10 kDa的多糖,含量为19.96%;相对分子量30~100 kDa及10~30 kDa之间的多糖含量相当,分别为8.4%和8.32%。此外,不同分子量的超滤膜对灵芝子实体酶解液多糖的截留率差异显著,随着膜孔径的增大,多糖截留率降低。其中,10 kDa的超滤膜对多糖的截留率约为80.12%,而30 kDa和100 kDa的超滤膜对多糖的截留率分别为71.83%和63.32%。
Lemma 2.2 There exists a unique solutionof the schemes(2.16),(2.17)for any δ>0,n=1,···,N.
Remark 2.1 Note that there would be another possible approach for time-scale discretization of(1.1)(including implicit form[16]).As for our time discretization,it is meaningful to recognize that our scheme coincides with continuous model(1.1)in the point of view of image selective smoothing.Then,our scheme would become more efficient in so far as it satisfies the properties related to image processing.
3 Stability Estimates
In this section,we give some stability estimates on the scheme in accordance with the purpose of image processing.
We use the following result(see[8,16]).
Lemma 3.1 Let Thbe a 2D mesh having simplicies with interior angles not exceeding π/2,u,v∈Vh,and w be piecewise constant on Th.Then

where

wTdenotes the value of w in T∈Th.
Now we describe our main results.
Theorem 3.1 There exists a limitN of a subsequence offor ϵ→0,whereis the solution of the schemes(2.15),(2.17)(we call it generalized solution).Moreover,for this generalized solution,the following estimates hold.
For n=1,···,N,
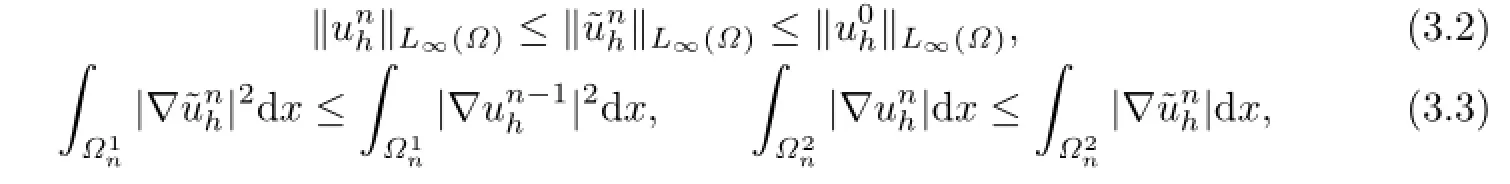
where

Especially,when f≡0(purely isotropic diffusion),

when f≡1(purely anisotropic diffusion),

Proof. We rewrite(2.17)in the form


In the same way,considering the relationships for minimum,we can obtain

Similarly,from the second equality in(3.6),we have

After all,(3.7)and(3.8)imply

Since the above inequality holds independently to the parameter ϵ,we can choose convergent subsequence ofas ϵ→∞.Denoting the limit of this subsequence byit is clear that the first estimate(3.2)of the theorem is satisfied for that.
To obtain the estimate(3.3)of the theorem,let us multiply the first equality in(2.17) byand sum it over all nodes.Then

Since the first term in the above expression is nonnegative,using the definition of an−1ij and the equality(3.1)in Lemma 3.1,we get

Using the inequality

one has

For the adequate subsequence,from Lebesgue's dominated convergence theorem,
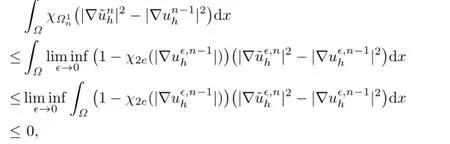
which gives the first estimate in(3.3).
In order to obtain the second estimate in(3.3),we multiply the second expression in (2.17)byand sum it over all nodes.Then we get

Considering the definition ofand(3.1)in Lemma 3.1,one has

Using the inequality

and from(3.11),we obtain

Considering the inequality
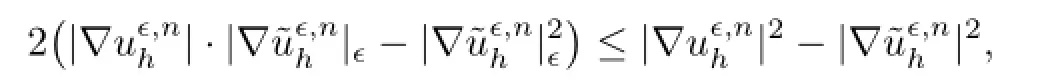
from(3.12),we obtain

Then

Applying Lebesgue's dominated convergence theorem for the adequate subsequence,we get

which gives the second estimate in(3.3).
Theorem 3.2 There exists a limit,N of a subsequence ofthe solution of the schemes(2.16),(2.17)for δ→0(we call it generalized solution).Moreover, the estimates(3.2)–(3.5)in Theorem 3.1 still hold for this generalized solution.
Proof. In the same way as in the proof of Theorem 3.1,the following inequality holds:

Therefore,we get the existence of generalized solution and the estimate(3.2).As we can see,the first estimate in(3.3)still holds for the generalized solution.
Now we prove the second estimate in(3.3).Through the same discussion as in the proof of Theorem 3.1,we can obtain

and from that

Now we set

Then from(3.15)

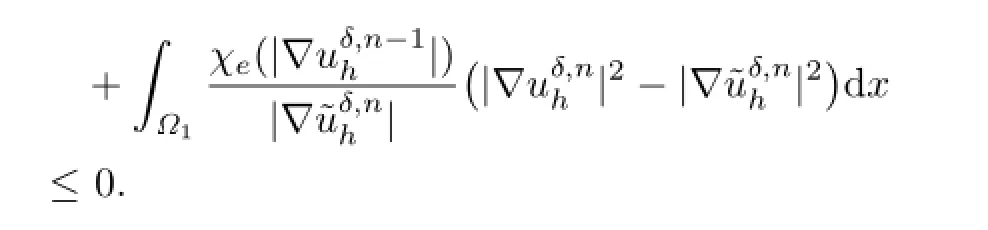
Considering the inequality

we obtain from the above inequality

Using the inequality

and from the above expression,one has

On the other hand,as δ→0(choosing a subsequence),

Applying Lebesgue's dominated convergence theorem,we obtain from(3.18)that

which gives the second estimate in(3.3).We obtain the estimates(3.4)and(3.5)in the same way as in the proof of Theorem 3.1.
Remark 3.1 Note that the stability on decay of L2,L1-norm of gradients(total variation)in subsequent time-scale steps is the property required in the image processing applications related to the image smoothing(filtration or de-noising)by the isotropic and anisotropic diffusion,respectively.
[1]Alvarez L,Lions P L,Morel J M.Image selective smoothing and edge detection by nonlinear diffusion II.SIAM J.Numer.Anal.,1992,29:845–866.
[2]Caselles V,Kimmel R,Sapiro G.Geodesic active contours.Int.J.Comput.Vis.,1997,22: 61–79.
[3]Chen Y G,Giga Y,Goto S.Uniqueness and existence of viscosity solutions of generalized mean curvature flow equations.J.Differential Geom.,1991,33:749–786.
[4]Evans L C,Spruck J.Motion of level sets by mean curvature.I.J.Differential Geom.,1991, 33:635–681.
[5]Alvarez L,Guichard F,Lions P L,Morel J M.Axioms and fundamental equations of image processing.Arch.Ration.Mech.Anal.,1993,123:199–257.
[6]Oberman A M.A convergent monotone difference scheme for motion of level sets by mean curvature.Numer.Math.,2004,99:365–379.
[7]Deckelnick K,Dziuk G,Elliott C M.Computation of geometric partial differential equations and mean curvature flow.Acta Numer.,2005,14:139–232.
[8]Handlovicova A,Mikula K,Sgallari F.Semi-implicit complementary volume scheme for solving level set like equations in image processing and curve evolution.Numer.Math.,2003,93:675–695.
[9]Mikula K,Sarti A,Sgallari F.Co-volume method for Riemannian mean curvature flow in subjective surfaces multiscale segmentation.Comput.Vis.Sci.,2006,9:23–31.
[10]Corsaro S,Mikula K,Sarti A,Sgallari F.Semi-implicit covolume method in 3D image segmentation.SIAM J.Sci.Comput.,2006,28:2248–2265.
[11]Handlovicova A,Mikula K.Stability and consistency of the semi-implicit co-volume scheme for regularized mean curvature flow equation in level set formulation.Appl.Math.,2008,53: 105–129.
[12]Eymard R,Handlovicova A,Mikula K.Study of a finite volume scheme for the regularized mean curvature flow level set equation.IMA J.Numer.Anal.,2011,31:823–846.
[13]Handlovicova A,Kotorova D.Numerical analysis of a semi-implicit DDFV scheme for the regularized curvature driven level set equation in 2D.Kybernetika,2013,49:829–854.
[14]Mikula K,Ramarosy N.Semi-implicit finite volume scheme for solving nonlinear diffusion equations in image processing.Numer.Math.,2001,89:561–590.
[15]Drblikova O,Mikula K.Convergence analysis of finite volume scheme for nonlinear tensor anisotropic diffusion in image processing.SIAM J.Numer.Anal.,2008,46:37–60.
[16]Walkington N J.Algorithms for computing motion by mean curvature.SIAM J.Numer.Anal., 1996,33:2215–2238.
A
1674-5647(2015)04-0351-11
10.13447/j.1674-5647.2015.04.07
Received date:Dec.29,2014.
The NSF(11371170)of China.
E-mail address:kkijgr@163.com(Kim K I).
2010 MR subject classification:65M60
猜你喜欢
杂志排行
Communications in Mathematical Research的其它文章
- The Representive of Metric Projection on the Finite Codimension Subspacein Banach Space
- On Weakly P.P.Rings
- Self-dual Codes with Symplectic Inner Product
- Lp-centroid Bodies and Its Characterizations
- Biquartic Finite Volume Element Method Based on Lobatto-Guass Structure
- Co-commuting Mappings of Generalized Matrix Algebras
