Self-dual Codes with Symplectic Inner Product

NAN JI-ZHU AND YU XUE-MIN

(School of Mathematical Sciences,Dalian University of Technology,Dalian,Liaoning,116024)

Communicated by Du Xian-kun

Self-dual Codes with Symplectic Inner Product

NAN JI-ZHU AND YU XUE-MIN

(School of Mathematical Sciences,Dalian University of Technology,Dalian,Liaoning,116024)

Communicated by Du Xian-kun

In this paper,we discuss a kind of Hermitian inner product—symplectic inner product,which is different from the original inner product—Euclidean inner product.According to the definition of symplectic inner product,the codes under the symplectic inner product have better properties than those under the general Hermitian inner product.Here we present the necessary and sufficient condition for judging whether a linear code C over Fpwith a generator matrix in the standard form is a symplectic self-dual code.In addition,we give a method for constructing a new symplectic self-dual codes over Fp,which is simpler than others.

symplectic inner product,symplectic self-dual code,symplectic circulant code

1 Introduction

Let Fpbe a field,where p is a prime number.Self-dual codes over Fpare an important class of linear codes,as described in[1].Kim and Lee[2]have discussed self-dual codes under Euclidean inner product or Hermitian inner product.

Now,we give a brief introduction to several basic definitions and facts in coding theory. A linear[n,k]code C over Fpis a k-dimensional vector subspace of.The element c of C is called codeword.The value n is called the length of C.

There are two normal inner products–Euclidean and Hermitian inner products.For two vectorsthe Euclidean inner product over finite field Fpis defined as

When p is an even power of any prime,we can also consider the Hermitian inner product which is defined as

The Euclidean dual code C⊥Eof C is defined as

Similarly the Hermitian dual code C⊥His defined as

We know that

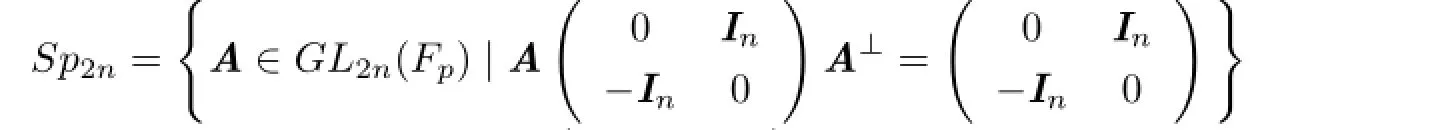
Definition 1.1 Let C be a code over Fp.The lengths of the codewords are all 2n.For two codewords x=(x1,···,x2n),y=(y1,···,y2n)∈C,we define the symplectic inner product of x,y as follows:

where yTdenotes transposed vector of y and Inis the identity matrix of order n.

Remark 1.1 The length of any codeword x∈C is 2n,since we discuss the self-dual code under symplectic inner product.

Definition 1.2 The symplectic dual code C⊥Sof C is defined as

If C⊆C⊥S,then C is called a symplectic self-orthogonal code.If C=C⊥S,then C is called a symplectic self-dual code.The necessary condition for C to be a symplectic self-dual code is that k=n(i.e.,C is a linear[2n,n]code).

In this paper,we consider the linear[2n,n]code over Fpwith a generator matrix in the standard form:G=(InA),where A is an n×n matrix over Fp.

Now we give several basic definitions(see[3]).The matrix A is called a circulant matrix, if

The form G=(InA)is called pure double circulant,where A is an n×n circulant matrix. If

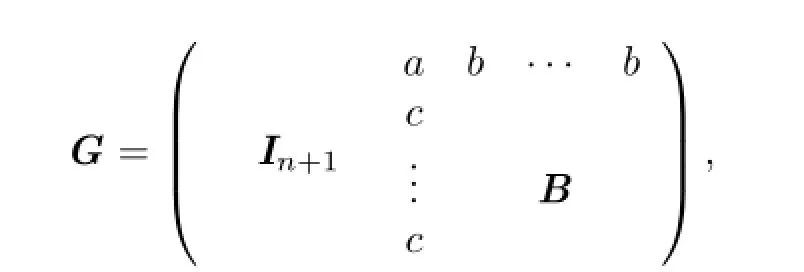
where B is a circulant matrix,then G is called bordered double circulant.Both of these codes are called double circulant codes.

2 Symplectic Self-dual Codes

In this section,we derive the necessary and sufficient condition when a code C with the generator matrix in the standard form is a symplectic self-dual code.

Lemma 2.1[4]Let C be a[2n,n]code over Fp,where n＞2.C is generated by G= (InA),where A is a circulant matrix.Then

(1) if n is a even number,C is a symplectic double circulant self-dual code if and only if(mod p)for

(2) if n is a prime number,C is a symplectic double circulant self-dual code if and only if(mod p)for

If C is a symplectic self-dual code,we have C=C⊥S.Then any two rows of the generator matrix are orthogonal to each other under the symplectic inner product.

It is easy to see that xi•xi=0 for all 1≤i≤n.

For all 1≤i,j≤n and i̸=j,

Hence

Conversely,for any y=(y1,···,y2n)∈C⊥S,we have

i.e.,

The basis solution set of above linear equations is

Then the generator matrix of C⊥Sis as follows:

Since aij≡aji(mod p)for all 1≤i,j≤n,we have

Thus C=C⊥.So C is a self-dual code.

3 Building-up Construction for Symplectic Self-dual Codes over Fp

In this section,we give the building-up construction method for symplectic self-dual codes over Fp.The complete generalization for Euclidean and Hermitian self-dual codes over finite fields Zpmwas given by[5].

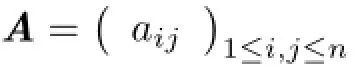
generates a symplectic self-dual code C over Fpwith length 2n+2.

Proof. It suffices to show that any two rows of G are orthogonal to each other under the symplectic inner product.Let ribe the row of the matrix G,where 1≤i≤n.

It is easy to see that any row of G is orthogonal to itself under the symplectic inner product.

For 1≤j≤n,the inner product of the first row of G with the j+1-th row equals

For 1≤i,j≤n with i̸=j,the inner product of the(i+1)-th row of G with the(j+1)-th row is equal to

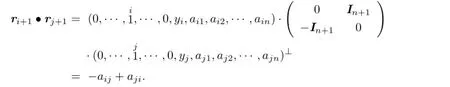
Since C0is a symplectic self-dual code,by Theorem 2.2,we have

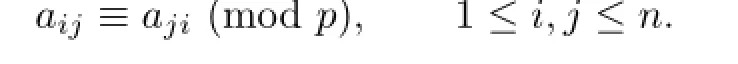
Then

so C⊆C⊥S.

Conversely,for any r=(r1,···,r2n)∈C⊥S,r is orthogonal to all rows of G.When j=0,we have

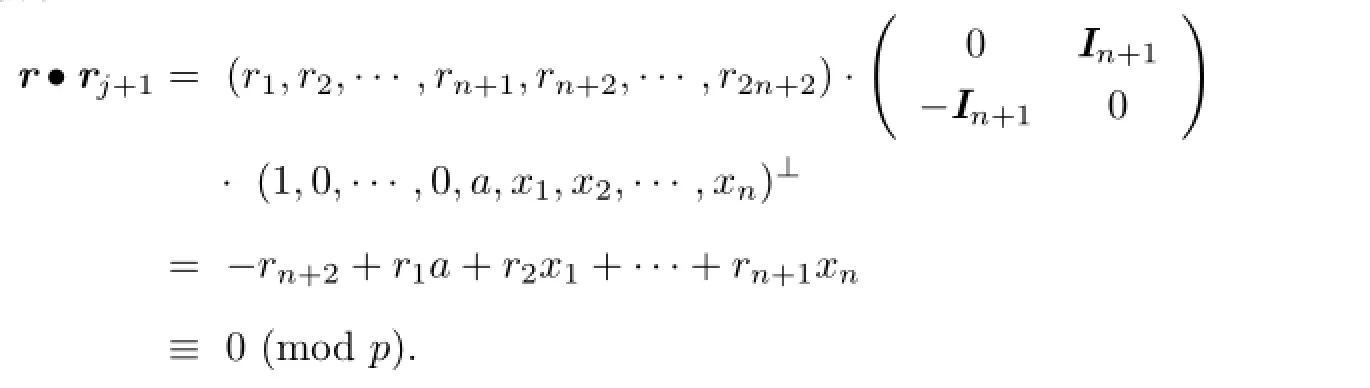
When 1≤j≤n,

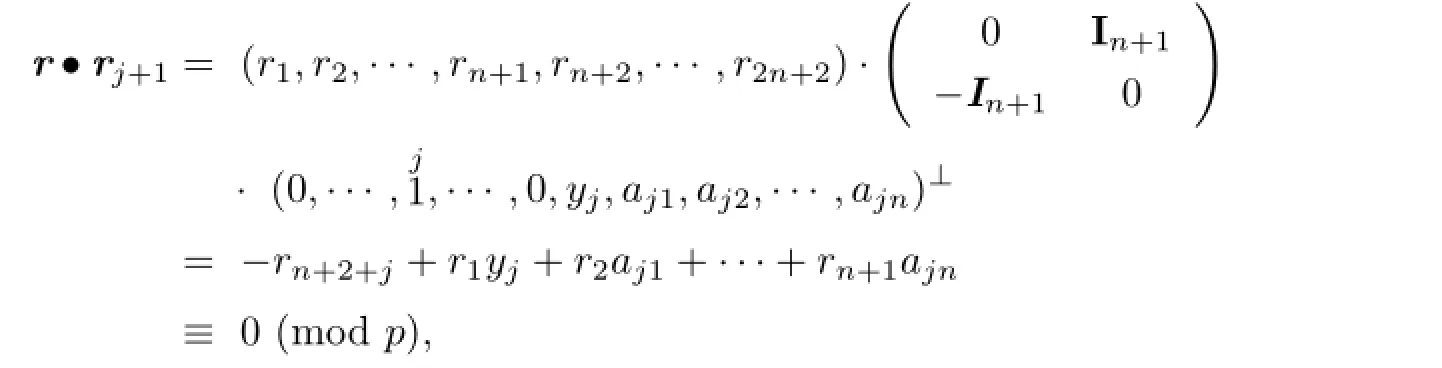
i.e.,

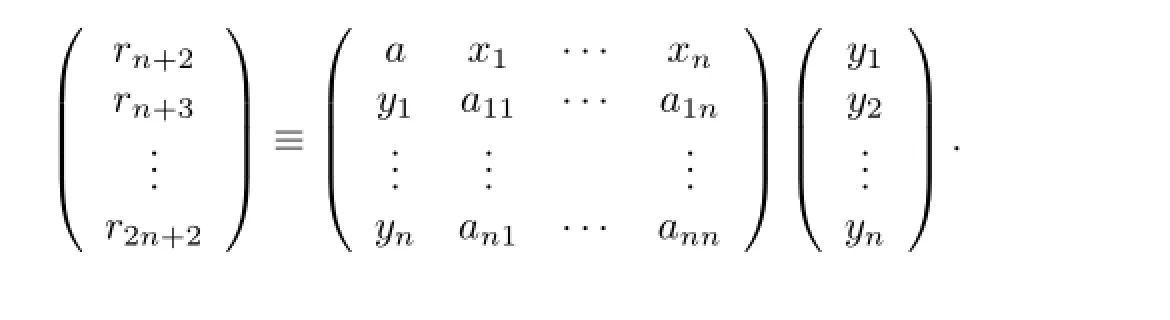
The basis solution set of the above linear equations is

Then the generator matrix of C⊥is as follows:

Since xi≡xjand aij≡aji(mod p),for all 1≤i,j≤n,we have

thus C⊆C⊥S.Therefore C is a self-dual code.

Remark 3.1 In exactly the same way as in Theorem 2.2,if the generator matrix of C is a pure double circulant,we can construct a symplectic self-dual code C1of length 2n+2 from the code C of length 2n by adding a row and two columns.And,more remarkable,if x=(b,b,···,b),y=(c,c,···,c)and b≡c(mod p),then the new code C1is a symplectic double circulant self-dual code.

[1]Nebe G,Rains E M,Sloane N J A.Self-dual Codes and Invariant Theory.Berlin:Springer, 2006:227–243.

[2]Kim J L,Lee Y.Euclidean and Hermitian self-dual MDS codes over large finite fields.J.Combin. Theory Ser.A,2004,105:79–95.

[3]Gulliver T A,Harada M,Miyabayashi H.Double circulant and quasi-twisted self-dual codes over F5and F7.Adv.Math.Comm.,2007,1(2):223–238.

[4]Wang C C.Circulant Self-dual Codes with Symplectic Inner Product.Master Thesis.Dalian: Dalian University of Technology,2010.

[5]Lee H,Lee Y.Construction of self-dual codes over finite rings Zpm.J.Combin.Theory Ser.A, 2004,105:407–422.

A

1674-5647(2015)04-0345-06

10.13447/j.1674-5647.2015.04.06

?

Received date:March 28,2014.

The NSF(11371343)of China.

E-mail address:jznan@163.com(Nan J Z).

2010 MR subject classification:94B05,51A50