基于试验任务相关的并行化关联挖掘研究

2015-11-26何国良

中国科技信息 2015年22期

何国良雷震孙岩

基于试验任务相关的并行化关联挖掘研究

何国良雷震孙岩

通过分析关联挖掘和传统Apriori算法的特征，设计并实现一种基于任务相关和布尔矩阵的并行化Apriori关联挖掘算法。该算法通过分而治之的分布式并行计算承载平台MapReduce进行计算，只需扫描一次数据库，将事务数据库转化为布尔矩阵，仅对任务相关的项集进行连接合并与向量内积运算，提升了Apriori算法的关联挖掘效率。

关联规则挖掘也称为频繁项集挖掘，旨在发现海量数据项集之间的相互关联关系。在诸多的关联挖掘算法中，Apriori算法是比较经典的算法之一。该算法结合一定的先验知识，采用逐层迭代的方法搜索频繁项集。传统的Apriori算法中，若要生成频繁项集，就要执行连接和剪枝，而这些连接和剪枝操作带有一定的机械性和盲目性，会有大量冗余的候选项集生成，需要进行多次扫描数据库操作，导致算法运行效率不高。

鉴于传统Apriori算法的以上不足，本文提出一种基于任务相关的并行化Apriori关联规则挖掘算法。该算法仅仅需要对数据库进行一次扫描操作，把原始事务数据集划分为多个数据分片，基于MapReduce并行计算平台对各个数据分片进行计算与整合，同时将项目映射为布尔矩阵，弃除与任务无关的项集，通过连接合并与向量内积计算，减少候选项集，以相应并行逻辑运算代替频繁的数据库扫描，最终完成高效的关联挖掘任务。

关联规则相关定义及Apriori算法简介

关联规则相关定义

关联规则相关定义如下:

（1）关联规则。关联规则分析最初是用来确定事务数据库中事务项之间的关联关系。设I是项目的集合，X和Y都是I的子集，并且X∩Y=Ф，关联规则是像X=＞Y这种形式的表达式。

（2）支持度（support）。是指同时包含X和Y的事务在总事务数据库中所占的百分比，即sup（X=＞Y）=P（X∪Y）；最小支持度表示项集在统计意义上的最低重要性，是由用户定义的衡量支持度的一个阈值；

（3）置信度（confidence）。是数据库中包含项目集X的事务中出现项目集Y的概率，即同时包含项目集X和项目集Y的事务与只包含X的事务数的比值，是一种条件概率，即conf（X=＞Y）=P（X∪Y）/P（X）= P（Y|X）；最小置信度表示项集在统计意义上的最低可靠性，是由用户定义的衡量置信度的一个阈值。

给定一个数据库，当一条规则满足最小支持度和最小置信度时，称该规则为强关联规则，也就是需要分析的关联规则。

Apriori算法简介

Apriori算法是一种宽度优先算法，采用逐层搜索的迭代方法挖掘频繁项集。在首轮迭代过程中，通过计算事务数据库中每一个项的支持度从而找出频繁项集。继而在前一轮生成的频繁k-项集的基础之上，将其作为本轮的种子项集，迭代产生候选（k+1）-项集，计算每个候选（k+1）-项集在事务数据库中的支持度，从而计算出所有频繁（k+1）-项集，再将其作为下轮的种子项集，按照上述方法迭代计算候选项及频繁项集，直到不再满足新的频繁项集产生条件时结束整个频繁项集挖掘过程。

根据频繁项集的定义，为了找出所有的频繁项集，需要穷举出一条事务中的所有项的各种组合和每种组合的支持度，找出频繁项集。为提高项集组合的搜索效率，Apriori算法遵循了以下两条定理:

定理1:频繁项集的任何非空子集都是频繁项集；

定理2:非频繁项集的任何超集都是非频繁项集。

任务相关

考虑到作战试验数据具有丰富的属性类别，数据量大，维数众多，这样在进行上述频繁项集提取时会有大量候选项集产生，其中很多候选项集对于挖掘目标而言是不相关的，且只会影响挖掘分析效率。如果初始阶段就能够瞄准挖掘目标，挖掘过程中紧密结合挖掘任务，允许用户交互其中，通过消减掉大量与任务无关的候选项集，只产生与任务相关的某个子集，使得挖掘过程更加具有针对性，节省支持度计算时间和存储项集的空间，以此来提高关联挖掘效率。

事务项目的布尔化及向量内积

事务项目的布尔化

事务数据库经过一次扫描之后，被映射为布尔向量矩阵。以下表为例，表1是数据库片段，表2是该片段对应的布尔向量矩阵。布尔向量中的“1”的出现的次数与该项目在数据库中出现的次数一致。

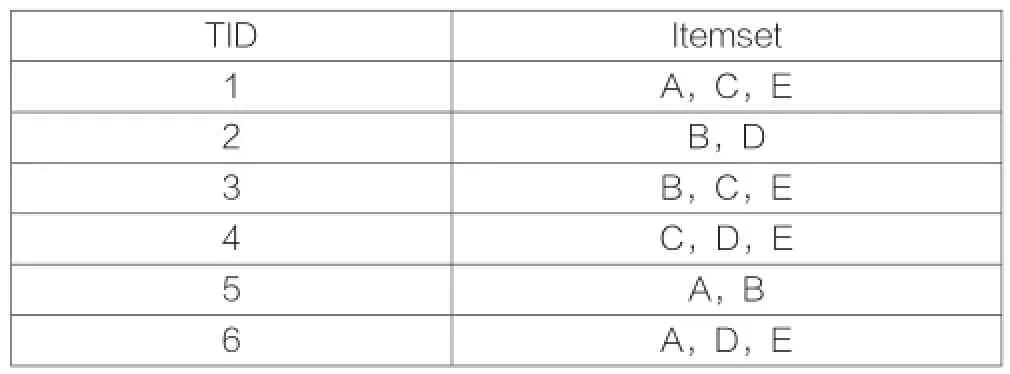
表1 数据库片段

表2 片段对应布尔向量矩阵

向量内积

关于向量空间内积，我们并不陌生。对于任意两个n维向量α=（x1，x2，…，x n）和β=（y1，y2，…，yn），其内积定义为:

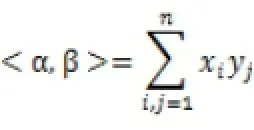
改进算法

可描述为（假设任务相关项个数为1）

步骤1:原始事务数据集被划分为多个数据分片，对各个数据分片进行扫描，将其映射为一个布尔向量矩阵。

步骤2:频繁1项集推导。在Map阶段，对各分片中各项目中“1”的个数进行统计；在Reduce阶段，对所有Map阶段输出的结果进行合并，获取全局候选1-项集，并且和MinSup进行比较，输出符合要求的频繁1-项集。

步骤3:频繁2项集推导。在Map阶段，对频繁1项集中任务相关的任意2个向量进行内积运算，得到候选2-项集；在Reduce阶段，对所有Map阶段输出的结果进行统计，判断结果中“1”的个数是否满足支持度阀值条件，如果满足则将此2个向量组合判断为频繁2项集。

步骤4:频繁k（k≥3）项集推导。在Map阶段对前述已存在的频繁k-1（k≥3）项集中任意两个符合条件的任务相关项集进行连接操作，从而生成k项集，在生成结果中判断不同的两个项的内积；在Reduce阶段对所有Map阶段输出的结果进行合并，结果符合支持度阀值的则可继续进行下一步，否则该k-项集不属于频繁k项集的考虑范畴。

步骤5:如果上述在Reduce阶段符合支持度阀值的k项集的所有k-1项子集都存在于频繁Lk-1中，那么进入下一步；如果有一项子集不存在于频繁Lk-1中，根据性质“非频繁项集的任何超集都是非频繁的”，则该k-项集也不属于频繁项集。

步骤6:在Map阶段，对该k项集的所有任务相关项目进行内积运算；在Reduce阶段，统计所有Map阶段的输出结果，符合支持度阀值要求的k项集被判断为频繁k项集。

按照上述过程求出全部频繁项集。

算法性能分析

本实验采用3台虚拟机组成集群环境，虚拟机运行在高性能刀片服务器上，该服务器支持多核英特尔®至强TM处理器5600系列。其中一台虚拟机作为主服务器（Master），其余2台作为从服务器（Slave）。设定每台虚拟机的IP地址并使用48口千兆交换机互联。

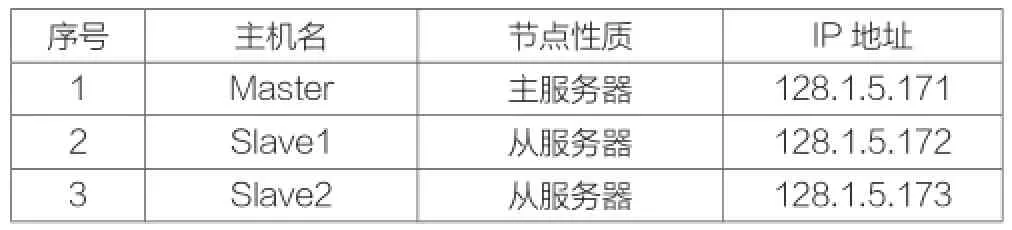
表3 Hadoop集群配置信息

首先在客户端Windows平台下安装Citrix XenCenter软件，在该环境下创建虚拟机并在虚拟机上安装CentOS操作系统和JDK，创建Hadoop用户，配置SSH和Hadoop环境，安装Navicat for MySQL数据库（版本号是8.2.20）。使用Eclipse进行程序设计与调试。采用UC Irvine 机器学习数据仓库中的mushroom数据库作为实验对象，该数据库共有8124条记录，部分记录如图1所示。

运行结果如图2所示。

相比传统Apriori算法，本文提出的基于试验任务相关的并行化改进Apriori算法效率提升明显。

图1 mushroom数据库（片段）

图2 算法性能对比

结语

本文提出的基于试验任务相关的并行化关联挖掘算法是在传统Apriori算法的基础之上改进的，原始事务数据集被划分为多个数据分片，将其映射为布尔向量矩阵，对各个数据分片分别进行扫描和并行化处理，仅需扫描一次数据库，且通过消减掉大量与任务无关的候选项集，只产生与任务相关的某个子集，显著提升了传统Apriori算法的关联挖掘效率。