纳米磁流体动态散斑干涉场的奇异场分布

王希军

(中国科学院长春光学精密机械与物理研究所应用光学国家重点实验室，吉林长春130033)

1 引言

激光散斑测量技术具有测量精度高、非接触、全场、实时性和对环境要求低等优点，广泛应用于速度、振动、位移、应力、应变、表面粗糙度测量等领域［1-6］。随着人们对激光散斑场的统计性质认识的深入，激光散斑场强分布中相位奇异点的发现，更是激光散斑研究对光学理论的重大贡献。

散斑图像中，光强零值点处的相位不能确定，光强零值点称为相位奇异点，又称为光学涡旋(optical vortex)，相位奇异点(Singularities)也叫奇异场(Singular optical field)［7-9］。理论和实验证明激光散斑场中散斑颗粒和光强零点的个数相等，所以在散斑场中有大量的奇异场。奇异场均成对出现，奇异场的位置分布可以反映散斑颗粒的分布，奇异场同时也决定着散斑分布的结构［10-11］。

全息图像通过激光照射到全息位相板，形成传播的全息场，可在一个精密位相扫描平移台上由摄像机接收，并计算出光束中暗场的分布。2004年，Nature报道了英国格拉斯哥大学Padgett小组发现的激光散斑中奇异场的环结构造现象，激光光束暗场可以操纵稳定的光学涡旋结［12］。此外，许多研究利用计算机模拟全息位相图，得到涡旋光束，再用涡旋光束照射，获得透射散斑，进而分析了光场的分布情况［13］。

2007年，Physical Review Letters又报道了Padgett小组提出了光场散斑中的奇异场分形处理方法，尤其是暗场的分形表述，进一步说明光学暗场中的统计复杂性具有简单多次重复的特性。这项研究找出激光光场中散斑形成的光学涡旋，不间断地找到光场奇异点，描绘出空间奇异场的分布，最后用分形理论解释了激光散斑的奇异性。因此，该项研究开拓了激光散斑从统计光学向复杂系统的最简规范的发展道路［14］。

本文从激光双扫描散斑干涉实验中获得的动态散斑干涉图出发，利用奇异场计算方法，计算出散斑光场的相位涡旋分布及其变化特征。在计算动态激光散斑干涉图的奇异点的基础上，分析和讨论了奇异场分布变化和散斑变化过程的对应关系。

2 散斑奇异场计算

在纳米磁流体双扫描动态散斑干涉实验中，通过光电图像探测器获得的散斑图像是激光散斑的光强分布。因此，散斑光强需要通过各向同性的拉盖尔-高斯变换，构造出与散斑场对应的复场强，从而获得散斑场的奇异场分布描述［15-16］。

令 g(x，y)为散斑的强度分布，G(fx，fy)为其相应的傅里叶频谱，则经过拉盖尔-高斯滤波器，得到 g(x，y)及对应的各向同性复函数)公式:

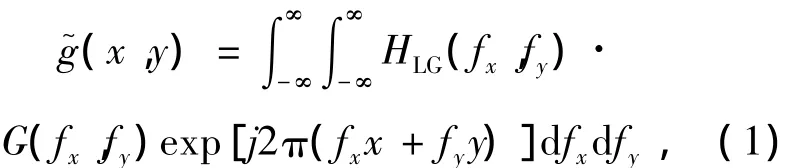
式中，HLG(fx，fy)是拉盖尔-高斯滤波函数，在频域为:

拉盖尔-高斯滤波器的振幅是螺旋结构，抑制了导致不稳定的奇异场的高频成分。因此，选择合适的拉盖尔-高斯滤波带宽，保证与原散斑图像中的散斑大小相适应的散斑涡旋密度。得到，

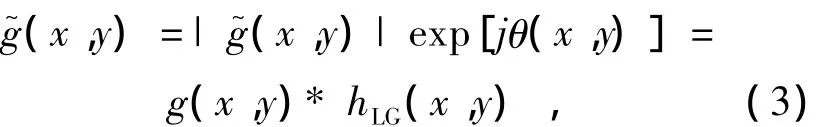
式中，*为卷积算符，hLG(x，y)是空域中的拉盖尔-高斯滤波函数，为，

式中，F-1为逆傅里叶变换，(r，α)是(x，y)对应的极坐标。散斑的相位奇异计算如图1所示。

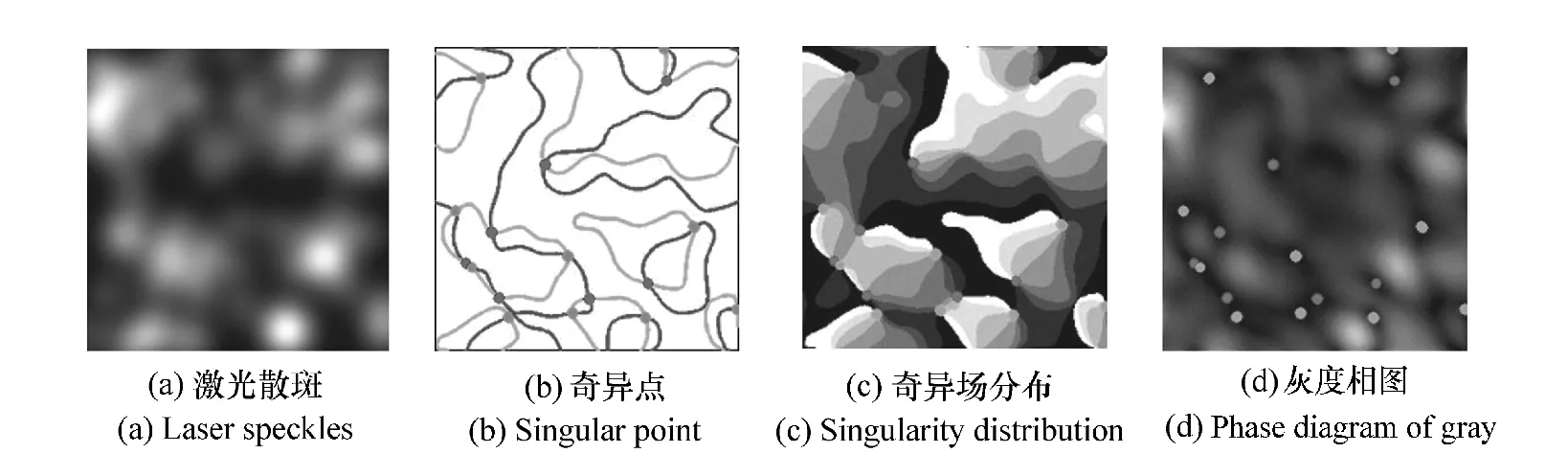
图1 激光散斑光场及奇异场分布Fig.1 Optical intensity and singularity field distribution of laser speckles

图1(a)为散斑图样的光强分布。根据式(4)，利用MATLAB提取出散斑图像的相位奇异场分布，如图1(b)～1(d)所示。

图1(b)为其实部零值线和虚部零值线的分布，两线的相交的点为相位奇点，其相位无法确定。相位在这些交点处发生突变。从相位奇点都向外延伸出一系列等相线，且在该点附近环绕其一周的相位都是在-π到π范围内，半周递增，半周递减。

图1(c)为图1(a)散斑场的相位分布，图1(c)中灰度从黑至白代表相位的取值范围是从-π变化到π，将相位奇异点周围的相位分成8个区域。从每个奇异场辐射出8条等相线，每条等相线代表区间(-π，π］上的一个相位值，相邻等相线的相位值相差π/4，从中清晰地看出相位奇点周围相位的增加方向。

根据相位递增的环绕方向来确定涡旋的符号:如果相位绕奇点沿逆时针方向递增，为正涡旋，反之若沿顺时针方向递增则为负涡旋。图1(b)～1(d)中，红色圆点代表正涡旋，绿色圆点表示负涡旋。

图1(d)为图1(a)对应的灰度相图，图1(d)散斑场复振幅的实部零值线和虚部零值线在空间上相交构成若干个交点。黑色表示相位涡旋区域，白色表示涡旋消隐减弱区域，灰度表示左旋和右旋作用的强弱程度。由此涡旋密度对应着光场中暗场分布位相的交替变化强弱。对于散斑场而言，涡旋密度对应散斑场中散斑的变化，是建立散斑图涡旋密度和光场磁微粒作用动态散斑变化的依据。

3 实验

为了研究磁流体的运动特性，设计了如图2所示的动态散斑实验装置，氦氖激光器发出的激光经准直后以45°的角入射到磁流体显示器件表面的磁流体薄膜上，面阵探测器在垂直方向接收散斑图像，从而降低磁流体液面及器件表面反射光的影响。

实验中所用的 He-Ne激光器，波长为632.8 nm，功率为5 mW。实验中所用的磁流体样品为煤油载液铁磁流体，磁流体的特征尺寸30～50 nm。磁流体被均匀的涂在显示器件表面上，薄膜厚度约为20 μm，受磁场控制发生聚集和分散两个过程。施加磁场时，磁流体中悬浮的纳米磁微粒开始运动，向磁场方向聚集;去除磁场时，磁流体中的纳米磁微粒在液体中均匀分散。

图2 磁流体动态散斑干涉实验光路图Fig.2 Dynamic speckle interferometry experiment of the magnet fluid

图2中的CCD记录磁流体的系列动态散斑变化，如图3(a)～3(f)所示。相邻散斑图间的时间间隔为40 ms。

4 结果与讨论

激光散斑场中的光场分布与散射表面构造密切相关:散射表面越粗糙，散斑光场越是大颗粒，散斑图像为离散分布，散斑密度越低。反之，散射表面越细密，散斑光场越是小颗粒，散斑图像为均匀分布，散斑密度越高。Goodman的统计光学完整地描述了散斑的随机特征与对比度的关系，成功地解释了散斑对光学成像的影响，并建立了成像系统的散斑控制模型［7］。

图3 纳米磁流体的动态散斑图Fig.3 Dynamic speckle of the magnet fluid

图4 动态散斑实验中的奇异场分布Fig.4 Singularity distribution of the dynamic speckles in the magnetic fluid interferometry

Goodman指出光场傅里叶变换下的实部虚部同时为零，光场位相不确定，是光场的奇异点;在奇异点附近的场强位相分布呈现旋度不为零现象，统称为光学涡旋。因此，使用式(1)～(4)计算图2实验得到的动态散斑干涉场强分布(如图3所示)，得到图4和图3对应的灰度相图。图3的散斑场复振幅的实部零值线和虚部零值线在空间上相交构成若干个交点，红色的圆点表示右涡旋的相位奇点，绿色“×”为左涡旋相位奇点。图4(a)～4(f)和图3(a)～3(f)同义。

黑色表示相位涡旋区域，白色表示涡旋消隐减弱区域，灰度表示左旋和右旋作用的强弱程度。由此，涡旋密度对应着光场中暗场分布位相的交替变化强弱。

首先灰度相图(图4)多处出现白色环状分布，大致对应散斑强场的轮廓。其次，由于干涉条纹对比度较低，在灰度相图上，界限较为模糊，可是从奇异点分布上，还保留了条纹的痕迹，显示出从左上角到右下角的排列。

图4(a)和4(b)相对像素截取的奇异点局域放大图，如图5所示。相邻的散斑拉盖尔-高斯滤波器下变换后的相位涡旋，可看到奇异场分布整体向上位移。同样对比分析也可以在图4(e)和4(f)中看到，移动的方向是下移。这个奇异场分布上观察到的移动，是因为纳米磁微粒及其团族的运动，引起了动态散斑的移动。因此，散斑对应的奇异场分布变化，对应着散斑的运动趋势。

图5 动态散斑的局域奇异场位移Fig.5 Local singularity distribution of the dynamic speckles

图4灰度相图，光学涡旋或奇异点，存在于散斑暗场中。对场强做拉盖尔-高斯滤波下的傅里叶变换，很容易得到奇异场分布。奇异点的整体构成表示出光场中的奇异场变化及分布。这里初步采用涡旋密度进行计算，是光学涡旋总数和总像素比值。

点对应着散斑场光强为零的区域，由图4计算动态散斑光场的奇异点总数，分为左涡旋数和右旋数，如表1所示。

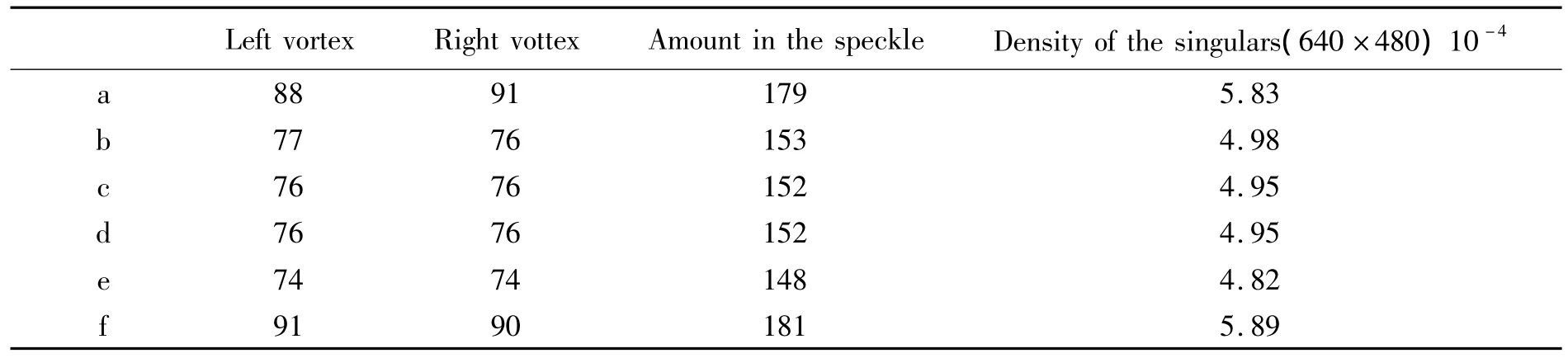
表1 散斑光场奇异点的分布密度Tab.1 Distribution density of singularity in the speckle field

奇异点密度高，散斑光场的“暗场”区域较多;奇异点密度低，散斑光场的“暗场”区域较少。在纳米磁流体激光散斑的动态系列中，表1中的涡旋密度有先大后小，再由小变大的两个微小变化，对应着纳米磁微粒引起的散斑粗糙，后又趋稳的过程。

因此，磁流体运动过程中，图4(a)和4(f)的密度相对高，说明经过外场驱动下，磁流体处于稳态状况。图4(b)和4(e)的密度相对低，对应着磁流体激烈的运动，形成较大颗粒的散斑场。

5 结论

通过研究激光散斑拉盖尔-高斯滤波器下变换后的相位涡旋分布，能够清楚地描述动态散斑暗场物理性质，突显了光场的暗场相位结构及变化趋势，特别是纳米团族引起的奇异点分布变化较为明显，为进一步定量研究动态激光散斑场的暗场变化规律提供了基础。

通过光学相位涡旋分析动态散斑场相位奇异点分布的方法，能够突出由纳米磁微粒运动引起的散斑变化及纳米磁微粒的运动能力，散斑光场的奇异分布表明了纳米引起的散斑变化趋势。散斑实验中纳米微粒团族的运动，表现在左旋右旋数目的变化过程，以及涡旋密度的变化过程。研究结果为进一步利用光场的奇异点分布描述散斑场变化的统计性质，以及纳米磁流体运动方式的转变过程的区域跟踪提供了分析手段。

奇异场分布是激光散斑特有现象，也是解释散斑场的有力工具。通过左旋和右旋及涡旋密度的变化，证明了处理动态激光散斑图像的有效性，为更好地认识激光和物质作用产生的光场的本质提供了新的思路。

［1］ PRADILLE C，BELLET M，CHASTEL Y.A laser speckle method for measuring displacement field.application to resistance heating tensile test on steel［J］.Applied Mechanics and Materials，2010，24-25:135-140.

［2］ 项阳，郭玉彬，陈波，等.一种检测超光滑表面粗糙度方法的初步研究［J］.光散射学报，1996，8(3):168-173.XIANG Y，GUO Y B，CHEN B，et al..Study on the soft X-ray total integral scattering method to study surface roughness of supersmooth surface［J］.Chinese J.Light Scattering，1996，8(3):168-173.(in Chinese)

［3］ 王希军.激光散斑的亚像素位移法计算及比较［J］.中国光学，2012，5(6):652-657.WANG X J.The laser speckle computation and comparison with the sub-pixel measurement methods［J］.Chinese Optics，2012，5(6):652-657.(in Chinese)

［4］ JAKOBSEN M L H.Distance measurements by speckle correlation of objective speckle patterns，structured by the illumination［J］.Applied Optics，2012，51(19):4316.

［5］ 王永红，李骏睿，孙建飞，等.散斑干涉相位条纹图的频域滤波处理［J］.中国光学，2014，7(3):389-295.WANG Y H，LI J R，SUN J F，et al..Frequency domain filtering for phase fringe patters of digital speckle pattern interferometry［J］.Chinese Optics，2014，7(3):389-295.(in Chinese)

［6］ 潘锋，闫贝贝，肖文，等.基于数学形态学的数字全息再现像融合方法［J］.中国光学，2015，8(1):60-67.PENG F，YAN B B，XIAO W，et al..Digital holographic re construction image fusion based on mathematical morphology［J］.Chinese Optics，2015，8(1):60-67.(in Chinese)

［7］ GOODMAN J W.Speckle Phenomena in Optics:Theory and Applications［M］.Greenwood Village:Roberts＆ Co.，2006.

［8］ RUBEN G，PAGANIN D M.Phase vortices from a Young's three-pinhole interferometer［J］.Physical Review E，2007，75(6):66613.

［9］ GALVEZ E J，SMILEY N，FERNANDES N.Composite optical vortices formed by collinear Laguerre-Gauss beams［C］.Proc.SPIE 6131，San Jose，USA，January，21，2006.

［10］ WANG W，ISHII N，HANSON S G，et al..Phase singularities in analytic signal of white-light speckle pattern with application to micro-displacement measurement［J］.Opt.Commun.，2005，248(21):59-68.

［11］ WANG W，QIAO Y，ISHIJIMA R，et al..Constellation of phase singularities in a speckle-like pattern for optical vortex metrology applied to biological kinematic analysis［J］.Opt.Express，2008，16(39):13908-13917.

［12］ LEACH J，DENNIS M R，COURTIAL J，et al..Vortex knots in light［J］.Nature(London)，2004，432，165(11 November online).

［13］ 李新忠，田晓敏，王辉，等.拉盖尔-高斯光束照射产生散斑场的特性研究［J］.光学学报，2015，35(7):0726001.LI X ZH，TIAN X M，WANG H，et al..Study on properties of speckle field formed by laguerre-gaussian beam illumination［J］.Acta Optica Sinica，2015，35(7):0726001.(in Chinese)

［14］ O'HOLLERAN K，DENNIS M R，FLOSSMANN F，et al..Fractality of light's darkness［J］.Physical Review Letters，2008，100(5):053902(4).

［15］ WANG W，YOKOZEKI T，ISHIJIMA R，et al..Optical vortex metrology based on the core structures of phase singularities in Laguerre-Gauss transform of a speckle pattern［J］.Optics Express，2006，14(22):10195-10206.

［16］ MAHÉ G，DURAND S，HUMEAU A，et al..Air movements interfere with laser speckle contrast imaging recordings［J］.Lasers in Medical Science，2012，27(5):1073-1076.