模糊控制在武装机器人稳定平台中的应用

孙钟阜

（海军驻上海地区水声导航系统军事代表室，上海201108）

模糊控制在武装机器人稳定平台中的应用

孙钟阜

（海军驻上海地区水声导航系统军事代表室，上海201108）

针对武装机器人武器平台操控稳定性的应用需求，提出了模糊控制在武装机器人武器平台稳定操控中的应用问题。在以往对稳定平台动力学规律分析的基础上，提取两自由度稳定平台的输入输出变量，利用ADAMS建立稳定平台的数学模型，将ADAMS中建立的稳定平台模型导入到Matlab中，按照稳定平台的动力学规律设计模糊控制器，通过Matlab/Simulink建立稳定平台的模糊控制系统框图，通过仿真计算，分析稳定平台在阶跃力矩信号下的响应特性，修改完善控制系统。并给出了优化后控制系统的Matlab和ADAMS联合仿真结果，结果表明，设计的模糊控制器在武装机器人武器平台稳定控制中具有良好的控制效果。

稳定平台；模糊控制器；联合仿真

进入21世纪以来，随着现代科学技术的发展，现代军事发生了极大的变化，特别是移动武装机器人的诞生使得人类将有可能从未来的战争中解脱出来［1］。本研究着重讨论陆上武装机器人，陆上武装机器人一般在野外复杂环境下执行任务，工作环境比较恶劣，这就要求必须为武装机器人配备控制性能较好的稳定平台，实现机器人在行驶过程中保持一定精度的水平稳定性和方位跟踪能力［2-3］。

随着科技的发展，部队对稳定平台控制系统提出了高精度、快速的响应速度等要求。传统的PID控制是基于偏差大小输出控制力，原理上就存在偏差，同时由于控制系统的非线性时变强耦合等特征，参数固定不变的传统PID控制越来越满足不了新的控制要求。这就为模糊控制等一系列的智能控制技术的诞生提供了现实的需求［4］。

模糊控制理论的诞生在现代控制领域具有里程碑意义。鉴于作战环境的复杂性，武装机器人在野外作战的平台控制不可能是线性的，需要具有一定智能的模糊控制。模糊控制把控制对象作为“黑箱”，将人们对“黑箱”的操作经验用现实生活中的语言表达出来，并设计成“模糊规则”，让计算机通过这些“模糊规则”模仿人类的决策过程，从而实现对被控对象的模糊控制。

为了达到较好的控制效果，模糊控制理论给出了一套系统而有效的方法，可以方便地将人们现实中使用的自然语言转换成计算机可以识别和处理的机器语言。模糊控制器是一种基于自然语言控制规则、模糊逻辑推理的计算机控制技术，它不需要知道控制系统的数学模型，而只依赖于操作者的经验，将表达知识转化成“模糊规则”，设计简单，抗干扰能力强，响应速度快，对系统参数的变化有较强的鲁棒性，属于一种智能控制［5］。

本研究针对模糊控制算法在稳定平台中的应用进行了仿真研究，使用ADAMS建立武装机器人稳定平台的机械模型（本文研究两自由度稳定平台），利用Matlab的Simulink模块建立稳定平台的控制模型并进行控制仿真［6-7］。仿真结果表明模糊控制在武装机器人稳定平台的应用中具有较好的控制效果。

1 稳定平台ADAMS模型

1.1 虚拟样机技术

虚拟样机技术——ADAMS（automatic dynamic analysis of mechanical system）全称是机械系统自动动力学分析软件，它是目前世界范围内应用非常广泛的多体系统仿真分析软件。ADAMS软件使用交互式图形环境和零件库、约束库、力库，创建完全参数化的机械系统几何模型，其求解器采用多刚体系统动力学理论中的拉格朗日方程方法，建立系统动力学方程，对虚拟机械系统进行静力学、运动学和动力学分析，输出位移、速度、加速度和反作用力曲线。ADAMS软件的仿真可用于预测机械系统的性能、运动范围、碰撞检测、峰值载荷以及计算有限元的输入载荷等。

ADAMS一方面是虚拟样机分析的应用软件，用户可以运用该软件非常方便地对虚拟机械系统进行静力学、运动学和动力学分析。另一方面，又是虚拟样机分析开发工具，其开放性的程序结构和多种接口，可以成为特殊行业用户进行特殊类型虚拟样机分析的二次开发工具平台［8-9］。

1.2 建立稳定平台模型

在ADMAS中建立稳定平台的模型如图1所示。该模型包括支架、外框和内框3部分，支架与地面固连在一起。建立各部件之间的约束关系，支架与外框建立Cylindrical约束关系，外框与内框建立Cylindrical约束关系。在稳定平台各关节之间建立驱动元件（本文使用力矩），分别作用于稳定平台的内框和外框。

图1 稳定平台模型

1.3 确定输入输出变量

稳定平台的建模过程中除了需要建立模型，添加约束和驱动力矩外，还需要建立输入输出变量，这些变量是实现ADAMS和Matlab联合仿真的中介。在ADAMS中定义驱动力矩T1和T2作为其输入变量，同时ADAMS中的输入变量又是Matlab的输出变量；在ADAMS中定义外框的横滚角φ，角速度，内框的俯仰角θ，角速度作为其输出变量，同时ADAMS中的输出变量又是Matlab的输入变量。

2 模糊控制器的设计

2.1 精确量转化成模糊量

将精确的参数离散化，将它分成若干段，每一段对应一个模糊子集，每一个模糊子集运用模糊语言表示如下：NB（负大），NS（负小），ZE（零），PS（正小），PB（正大）。某个精确的参数属于某一个模糊子集的程度用隶属度表示，而隶属度可以通过隶属函数计算出来。隶属度函数比较常用的有三角型、梯形、高斯型、和钟型。三角型函数表达式为

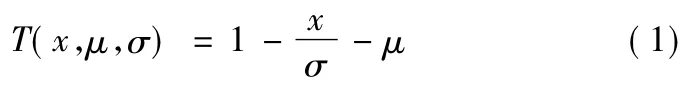
式中：μ为三角形中心值；2σ为三角形底宽。

高斯型函数表达式为

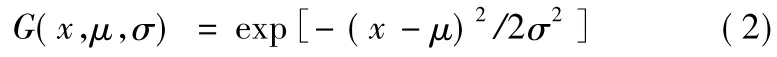
式中：μ为中心值；2σ为标准偏差。

2.2 模糊控制规则

模糊控制规则是模糊控制器的核心，体现了任何模糊控制算法的“智力”，通常根据经验和理论模拟确定，是设计者知识和经验的表现形式［10-11］。其正确性可通过试验来验证和调整。Mamdani型模糊控制算法表示为

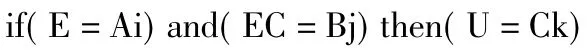
其中，E、EC、U表示语言变量。本文具体表示为角度、角速度和力矩输出。其中，E、EC在论域中所取的语言值为｛NB、NS、ZE、PS、PB｝，对应为负大、负小、零、正小、正大。U在论域中所取的语言变量为｛NB、NM、NS、NZE、ZE、PZE、PS、NM、PB｝，对应于负大、负中、负小、零、正小、正中、正大。根据稳定平台的具体要求，使用Mamdani型规则，经过多次仿真，最终得到控制效果较理想的模糊规则表，如表1所示。

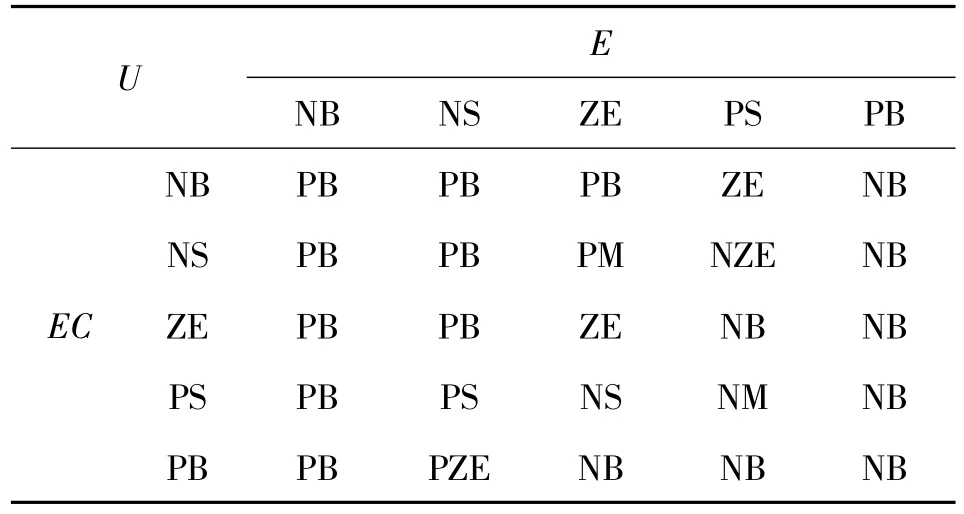
表1 模糊规则表

2.3 解模糊

解模糊是指将模糊量转化为精确值的过程。通常反模糊化的方法有3种：中位数法、最大隶属度法和加权平均法，其中最常用的是加权平均法。在实际的应用过程中，应该通过具体的情况来确定采用哪一种解模糊方法。根据稳定平台的具体设计要求，本文采用加权平均法来进行解模糊化处理，加权平均法为

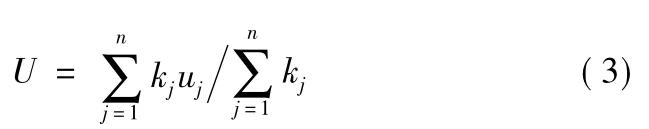
式中：kj为加权系数，通常可以选择隶属度函数作为加权系数，通常根据经验确定。

3 Matlab控制模块的建立

3.1 虚拟模型的导入

Simulink首先需要将ADAMS中的数据模型文件拷贝到Matlab的工作空间中，然后在Matlab中输入该模型文件的名称（本文中为wendingpingtai.m），就可以将稳定平台的数学模型导入到Matlab中。使用Matlab和ADAMS的连接指令adams_sys，可以获得Matlab使用的虚拟样机的模型数据。如图2为稳定平台的虚拟模型。

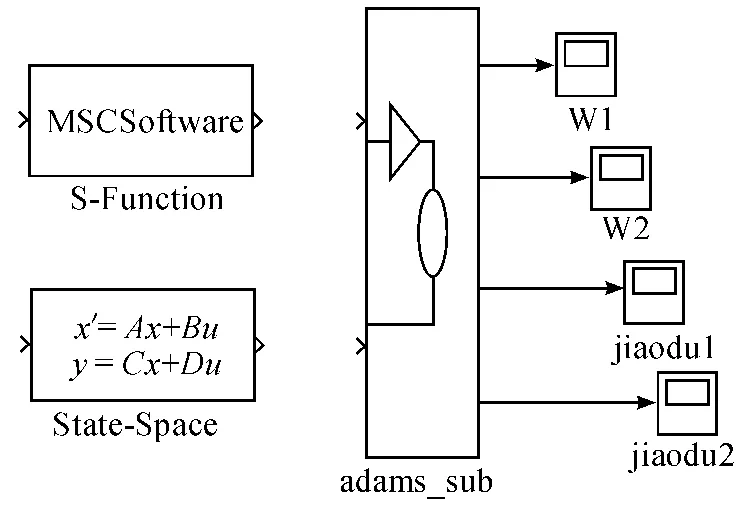
图2 Matlab中的稳定平台模型

3.2 稳定平台模糊控制框图的设计

本文模糊控制逻辑设置的内容如表2所示。选取模糊控制器角度的方法为高斯函数法和三角形函数法相结合的方法，如图3所示。角速度输入和模糊控制器的输出均采用三角形函数法，如图4、图5所示。模糊控制框图如图6所示。

表2 模糊控制逻辑

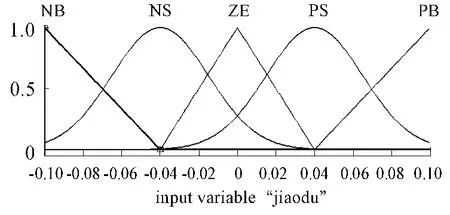
图3 角度输入的隶属度函数

图4 角速度输入的隶属度函数

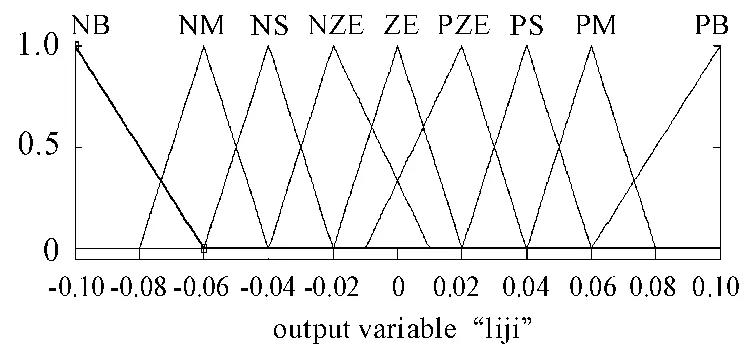
图5 力矩输出的隶属度函数

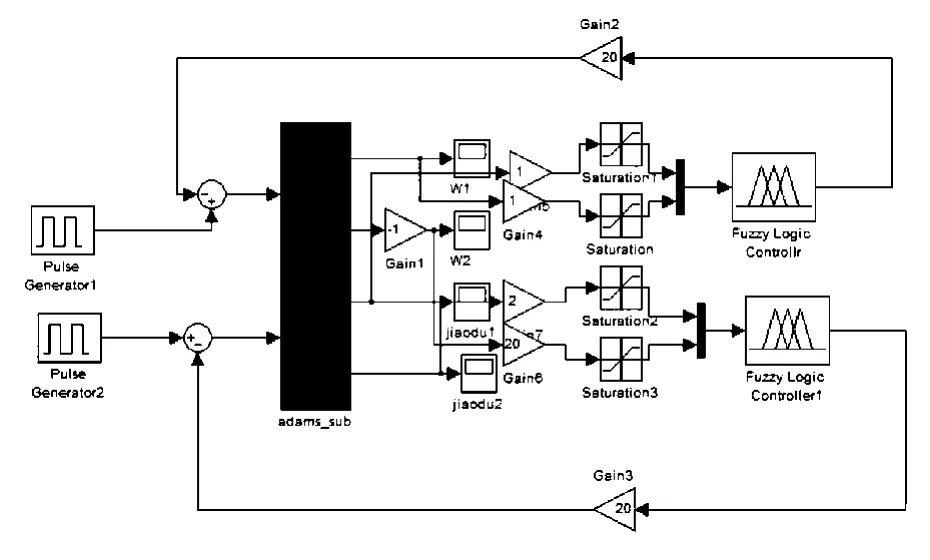
图6 模糊控制框图

3.3 仿真过程及结果

针对稳定平台进行自稳定控制的实际情况进行仿真，即稳定平台跟随载体有连续的位置变化。对两自由度稳定平台的横滚环和俯仰环分别加入阶跃信号扰动，观察稳定平台在扰动信号作用下的运行情况。稳定平台控制系统脉冲响应如图7和图8所示。在模糊控制器的作用下，稳定平台能在短时间内达到稳定，其跟踪误差较小，仿真结果表明模糊控制器在稳定平台的自稳定中具有很好的控制效果。

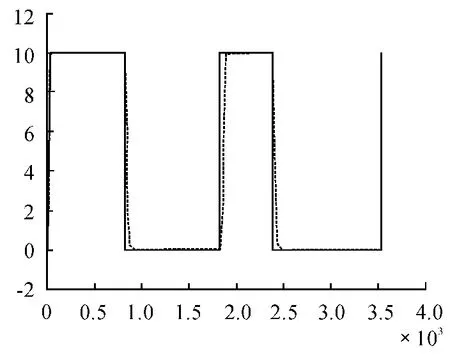
图7 横滚框阶跃信号下的响应图

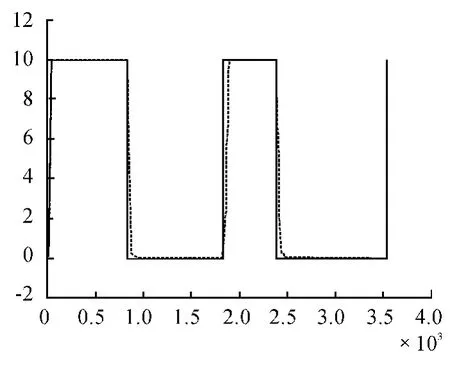
图8 俯仰框在阶跃信号下的响应图

4 结论

本研究采用模糊控制器对陆上武装机器人两自由度稳定平台的横滚环和俯仰环进行控制，并在ADAMS和Matlab环境下进行了联合仿真，通过联合仿真的结果可以说明这种模糊控制器能够很好地对两轴稳定平台进行自稳定控制，为今后对未知模型或难以获得传递函数的模型进行控制打下较好的基础。ADAMS与Matlab在此次仿真中可以很好地发挥2个软件的各自优势，ADAMS建模可以很快地获得系统的传递函数，同时又可以避免复杂的数学推导过程，Matlab具有强大的控制仿真能力，同时联合仿真的结果既清晰又直观。当ADAMS和Matlab的联合仿真运用到更加复杂的仿真时，这种方法的优势将更加明显，具有非常重要的现实意义。

［1］仲崇慧，贾喜花.国外地面无人作战平台军用机器人发展概况［J］.机器人技术与应用，2005（4）:18-24.

［2］江伟伟.遗传算法在武装机器人稳定平台控制中的应用［J］.四川兵工学报，2014，35（10）:41-47.

［3］高翌阳，齐蓉.舰载天线稳定平台伺服控制器研究［J］.计算机测量与控制，2012，20（5）:1301-1306.

［4］姜丽辉，周长省.惯性稳定平台位置伺服的模糊控制仿真研究［J］.微机电，2014，47（7）:67-71.

［5］毕永利，王中鲜.模糊控制在光电稳定平台跟踪中的应用［J］.黑龙江水专学报，2010，37（2）:94-96.

［6］应再恩，平雪良.基于ADAMS和Matlab的双回路PID控制倒立摆联合仿真［J］.机械传动，2012，36（8）:64 -67.

［7］Han Y，Tzoneva R.Matlab，Labview and FPGA Linear Control of an Inverted Pendulum［C］//AFRICON 2007.［S. l.］:［s.n.］，2007:1-7.

［8］陈文凯，莫亚武.三自由度并联机器人动力学及仿真［J］.机械传动，2009，33（1）:25-27.

［9］王建平，彭凯.基于ADAMS的一种新型六自由度并联机构的参数分析与仿真［J］.机械传动，2011，35（5）:31 -35.

［10］姜丽辉，周长省.惯性稳定平台位置伺服的模糊控制仿真研究［J］.微电机，2014，47（7）:67-71.

［11］邱宝梅，王凤娟.基于模糊-PID控制的小型机载摄影稳定平台［J］.光电工程，2010，37（10）:23-28.

［12］苏豪，薛方正.关节型机器人通用仿真平台设计［J］.重庆理工大学学报:自然科学版，2012（6）:82-88.

（责任编辑周江川）

Application of Fuzzy Control on Armed Robot's Turntable

SUN Zhong-fu
（The Navy Military Agent's Room of Acoustic Navigation System in Shanghai Area，Shanghai 201108，China）

According to the armed robot stable platform application，the problem of the fuzzy control in the application of armed robot weapons platform stability control was proposed.Based on the analysis of the kinetics of stabilized platform in the past，we set up the input and output variables for the two-degree-of-freedom turntables，and ADAMS was employed to establish the mathematical model for the turntables.The turntables model established in ADAMS were imported to Matlab and the fuzzy controller was designed according to the dynamics of stabilized platform，and the block diagram for the fuzzy control system of the two-degree-of-freedom turntables was established through Matlab/Simulink.Through the simulation calculation，we analyzed the response characteristics of stabilized platform which under the effect of step torque signal and improved the control system.Finally we gave the results of ADAMS and Matlab joint simulation about the optimized control system.The results of the united simulation of Matlab and ADAMS show that the fuzzy controller designed in this paper has great effect in the armed robot weapons platform stability control.

stable platform；fuzzy control；united simulation

孙钟阜.模糊控制在武装机器人稳定平台中的应用［J］.四川兵工学报，2015（11）：15-18.

format：SUN Zhong-fu.Application of Fuzzy Control on Armed Robot's Turntable［J］.Journal of Sichuan Ordnance，2015（11）：15-18.

TP242；TJ9

A

1006-0707（2015）11-0015-04

10.11809/scbgxb2015.11.005

2015-05-25

孙钟阜（1965—），男，高级工程师，主要从事水声对抗，控制技术研究。