组合形变对三角形脊波导传输特性的影响

陈小强,杨立坤

(兰州交通大学自动化与电气工程学院,甘肃 兰州 730070)



·光纤及光通讯技术·

组合形变对三角形脊波导传输特性的影响

陈小强,杨立坤

(兰州交通大学自动化与电气工程学院,甘肃 兰州 730070)

脊波导的传输特性包括截止波长、单模带宽、衰减常数、功率容量以及特性阻抗。脊波导器件在装配使用中所产生的错位形变与边侧形变很难单独发生,因此,有必要研究错位形变、底部形变、单侧形变、双侧形变结合的组合形变。利用ANSYS建立模型与MATLAB编写有限元程序相结合的方法计算了三角形脊波导组合形变对其传输特性的影响。研究结果表明,组合形变对三角形脊波导的截止波长、单模带宽影响较小,三边形变与错位底部形变对三角形单脊波导功率容量、衰减常数及特性阻抗影响较大,研究结果将为三角形脊波导的应用提供了理论依据。

三角形脊波导；传输特性；组合形变

1 引 言

自1976年Konishi[1]把矩形脊波导制作为12 GHz低噪声变频器等器件应用于卫星通信后,脊波导倍受学者关注。1998年,J.Helszajn[2]首次提出梯形脊波导,并研究其阻抗特性。2000年,Yu Rong[3]计算了矩形脊波导的衰减常数与功率容量。2004年,M.Lu[4]利用有限元法计算了梯形脊波导的截至波长以及单模带宽。2007年，陈小强等[5]提出了三角形脊波导和倒梯形脊波导,并计算其单模带宽和截止波长。2008年,赵霞等[6]分析了不同形变对梯形脊波导的截止波长及单模带宽的影响。2011年,赵霞等[7]计算了形变对矩形脊波导的截止波长、单模带宽以及场分布的影响。2012年,李向葵等[8]计算了形变对梯形单脊波导衰减特性、功率容量及特性阻抗的影响,同年,陈彩虹等[9]分析了在不同形变下矩形单脊波导功率容量、衰减常数以及特性阻抗的变化趋势。由于脊波导器件在实际加工中,形变常常同时发生,以及加工成型的卫星天线系统,在太空中展开也可能造成器件形变,分析不同形变对器件特性的影响,有助于在薄弱结构上加强结构强度,减少变形对系统特性的影响。本文分析错位形变和侧边形变同时发生所引起的三角形脊波导传输特性的变化。

2 基本理论

假设脊波导内部为纵向均匀的空气介质,脊波导内部的纵向场结构可以归纳为Helmholtz方程:

(1)

式中,k为波数。利用有限元法[10]可以推导出脊波导的本征值矩阵方程:

(2)

矩阵A、B为N×N阶矩阵，通过式(2)求得脊波导的截止波数kc和截止频率fc(截止波长λc=2π/fc)。由主模截止波长λc以及第一次高次模截止波长λc1的比值计算单模带宽，即BW=λc/λc1。

(3)

其中，ω为角频率;μ为媒质磁导率;β为相位常数。

2.1 衰减常数及功率容量

在有损波导中，存在传输功率P=P0e-2αz，其中，P0为z=0处的传输功率，α为衰减常数。由于α远远小于1，存在P≈P0。α是由导体损耗αc以及介质损耗αd组成，本文所填充的介质为空气，其介质损耗远小于导体损耗，故α=αc。

(4)

其中，Rs为表面电阻，将式(3)代入式(4)得：

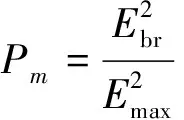
2.2 特性阻抗

脊波导任意频率下的特性阻抗为:

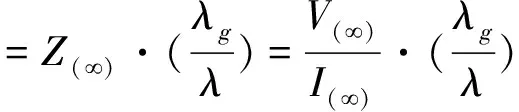
其中,Z()为频率无限大时的特性阻抗;λ为工作波长;V()和V(ωc)分别表示频率无限大以及截止频率时的脊波导中心电压总和;I()和I(ωc)分别表示频率无限大以及截止频率时的脊波导波导壁电流总和。

就三角形单脊波导而言:

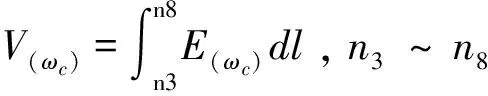
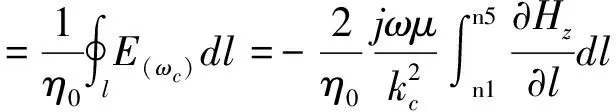
其中，η0为自由空间波阻抗。如图1所示，图1(a)表示三角形单脊波导错位形变与单侧形变组合，图1(b)、(c)、(d)分别表示三角形单脊波导错位形变与双侧形变的组合，错位形变与底部形变的组合以及三边形变；图1(e)、(f)分别表示三角形双脊波导错位形变与单侧、双侧形变的组合。

图1 各种组合形变三角形脊波导的横截面图

3 数值计算结果

3.1 脊波导尺寸选择

为了方便对比,三角形单脊双脊波导均选用b/a=0.45,s/a=0.4,d/b=0.4的形状比例。在形变时,形变量不超过宽边的10%,即σ10%。

3.2 计算结果

3.2.1 三角形单脊波导

图2为三角形单脊波导传输特性的各项参数(即截止波长、单模带宽、功率容量、衰减常数及特性阻抗)随形变量增加而变化的曲线图。

图2 三角形单脊波导形变特性参数变化曲线图

3.2.2 三角形双脊波导

图3为三角形双脊波导的传输特性参数随形变量增加而变化的曲线图。

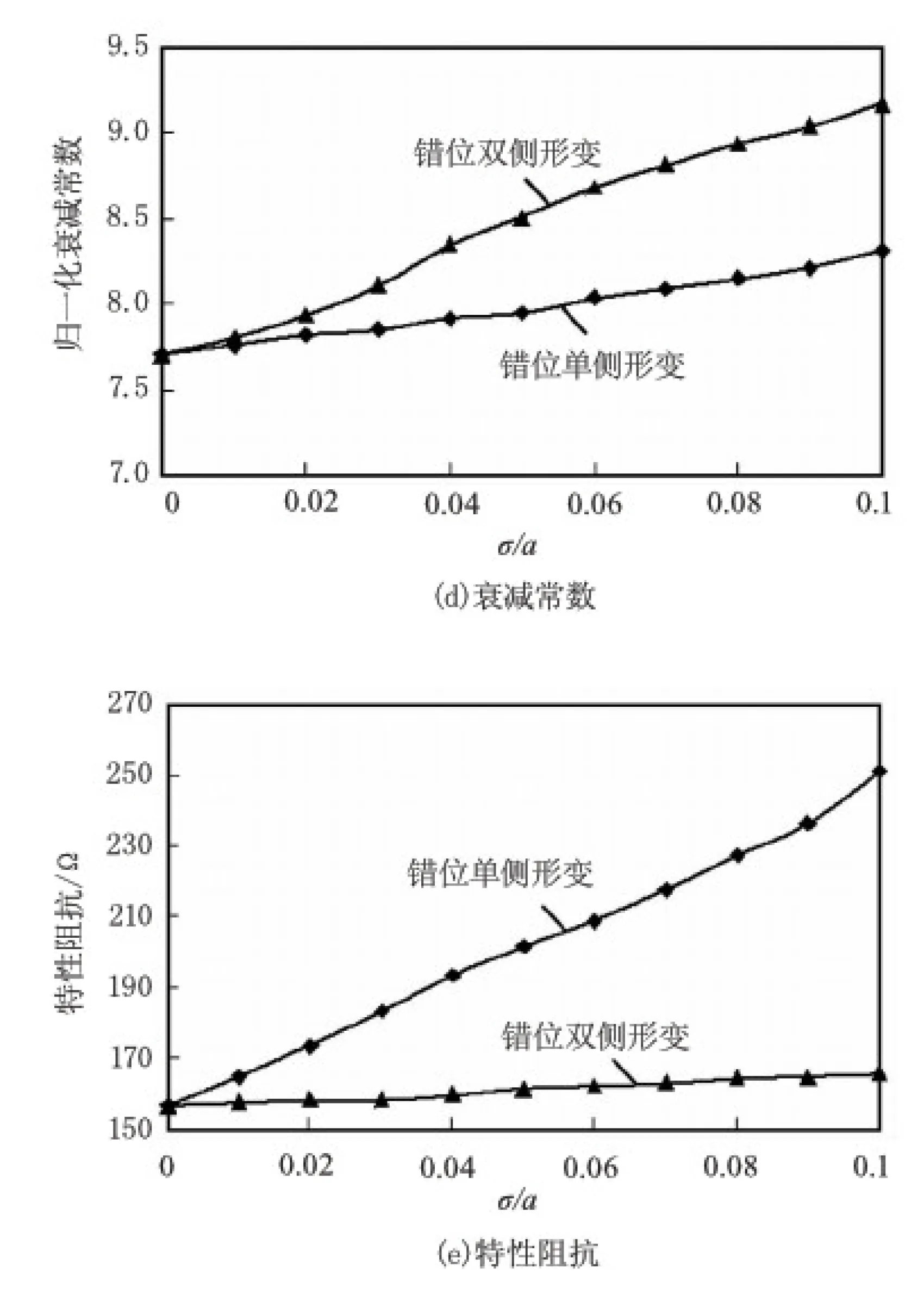
图3 三角形双脊波导形变特性参数变化曲线图

3.3 结果分析

本文利用ANSYS建立模型,在MATLAB下编写程序计算的方法研究错位和边侧形变同时发生时三角形脊波导传输特性的变化,并绘制出参数变化曲线图。定义形变引起的参数变化率=|形变参数-未形变参数|/未形变参数×100%。对计算结果分析如下:

(1)错位单侧形变与错位双侧形变对三角形单脊、双脊波导传输特性影响的变化规律相似,随着形变量(不超过10%)的增加,三角形脊波导的截止波长、单模带宽、功率容量均减小,衰减常数以及特性阻抗增大。

(2)三边形变与错位底边形变对三角形单脊波导的传输特性影响的变化规律相似,随着形变量(不超过10%)的增加,截止波长、单模带宽及衰减常数增大,功率容量与特性阻抗减小。

(3)对于三角形单脊波导而言,错位底部形变对截止波长、单模带宽、功率容量及衰减常数影响最大,当形变达到10%时,各参数的变化率分别为15.98%、23.36%、49.68%、51.99%；三边形变对特性阻抗影响最大,形变达到10%时,变化率为36.16%。

(4)对于三角形双脊波导而言,错位双侧形变对截止波长及单模带宽的影响约为错位单侧性变的2倍；当形变量超过5%时,单模带宽的变化率增大；错位单侧形变对功率容量与阻抗特性影响较大,形变达到10%时,变化率分别为63.79%和60.47%；错位双侧形变对衰减常数的影响较大,形变达到10%时,变化率为19.10%。

4 结 论

组合形变对三角形脊波导截止波长与单模带宽影响较小,错位底部形变与三边形变对三边形单脊波导功率容量、衰减常数以及特性阻抗影响较大,应尽量避免。在不同的工程应用中所需的传输特性不同,应综合考虑各项参数的变化。这些数据将为三角形脊波导的应用提供理论基础。

[1] Y Konishi,H Matsumura.Short end effect of ridge guide with planar circuit in a mounted waveguide [J].IEEE Trans.Microwave Theory Tech,1979,27(2):168-170.

[2] J Helszajn,M McKay.Voltage-current definition of impendence of double ridge waveguide using the finite element method[J].IEEE Proc.Microw.Antennas Propag,1998,145(1):39-44.

[3] Yu Rong,Kawthar A.Zaki.Characteristics of Generalized Rectangular and Circular Ridge Wavguides[J].IEEE Transactions on Microwave Theory and Techniques,2000,48(2):258-265.

[4] M Lu,P J Leonard.Design of trapezoidal-ridge wavegu-ide by finite element method[J].IEEE Proc.Microw.Ante-nnas Propag,2004,151(3):205-211.

[5] CHEN X Q,LI M,REN E E.Study of transmission characteristics of two kinds of new double-ridge waveguide[J].Journal of Xidian University,2007,34(3):495-499.(in Chinese)

陈小强,李明,任恩恩,等.两种新型双脊波导传输特性的研究[J].西安电子科技大学学报,2007,34(3):495-499.

[6] ZHAO X,CHEN X Q.Study of Transmission Characteristic of Trapezoidal-ridge Waveguide in Different Distortions[J].Laser & Infrared,2008,38(6):590-592.(in Chinese)

赵霞,陈小强,等.不同变形下梯形脊波导传输特性研究[J].激光与红外,2008,38(6):590-592.

[7] ZHAO X,CHEN X Q.Analysis on Transmission Characteristics of Rectangular-ridge Waveguide in Deformation[J].Radio Engineering,2011,41(1):35-37.(in Chinese)

赵霞,陈小强.变形矩形脊波导传输特性分析[J].无线电工程,2011,41(1):35-37.

[8] LI X K,CHEN X Q,CHEN C H.Attenuation transmission characteristics of trapezoidal single-ridge waveguide in deformations[J].Journal of Lanzhou University:Natural Sciences,2012,48(5):124-128.(in Chinese)

李向葵,陈小强,陈彩红.变形对梯形单脊波导衰减等传输特性影响[J].兰州大学学报:自然科学版,2012,48(5):124-128.

[9] CHEN C H,CHEN X Q.Effects of deformations on characteristics of rectangular single-ridge Waveguide[J].Study on Optical Communication,2012,(4):52-55.(in Chinese)

陈彩红,陈小强.变形对矩形单脊波导特性的影响[J].光通信研究,2012,(4):52-55.

[10]JIN J M.Finite Element Method for Electromagnetic Field[M].Xi′an:Press of Xidian University,2001.(in Chinese)

金建铭.电磁场有限方法[M].西安:西安电子科技大学出版社,2001.

Transmission characteristics of triangle ridge waveguide in combined deformations

CHEN Xiao-qiang，YANG Li-kun

(School of Automation and Electrical Engineering,Lanzhou Jiaotong University,Lanzhou 730070,China)

The transmission characteristics of ridge waveguide include cutoff wavelength,single-mode bandwidth,attenuation constant,power handling capacity and characteristic impedance.In implementation,displacement deformation and side deformation is difficult to generate alone in the ridge waveguide.Therefore,the combination of displacement deformation,bottom deformation,unilateral and bilateral deformation needs to be studied.Influence of the combined deformation of triangle ridge waveguides on the transmission characteristics is calculated using ANSYS to establish model and MATLAB to write finite element program.Calculation results demonstrate that combined deformation has smaller influence on the cutoff wavelength and single-mode bandwidth of triangle ridge waveguide,while trilateral deformation and displacement bottom deformation have greater influence on the attenuation constant,power handling capacity,and characteristic impedance of triangle ridge waveguide.The research results will provide a theoretical foundation for the application of triangle ridge waveguide.

triangle ridge waveguide;transmission characteristics;combined deformations

1001-5078(2015)10-1244-05

甘肃省科技计划项目(No.145RJZA098);铁道部科技研究开发计划课题项目(No.2011X008-D)资助。

陈小强(1966-),教授,主要研究方向为电磁场与微波技术,计算电磁学。

杨立坤(1991-),硕士生,主要研究方向为电磁场与微波技术。E-mail:yanglikun0221@foxmail.com

2014-01-21;

2015-03-13

TP391.41

A

10.3969/j.issn.1001-5078.2015.10.020