铁氧体同轴传输线脉冲锐化特性的研究
2015-11-25乔中兴
乔中兴 刘 恺 董 寅
(浙江工业大学光纤通信研究所 杭州 310013)
0 引言
近来,用于压缩脉冲前沿上升时间的铁氧体非线性传输线倍受关注。火花隙或脉冲闸流管等设备都可以产生脉冲上升时间小于200ps 的快脉冲,但其重复频率限制于1kHz 左右[1],且在高要求的情况下存在一定缺陷(如火花隙的触发不稳定,闸流管的导通时间长等[2])。而铁氧体非线性同轴传输线可以在高电压环境中工作,具有良好的重频特性和寿命。尽管存在缺点,如因脉冲损耗而降低了电路效率,但其仍是该领域为数不多可选的技术之一[3]。另一方面,铁氧体传输线还可作为高功率微波源,其可以产生频率为数GHz,功率高达MW 级的微波[4-6]。相较其他高功率微波源,铁氧体传输线的结构简单,设备规模也较小,完全可以取代电子束、真空管等传统的高功率微波源[7]。因此铁氧体传输线在激光束武器、超宽带无线通信(Ultra Wideband,UWB)和大功率通信设备中有着很广泛的应用前景。
铁氧体传输线的一个作用是将输入脉冲的前沿锐化。仿真结果表明,铁氧体传输线可以有效地压缩脉冲前沿的上升时间。本文首先介绍国内外在此领域的研究现状;然后阐述脉冲锐化机制与非线性铁氧体传输线的特性;接着利用仿真软件COMSOL Multiphysics 建立模型进行仿真,得到铁氧体传输线锐化效果与脉冲电压幅值、传输线半径相关的工作特性;最后根据仿真结果进行研究探讨。
1 国内外研究现状
铁氧体同轴传输线脉冲锐化特性的研究由来已久,文献[8]中首先提出了使用非线性传输线来锐化脉冲的理论解释,并通过建立一系列的数学模型来进行描述。文献[9]将锐化原因归结于铁氧体的旋磁进动行为,并得到了电压幅值20kV,上升时间60ps的快脉冲。文献[3]以波前能量耗散的方式来解释脉冲锐化的原因,制作了长度120cm,同轴线内外半径分别为0.64cm 和0.24cm,单个磁心长度1.25cm,内外半径分别为0.25cm 和0.5cm 的传输线用于实验,并在不同的输入脉冲电压幅值、铁氧体磁心长度以及附加偏置磁场的情况下进行对比实验,发现在附加偏置磁场为零的情况下,脉冲锐化效应仍然存在。文献[10]将一维TEM 传输线模型和LLG 方程结合进行模拟分析,得出入射脉冲电压越大,锐化效果越好的结论。与此同时,对于相同尺寸传输线来说,铁氧体较高的饱和磁感应强度可以得到更短的脉冲前沿上升时间。文献[11]在输入100kV,上升时间为1.6ns 的脉冲电压情况下,获得了输出电压为90kV,脉冲前沿上升时间锐化至85ps 的电磁冲击波。对于国内,文献[12]设计了一种同时接两根铁氧体线的双线发生器,获得了脉冲前沿锐化至2ns 左右,脉冲重复频率10Hz、50Hz、300Hz可调的效果。文献[2]也设计了铁氧体传输线用于实验,获得了电压幅值3~7kV,前沿1~2ns 的高重频脉冲。如何对铁氧体传输线进行优化,设计出一个高效低能耗的传输线是今后需要研究的问题。
2 传输线工作原理
2.1 脉冲锐化机制
铁氧体材料的磁导率与磁化强度之间有着高度的非线性关系,脉冲锐化效果正是基于此才得以实现。在一般情况下,铁氧体的相对磁导率是相当大的,但在强磁场下磁导率会迅速减小。也就是说,足够大的磁场强度能使铁氧体材料达到饱和状态,使其相对磁导率的值减小到个位数[13],约为3 或1。
波的传播速度方程为[14]

式中,ε 为介质的介电常数(F/m), ε=ε0εr;μ 为介质磁导率(H/m), μ=μ0μr。
根据式(1)中所呈现的反比关系,铁氧体相对磁导率的变化直接影响了脉冲前沿传播相速度的变化。随着高电压脉冲沿着传输线传播,电压幅度逐渐增加,铁氧体也随之逐渐励磁,使得磁导率降低,波速增快。于是在铁氧体传输线中,脉冲前沿的每一个断面都有着自己的传播速度[2],其在传播过程中不断“变形”,整体来看便有脉冲前沿的尾部“赶上了”脉冲前沿头部,使得脉冲前沿被压缩,实现锐化效果。当铁氧体全部达到饱和状态之后,脉冲前沿各点的波速便不会再发生变化。
2.2 传输线理论
填充铁氧体的同轴传输线结构如图1 所示。
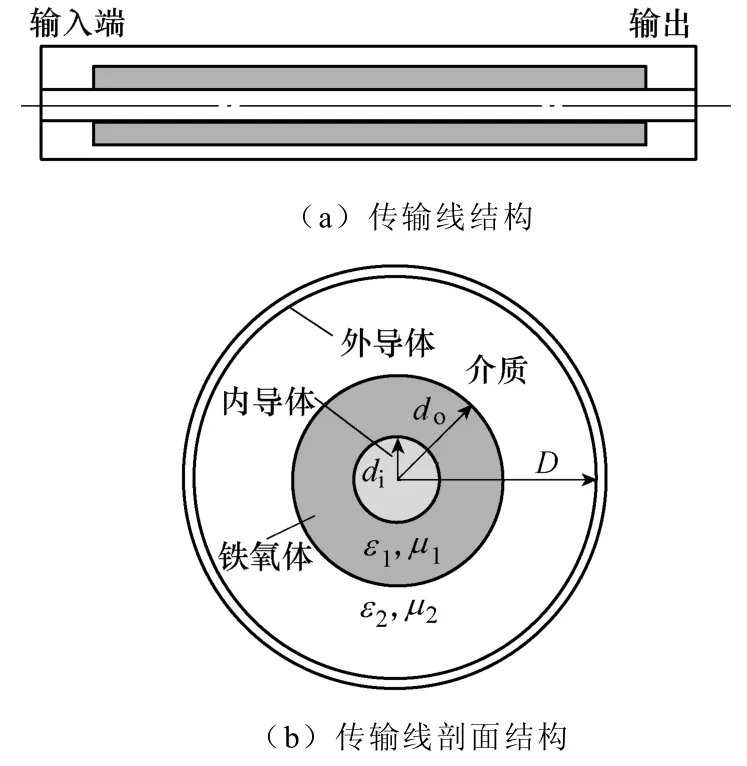
图1 铁氧体填充同轴传输线结构及其横截面Fig.1 Structure and cross-section view of the ferrite-filled transmission line
忽略铁氧体与介质之间的空隙,传输线单位长度电容和电感为
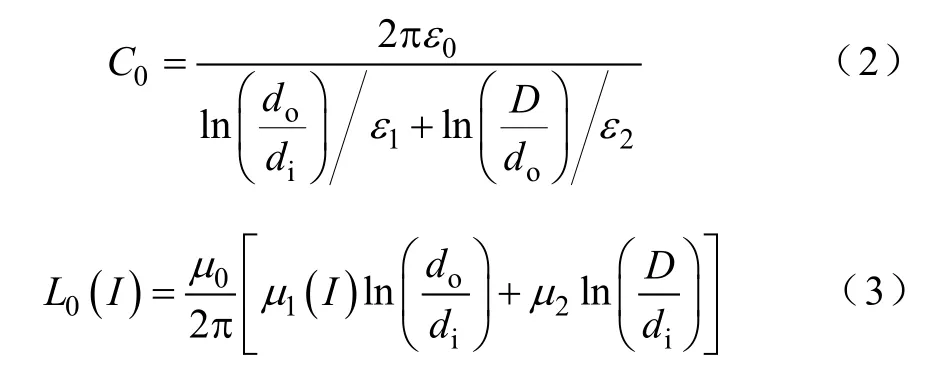
在式(3)中,铁氧体相对磁导率是关于电流的函数。传输线特征阻抗即为

传输线电感是关于材料磁导率的函数。在脉冲沿着传输线传播的过程中,铁氧体逐渐饱和,传输线的特征阻抗也会逐渐减小达到饱和值。

饱和状态下的特征阻抗 Z0s一般设计成50Ω,当然也可以是其他任意需要的特定值。这个值对建立仿真模型至关重要。为了减小微波形成过程中的反射,输出端负载阻抗必须要与饱和状态下的传输线阻抗相匹配。
另外,传输线电长度也是一个相当重要的参数,它决定了输入脉冲前沿的最大允许上升时间。

式中,length 为传输线长度;vp为传播速度。输入脉冲电压必须在到达输出端之前达到最大峰值,以便对电压幅值影响脉冲锐化效果的讨论能够更加准确。
由于在同轴线中一般传播的是TEM 模,其一维传输线方程可写成
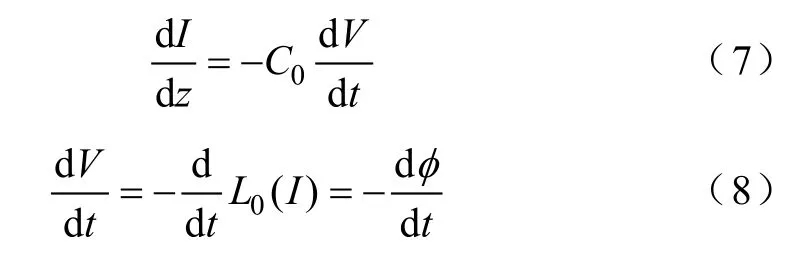
式中,L0(I)为随电流值变化的单位长度电感;φ 为单位长度磁通量(Wb)。
式(8)可分解成线性与非线性两个部分[15]
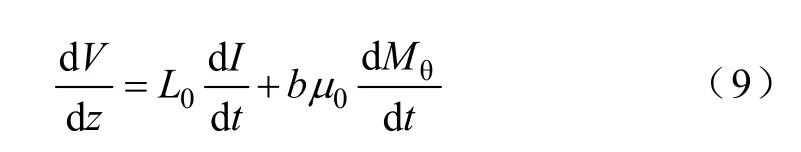
式中,b 为铁氧体的径向半径(m);dMθdt 为磁矩圆周分量随时间的变化量。由此可见,铁氧体径向半径变量b 也影响着脉冲前沿的“形变”。
3 仿真
本实验使用软件COMSOL Multiphysics 中的RF 模块进行仿真。铁氧体内外半径分别为3mm 和6.4mm。尺寸规格见表1。材料的非线性磁导率函数由图2 定义。输入端与输出端的负载阻抗设置成50Ω以匹配传输线阻抗,并在传输线的两个端口设置探针对脉冲波形进行监测。
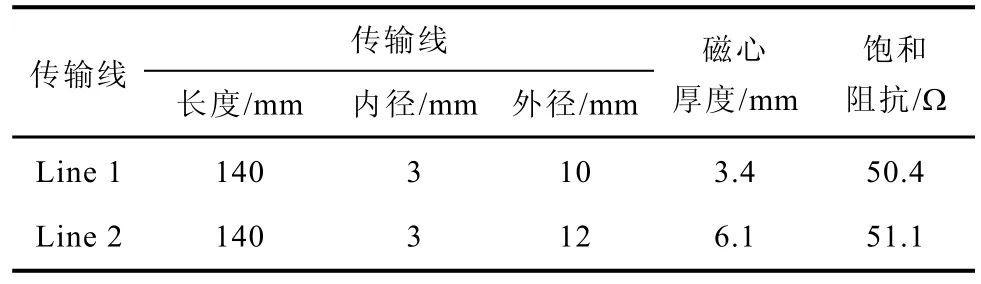
表1 铁氧体传输线尺寸规格Tab.1 The size of ferrite-filled transmission line
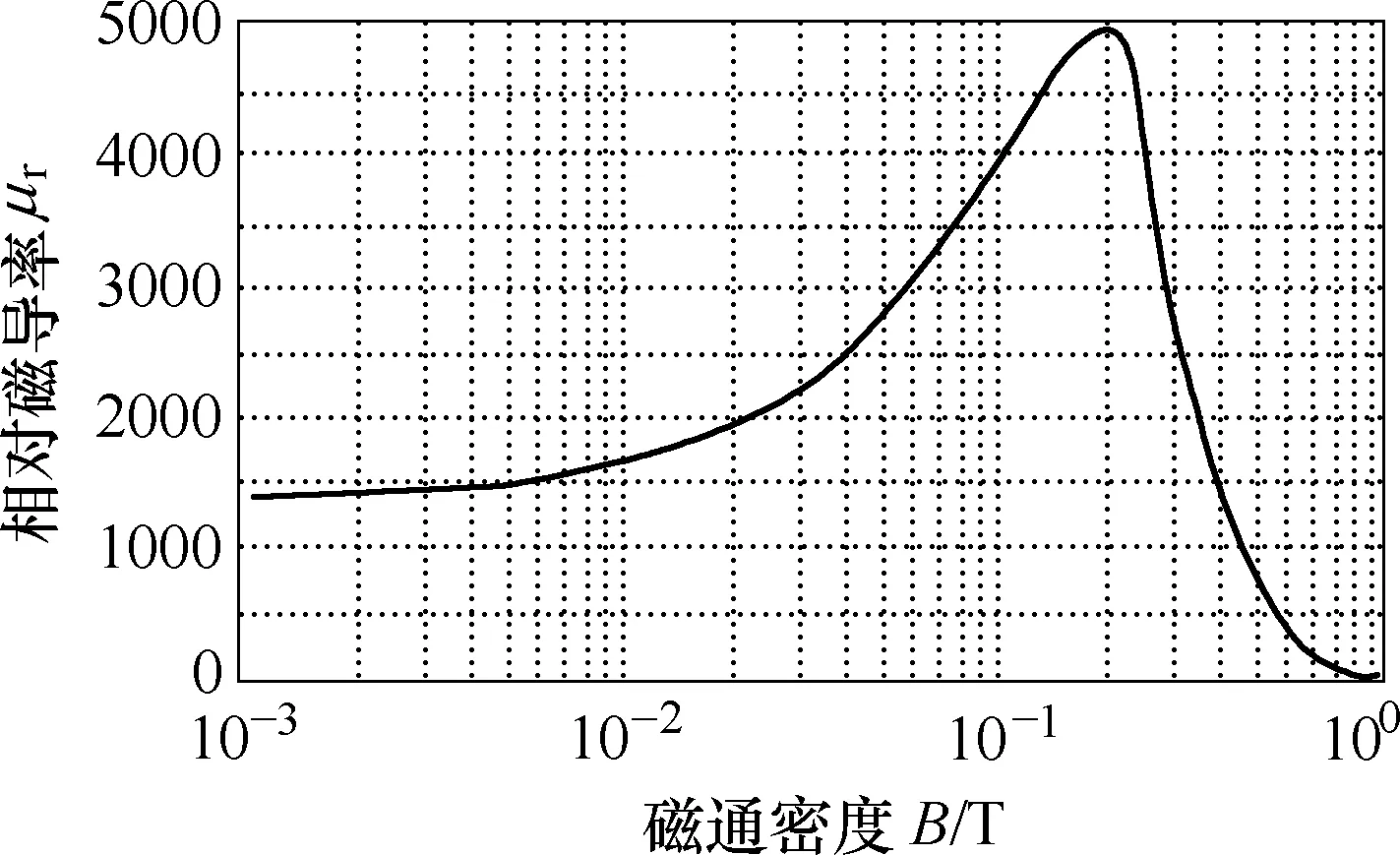
图2 铁氧体相对磁导率与磁通密度关系函数Fig.2 The function of the relative permeability versus magnetic flux density for the simulated ferrite material
脉冲锐化过程中,铁氧体材料在不同时刻相对磁导率的变化如图3 所示。自旋饱和前端[3]沿着铁氧体材料传播,将饱和区域留在后面。在饱和区域中脉冲前沿“尾部”的传播速度比不饱和区域中的脉冲前沿“头部”要快得多,以此完成脉冲前沿锐化过程。
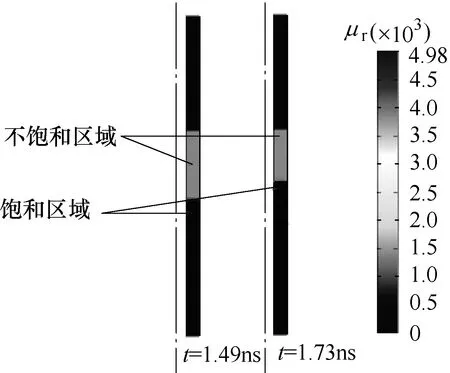
图3 铁氧体不同时刻相对磁导率的对比Fig.3 The comparison of the relative permeability at two different times

图4 50kV 脉冲仿真波形Fig.4 The simulation waveforms of a 50kV input pulse
图4 为铁氧体传输线仿真的锐化效果示例。脉冲源设置成阶跃函数,电压幅值50kV,脉冲前沿上升时间为1.6ns。传输线输入端的电压波形在一段时间内存在相当大的反射,电压值远大于脉冲源的峰值电压。直至铁氧体逐渐饱和,传输线阻抗与两端负载阻抗相匹配,输入端电压值才下降至50kV。输出端波形在脉冲前沿完全通过铁氧体材料之前都相对平坦,直至某一时刻电压值突然上升,脉冲锐化的效果十分明显。
在模型仿真过程中,输入脉冲电压幅值对锐化效果影响最直观。足够高的电压能使铁氧体逐步励磁并达到饱和状态,使得输出脉冲的上升时间明显减少。然而,若输入脉冲的电压值过小而不足以驱动铁氧体饱和,反而将对脉冲锐化起到反作用。如图5 所示,输入脉冲前沿的上升时间为1.6ns,对于当前尺寸的传输线,输入电压至少要4kV 才能获得锐化效果。脉冲电压的逐渐增大可以有效地减少输出脉冲前沿的上升时间。
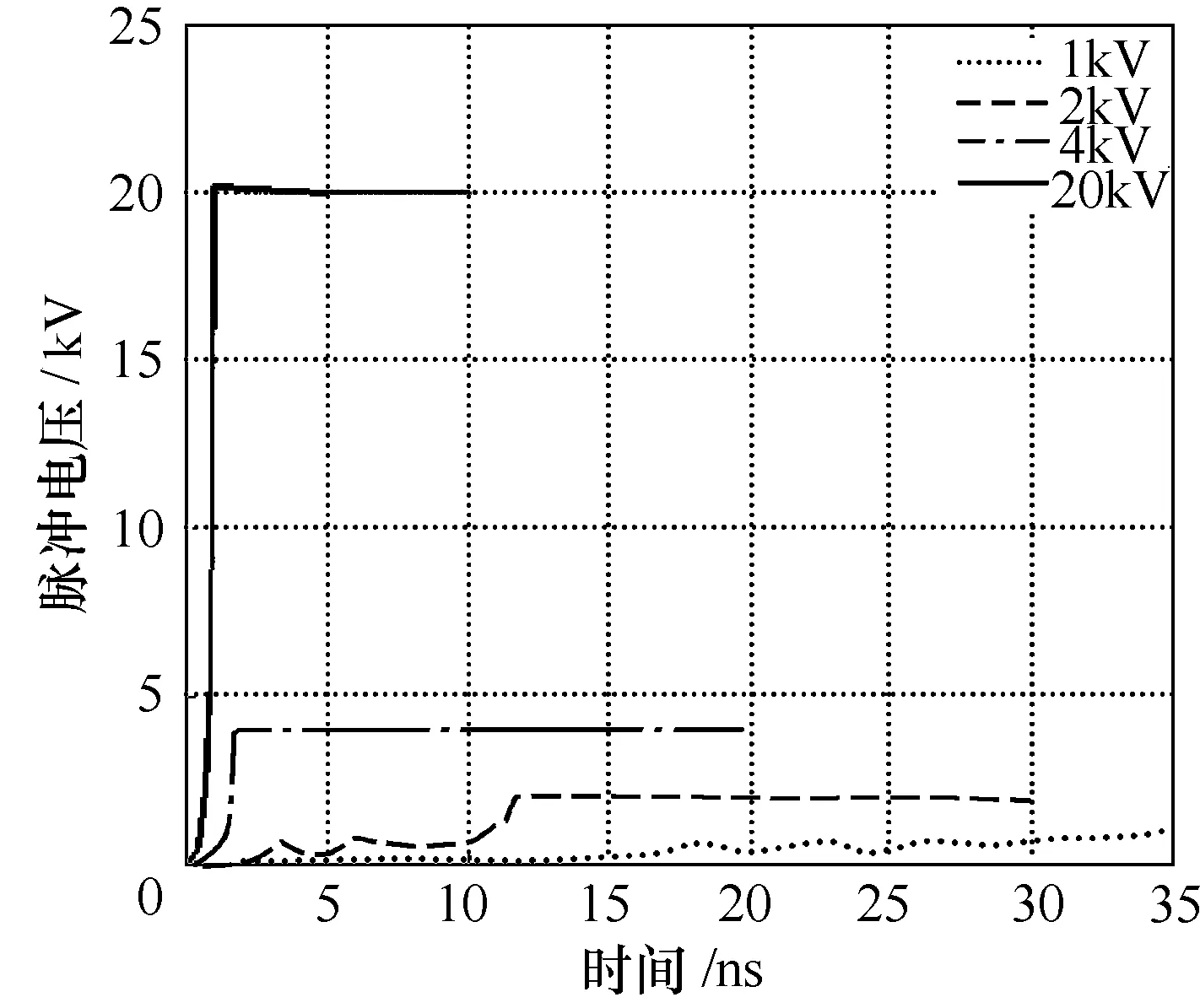
图5 Line 1 不同输入电压所产生的输出电压波形Fig.5 Output waveforms of Line 1 for different incident voltages
为了研究传输线中铁氧体径向半径对能起到锐化脉冲效果的最低输入电压幅值的影响,建立了一个半径不同的模型。Line 2 传输线模型的长度不变,同样为140mm,而内、外半径则分别设置成3mm和12mm,内部填充的铁氧体的内、外半径分别为3mm 和9.1mm,使其饱和阻抗保持为50Ω左右。输出仿真波形如图6 所示。在输入脉冲电压幅值达到6kV 时,锐化效果才足够明显。由此可见,铁氧体径向半径在一定程度上影响了脉冲前沿传播过程的“形变”。半径较大的传输线由于在径向截面上包含了更多的铁氧体,需要更高的输入电压来驱动铁氧体达到饱和状态,实现锐化效果。
4 结论
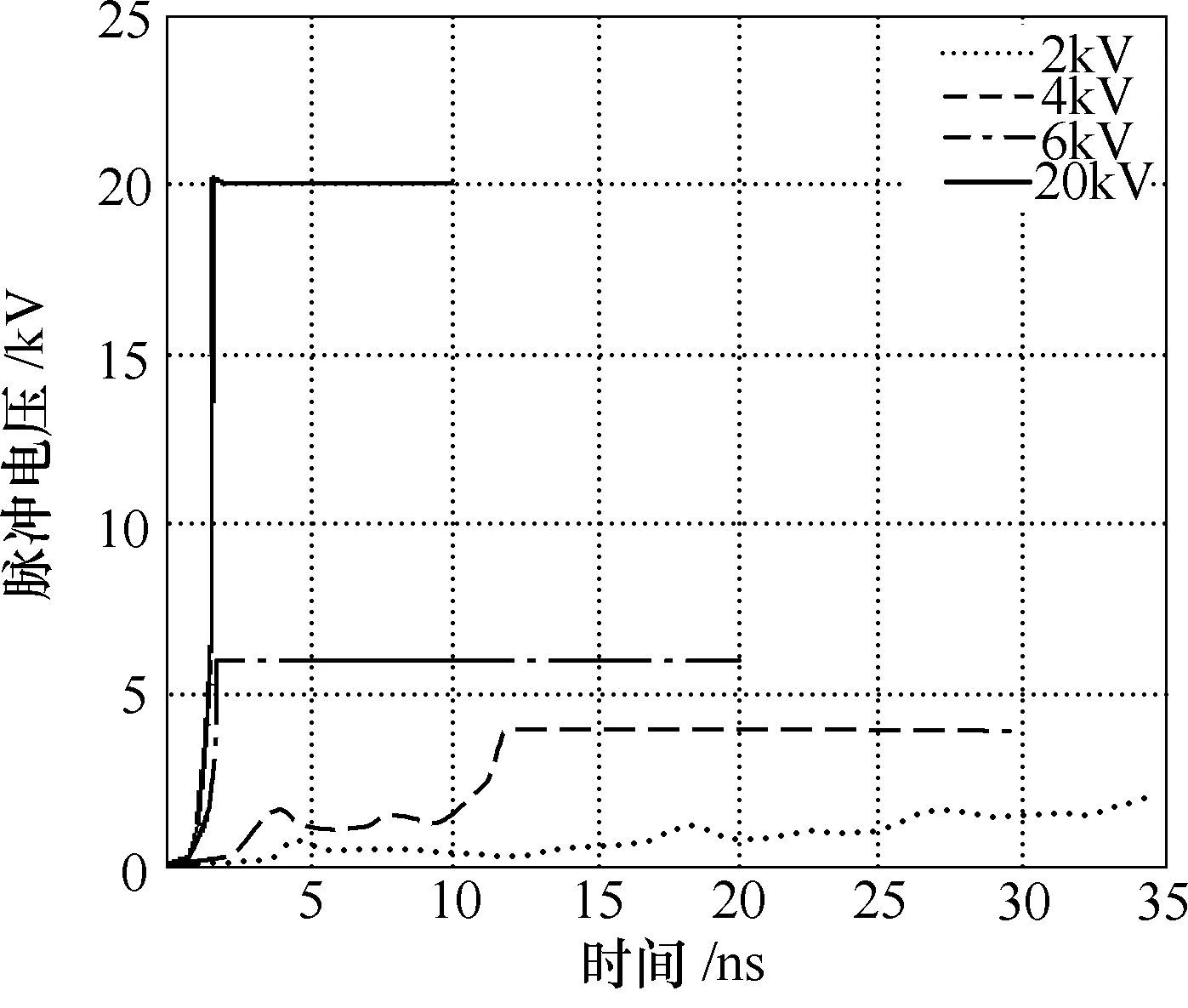
图6 Line 2 不同输入电压产生的输出电压波形Fig.6 Output waveforms of Line 2 for different incident voltages
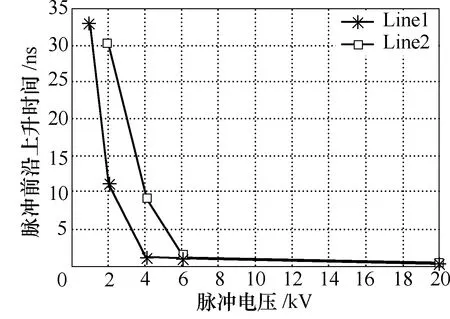
图7 两条传输线不同输入电压幅值对应的输出脉冲前沿上升时间Fig.7 Rise times versus the different voltage for the two transmission lines
铁氧体同轴传输线为压缩脉冲前沿的上升时间提供了一种有效的方法。本文首先讨论了电压幅值对锐化效果的影响,逐渐增大输入脉冲的电压峰值确实可以使锐化效果更加明显。与此同时,铁氧体径向半径的变化对最低输入电压幅值的影响也十分明显。对于较大半径的传输线,输入脉冲需要更大的电压值来使传输线实现脉冲锐化的效果。这将为制备铁氧体传输线的实物模型提供设计参考。
[1]Frost C A,Martin T H,Patterson P E,et al.Ultrafast gas switching experiments[R].Sandia National Labs,Albuquerque,NM (United States).Funding organization:USDOE,Washington,DC (United States),1993.
[2]镡延桢,王明宝.铁氧体同轴线的特性及其应用[J].光纤与电缆及其应用技术,1980(5):2.
[3]Weiner M,Silber L.Pulse sharpening effects in ferrites[J].IEEE Transactions on Magnetics,1981,17(4):1472-1477.
[4]Bragg J B,Dickens J C,Neuber A A.Ferromagnetic nonlinear transmission lines as high-power microwave sources[J].IEEE Transactions on Plasma Science,2013,41(1):232-237.
[5]Bragg J,Dickens J,Neuber A.Magnetic biasing of ferrite filled nonlinear transmission lines[C]//2010 IEEE International Power Modulator and High Voltage Conference (IPMHVC),Atlanta,GA,2010:600-603.
[6]Reale D V,Bragg J W B,Holt S L,et al.Bias field controlled phasing of ferrimagnetic coaxial nonlinear transmission lines[C]//2013 19th IEEE Pulsed Power Conference (PPC),San Francisco,CA,2013:1-3.
[7]Sanders J M,Lin Y H,Ness R,et al.Pulse sharpening and soliton generation with nonlinear transmission lines for producing RF bursts[C]//2010 IEEE International Power Modulator and High Voltage Conference (IPMHVC),Atlanta,GA,2010:604-607.
[8]Gaponov A V,Ostrovskii L A,Freidman G I.Electromagnetic shock waves[J].Radiophysics and Quantum Electronics,1967,10(9):772-793.
[9]Dolan J E,Bolton H R,Shapland A J.Development of 60ps rise-time ferrite-loaded coaxial line[J].Electronics Letters,1997,33(24):2049-2050.
[10]Dolan J E,Bolton H R.Shock front development in ferrite-loaded coaxial lines with axial bias[J].IEE Proceedings of Science,Measurement and Technology,2000,147(5):237-242.
[11]Brooker C,Altieri N,Eastwood G,et al.90kV 1800A 85ps rise time electromagnetic shock line for UWB applications[J].Electronics Letters,1999,35(25):2210-2212.
[12]陈家因,管革新,杨真媛.强功率铁氧体线短脉冲的产生[J].原子能科学技术,1986(6):7.
[13]Sullivan I W,Dickens J,Kristiansen M.Shock wave simulation of ferrite-filled coaxial nonlinear transmission lines[C]//Proceedings of the 2008 IEEE International Power Modulators and High Voltage Conference,Las Vegas,NE,2008:517-520.
[14]Gaponov A V,Ostrovskii L A,Freidman G I.Electromagnetic shock waves[J].Radiophysics &Quantum Electronics,1967,10(9):772-793.
[15]Dolan J E.Simulation of ferrite-loaded coaxial lines[J].Electronics Letters,1993,29(9):762-763.
