长大连续坡道梯形轨道垂向动力学性能研究

李 娟,刘学毅,刘 欢,袁岳淦

(1.西南交通大学高速铁路线路工程教育部重点实验室,成都 610031；2.广州铁路股份有限公司广州工务段,广州 510610)

长大连续坡道梯形轨道垂向动力学性能研究

李 娟1,刘学毅1,刘 欢1,袁岳淦2

(1.西南交通大学高速铁路线路工程教育部重点实验室,成都 610031；2.广州铁路股份有限公司广州工务段,广州 510610)

梯形轨枕轨道是一种纵向轨枕轨道系统,轨枕由 PC纵梁和横向钢管联接杆件构成。国内外城市轨道系统铺设梯形轨道的应用结果表明,梯形轨枕可大幅度提高对列车荷重的分散能力,且具有良好的减振和降噪性能。根据梯形轨枕轨道结构特点建立弹性地基梁-板模型,利用有限元方法计算在不同列车运行速度和不同坡度情况下梯形轨枕轨道系统的垂向动力响应,对在线路长、落差高的长大连续坡道上铺设梯形轨道的垂向稳定性进行论证。计算结果表明长大连续坡道上梯形轨枕垂向动力响应符合标准,可以在城市轨道交通的长大连续坡道区段铺设。

长大连续坡道；梯形轨枕；有限元方法；垂向动力响应

图1 梯形轨枕

梯形轨枕轨道主要由钢轨、扣件、梯形轨枕、减振垫、缓冲材料以及L形混凝土支座构成。梯形轨枕是一种纵向轨枕，轨枕由 PC纵梁和横向钢管连接杆构成，如图1所示。PC纵梁起到在钢轨之外的第二纵梁的作用，钢轨和PC纵梁共同承载列车荷重，起到了轨道刚性较大的“复合轨道”的作用，提高了轨道的分散动荷载性能[1-2]。利用减振材料等间隔支撑结构，使轨枕浮置于混凝土整体道床上，可实现轻型无砟轨道构想，达到减少支撑方便维修的目的，同时，在很大程度减小了结构噪声，成为一种低噪声、低振动的轨道构造[2-3]。

但在长大连续坡道线路地段，梯形轨枕因承受较大的坡道纵向分力，可能存在轨道稳定性问题。某城市轨道交通线某区段线路存在长大坡道地段，下坡线路长度达到12 km，最大高差达200 m以上，线路大部分的坡度在20‰以上，有一半的线路坡度为28‰。根据该连续长大坡道线路长、高落差的特点，建立长大连续坡道上梯形轨道系统的动力学计算模型，在不同的列车运行速度和不同坡度下，研究轨道系统的动力性能，对长大连续坡道上铺设梯形轨道的可行性进行论证。

1 车辆-梯形轨道-路基垂向耦合动力计算模型

根据列车轨道在大坡道上的受力特点，建立了车辆-梯形轨道-路基垂向耦合动力计算模型，模型由车辆模型、梯形轨枕轨道模型、路基组成，如图2所示，并考虑坡道分力和轨道不平顺作为系统的激励。

图2 车辆-梯形轨道-路基垂向耦合振动系统计算模型

车辆为地铁B型车，模型中车辆系统采用全车模型，车辆模型是由车体、转向架、轮对以及弹簧-阻尼器悬挂装置组成的多自由度振动系统。各刚体在空间具有浮、侧滚和点头3个自由度，刚体间通过一系、二系悬挂等弹性元件联接[4，8-10]。由于车辆运行速度较低，故计算中采用轨道不平顺谱为德国低速高干扰谱，且德国高速低干扰谱利用自编程序模拟产生。

梯形轨枕轨道系统主要由钢轨、扣件、梯形轨枕、减振垫、缓冲材料以及L形混凝土支座构成，梯形轨枕设计的几何参数见图3，其他参数如表1中所列[4-7，11]。

梯形轨道结构各承载层在厚度方向的尺寸远小于在长度和宽度上的尺寸，且在荷载作用下的挠度远小于其厚度，符合弹性薄板的结构特点，适合于采用板壳理论模型，因此轨道采用弹性地基梁-板模型。轨道结构的支承考虑为弹性点支承，钢轨简化为欧拉梁模型，扣件简化为点支承线性弹簧，轨枕纵梁简化为弹性地基上的薄板，连接钢管、减振垫层简化为线性弹簧，路基简化为弹性面支承，轮轨接触考虑为赫兹线性弹簧接触[4-6]。运用有限元方法对列车动荷载下的梯形轨道系统垂向动力响应进行计算。

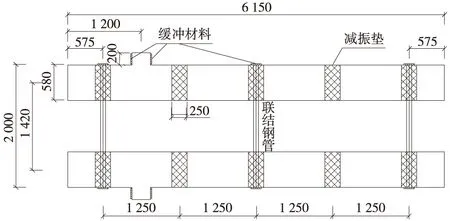
图3 梯形轨枕平面布置(单位：mm)

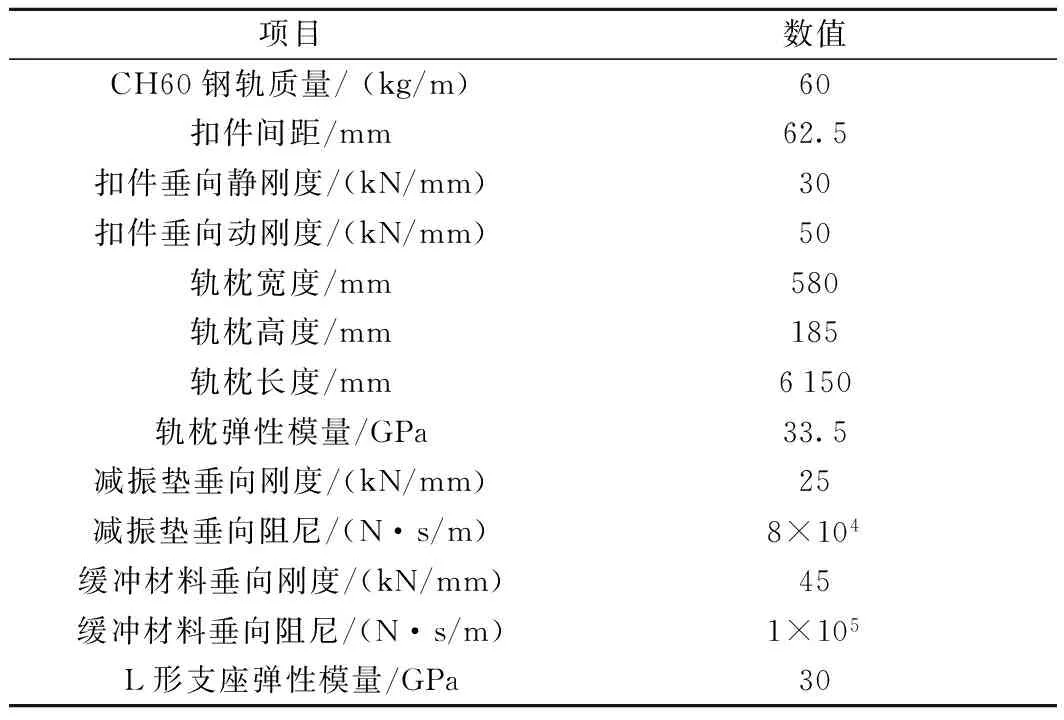
项目数值CH60钢轨质量/(kg/m)60扣件间距/mm62.5扣件垂向静刚度/(kN/mm)30扣件垂向动刚度/(kN/mm)50轨枕宽度/mm580轨枕高度/mm185轨枕长度/mm6150轨枕弹性模量/GPa33.5减振垫垂向刚度/(kN/mm)25减振垫垂向阻尼/(N·s/m)8×104缓冲材料垂向刚度/(kN/mm)45缓冲材料垂向阻尼/(N·s/m)1×105L形支座弹性模量/GPa30

在本文动力学模型中，梯形轨道计算模型为纵向水平无坡度模型，纵向长度112 m，共18块轨枕板，为消除边界效应，取模型中部位置处的动力响应作为计算结果，只考虑垂向振动，而不考虑横向和纵向振动的影响。运用有限元方法及Ansys/LSDYNA软件进行计算，研究坡度的影响时将荷载按照沿坡道纵向和垂直于坡道方向分解以模拟不同坡度。

2 梯形轨枕轨道系统垂向动力学性能计算结果分析

根据选定的梯形轨道结构参数，分析时采用单因子变量法，分别考虑车速和坡度的变化对结构垂向动力响应的影响，考虑工况如下。

线路纵向坡度：无坡度、28‰、35‰、40‰。

列车运行速度：90、120、140、160 km/h。

将轨道垂向位移、车体和轨道垂向振动加速度、轮轨垂向力、轮重减载率作为评价行车安全性的标准。

2.1 不同车速对车辆和轨道结构垂向动力响应的影响

当线路纵向坡度为0，而车辆行驶速度分别为90、120、140、160 km/h时，对梯形轨枕轨道结构的垂向动力响应进行分析，得到计算结果如图4和表2所示。

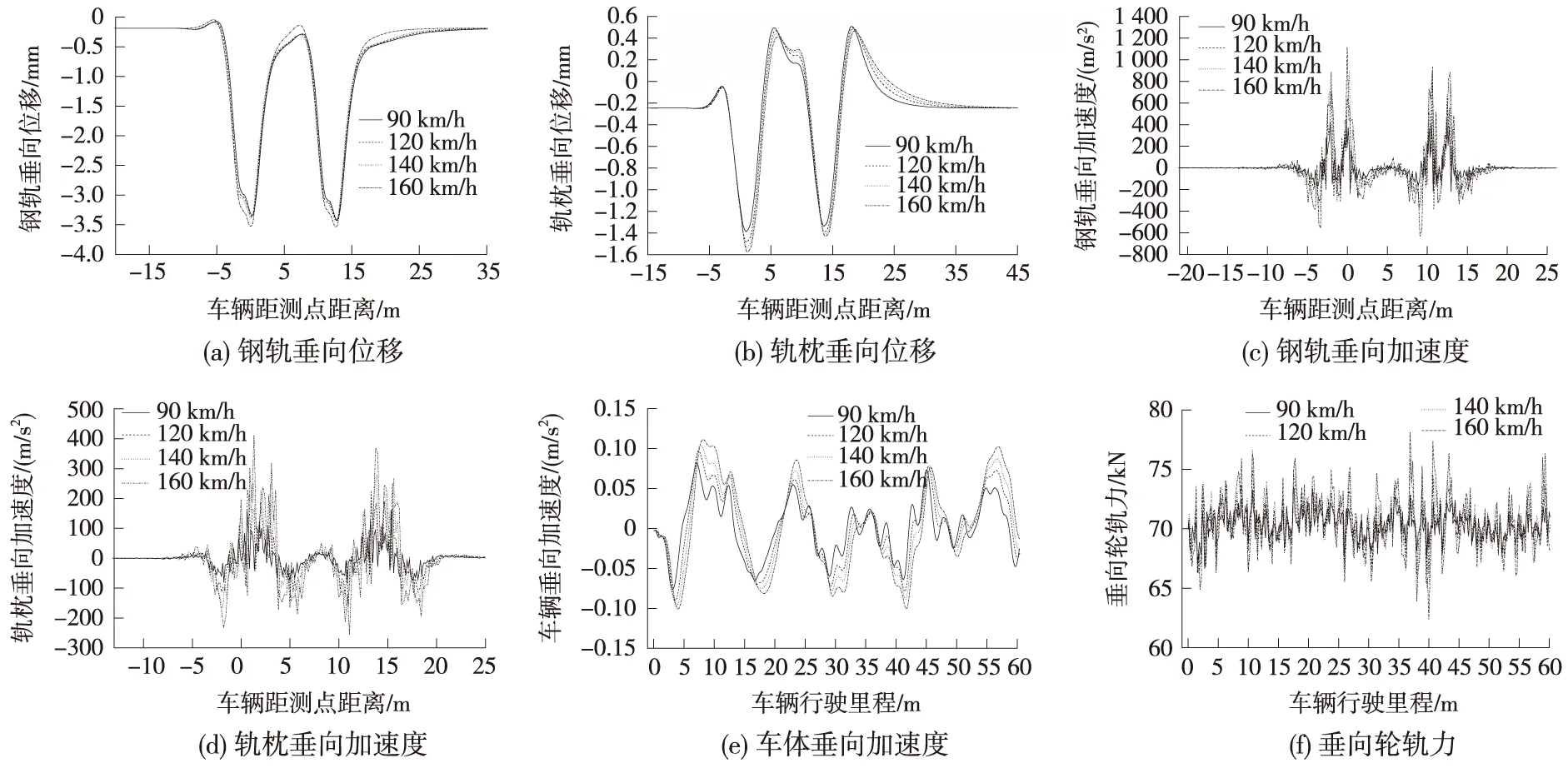
图4 不同车速对车辆和轨道结构垂向动力响应的影响

图4中横坐标“车辆距测点距离”指的是车辆前轮距离被测点的位置，下文一致。

表2 不同车速下各项指标最大值

当线路纵向坡度为0，分析不同的车辆行驶速度对梯形轨枕轨道结构的动力响应的影响结果，得出以下结论。

(1)车速的增加对钢轨和轨枕的垂向位移的影响较小。随着车速的增加，钢轨和轨枕垂向位移呈增大趋势，但其值变化都很小，车速从90 km/h增加到160 km/h，对应的钢轨垂向最大位移只增大了0.1 mm左右，而轨枕垂向最大位移增加了约0.18 mm。在车辆经过被测点位置时该点轨枕垂向位移达到最大值，车轮距离被测点大约10 m时开始对轨枕位移有较大影响。

(2)车速的变化对车辆和轨道振动加速度的影响很大。随着车速的增加，钢轨和轨枕加速度明显增大，车速从90 km/h增加到160 km/h，对应的钢轨加速度接近于线性增长，最大值增加了693.34 m/s2，增幅为162.7%；对应的轨枕加速度最大值增加了250.84 m/s2，增幅为155.3%。车辆垂向加速度逐渐增大，对应的车辆垂向加速度最大值增加了0.059 m/s2，增幅为77.61%，但不同车速下车体加速度变化趋势基本一致。

(3)随着车速的增加轮轨力逐渐增加，但其值变化相对较小，车速从90 km/h增加到160 km/h，对应的轮轨垂向力最大值只增加了1.96 kN，说明车速的变化对轮轨力的影响比较小。

(4)轮重减载率随着车辆运行速度的提高呈增加趋势，但是变化较小，不同车速情况下轮重减载率最大值为0.233。

2.2 不同坡度对车辆和轨道结构动力响应的影响

当车辆行驶速度为90 km/h，线路纵向坡度为按线路纵向坡度：无坡度、28‰顺坡、35‰顺坡和40‰顺坡变化时，对梯形轨枕轨道结构的动力响应进行分析，得到计算结果如表3和图5所示。

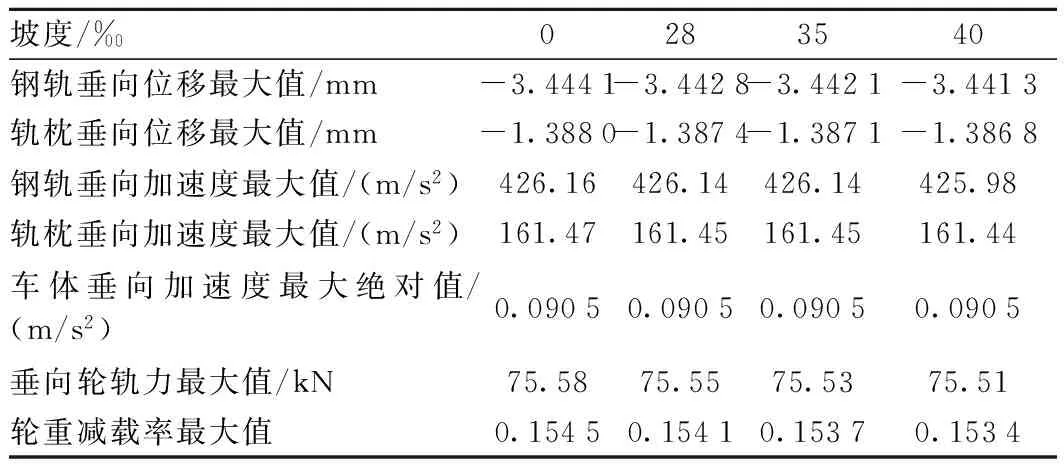
表3 不同坡度下各项指标最大值

当车辆行驶速度为90 km/h时，随着坡度的增加，不同的线路纵向坡度对梯形轨枕轨道结构的动力响应的影响有以下特点。

图5 不同坡度对车辆和轨道结构垂向动力响应的影响

(1)随着坡度增加，钢轨和轨枕垂向位移略有减小，坡度从0变化到40‰，对应的钢轨垂向最大位移减小了0.002 8 mm；而轨枕垂向最大位移减小了0.001 2 mm。

(2)不同坡度下车体垂向加速度变化趋势基本一致。而随着坡度的增加，车辆垂向加速度减小，坡度从0变化到40‰对应的车辆垂向加速度最大值减小了0.006 m/s2，其影响很小。

(3)钢轨和轨枕垂向加速度均减小，坡度从0变化到40‰，对应的钢轨垂向加速度最大值减小了0.18 m/s2，对应的轨枕加速度最大值降低了0.03 m/s2。由此可见，坡度的变化引起的钢轨和轨枕垂向加速度的变化很小。

(4)随着坡度的增加垂向轮轨力减小，坡度从0变化到40‰，对应的垂向轮轨力最大值减小了0.07 kN，不同坡度下垂向轮轨力变化趋势基本一致。

(5)不同坡度下车辆的轮重减载率随着纵向坡度的增大呈减小趋势，不同坡度情况下轮重减载率最大值为0.154。

3 结论

针对贵阳地铁一号线长大连续坡道上梯形轨枕轨道系统的垂向动力学特性进行研究，分析不同车辆行驶速度以及不同坡度对车辆和轨道结构的影响规律，结论如下。

(1)车速的增加对钢轨和轨枕的垂向位移的影响较小。车速从90 km/h增加到160 km/h，钢轨整体垂向位移呈减小趋势，轨枕垂向位移逐渐增大，但其值变化都很小，对应的钢轨垂向最大位移只减小了0.1 mm左右，而轨枕垂向最大位移增加了约0.18 mm。

(2)车速的变化对车辆和轨道结构垂向加速度的影响很大。车速从90 km/h增加到160 km/h，钢轨和轨枕垂向加速度明显增大，对应的车辆垂向加速度增幅达77.61%，钢轨垂向加速度增幅为162.7%，轨枕加速度增幅为155.3%。

(3)车体振动加速度是评价车辆舒适性最直接的标准。我国铁路车体垂向振动加速度的舒适度标准取为：0.13g(即1.275 m/s2)。车速从90 km/h增加到160 km/h，对应的车辆垂向加速度增幅达77.61%，车辆加速度最大值为0.135 m/s2<0.13g。

(4)车速的变化对轮轨力的影响比较小，车速从90 km/h增加到160 km/h，对应的垂向轮轨力最大值只增加了1.96 kN

(5)纵向坡度的增加对车辆和轨道结构的影响很小，而且只有在列车经过被测位置附近有很小的影响，由于坡道上轮轨垂向分力减小而纵向分力增加，因此导致坡道增加而所有动力学量值均减小，但其影响可以忽略不计。

(6)我国国标《铁道车辆动力学性能评定和试验鉴定规范》(GB 5599—1985)规定轮载轮重减载率安全指标允许限度为轮载轮重减载率不大于0.6；危险限度为轮载轮重减载率等于0.65[11]。各种工况下，梯形轨枕轨道系统的轮重减载率最大值为0.233，均未超限。

[1]畅德师.北京地铁梯形轨道工程试验段考察报告[J].铁道标准设计，2006(S1):140-143.

[2]邓玉姝，夏禾，善田康雄，井上宽美，齐琳.城市轨道交通梯形轨枕轨道高架桥梁试验研究[J].工程力学，2011(3):49-54.

[3]周宇，许玉德，李海峰.梯子式轨道结构系统[J].城市轨道交通研究，2002(1):21-23.

[4]刘学毅，王平.车辆-轨道-路基系统动力学[M].成都：西南交通出版社，2010.

[5]谢彦.基于ANSYS的梯形轨枕轨道结构减振性能分析[D].广州：华南理工大学，2010：24-31.

[6]陈伯靖，周建，李成辉.浮置式梯形轨枕轨道减振器刚度对轨道动力特性影响分析[J].铁道标准设计，2013(1):5-7.

[7]戴华明.城市轨通交通梯形轨枕减振性能研究[D].北京：中国铁道科学研究院，2011：22-39.

[8]刘晓静.地铁B型车转向架构架强度分析与研究[D].北京：北京交通大学，2010：5-8.

[9]北京城建设计研究总院.GB50157—2013地铁设计规范[S].北京：中国计划出版社，2013.

[10]张珍珍.梯形轨枕轨道力学性能分析.铁道勘测与设计[J]，2010(6):34-36，50.

[11]邓玉姝.釆用梯式轨枕轨道的城市轨道交通车桥动力响应分析及减振研究[D].北京：北京交通大学，2011：80-97.

[12]中华人民共和国国家质量检验检疫总局，中国国家标准化管理委员会.GB 5599—1985铁道车辆动力学性能评定和试验鉴定规范[S].北京：中国标准出版社，1985.

Study on Vertical Dynamics Response of Ladder Sleeper Railway Track on Large and Continuous Ramps

LI Juan1, LIU Xue-yi1, LIU Huan1, YUAN Yue-gan2

(1.MOE Key Laboratory of High speed Railway Engineering, Southwest Jiaotong University, Chengdu 610031, China;2.The Guangzhou Track Maintenance Division of Guangzhou Railway Incorporated Company, Guangzhou 510610, China)

Ladder sleeper railway track is the longitudinal sleeper railway system. The sleeper is composed of longitudinal prestressed concrete beam and horizontal steel pipe. Not only can it bring full play to the sleeper performance, but also greatly improve the dispersion ability of load. Ladder sleeper railway track is effective in the reduction of vibration and noise. An elastic foundation beam-plate model is established based on the features of ladder sleeper railway track. The vertical dynamic response of the ladder sleeper railway track at different operating train speeds and slopes is calculated and analyzed. The paper demonstrates the feasibility of laying the ladder sleeper railway track on large and continuous ramps.

Large and continuous ramp; Ladder sleeper; Finite elements method; Vertical dynamic response

2014-12-01；

2014-12-20

李 娟(1990—)，女，硕士研究生，E-mail：1210311774@qq.com。

1004-2954(2015)08-0035-04

U213.2+4

A

10.13238/j.issn.1004-2954.2015.08.008