基于Mamdani模糊神经网络的相敏轨道电路故障诊断方法研究

陆晓峰，王小敏，李光耀

(西南交通大学信息科学与技术学院，成都 610031)

基于Mamdani模糊神经网络的相敏轨道电路故障诊断方法研究

陆晓峰，王小敏，李光耀

(西南交通大学信息科学与技术学院，成都 610031)

针对25 Hz相敏轨道电路故障的不确定性与模糊性，提出一种基于Mamdani模糊神经网络的轨道电路故障智能诊断改进方法。采用自适应-动量BP学习调整法对模型参数进行训练优化，给出推导过程，并讨论系统参数初始值的设定。仿真实验表明，在相同实验条件下改进方法降低了训练误差，并有效地提高了诊断学习过程的稳定性与收敛速度，对25 Hz轨道电路故障进行智能模糊诊断是可行的。

轨道电路；故障诊断；Mamdani模糊逻辑；神经网络；自适应-动量

1 概述

轨道电路是现代高速铁路信号系统的重要组成部分，常年工作于室外恶劣环境，是故障多发设备，也是电务部门的重点维护对象。目前主要依靠维修人员经验结合现场状态进行轨道电路故障诊断，自动化和智能化水平较低。

近年来，一些先进的故障诊断理念与算法被尝试应用到轨道电路故障诊断中，以提高故障的自动智能诊断能力。文献[1]提出一种基于模糊推理的轨道电路智能故障诊断算法，对轨道电路模拟原件的短路、开路等硬故障有较好的效果。文献[2]给出基于遗传算法的轨道电路故障综合诊断方法，能对无绝缘轨道电路中补偿电容故障与道砟电阻波动等情况做出正确综合评判。文献[3]提出一种基于D-S数据信息融合的铁路信号设备故障诊断模型方法，提高了诊断结论的可信度。文献[4]以Mamdani模糊神经网络结构为基础，以站内25 Hz相敏轨道电路为研究对象建立故障诊断模型，为轨道电路故障诊断提供了新的思路，但经试验测试，该方法易陷入局部极小值、稳定性较低、收敛速度慢，影响诊断效果。

本文在文献[4]基础上，提出了一种基于Mamdani模糊神经网络的轨道电路故障诊断改进方法。主要工作是分析了系统参数的初始化取值，引入了自适应-动量BP学习调整法对模型参数进行训练优化，并给出了详细的推导过程。实验仿真结果表明，改进方法具备自学习自适应能力与模糊逻辑处理能力，有效地提高了诊断学习过程的稳定性和收敛速度，可以实现25 Hz相敏轨道电路的智能故障诊断。

2 Mamdani模糊神经网络结构

在故障诊断领域，将Mamdani模糊逻辑系统与神经网络结合，构建模糊神经网络模型(图1)，可用于不确定性和模糊性故障现象的智能诊断。

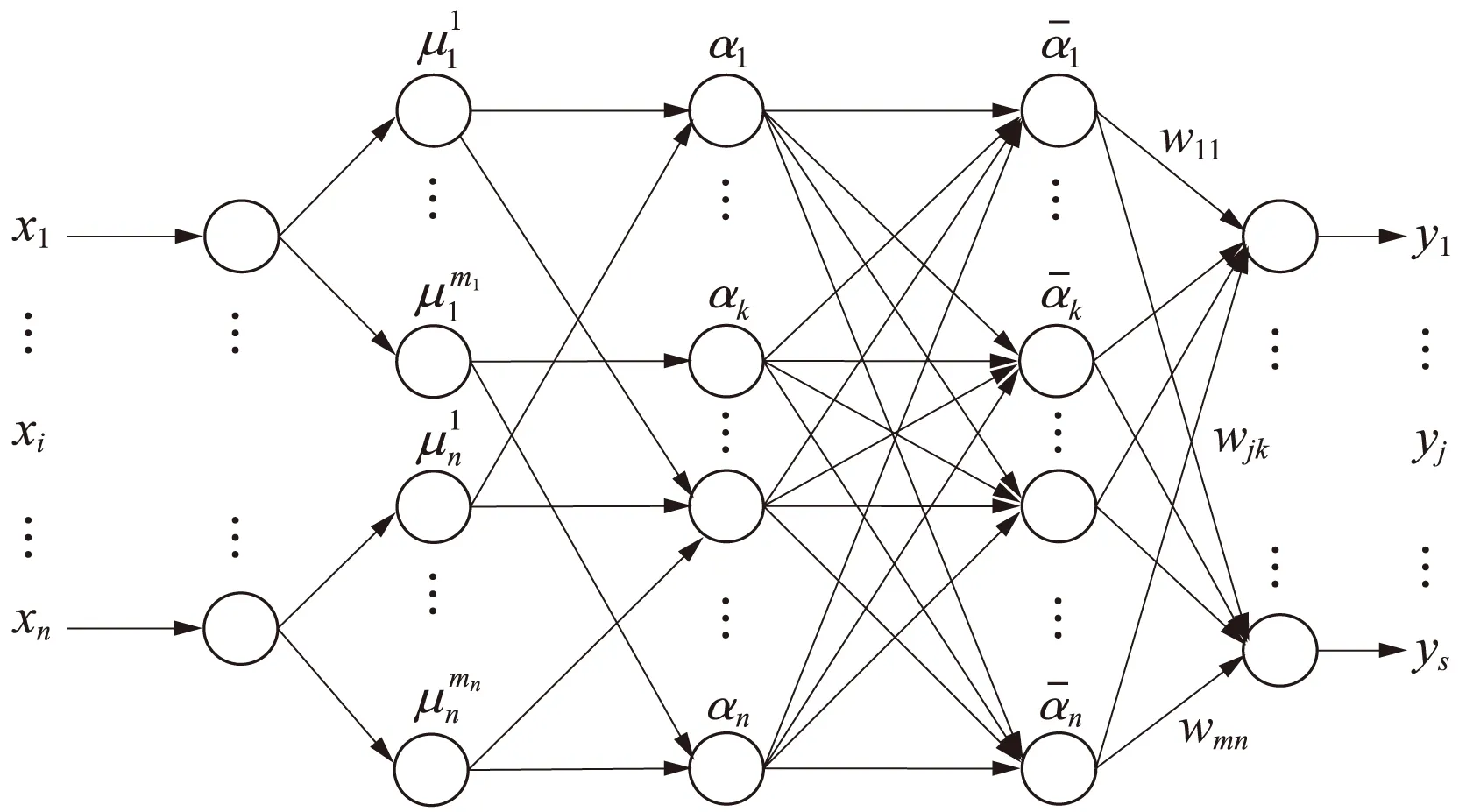
图1 Mamdani模糊神经网络模型

第一层为输入层，该层的节点直接与输入变量矩阵X的各个分量连接。

(1)

(2)

第三层为规则层，每个节点代表一条模糊规则，用来匹配模糊规则的前件，计算每条规则的适用度αk，即

(3)

其中，i1∈[1，2，3，…，m1]；i2∈[1，2，3，…，m2]，…；in∈[1，2，3，…，mn]；k=1，2，3，…，m，m为模糊规则总数。

对于给定的输入，只有在输入点附近的语言变量才有较大的隶属度值，远离输入点的语言变量值的隶属度极小或为0。当隶属度很小(如<0.005)时可近似取0，因此在αk中只有少量结点输出非0。

第四层为反模糊化层，实现模糊规则归一化运算，得出每条规则的激活度，即

(4)

第五层为输出层，进行清晰化计算，即

(5)

3 基于Mamdani模糊神经网络的相敏轨道电路故障诊断模型

以我国电气化铁路普遍使用的站内25 Hz相敏轨道电路为研究对象，结合其故障模式特点，文献[4]引入Mamdani模糊网络模型，分别建立了表1所示的系统输入输出关系和表2所示的故障模糊诊断规则。其中，每个系统模型输入都用“偏高(H)”“合适(N)”“偏低(L)”3个模糊子集描述，且用“极可能故障(A=0.9)”、“有可能故障(B=0.6)”、“偶然故障(C=0.2)”、“几乎不可能故障(D=0.05)”4个模糊语言对4个系统模型输出进行描述。

表1 系统模型输入与输出

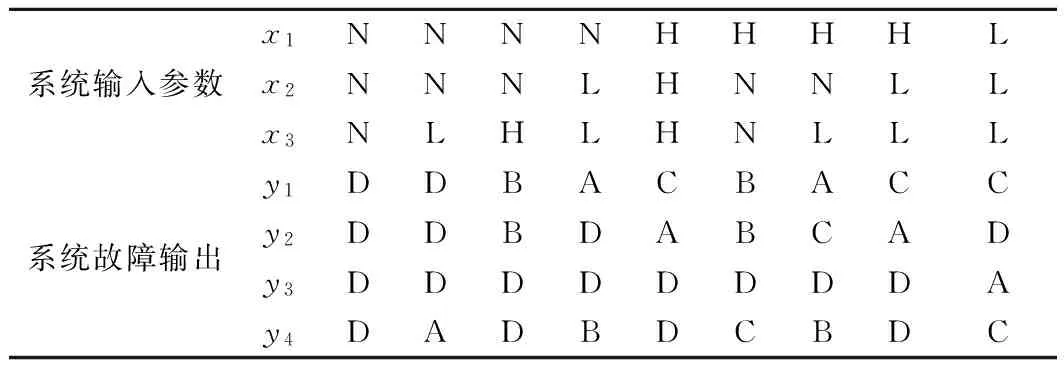
表2 25 Hz相敏轨道电路故障诊断规则

在此基础上，选定3个电压值作为系统输入，每个输入通过模糊处理分成3个模糊子集，通过9条模糊规则推理得到4个故障程度输出，建立了25 Hz轨道电路故障诊断模糊神经网络模型如图2所示[4]，为轨道电路故障诊断提供了一种新思路。

4 基于自适应-动量学习机制的Mamdani模糊神经网络故障诊断改进方法

经计算机仿真验证，文献[4]方法收敛速度较慢，且易陷入局部极小值，稳定性较低。本文在此基础上，引入自适应-动量BP学习调整法对其学习机制进行了改进优化，并分析了系统参数初始化取值，取得了较好的效果。

图2 25 Hz相敏轨道电路故障诊断模糊神经网络模型

4.1 自适应-动量BP学习机制

根据图2的模型结构与所采用的隶属度函数式(2)，可以看出系统需要进行训练调整的参数为输出层连接权值wjk以及高斯隶属函数的参数dij与σij。首先根据BP累积误差逆传法求解诊断系统模型的最优权值参数。

设样本对为{Tjs，yjs}，(j=1～L，s=1～N)，其中，L为模糊神经网络模型输出参数个数；N为学习样本对的数量。采用全局误差函数，Es为每次样本输入结果的误差，即

(6)

计算第五层输出层误差灵敏度为

(7)

计算第四层误差灵敏度为

(9)

计算第三层误差灵敏度为

(10)

在计算第二层误差灵敏度的过程中，令

(11)

(12)

则计算第二层误差灵敏度为

(13)

根据计算得到的各层误差灵敏度计算修改参数，其中η为学习率，取0.1：

(14)

(15)

(16)

为优化BP网络梯度下降学习过程的收敛速度和稳定性，增加系统学习效率，采用启发式调整方法，用新误差E(t+1)与旧误差E(t)的比值大小表示全局误差的变化情况，当全局误差E>10-10时，根据全局误差的变化信息对学习速率进行调整，若比值小于1，则可适当增加学习速率，若比值大于等于某固定值，则需要下调学习速率；当E≤10-10时，学习速率不再调整。调整规则描述如下

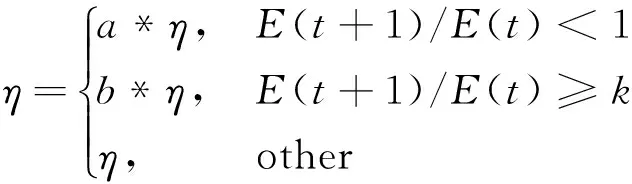
(17)

经测试，参数k=1.05、a=1.012 7、b=0.8时效果较好。

在调整过程中，为进一步优化算法，在自适应学习速率调整的基础上，引入附加动量因子，增强学习算法快速收敛性能，则参数调整改进过程如下

(18)

(19)

4.2 系统参数初始化分析

在轨道电路故障诊断网络模型中，网络参数的初始化至关重要，连接权wjk的值为(0，1)之间的随机数，采用伪随机数发生器自动生成。系统参数初始化的关键在于隶属度函数参数dij和σij的初值确定，其大小直接影响模糊判断的结果，下面讨论其初始化方法。

在给出基本思路前，先引入重叠度的概念。所谓重叠度是指两个模糊子集重叠的程度，用这两个模糊子集交集的最大隶属度来表示。在模糊控制中，重叠度是影响控制性能的一个重要因素，重叠度过大或过小都会降低控制效果，通常应控制在0.5左右。基于该原则，推导初始期望值的确定公式。

聚类中心即dij的值，采用基于数据的方法，应用平均数法通过加权平均或取中点法取最大值与最小值的中间点确定。在25 Hz相敏轨道电路故障诊断中，根据现场故障数据结合专家经验，按上述方法得到各模糊子集的隶属度函数中心初值矩阵

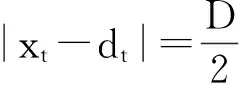
(20)

因此，σij的计算采用如下公式

(21)

其中，γ为重叠系数，一般取值为1.5。

按上述方法，根据之前得到的隶属度函数中心初值矩阵d计算得到各模糊子集隶属度函数宽度初值矩阵

在25 Hz相敏轨道电路故障诊断中，各模糊子集隶属度函数参数dij和σij的初始化是学习训练得到正确故障诊断模型的关键。若其初值设置不当，使隶属度函数的模糊识别作用降低甚至失效，将会直接影响学习调整过程，使训练过程中全局误差E的收敛无法达到要求，导致诊断模型建立失败。以送端输出电压为例，经过上述隶属函数参数初始化计算后，得到送端输出电压的模糊隶属度函数如图3所示，3个模糊子集之间重叠度大约为0.55，且符合由低到高的语义顺序，避免了模糊子集间不恰当的重叠，模糊描述清晰，使模型初步具备较好的模糊表达功能。

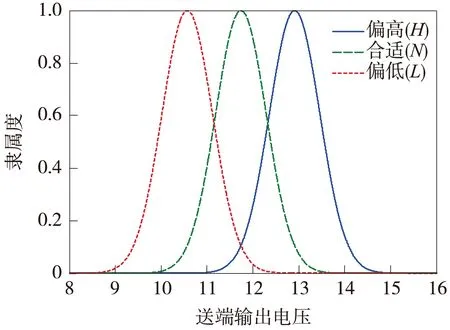
图3 送端输出电压模糊隶属函数

5 仿真实验

5.1 方法分析对比

本文在VC++6.0环境下搭建了25 Hz相敏轨道电路故障诊断系统实验仿真平台，验证设计方法的可行性。分别对文献[4]方法、自适应学习速率法、本文自适应-动量法应用样本数据进行训练，得到的训练全局误差E如图4所示。

图4 算法改进前后系统网络学习训练误差结果对比

从图4(a)中可以看出，自适应学习速率法能一定程度上降低收敛误差，但收敛前期的优化效果不明显；图4(b)则表明，在自适应学习速率基础上引入增加动量法，能明显提高收敛速度并降低收敛误差，从而有效提高故障诊断系统的收敛速度与准确性。结合表3数据可知，本文的自适应-动量优化法在学习训练初期，由于初始误差的存在，全局误差E初始值较大，经前15次训练急速降低，之后进入平缓调整期，进一步使E收敛，在第50步时全局误差约为0.000 5，在100步时，全局误差约为4×10-10，很好地满足系统准确性要求。

表3 算法改进前后全局误差数据分析对比

5.2 调整过程与诊断验证

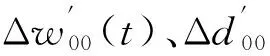
图5 训练调整过程观察

为验证算法与模型的可靠性与有效性，本文利用模拟样本数据作为输入进行验证，结合故障诊断规则表2，得到系统输出及诊断结果如表4所示。可以看到故障诊断结果是正确的，符合系统设计要求。

表4 模拟数据故障诊断结果

在实际应用中，可根据现场经验和专家知识，进一步细化故障模式和扩充诊断规则表2，在本文方法基础上，将训练结束得到满足条件的网络模型保存为模板，然后将轨道电路微机监测采集的现场数据输入到训练好的系统网络模型中，根据故障输出结果得到轨道电路故障发生的可能原因和故障处理意见，逐步实现25 Hz轨道电路故障的智能诊断。

6 结语

轨道电路作为影响铁路运输效率和行车安全的关键设备，在故障发生时应尽快找出故障原因并给予解决，提高设备的可靠性与安全性。本文在文献[4]方法的基础上，构建25 Hz相敏轨道电路智能故障诊断系统模型，将模糊逻辑与神经网络学习机制相结合的方法融入到智能故障诊断技术中，采用自适应-动量学习算法进行优化，提高了学习过程的稳定性、准确性以及收敛速度。该方法自学习能力强、收敛速度快，能较好地模仿专家思维评价方法给出故障诊断结果，为轨道电路的智能诊断和日常维护提供一定的参考价值。

[1] 刘琰琼.ZPW-2000A轨道电路智能故障诊断算法应用研究[J].铁路通信信号工技术，2014(1):29-32.

[2] 赵林海，冉义奎，穆建成.基于遗传算法的无绝缘轨道电路故障综合诊断方法[J].中国铁道科学，2010(3):107-114.

[3] 李娜，董海鹰.基于D-S证据理论信息融合的轨道电路故障诊断方法研究[J].铁道科学与工程学报，2012，9(6):107-112.

[4] 黄赞武，魏学业，刘泽.基于模糊神经网络的轨道电路故障诊断方法研究[J].铁道学报，2012(11):54-59.

[5] 马涛，米根锁，齐东.基于灰色理论ZPW2000A无绝缘轨道电路故障风险分析[J].铁道标准设计，2013(4):115-118.

[6] 王彤.基于最小二乘支持向量机的轨道电路故障诊断方法[J].铁道标准设计，2014(2):89-93.

[7] 武剑辉，杨学良.模糊BP神经网络及其在故障诊断中的应用[J].系统工程与电子技术，2001(10):73-75.

[8] 杨慧，邓征.基于自适应神经网络的飞机突发故障诊断研究[J].计算机工程与设计，2014(3):1010-1015.

[9] 苏羽，赵海，苏威积，等.一种基于模糊神经网络的融合故障诊断方法[J].计算机工程，2004(17):5-6，170.

[10]李雅美，魏文军.基于模糊神经网络的道岔故障诊断系统研究[J].铁路计算机应用，2012，21(1):35-38.

[11]潘昊，田捷，钟珞.前向多层神经网络的步长搜索调整研究[J].计算机工程与应用，2004，17(7):17-18.

[12]Chen J， Roberts C， Weston P. Fault Detection and Diagnosis for Railway Track Circuits Using Neuro-fuzzy Systems[J]. Control Engineering Practice， 2008，16(5):585-596.

[13]Chen B， Hoberock L L. A fuzzy neural network architecture for fuzzy control and classification[C]∥Neural Networks， 1996.， IEEE International Conference on. IEEE， 1996，2:1168-1173.

Research on Phase-sensitive Track Circuit Fault Diagnosis Based on Mamdani Fuzzy Neural Network

LU Xiao-feng， WANG Xiao-min， LI Guang-yao

(School of Information Science and Technology， Southwest Jiaotong University， Chengdu 610031， China)

Addressing the uncertainty and fuzziness of 25 Hz phase-sensitive track circuit faults， this paper proposes an improved track circuit fault diagnosis method based on Mamdani fuzzy neural network. The adaptive-momentum BP learning method is used to train and optimize model parameters with the derivation process and the setting of initial value of system parameters is discussed. Simulation results show that under the same experimental conditions， the improved method reduces the training error and effectively improves the stability and convergence speed of the learning process. Application of this method to 25 Hz phase-sensitive track circuit faults diagnosis is of high feasibility.

Track circuit; Fault diagnosis; Mamdani fuzzy logic; Neural network; Adaptive-momentum

2015-03-19；

2015-03-28

中国铁路总公司科技研究开发计划课题(2013X012-A-1，2013X012-A-2，2014X008-A)

陆晓峰(1990—)，男，硕士研究生。

王小敏(1974—)，男，博士，教授，博士生导师，主要研究方向为轨道交通信息化安全工程，E-mail:xmwang@swjtu.edu.cn。

1004-2954(2015)11-0104-06

U284.2

A

10.13238/j.issn.1004-2954.2015.11.025