变刚度支撑对船舶轴系横向振动影响分析

李小军,朱汉华，杨 文，刘 乐，杨宗榕

(武汉理工大学 能源与动力工程学院， 湖北 武汉 430063)

变刚度支撑对船舶轴系横向振动影响分析

李小军,朱汉华，杨 文，刘 乐，杨宗榕

(武汉理工大学 能源与动力工程学院， 湖北 武汉 430063)

为研究轴承水平和垂直变刚度对船舶轴系横向振动的影响，在ANSYS中建立船舶推力轴系有限元模型，通过模态分析和谐响应分析，研究了艉轴承2个共轭方向变刚度时，轴系的横向固有振动频率以及横向受迫振动情况。研究结果表明：随着轴承某一方向的刚度降低时，该方向上横向振动的固有频率也降低，尤其是低阶频率，对应的谐响应振幅也随之降低，这对轴系低阶横向振动影响较为突出。该结果对通过改变轴系支撑刚度来抑制轴系振动提供了理论支持。

船舶轴系; 横向振动；模态分析； 谐响应分析

船舶在实际运行中，由于轴系支撑刚度的变化、旋转质量的偏心、螺旋桨上的伴流激振力以及螺旋桨偏心质量的综合作用，会使推进轴系产生多种振动，其中横向振动尤其强烈，引起船体震颤、轴承磨损和轴系疲劳，危害突出，国内外对轴系横向振动的研究高度关注[1]。

通常在计算轴系临界转速时，由于缺少关于轴承刚度及其支座刚度的资料，一般都采用简化算法，即假设轴承为绝对刚性，同时其水平刚度和垂直刚度相同。随着船舶大型化，轴与轴承的刚度可能接近一个数量级，常用船舶轴承刚度如表1所示，这种简单的刚度简化算法会带来较大误差[2]。

本文以变刚度的方法，建立有限元模型，应用ANSYS模态分析和谐响应分析模块，分析轴承水平和垂直刚度变化时轴系的横向振动特性，为进一步研究船舶轴系振动控制奠定基础。

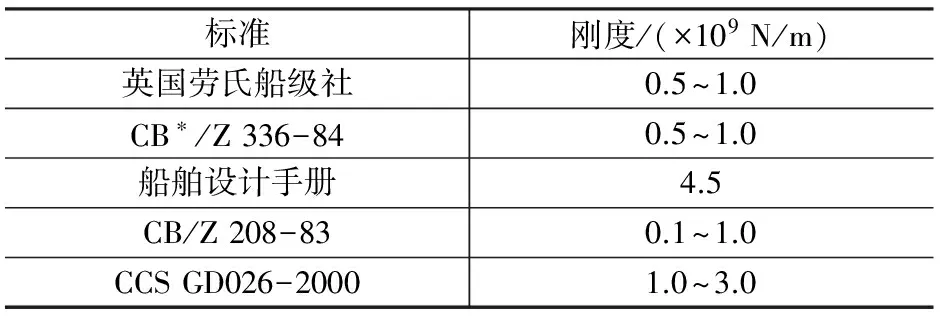
表1 常用船舶轴承(合金)刚度

1 轴系振动分析方法

1.1模态分析理论

模态分析方法是研究结构动力特性的一种方法，是系统辨别方法在工程振动领域的应用。模态是机械结构的固有振动特性，每一个模态具有特定的固有频率、阻尼比和模态振型。这些模态参数可以计算或者实验分析得到，计算或实验过程称为模态分析。根据振动理论，多自由度系统以某个固有频率振动时所呈现出的振动形态称为模态。此时各点位移存在一定的比例关系，称为固有振型。

对于一个具有N自由度线性系统，其运动微分方程:

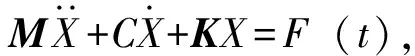
(1)

式中：M为质量矩阵；K为刚度矩阵；X为位移向量；F(t)为作用力向量，t为时间;C为阻尼系数。

当F(t)=0时，忽略阻尼C影响，方程变为：

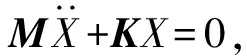
(2)

自由振动时，结构上各点做间谐振动，各点位移X：

X=φ-ejωt，

(3)

由式(2)、式(3)得：

(K-ω2M)φ=0。

(4)

根据以上公式求出特征值ω2和特征值φ，其中ω=2πf，f为频率。求得系统各阶固有频率便是模态频率，固有阵型便是模态振型。

1.2谐响应分析理论

通常意义上的谐响应分析是指在某一指定的频率范围内，结构受到循环载荷作用而产生相应的随频率变化的结构响应，并且做出响应——频率线型图，从图1可判别响应的峰值及对应的结构应力。整体结构的动力平衡方程：

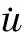
(5)

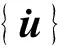
2 分析实例

2.1分析对象的基本参数

该船轴系全长24 320 mm，由1根螺旋桨轴、3根中间轴组成，5个轴承支撑， 分别是1个后艉轴承、1个前艉轴承、3个中间轴承。

轴系的主要参数如下：螺旋桨直径，1 380 mm,附水质量为1 800 kg;轴外径为480 mm。轴材料为34CrMo1，密度为7 800 kg/m3，弹性模量207 GPa，泊松比为0.25。

1) 采用BEAM188梁单元来模拟船舶轴系，Z轴为轴方向，联轴节和法兰盘可以用BEAM188设置不同直径的梁截面来模拟。

2) 轴系的轴承采用COMBIN14弹簧单元进行模拟，在推进轴系的水平和垂直方向分别设置2个弹簧[3]。弹簧单元的一端与轴承对应的节点相连，另一端为固定端，进行全约束。

3) 在轴系和齿轮箱法兰的连接处，视为刚性连接，对其进行Z轴方向约束。

4) 对于螺旋桨，根据质量守恒定律和转动惯量守恒定律，将螺旋桨转换为质量和转动惯量均和螺旋桨相同的圆盘，采用BEAM188梁单元模拟[4]。经过简化，轴系的有限元模型如图1所示。

2.3模态分析

为了研究轴承支撑刚度对推进轴系振动的影响规律，以轴承刚度4.6×109N/m为基准[5]，分别按轴承水平刚度为2.3×108N/m、垂直刚度为4.6×109N/m；轴承水平刚度为4.6×109N/m、垂直刚度为4.6×109N/m；水平刚度为4.6×109N/m、垂直刚度为4.6×109N/m；水平刚度为4.6×109N/m、垂直刚度为4.6×109N/m时4种不同情况进行模态分析，得到轴系振动的前10阶固有频率。

2.3.1 轴承刚度变化对轴系横向振动固有特性的影响

由于客观条件的变化与发展，教师的角色在人们心目中已发生变化，原初的“师者，所以传道、授业、解惑也”的教师定位已不能适应社会发展的新要求和定位。这就要求我们重新定位教师的角色，单纯“传道 授业 解惑”的教师角色，能否继续满足社会发展的新要求？面对教学对象、教学条件及教学环境的多样化，如何科学地、准确地定位教师的角色，这对全面、持续、有效地推进教师z专业发展，培养出高质量现代化人才，具有重要意义。

在分析轴系横向振动时，需要对轴系进行边界条件的约束，约束其Z方向(轴向)的平动自由度，约束X、Y、Z3个方向的转动自由度，保留沿X、Y方向的平动自由度[6]，由此计算得到的推进轴系固有频率结果如表2。

表2 水平刚度不同时横向振动频率

以上结果说明，轴承支撑刚度对推进轴系的横向振动频率有影响，随着水平刚度逐渐增大，轴系的横向振动频率也随之增大，低阶频率影响明显。当其水平刚度增大到和垂直刚度相当时，其一阶横向振动频率和二阶横向振动频率相同。

2.3.2 垂直和水平刚度不同分别对水平和垂直方向振动影响

为进一步研究轴承水平刚度变化对轴系垂直和水平方向横向振动的影响，仍以垂直刚度4.6×109N/m为基准，通过改变水平方向刚度值，观察各方向振动情况。对轴系进行边界条件的约束，约束其Z方向(轴向)的平动自由度，约束X、Y、Z3个方向的转动自由度，分别保留沿X、Y方向的平动自由度。此计算分别得到水平和垂直方向前10阶振动频率，如图2所示。

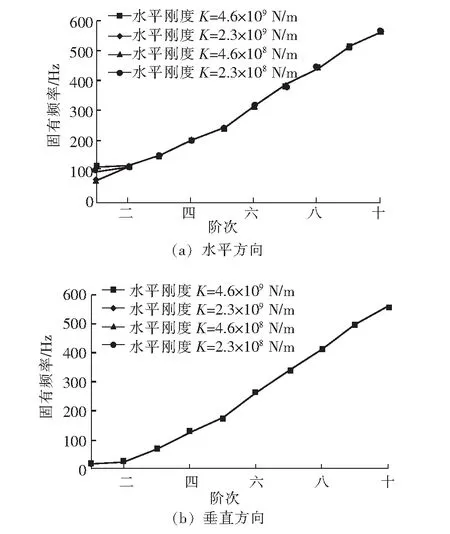
图2 变刚度条件下前10阶频率图

通过图2的对比，结合表2可以看出，随着轴承水平刚度的增大，轴系水平方向的各阶固有频率增大，其中一阶频率明显增大，高阶部分频率略微增大。而垂直方向的各阶固有频率均不变，这说明轴承在某方向上的刚度只会影响该方向的横向振动固有频率，与其他方向上的横向振动固有频率无关。

2.4谐响应分析

模态分析可以得到船舶轴系的各阶振型，但这只能表示出船轴各处的相对振动情况，而螺旋桨激励下各阶振型对轴系振动作用大小是不同的，对轴系进行谐响应分析，能得到轴系在螺旋桨激振力干扰下的振动情况[7]。

2.4.1 水平刚度和垂直刚度相同时谐响应分析

轴承水平刚度和垂直刚度均为4.6×109N/m时，对弹簧的固定端进行全约束，对梁单元分别只保留X、Y方向自由度，将螺旋桨的径向激振力FX=4 200 N，FY=4 200 N和径向激振力矩MX=64 200 N·m、MY=64 000 N·m加载螺旋桨对应的节点上，然后采用谐响应分析进行强迫振动计算[8]。其幅频响应曲线如图3所示。

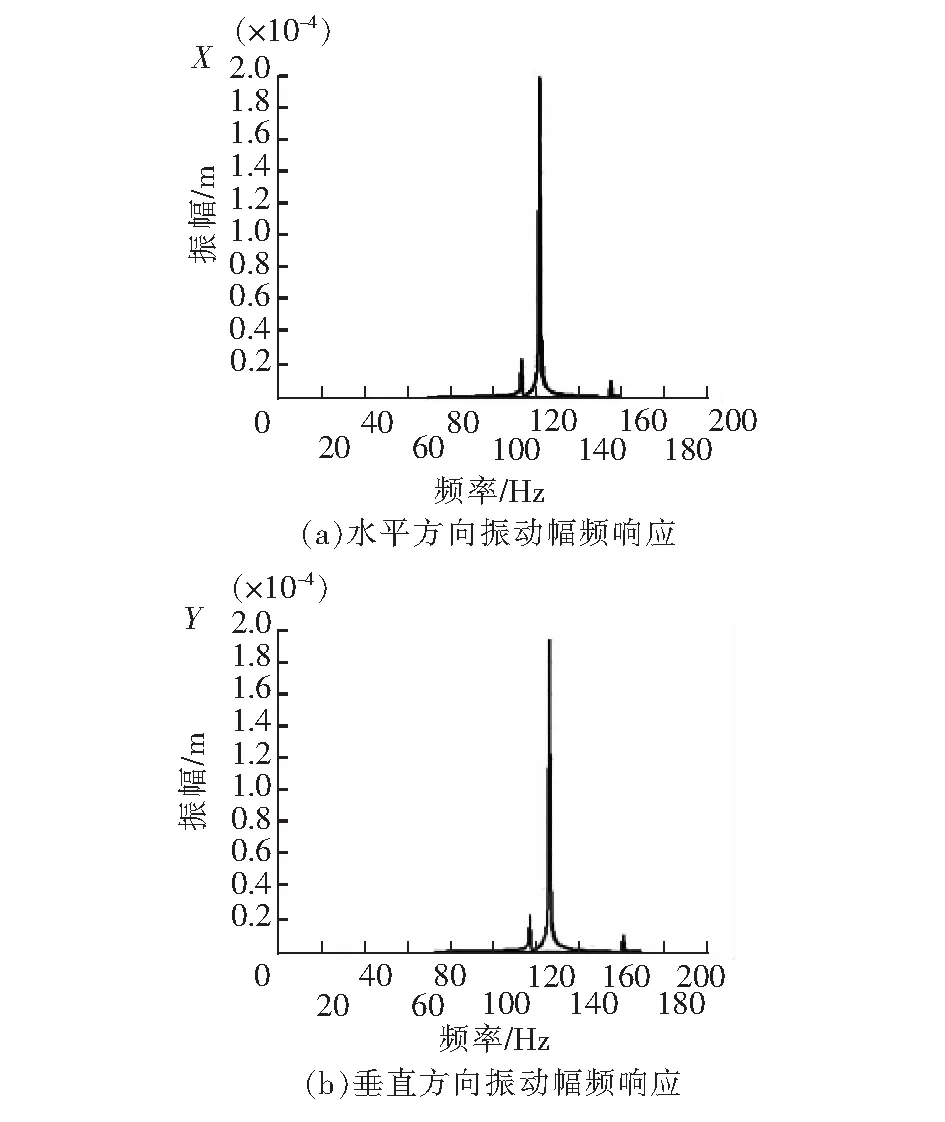
图3 水平刚度和垂直刚度相同时幅频曲线图

2.4.2 水平刚度变化时谐响应分析

轴承垂直刚度为4.6×109N/m、水平刚度为4.6×108N/m时，对弹簧的固定端进行全约束，对梁单元分别只保留X、Y方向自由度，将螺旋桨的径向激振力FX=4 200 N，FY=4 200 N和径向激振力矩MX=64 200 N·m、MY=64 000 N·m加载螺旋桨对应的节点上，然后采用谐响应分析进行强迫振动计算。 其幅频响应曲线如图4所示。

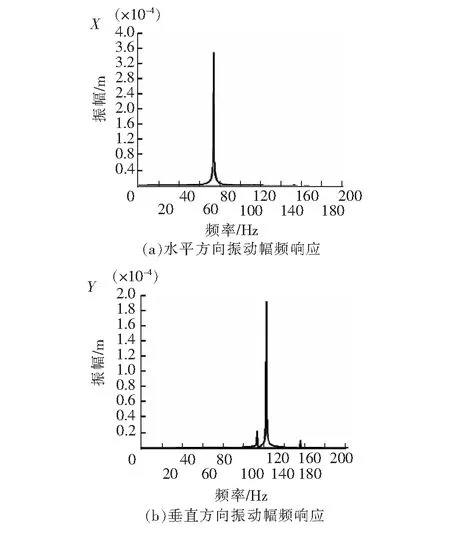
图4 水平刚度变化时幅频曲线图

通过图3和图4的可以看出以下几点。

1)在螺旋桨的激振力和激振力矩下，当轴承水平刚度和垂直刚度相当时，轴系在水平和垂直方向发生最大响应时的频率一样，均在120 Hz左右，与模态分析的结果相吻合。同时两者的谐响应振幅均为2×10-4m。

2)在螺旋桨的激振力和激振力矩作用下，当轴承垂直刚度为4.6×109N/m、水平刚度为4.6×108N/m时，轴系在水平和垂直方向发生最大响应时的频率不一样，水平共振频率为73 Hz左右，垂直共振频率仍然是在120 Hz左右，这与模态分析结果吻合。同时，水平振动的谐响应振幅为3.6×10-4m附近，而垂直振动的谐响应振幅仍然为2×10-4m左右。

3)通过图3和图4的对比分析可以看出，当轴承水平刚度和垂直刚度不同时，其在水平方向和垂直方向的共振频率和最大振幅均独立且不相同。

3 结束语

针对轴承水平和垂直方向上的刚度差异，本文尝试利用ANSYS仿真对船舶推进轴系进行模态分析和谐响应分析，具有较好的精度，可以满足工程需要，主要结论如下。

1) 轴承的刚度变化对横向振动有影响，而且轴承在某方向上的刚度只会影响该方向的横向振动固有频率，而不会影响到其他方向上的横向振动固有频率。

2) 随着轴承某一方向的刚度降低时，该方向上横向振动的固有频率也降低，尤其是低阶频率，对应的谐响应振幅也随之降低。

3)由于轴承水平和垂直方向上刚度的不同，会对横向振动特性产生一定影响，基于假设轴承水平和垂直刚度均为绝对刚度的简化方法会带来误差。因此，在进行船舶轴系机械振动设计和校核时，一定要充分考虑这一因素。

[1]Kim Chuel-Hyun, Lee Chang-Ho, Goo Ja-Sam. A dynamic response analysis of tension leg platforms includinghydrodynamic interaction in regular waves [J]. Ocean Engineering, 2007, 34 (11 /12): 1680-1689.

[2]周春良，刘占生，郑洪涛，等.轴承支承长度及间距对船舶轴系振动特性影响[J]. 船舶工程，2007(5)：33-36.

[3] 荀振宇，孙长江，沈红宇.船舶艉轴承接触压力分布及其影响因素研究[J]. 船海工程，2010(3)：48-50.

[4] 周瑞平.基于VB的船舶轴系回旋振动计算软件[J].造船技术，1999(3) ：30-33.

[5] 陈锡恩，高景.船舶轴系回转振动计算及其参数研究[J]. 航海工程，2001(5)：8-11.

[6]杨承三.输出轴支承轴承刚度对三环减速机动态性能的影响分析[J]. 机械工程师，2009(2)：52-53.

[7] 陈之炎.船舶推进轴系振动[M]. 上海：上海交通大学出版社，1987.

[8] 刘正林，周建辉，刘宇.计入艉轴倾角的船舶艉轴承液膜压力分布计算[J]. 武汉理工大学学报，2009(9)：111-113.

In order to study the effect of horizontal and vertical stiffness of bearing on shafting transverse vibration,the finite element model of ship shafting was established with the software ANSYS.Through the model analysis and harmonious respones analysis,the change of shaft transverse vibration was analyzed through adjusting the stem tube bearing stiffness of two conjugate direction.The calculation results show that as stiffness of bearing decreases at a certain direction,the transverse natural vibration frequency on this direction is reduced.The harmonic response amplitude decreases too,the effect on low order transverse vibration of shafting is obvious especially.It provides the theory support for suppressing the shafting vibration by changing the bearing stiffness.

shipping shaft system;transverse vibration;model analysis;harmonic response analysis

国家自然科学基金重点项目(NO.51139005)

李小军(1994-)，男，江苏南通人，在读本科生。

U664.2

10.13352/j.issn.1001-8328.2015.03.011

2015-03-26