地形图扫描数字化成图精度的研究

董增勋 侯 宇

(北京四达贝克斯工程监理有限公司石家庄分公司，河北 石家庄 050000)

引言

精度问题是确定地形图扫描数字化方法优势的主要原因之一。本文从扫描数字化的基本过程出发，在分析了地形图扫描数字化的误差来源基础上、通过讨论误差质量控制方法，估算成果数据能达到的精度，分析误差分布规律，以及进行具体实验的验证。

1、地图扫描数字化作业过程

外业采集数据→地形图的生成与编绘→扫描图纸预处理图纸扫描→图像定向与几何纠正→栅格图像矢量化→矢量数据与原图坐标的提取→误差分析→图形输出。

2、地形图扫描数字化误差来源

2.1 原图的误差来源:地图固有误差;纸张变形产生的误差。

2.2 扫描数字化过程中的误差:图纸扫描误差;扫描原图比例尺误差;图纸定向误差:几何纠正误差;屏幕数字化误差。

2.3 图形输出误差:显示器误差和打印误差。

3、扫描过程误差质量控制

3.1 原图误差控制

应将原图纸存放在适宜的温度和湿度的环境中。在图纸扫描之前对图纸进行预处理，如清洁图面、除去污点等，以保证图面清晰。

3.2 扫描数字化过程中的误差控制

(1)地图扫描精度控制

选取适当的扫描分辨率。对于平地地图采用分辨率300dpi即可满足精度要求，对于山区地形扫描分辨率应不低于500dpi。

(2)图像定向误差控制

定向精度控制在0.10mm～0.15mm 之间。

(3)几何纠正误差控制

并将几何纠正点位中误差精度控制在0.50mm 以内。

(4)屏幕数字化误差控制

矢量化误差控制:提高工作者的劳动效率。

软件误差的控制:尽量让软件研究者将软件产生误差的可能性降低到最低限度。弄清误差的产生和传播。

采样误差控制:通过数学计算的方式得出每个采样点的精确坐标。

3.3 图形输出误差控制

一般由分辨率决定。当分辨率达到300 dpi 时，误差可控制在0.085 mm 以内。

4、实验

4.1 实验步骤简述

(1)全站仪野外地形数据采集与数据处理。

(2)地形图的绘制与编辑与输出图纸输出。

(3)图纸扫描。

(4)图像定向与几何纠正。

(5)栅格图像的矢量化。

(6)提取采样点精确坐标计算。

(7)精度评定。

4.2 实验误差来源及其质量控制

经过分析以上工作过程中出现的主要误差来源及其控制方法如下:

地图固有误差:外业数据采集过程中的仪器观测误差、碎步点展点误差、图形输出误差等误差来源。由于这些误差的关系很难确定，因此很难对其进行综合评定。

原图变形误差:是由于图纸周围温度和湿度的变化而产生的误差。

误差控制方法:将原图纸存放在了温度、湿度适宜的环境中并进行了清洁图面、除去污点等预处理。

·扫描变形误差:主要来源是由于扫描仪分辨率的不同而产生的。

误差控制方法:由于实验中扫描仪分辨率选取300dpi。

·定向与几何纠正误差:主要是受数学模型的因素而引起的。

误差控制方法:可计算其结果的点位中误差是否在0.5mm 以内。

·屏幕数字化误差:主要包括图像矢量化误差、软件误差以及采样点精度误差。

4.3 实验精度分析

(1)变形误差精度分析

实验中对于变形误差的影响，利用原图与扫描后图纸的任意定向点间距离进行比较。计算中选取了四个顶点间距离为研究对象。

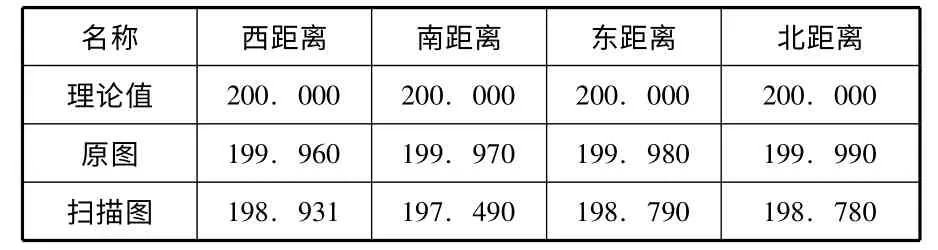
表4 -1 图纸变形与扫描变形比较(单位:mm)

由表4-1 可知道，扫描原地形图的误差中，原图扫描变形误差相对小，而扫描变形误差相对影响大。

(2)采样点坐标精度分析

采样的精度是影响到成图的精度的另一因素，因此必须考虑。获取采样点精确坐标的方法如下:设用鼠标取得其重心的概略位置为(u0，v0)，据此可得目标点的图像边界点分别为(ui，vi)(I=1，2，…，n)，其中n 为边界点个数，则采样点的坐标可求得:

依次类推，可得60 个采样点精确坐标。

(3)几何纠正精度分析

对扫描后的图像的几何纠正的精度，可以用点位中误差来表示，即:

由于0.2906 ＜0.50mm 所以点位精度满足几何纠正精度要求。

4.4 屏幕数字化精度分析

(1)数字化坐标数据的误差估计

就是将数字化后的空间数据与原地形图的数据进行机抽样比较，量测出点位的误差，然后利用统计分析，求出空间数据的精度指标。包括:均值中误差σx，σy，协方差σxy。

通过计算可以看出扫描数字化的误差在0.01m 以内，此结果表明扫描数字化与手工数字化的精度基本一致。

(2)均值检验

采用非正态总体均值检验中的单边检验方法，一般设总体Z 的分布函数为E (Z)，总体均值为Z，标准差为S，构造检验统计量［6］，计算结果如下表4-2。

表4 -2 x、y 统计量表

从表4-5 中可以看出计算的所有统计量均大于分位值，说明其均值不为0，表明扫描数字化过程有系统误差的影响。系统误差由光栅图纠正后的剩余误差、矢量化软件误差等构成。

(3)皮尔逊检验法误差分布检验

假设:H0:F (x)=F0 (x)，总体服从正态分布;H1:F (x)≠F0 (x)，总体不服从正态分布。通过计算可得:

表4 -3 误差分布

从表4-3 中可以看出各样本皆拒绝原假设，即χ2x ＞)，因此表明扫描数字化的误差分布不服从正态分布。

4.4 实验总结

扫描仪分辨率为300dpi 时，在扫描原地形图的误差中，原图变形误差相对小，而扫描图纸变形误差相对影响大;在对图像进行几何纠正时其纠正精度应控制在0.50mm;采用扫描数字化数据的精度与手扶跟踪数字化数据的精度基本一致，但其误差并不服从正态分布，更多地表现出系统性。

5、结论

本文从扫描数字化的基本原理过程出发，分析了地形图扫描数字化的误差来源以及质量控制方法，估算成果数据能达到的精度。并通过实验进行了验证，本次实验的精度分析对减弱系统误差，以及在减弱系统误差影响的基础上进一步探讨地形图扫描数字化数据的误差分布和精度具有一定的意义。

［1］余晓红.地图扫描数字化的误差分析［J］.测绘科学，2001，26 (4):49～52.

［2］胡晋山，马明栋，李博.地形图扫描数字化质量控制［J］.测绘通报，2004，1 (12):53～55.

［3］花向红，潘正风.扫描数字化地图数据的误差构成及精度分析［J］.武汉科技，1996，20 (4):16～28.

［4］扶卿华，倪绍祥，郭剑.栅格数据矢量化及其存在问题的解决［J］.现代测绘，2004，27 (3):8～11.

［5］曾衍伟.地形图扫描数字化精度分析［J］.四川测绘，2003，26 (2):82～85.

［6］高雷阜，李伟.新编概率论与数理统计［M］.第1 版.东北大学出版社，2000.215～249.