基于MATLAB/GUI的蜗线齿轮副节曲线设计*

□ 刘永平 □ 章慧成 □ 余 俊 □ 张庆飞

兰州理工大学 机电工程学院 兰州 730050

基于MATLAB/GUI的蜗线齿轮副节曲线设计*

□ 刘永平 □ 章慧成 □ 余 俊 □ 张庆飞

兰州理工大学 机电工程学院 兰州 730050

根据非圆齿轮啮合原理，针对蜗线齿轮副节曲线设计问题，利用MATLAB语言进行GUI编程，实现了对蜗线齿轮副节曲线的参数化设计。对其传动特性、凹凸性进行了分析，完成了齿轮副节曲线的动态模拟，提高了节曲线设计效率，为后续的设计和制造提供了便利。

蜗线齿轮 节曲线 MATLAB/GUI动态模拟

非圆齿轮作为一种特殊的传动机构，不但具有一般齿轮传动的优点，而且可以代替凸轮、连杆等非匀速传动机构，具有结构紧凑、运动精度高、传动平稳等特点［1,2］，因此，非圆齿轮的应用前景相当广阔。蜗线型齿轮是一种新型的非圆齿轮，它以蜗线作为齿轮节曲线的参数方程来设计，这种齿轮在机床往复运动机构、农用机械、纺织机械引纬机构、冶金行业连铸机等装置中，用来实现周期性往复运动，具有较高的使用价值［3］。

目前，根据已有资料来看［3-5］，蜗线齿轮虽有应用，但应用范围并不广泛，主要是由于蜗线齿轮的设计、计算较为复杂、加工成本较高所致。笔者利用MATLAB/ GUI编程技术设计蜗线齿轮副节曲线绘制系统，提高蜗线齿轮副节曲线设计的效率。

1 蜗线齿轮的数学模型

蜗线齿轮的极坐标方程为：

式中：b为发生圆直径；l为定长；φ1为主动轮1的极角，其节曲线如图1所示。

图1中，O1X为极坐标轴，O1为极坐标原点，O1O2为蜗线齿轮副的中心距，其长度为a，A为O1B和发生圆的交点，B在主动轮1的节曲线上；2为从动轮，φ2为从动轮的极角，C为O2C和从动轮2节曲线的交点。

▲图1 蜗线齿轮副节曲线

1.1 节曲线和传动比

对外啮合传动的非圆齿轮，若主动轮1的节曲线为蜗线，n1为主动轮1转动一周时，传动比变化的周期数（阶数），则其节曲线方程为：

若从动轮2的阶数为n2，则其节曲线方程为：

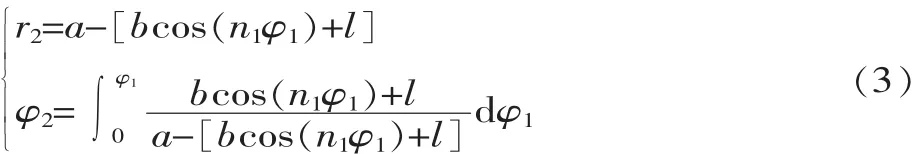
由于节曲线不是圆，其节曲线各点的曲率半径是不同的。根据微分几何，曲率半径ρ的计算公式为［6］：

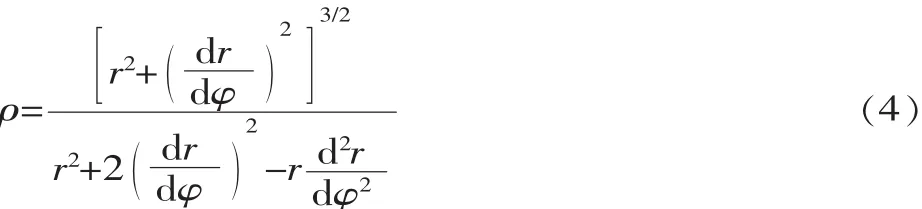
将主动轮1的节曲线方程（2）代入式（4），可得主动轮节曲线上各点的曲率半径ρ1为：

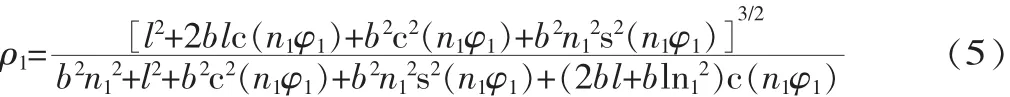
式中：c=cos；s=sin。

将从动轮2的节曲线方程（3）代入式（4），可得从动轮节曲线上各点的曲率半径ρ2为：

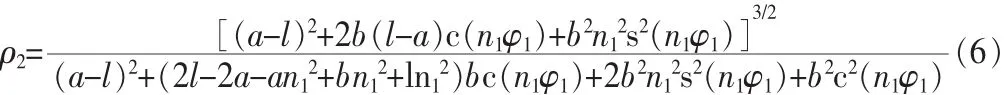
由于在实际应用中，非圆齿轮大多数应用场合都有封闭性要求，因此节曲线必须满足封闭性条件，从动轮2封闭的条件为：

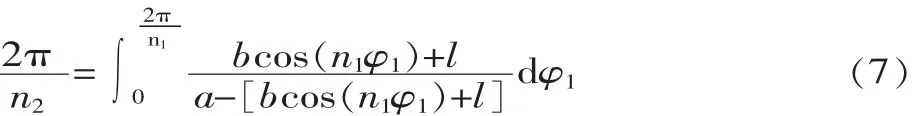
应用留数定理对式（7）进行计算，解得中心距为：

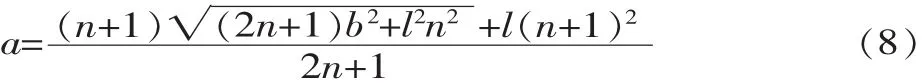
式中：n=n2/n1。

主、从动轮的传动比为：

主、动轮1的节曲线弧长为：

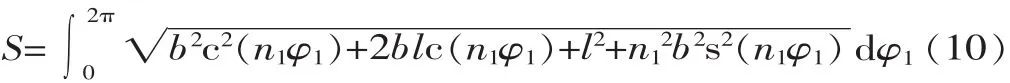
根据节曲线的封闭性和轮齿在节曲线上的均布性，其弧长还应满足下述条件：

式中：m为模数；z为齿数。

1.2 凹凸性分析

非圆齿轮的加工方法有多种，其节曲线的凹凸性对刀具及加工方案的选择有重要影响。当节曲线凹型时，只能选用线切割或适当直径的插齿刀插制，而不能用齿条型刀具或齿轮滚刀加工［6］，因此，设计非圆齿轮时需对其凹凸性进行校验。

2 节曲线参数化设计系统的实现

节曲线设计是蜗线齿轮副设计的关键，需满足凹凸性、封闭性等条件，其方程由主动轮齿数z1、模数m、中心距a，以及主、从动轮阶数n1和n2共同确定。在设计蜗线齿轮副节曲线时，需对各个设计参数反复调整、校验，计算量大。目前，虽有众多学者对常见非圆齿轮（如椭圆齿轮）的参数化设计问题作了大量研究，但针对蜗线齿轮副节曲线参数化设计却鲜有涉及。笔者设计的蜗线齿轮副节曲线参数化设计系统不仅能方便、快捷地对节曲线进行设计，而且能直观地反映节曲线形状及传动比曲线，系统设计流程如图2所示。

2.1 系统模板设计

模板设计是系统设计的基础，在设计模板时，首先需建立一个MATLAB/GUI模板文件，模板中按钮、文本框、标签、图轴等控件的选择由蜗线齿轮副节曲线设计所需的初始参数（z1、m、a、n1、n2）及输出参数（a、b、l）确定。其次，需对各控件的String及Name属性作必要修改，便于编程计算时快速、准确地调用相关函数。最后，按系统所要实现的功能，合理调整控件位置，使系统模板简洁、美观，设计的模板界面如图3所示。

▲图2 系统设计流程图

▲图3 系统模板图

2.2 函数设计与实现

图3中的图轴（jqx_axes、cdb_axes）中节曲线及其特性曲线的显示是由后台程序控制的，通过命令按钮“确定”来触发，为此，需将命令按钮和回调函数之间建立联系，其中 “确定”按钮的Tag属性为“pushbutton1”，在pushbutton1_Callback函数下添加代码，部分代码如下：

完成操作后单击“退出”按钮即可。

3 实例分析

为了验证上述GUI模板各模块功能的有效性，表1中给出蜗线齿轮副节曲线设计的两组数据A和B的设计参数。

通过凹凸性分析可知，并非任何设计参数都符合蜗线齿轮副节曲线的生成条件。如将表中A组数据输入系统时，单击“确定”按钮后，因不满足凹凸性条件，系统将弹出“节曲线参数有误，请重新输入！”的出错提示对话框。当输入B组数据后，满足设计要求，通过后台程序计算所得参数将显示在“输出参数”一侧，其运行效果如图4所示。

完成节曲线绘制后，利用save命令，将图中蜗线齿轮副节曲线保存为.jgp格式文件，将其导入CAXA软件的工作环境中便可进行齿轮齿廓设计。

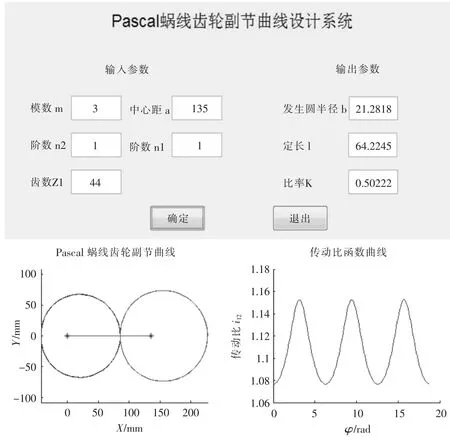
▲图4 蜗线齿轮副节曲线设计系统效果图

4 结束语

利用MATLAB软件的GUI编程功能，设计了蜗线齿轮副节曲线绘制平台，能在变参情况下快速完成蜗线齿轮副节曲线的绘制，显示节曲线啮合的动态效果，并生成相应传动比曲线，提高了蜗线齿轮副节曲线的设计效率。

［1］周娜,何丽,许纪晴.基于MATLAB的非圆齿轮节曲线设计［J］.机电产品开发与创新,2007,20（1）:7-8.

［2］刘永平,吴序堂,李鹤岐.常见的凸封闭节曲线非圆齿轮副设计［J］.农业机械学报,2007,38（6）:143-146.

［3］廖伟,赵匀,方明辉.巴斯噶蜗线齿轮在分插机构上的应用和参数优化［J］.浙江理工大学学报,2009,26（4）：547-550.

［4］任廷志,程爱明,景奉儒.蜗线齿轮及其共轭齿轮的几何分析与仿真［J］.机械工程学报,2006,42（9）:71-75.

［5］Bair BiingWen.Computer Aided Design of Elliptical Gears［J］.Journal of Mechanical Design,2002,124（6）:787-793.

［6］吴序堂,王贵海.非圆齿轮及非匀速比传动［M］.北京：机械工业出版社,1997.

［7］刘永平,孟鹏飞.巴斯噶蜗线型齿轮的啮合特性及数字制造技术研究［J］.制造技术与机床,2011（12）:90-93.

［8］兰红，田进，李淑芝，等.基于MATLAB GUI的图像处理平台设计［J］.江西理工大学学报，2014,35（3）：79-84.

（编辑 小 前）

In accordance with the theory of engagement of non-circular gear and aiming at the design issue involving pitch curve of worm gear pairs,MATLAB language was used for GUI programming and parametric design of the pitch curve of the worm gear pairs was realized.With analyses of the transmission characteristic and convexity and by dynamic simulation of the pitch curve of gear pairs it was possible to improve the design efficiency of pitch curve and facilitated subsequent designs and manufacturing.

Worm Gear Pitch Curve MATLAB/GUI Dynamic Simulation

TH132.424

A

1000-4998（2015）10-0033-03

*国家自然科学基金资助项目（编号：51265023）

2015年4月