基于联合卡尔曼滤波算法的智能铲运机组合定位导航分析*

□姜勇

北京矿冶研究总院 北京 100160

基于联合卡尔曼滤波算法的智能铲运机组合定位导航分析*

□姜勇

北京矿冶研究总院 北京 100160

以智能铲运机为研究对象，将航迹推算系统和激光测距识别系统数据同时作用于定位解的求解过程中，提出了一种基于联合卡尔曼滤波技术的智能铲运机组合定位导航分析方法，并进行仿真分析。结果表明，该算法可以有效地减小组合系统的定位误差，提高系统的定位精度。

智能铲运机 卡尔曼滤波 组合定位导航

卡尔曼滤波技术是对随机信号作估计的算法之一，它在滤波技术中引入现代控制理论中状态空间的概念，系统用状态方程来描述，采用递推计算的方法，不需要了解过去时刻的测量值，只需根据前一时刻的估计值和当前时刻的测量值，即可递推计算出当前时刻的估计值，并且可以在一定的条件下给出无偏估计量，能够很好解决多维非平稳随机过程的估计问题［1，2,3］。笔者应用联合卡尔曼滤波技术对智能铲运机的组合定位导航算法进行研究，将航迹推算系统和激光测距识别系统数据同时作用于定位解的求解过程中，根据两个系统的数据质量，自适应调节两个系统在定位解中的作用，实现了航迹推算和激光测距识别组合定位导航系统定位信息的最优融合。

1 联合卡尔曼滤波算法

联合卡尔曼滤波器是一种特殊的分散卡尔曼滤波器，与分散卡尔曼滤波器不同的是，联合卡尔曼滤波器包含一个信息分配过程，在此过程中，基于理论上的信息分配原理，主滤波器中的动态信息被分配到每一个局部滤波器中［4］。

1.1 各滤波器估计不相关条件下的联合卡尔曼滤波算法

假设各子滤波器的估计独立，对两个局部滤波器（N=2）设局部估计状态为，相应的估计误差方差为P11和P22。考虑融合后的全局状态估计为局部状态估计的线性组合，即：

式中：W1、W2为待定加权矩阵。

式中：X为真实状态。

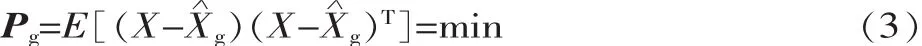
由以上假设条件可以推出：

利用数学归纳法，将以上结果推广到N个局部状态估计，得：

1.2 各滤波器估计相关条件下的联合卡尔曼滤波算法

在一般情况下各滤波器是相关的。可以采用方差上界技术对滤波过程进行适当改造，使局部滤波估计实际上不相关。设各子滤波器的状态估计表示如下：

假设将系统过程噪声总的信息量分配到各个局部滤波器和主滤波器中，即:

根据信息守恒原理，由上式可知：

状态估计初始信息P0-1也可按照上述方法分配。假设状态估计的信息可同样分配，即：

2 基于联合卡尔曼滤波的组合定位导航算法

智能铲运机在地下巷道内完成自主导航行走，主要靠检测巷道壁的环境信息并结合巷道电子地图进行匹配，系统通过多传感器的信息融合及联合卡尔曼滤波算法对铲运机的状态进行估计，并对铲运机的行驶进行指导。图1所示为智能铲运机信息融合定位算法图。

航迹推算/激光测距识别组合定位导航的联合卡尔曼滤波器结构设计如图2所示，组合系统由航迹推算子系统、基于激光测距识别子系统和主滤波器三部分组成，两个子系统各有一个局部卡尔曼滤波器，用来处理航迹推算系统和激光测距/识别系统的检测数据。子系统的局部状态估计Xd、Xj和估计误差协方差矩阵Pd、Pj输入到主滤波器，主滤波器对局部滤波器的信息进行分析融合，并输出整个系统的最优估计Xg、Pg，同时根据信息分配因子λ1、λ2对局部滤波器进行反馈重置，作为下一时刻迭代运算的初始值，从而提高了局部滤波器状态估计的精度。

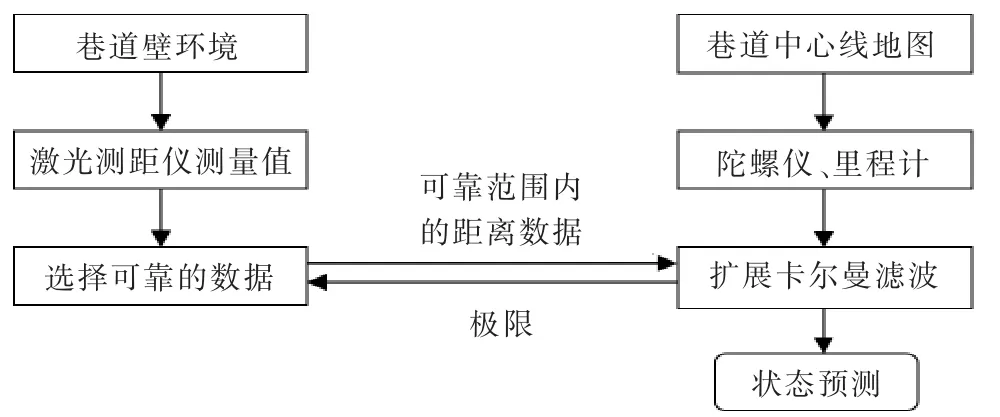
▲图1 信息融合定位算法框图

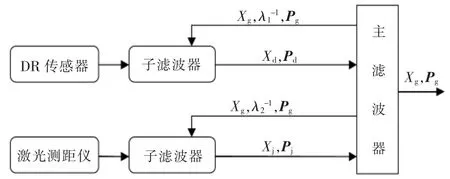
▲图2 航迹推算/激光测距识别组合定位导航的联合卡尔曼滤波器结构

3 组合定位导航算法仿真分析

为了验证航迹推算和激光测距/路标识别组合定位导航算法，采用计算机仿真的方法分别仿真车辆的真实行驶路线数据，航迹推算系统定位数据和激光测距/识别系统定位数据，然后利用这些仿真数据来对组合定位导航算法的性能进行分析［5～7］。图3和图4分别给出了航迹推算定位系统和激光测距识别定位系统单独定位的铲运机横向位移误差曲线，图5是由组合定位系统定位的铲运机横向位移误差曲线。

为了进一步缩小组合导航系统的定位误差，提高定位精度，使铲运机的控制更加准确，行驶路线更加合理，不出现前面实验中出现的非正常的转向振动。笔者

对组合导航系统采用联合卡尔曼滤波算法进行了系统仿真。图6是智能铲运机经过联合卡尔曼滤波后系统的位置估计图。

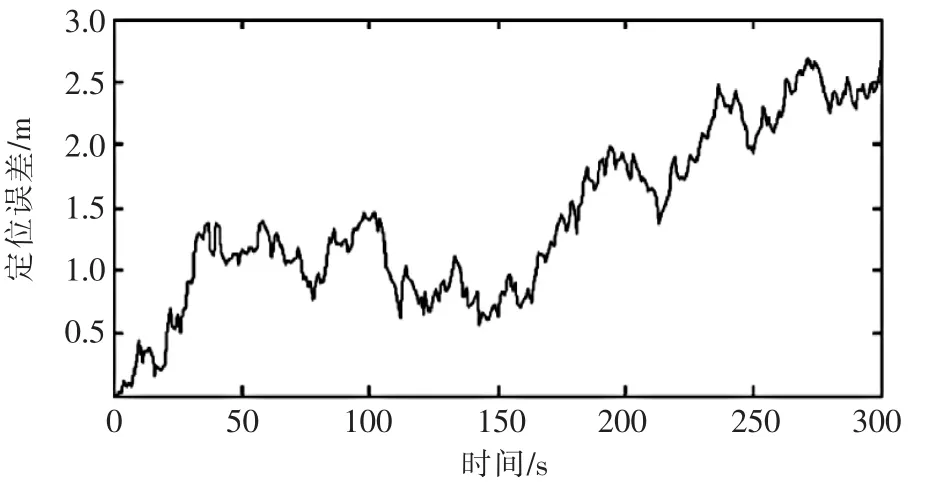
▲图3 航迹推算横向定位误差

▲图4 激光测距识别横向定位误差

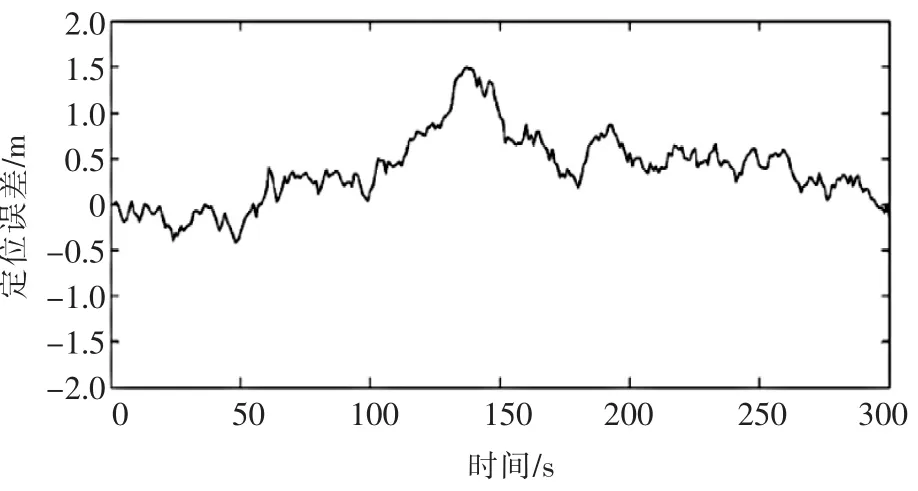
▲图5 组合定位横向定位误差

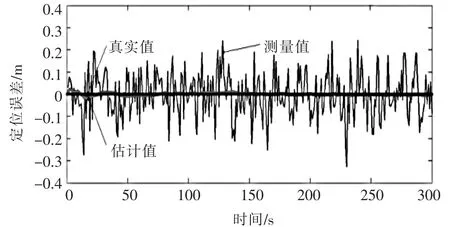
▲图6 联合卡尔曼滤波后智能铲运机的横向位置估计

4 结论

（1）单独的航迹推算定位或者激光测距识别定位的定位误差都相对较大，通过对航迹推算和激光测距识别定位系统进行组合定位后，其定位误差明显减小，误差波动更加平滑，定位精度得到了显著提高。

（2）卡尔曼滤波器能够有效地在比较大的干扰下对真实值做出很好的估计，即使观测端加入干扰较大时（如巷道壁出现很不规则的情况），卡尔曼滤波器依然可以比较有效地进行滤波，并对铲运机的状态做出比较准确的估计。采用联合卡尔曼滤波算法可以有效地减小组合系统的定位误差，提高系统的定位精度。

［1］盛三元，王建华.基于多传感器信息融合技术的联合卡尔曼滤波器的设计及应用［J］.情报指挥控制系统与仿真技术，2002（2）：53-58.

［2］付梦印，邓志红，闫莉萍.Kalman滤波理论及其在导航系统中的应用（第二版）［M］.北京：科学出版社，2010.

［3］邓自立.最优滤波理论及其应用［M］.哈尔滨：哈尔滨工业大学出版社，2000.

［4］陈则王，袁信.联合卡尔曼滤波在车辆组合导航系统中的应用［J］.重庆大学学报（自然科学版），2005，28（10）：86-90.

［5］张葛祥，李娜.MATLAB仿真技术与应用［M］.北京：清华大学出版社，2003.

［6］Joseph Nsasi Bakambu，Vladimir Polotski.Autonomous System for Navigation and Surveying in Underground Mines［J］.Journal of Field Robotics,2007,24（10）：829-847.

［7］H Martinez Barbera,D Herrero Perez.Autonomous Navigation of an Automated Guided Vehicle in Industrial Environments［J］.Robotics and Computer-Integrated Manufacturing，2010,26（4）:296-311.

（编辑 小 前）

TH123

A

1000-4998（2015）10-0036-03

*国家863高技术研究发展计划项目（编号：2011AA060403）

2015年4月