一种基于相位补偿的前向散射阴影逆合成孔径雷达快速成像方法

刘长江 胡 程② 曾 涛② 周 超



一种基于相位补偿的前向散射阴影逆合成孔径雷达快速成像方法

刘长江①胡 程*①②曾 涛①②周 超①

①(北京理工大学信息与电子学院 北京 100081)②(北京理工大学嵌入式实时信息处理技术北京市重点实验室 北京 100081)

传统的基于菲涅尔数值积分的前向散射阴影逆合成孔径雷达(SISAR)成像计算复杂且运算量较大。为提高运算速度，该文对SISAR快速成像方法进行了研究。首先提出一种基于快速傅里叶变换(FFT)的SISAR快速成像方法，并给出了FFT引入相位误差的补偿公式；随后通过对运动补偿后信号频谱进行分析给出了SISAR成像的采样准则，其指出成像所需的信号采样率可以远小于奈奎斯特采样率。仿真结果表明，利用FFT和低采样率的快速成像方法可以在精确成像的基础上大大降低运算量，具有实际工程意义。

前向散射雷达；阴影逆合成孔径雷达；快速傅里叶变换；相位补偿；奈奎斯特采样率

1 引言

作为双基地雷达的一个特例，前向散射雷达的特点是双基地角在附近[1]。通常而言，目标在前向散射配置下的雷达散射截面积远大于单基地配置下的雷达散射截面积，而且与目标的表面材质无关，因此前向散射雷达具有探测隐身目标的潜力[2]，在进入21世纪以来已经逐步成为新体制雷达的一个热点研究方向。许多公开研究已经成功将前向散射雷达应用于空中目标探测[3]，海面预警[4,5]以及地面目标识别等方面。作为前向散射雷达目标识别的重要手段，阴影逆合成孔径雷达(Shadow Inverse SAR, SISAR)成像理论由Chapurskiy等人[10,11]发展于20世纪80年代末期，并于2000年的IEEE雷达会议上得到了更多的关注[12]。现有的SISAR成像算法主要分为小衍射角SISAR成像算法和大衍射角SISAR成像算法。其中小衍射角SISAR算法最先被提出，且易于运动补偿和工程实现；大衍射角SISAR算法出现较晚，虽然成像效果更好但工程实现较为困难。本文主要针对小衍射角SISAR成像算法进行讨论。

根据SISAR理论，在菲涅尔区目标的前向散射回波信号可以表示为目标复轮廓函数(Complex Profile Function, CPF)的菲涅尔变换[10]，而目标的侧影轮廓信息可以从CPF中提取。一般而言，菲涅尔变换的计算可以通过直接数值积分实现，但这样算法复杂且对运算量要求较大。当采样点较多且需要通过搜索进行参数估计[13]时，对运算量的需求就显得更加重要。而在前向散射雷达系统组网化、小型化和低功耗化的发展趋势下，寻求一种简便有效的SISAR计算方法来进行自动信号处理变得十分迫切。

实际上，SISAR成像等效于对多普勒相位补偿后的回波进行傅里叶变换[11]，因此如果将快速傅里叶变换(FFT)应用到SISAR成像的数值计算中可以大大提高运算速度。文献[13]和文献[14]都给出了基于连续傅里叶变换的SISAR成像公式，但并没有给出利用FFT进行离散化计算的具体方法，同时都没有给出中线像的恢复结果。文献[11]指出当目标高度较高时，由CPF模值得到的高度差像会产生较严重的畸变，但由CPF相位得到的中线像则不会出现畸变。这说明中线像是在目标高度较高时的唯一识别手段。实际仿真发现，直接利用FFT计算得到的CPF在奇偶分辨单元会出现近似为的相位误差，因此必须进行相位补偿。

为解决上述问题，本文在对基于FFT的SISAR数值计算方法进行详细阐述的基础上，对成像结果出现相位误差的原因进行了具体分析，并给出了一种精确的相位补偿方法。利用提出的快速成像方法，可以在精确恢复目标高度差像和中线像的同时大大降低运算量。随后利用多普勒补偿后前向散射回波信号的频谱特性，给出了SISAR成像的信号采样定理。定理表明可以以远低于多普勒谱宽的采样率进行目标前向散射回波信号的采样而不影响SISAR成像的效果，这从另一方面进一步提高了SISAR成像的计算速度。本文结构安排如下：第2节简要介绍了SISAR成像的基本原理；第3节首先给出了基于FFT和相位补偿的SISAR成像方法，随后推导得出了相关采样准则；第4节通过仿真验证了方法的有效性；第5节是结束语。

2 SISAR成像基本原理

前向散射雷达系统拓扑结构如图1所示。

图1 前向散射雷达系统拓扑

3 SISAR快速成像

菲涅尔变换是广义变换集合中的一类，这类变换集合通常称为线性正则变换或二次相位变换。这类变换集合的子集通常可以化成一些系列连续的简单操作，如线性调频信号相乘，线性调频信号卷积，尺度变换以及普通的傅里叶变换。这里，我们要讨论一种SISAR成像的分解数值计算方法，其核心部分是FFT，但由于中线像提取要求算法具有保相性，因此必须详细分析算法对相位的影响。

3.1 SISAR成像的FFT实现

从式(3)中可以明显看出SISAR积分可以理解为回波信号与二次相位因子乘积的傅里叶变换的形式[13]，而将变换结果与一个二次相位因子和一个常数项相乘即可以得到目标的CPF。也就是说，如果将看作是待变换的信号，将看作是傅里叶变换的核函数，那么式(3)可以通过离散傅里叶变换(DFT)实现。假设信号在时域的采样点数为，回波时间的离散坐标可以写为

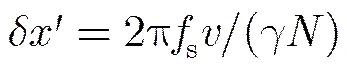
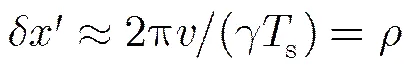
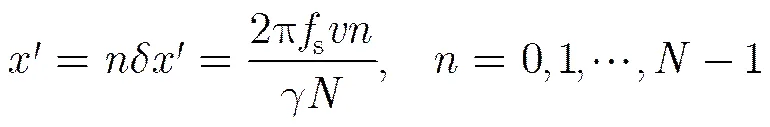
考虑进行频谱搬移将零频置于频谱中心，这样式(10)可以重写为

将式(11)代入，即可得到式(5)中DFT左侧二次相位因子的离散表达式：

式(5)中的DFT操作可以通过FFT实现，这样可以将运算量从降低到。这样我们分别给出了使用FFT进行SISAR快速成像的计算公式和成像域坐标表达式。

3.2 SISAR成像的相位补偿

虽然式(5)~式(12)的推导是精确的，但实际使用FFT进行数值计算却会在某些成像点出现模值近似为的相位误差。出现这种问题的原因是FFT本身默认输入信号的初始相位是第1个采样点的相位，而不是我们期望的时刻的相位。如果强制设定信号的第1个点是零时刻，这样虽然不会出现相位误差，但根据式(6)，由于时移的性质恢复目标像会严重偏离成像域的中心位置，甚至可能会被割裂在成像域的两侧，而且当有编队目标出现时，目标像的前后顺序可能不符合其真实出现顺序，从而不利于观察。因此这里给出一种精确的相位误差补偿方法。

将式(11)代入，式(13)可以重写为

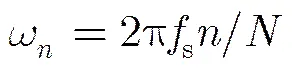
图2 SISAR成像流程图

3.3 SISAR成像的采样准则

根据传统的奈奎斯特采样准则，对前向散射回波信号一类的低通信号，应当至少以两倍最高频率进行采样，否则将会出现频谱混叠。但由于基于FFT的SISAR成像中并不是回波信号直接作FFT，而是对多普勒补偿后的回波作FFT，显然补偿后信号的频域特性与补偿前有很大不同，因此我们可以考虑从补偿后信号的频谱特性入手，推导新的采样准则。假设目标在成像域占据个分辨单元，则根据式(14)，对CPF即有

4 仿真分析

为了验证前面给出的快速成像方法及采样准则的有效性，下面给出仿真实例。仿真中假设目标模型为简单的飞机侧影轮廓，如图3所示。

图3 目标模型示意图

图4(a)和图4(b)分别给出了使用基于FFT的快速成像方法和传统的菲涅尔数值积分法[12]恢复得到的目标高度差像和中线像。结果表明，在未经过相位补偿时，FFT的默认操作导致重构CPF在奇数个分辨单元存在近似为的相位误差。值得注意的是，这种误差在飞机尾翼处的分辨单元出现了相位缠绕，受目标轮廓起伏以及噪声的影响，这种相位缠绕很容易发生，仅仅通过奇偶分辨单元的判别进行补偿是不可行的。而按照本文给出的相位补偿公式进行补偿，可以完全消除FFT默认操作带来的影响，得到的精确的CPF相位，并以此精确恢复目标高度差像和中线像，其结果与传统菲涅尔数值积分法得到的成像结果基本一致，验证了快速成像的有效性。

图4 SISAR成像结果对比

下面考察用低于奈奎斯特采样率采样的信号进行SISAR成像的效果。对前面给定参数，按照多普勒谱宽计算得到的最低采样率约为，而按照式(20)计算得到的最低采样率约为，为了保证足够的成像区域及尽量消除离散化引起的位置平移，我们令，仿真得到的成像结果如图5所示。结果表明，即使回波信号采样率远低于奈奎斯特采样率，无论使用传统积分计算还是FFT快速计算，都获得了很好的SISAR成像结果。根据式(9)计算得到的成像区域宽度约为，也与图5(a)中结果一致，这说明一般情况下，当使用小于奈奎斯特采样率的采样的信号进行成像时，受影响的仅是成像区域的范围。

由于中线高度像是利用相位提取，而通常相位比幅度更容易受噪声影响，因此下面将通过仿真来分析所提出算法对噪声的敏感性。考虑到前向散射回波幅度受RCS影响而起伏明显，因此定义峰值信噪比为接收回波峰值功率与噪声功率之比。

5 结束语

本文给出了一种基于FFT和相位补偿的SISAR快速成像方法，根据理论推导，分析了引起相位误差的原因，并给出了相位误差的精确补偿公式，使用该补偿公式可以精确恢复目标中线像。进一步地，利用运动补偿后回波信号的频谱特性，给出了SISAR成像的采样准则，其表明SISAR成像所需的回波信号采样率不再取决于信号多普勒带宽，而取决于目标长度及分辨率，因此可以对以远小于奈奎斯特采样率采样的信号进行SISAR成像。仿真结果验证了本文提出的快速成像算法的有效性和快速性，同时也表明该方法在噪声存在的条件下依然适用，因此其具有实际的工程意义。

图5 低采样SISAR成像结果           图6 噪声对成像的影响

[1] Glaser J I. Bistatic RCS of complex targets in forward scatter[J]., 1985, 21(1): 70-78.

[2] Glaser J I. Some results in the bistatic radar cross section (RCS) of complex objects[J]., 1989, 77(5): 639-648.

[3] Suberviola I, Mayordomo I, and Mendizabal J. Experimental results of air target detection with a GPS forward scattering radar[J]., 2012, 9(1): 47-51.

[4] Gashinova M, Daniel L, Sizov V,.. Phenomenology of Doppler forward scatter radar for surface targets observation [J].,&, 2013, 7(4): 422-432.

[5] Kabakchiev C, Behar V, Garvanov I,..Detection, parametric imaging and classification of very small marine targets emerged in heavy sea clutter utilizing GPS-based Forward Scattering Radar[C].2014 IEEE International Conference on Acoustics, Speech and Signal Processing, Florence, Italy, 2014:793-797.

[6] Abdullah N F, Rashid N E A, Othman K A,.. Vehicles classification using Z-score and modelling neural network for forward scattering radar[C]. Proceedings of 15th International Radar Symposium, Lviv, Ukraine, 2014:1-4.

[7] Cheng Hu, Sizov V, Antoniou M,.. Optimal signal processing in ground-based forward scatter micro radars[J]., 2012, 48(4): 3006-3026.

[8] Hu Cheng, Zhou Chao, Zhu Can-yan,.. Forward scatter radar SISAR imaging: theory and primary experimental results analysis[C]. Proceedings of 14th International Radar Symposium, Dresden, Germany, 2013:643-648.

[9] Hu Cheng, Zhou Chao, Zeng Tao,.. Radio holography signal reconstruction and shadow inverse synthetic aperture radar imaging in ground-based forward scatter radar: theory and experimental results[J].,&, 2014, 8(8): 907-916.

[10] Chapurskiy V V. Image construction from one-dimensional radioholograms synthesized at small angles of diffraction[J]., 1988, 33: 1747-1756.

[11] Surikov B S, Khasina E S, and Chapurskiy V V. Correlation and spectral functions of one-dimensional radio holograms synthesized at small diffraction angles[J]., 1989, XXXIY: 409-419.

[12] Chapurskiy V V and Sablin V N. SISAR: shadow inverse synthetic aperture radiolocation[C]. The Record of the IEEE 2000 International Radar Conference, Washington DC, USA, 2000: 322-328.

[13] Luo Ying, Hu Dong-liang, Luo Bin-feng,. Motion compensation for SISAR based on contrast maximization[C]. 1st Asian and Pacific Conference on Synthetic Aperture Radar, Huangshan, China, 2007: 431-434.

[14] Cao Yun-he, Zhang Tao, Luo Bin-feng,.. Experimental results for shadow inverse synthetic aperture radar[C]. Proceedings of 2009 IET Radar Conference, Guilin, China, 2009: 1-3.

[15] Zeng Tao, Li Xiao-liang, and Hu Cheng. Investigation on accurate signal modeling and imaging of the moving target in ground-based forward scatter radar[J].,&, 2011, 5(8): 862-870.

[16] Hu Cheng, Li Xiao-liang, Long Teng,.. An accurate SISAR imaging method of ground moving target in forward scatter radar[J]., 2012, 55(10): 2269-2280.

[17] Liu Chang-jiang, Hu Cheng, Xu Jia,.. Modified signal modeling and imaging method of non-perpendicular crossing targets in forward scatter radar[C]. Proceedings of 2014 IEEE Radar Conference, Cincinnati, USA, 2014: 291-295.

Fast Forward Scatter Shadow Inverse Synthetic Aperture RadarImaging Algorithm Based on Phase Compensation

Liu Chang-jiang①Hu Cheng①②Zeng Tao①②Zhou Chao①

①(,,100081,)②(-,,100081,)

The numerical calculation of forward scatter Shadow Inverse Synthetic Aperture Radar (SISAR) imaging is usually performed by the Fresnel numerical integral which is complicated and time consuming. To improve the calculation speed, the fast SISAR imaging method is investigated. Firstly, a fast imaging method based on the Fast Fourier Transform (FFT) is proposed while the phase errors introduced by the FFT are compensated. Then, through the analysis of the spectrum on the motion compensated signal, the sampling law for SISAR imaging is given, indicating that signals used for imaging can be sampled at a rate much lower than the Nyquist sampling rate. Simulation results show that the proposed fast imaging method can give accurate profiles and significantly reduce the computation, which is of practical meaning in engineering application.

Forward scatter radar; Shadow Inverse Synthetic Aperture Radar (SISAR); Fast Fourier Transform (FFT); Phase compensation; Nyquist sampling rate

TN957.52

A

1009-5896(2015)10-2294-06

10.11999/JEIT141576

2014-12-10；改回日期：2015-05-29；

2015-07-17

胡程 hucheng.bit@gmail.com

国家自然科学基金(61172177)和长江学者计划(T2012122)

The National Natural Science Foundation of China (61172177); The Program for Changjiang Scholars (T2012122)

刘长江： 男，1990年生，博士生，研究方向为前向散射雷达及昆虫雷达.

胡 程： 男，1981年生，教授，主要从事GEO SAR、双基地SAR及前向散射雷达等方面的研究.

曾 涛： 男，1971年生，教授，主要从事雷达系统及雷达信号处理等方面的研究.