城市轨道交通大客流等车时间计算模型

曹志超，袁振洲，张思林，吴昊灵

(北京交通大学城市交通复杂系统理论与技术教育部重点实验室，北京 100044)

城市轨道交通大客流等车时间计算模型

曹志超，袁振洲，张思林，吴昊灵

(北京交通大学城市交通复杂系统理论与技术教育部重点实验室，北京 100044)

城市轨道交通的运营在早、晚高峰或突发大客流情况下，客流量超过列车最大承载能力，乘客将排队等待后继车辆而延长等车时间。乘客等车时间是评价交通服务水平和优化列车开行方案的关键因素。提出一种基于列车时刻表，利用排队论方法，准确计算严重拥挤情况下乘客等待时间的模型。针对乘客等车时间计算模糊的问题，在考虑乘客实时到达规律、OD(起讫点)分布、发车间隔和列车运能的基础上，创新地提出可用于城市轨道交通网络和双向的大客流和常规客流的等车时间累计计算方法，可为大客流的时刻表优化策略提供理论依据，并通过累计输入-输出算法计算大客流等车时间的实例，分析多参数变化趋势。实证表明，模型可用于城市轨道交通网络和双向的大客流和常规客流的等车时间实时计算。

城市轨道交通；大客流；等车时间；列车时刻表

1 概述

城市轨道交通大客流集散效应为运管管理部门提出了严峻的考验，大客流最直接的表现为乘客等车时间延长，造成乘车延误。乘客在车站的等车时间已经成为评价车站服务水平的关键因素[1]。准确合理的计算乘客的等车时间可以优化城市轨道交通列车时刻表编制，把握乘客集散规律，对车站容纳能力、设备设施的评估都有很好的借鉴意义。尤其是车站大客流发生时，计算乘客的等车时间将成为理清列车延误和传播规律最直接有效的方法。结合列车开行方案理论，考虑乘客排队类型、供需动态平衡和列车运能等因素情况下，提出了一种系统化计算城市轨道交通大客流等车时间的计算方法。

国内学者对城市轨道交通乘客等车时间系统详尽的研究成果相对较少。文献[2] 通过调查建立了乘客等车时间满意度模型，定量评估了城市轨道交通突发大客流应急策略的优劣。非拥挤情况下，对短发车间隔的公共交通，传统的乘客平均等车时间取值为发车间隔时间的一半(Osuna and Newell， 1972; Welding， 1957)[3，4]。国外学者建立了流体动力学模型仿真乘客上车规律，计算了乘客总体等待时间用于优化列车调度和开行方案，如Newell (1971)[5]、 Osana and Newell (1972)[3]， 和 Hurdle (1973)[7]。Daganzo (1997)[8]提出了一种在常规开行方案下，拥挤乘客积累排队的计算方法，同时简化仿真了带有时间戳的乘客延误过程。

近期理论一般将乘客等车时间运用于发展周期列车时间表和平行运行图的优化模型。Zhou和Zhong[9，10]提出了广义资源限制的开行方案优化模型，利用分支定界算法计算了总等车时间和在途时间最小的时刻表。Liebchen (2008)[11]提出了完善图模型(well-established graph model)，优化了柏林列车时刻表，缩短了乘客在换乘和车站的等车时间。

就研究现状而言，拥挤情况下乘客等车时间的计算是基于时间戳的OD客流量和列车时间表的综合模型。AFCS (automatic fare collection systems)[12]已经较为成熟且广泛应用于乘客路径辨识、进出站时间记录等乘客行为的分析，同时也可作为本文基础数据来源。国内城市轨道交通大客流研究多集中于应用SIR模型的抽象仿真[2]，但由于模型本身的一些弊端，对客流时间规律的发掘不足。

本文基于城市轨道交通早晚高峰或赛事活动引发大客流情景下，严格按照列车时刻表，应用行人交通流排队论方法探索延误机理，针对多个站台不同的乘客拥挤延误区间构成，提出了系统化的城市轨道交通大客流等车时间计算模型，根据AFCS提供历史OD数据，应用累计输入输出方法，推演了乘客等车时间的实例。

2 等车延误机理

大客流拥挤延误机理在文献[2]中已有说明，即持续到达客流与每班列车剩余运能之间的矛盾问题。大客流拥挤延误其本质为排队延误，排队产生的最根本原因为周期性服务台的服务能力小于乘客到达率。地铁车站站台乘客排队上下车行为属于文献[12]排队类型中的C类，见图1，北京地铁车站正常上下车行为调研、仿真研究在文献[6]中已有详细阐述。

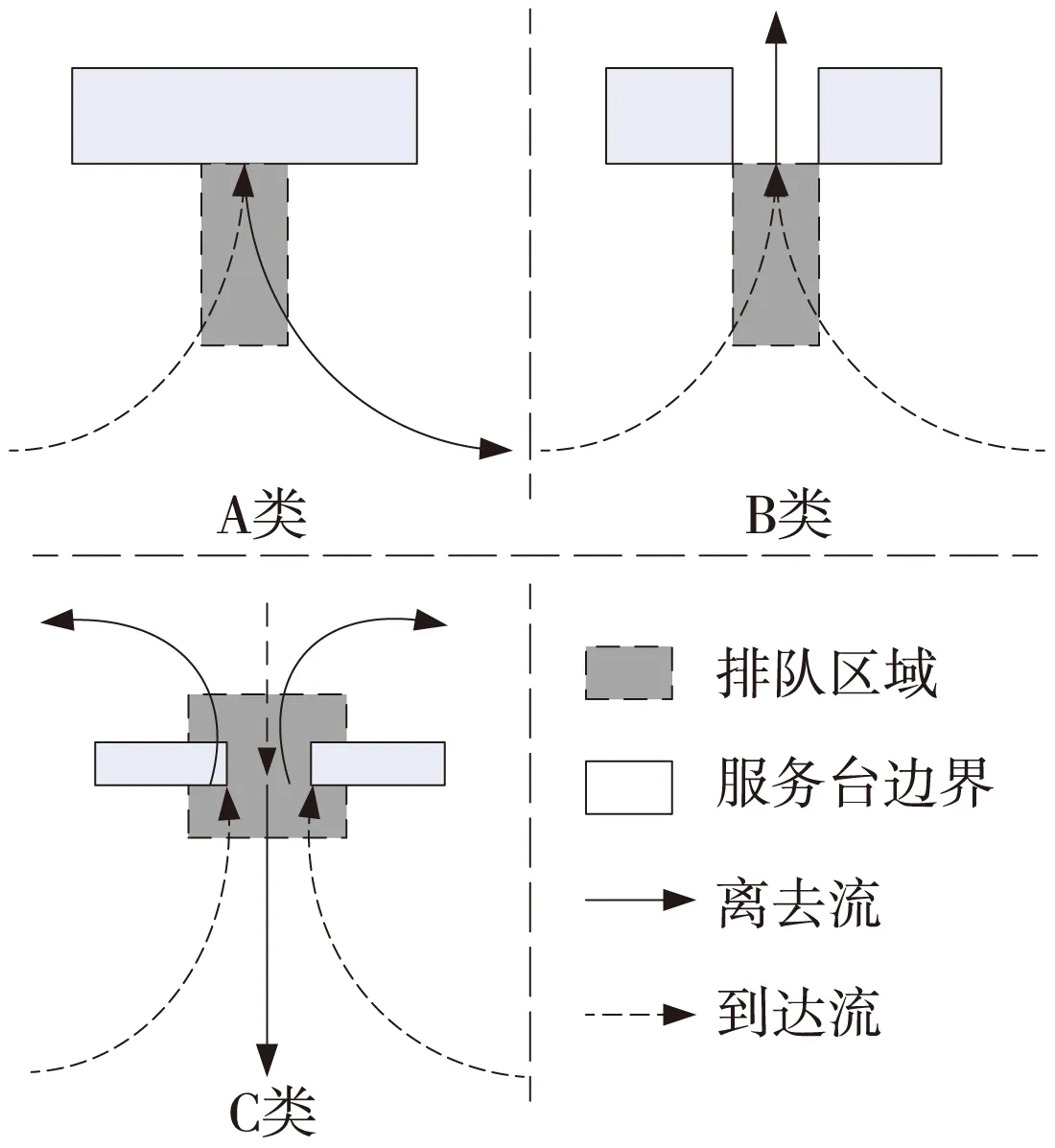
图1 排队类型

城市轨道交通列车提供周期性服务，大客流会导致队列靠后部分的乘客不能上车，滞留乘客等车时间必然将超过一个发车间隔，进而继续等待下i(i=1，2，…，N)班列车，相继等车延误机理如图2所示。

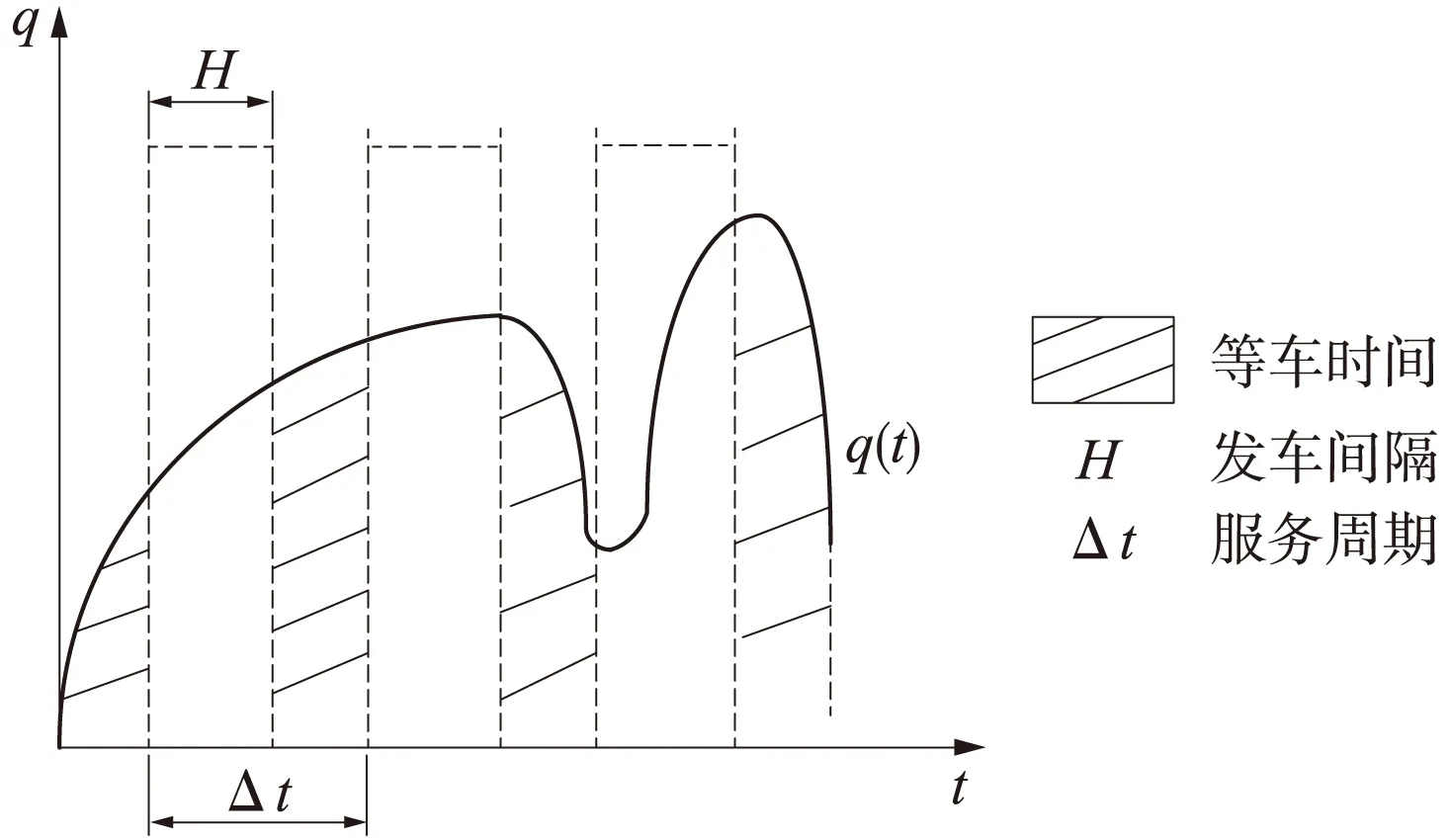
图2 等车延误机理

从图2中可以看出，等车延误机理可以由客流到达率λ(t)，流量函数q(t)，发车间隔H，服务周期Δt表示。在一个服务周期内，i车j站的等车延误的乘客人数为

(1)

式中，客流到达率λ(t)可根据不同车站具体情况假定Poisson分布或均匀分布，其参数标定可根据不同时间段内客流到达规律具体计算，如双峰型、平峰型等。流量函数q(t)的标定方法可参考文献[6]和文献[15-16]。

列车的停车时间tij，d表示为

(2)

公共交通运营时间内，乘客总等车延误人数D为

(3)

3 等车时间计算模型

在理清等车延误机理后，我们发现等车延误与列车时刻表、车内乘客的动态变化、发车间隔、车站乘客到达规律等参数难以建立直接关系。面对等车时间计算模糊的问题，提出了既适用于大客流又可计算日常情形下乘客等车时间的计算方法。

3.1 基本假设

对于j(j∈{1，2，…，N})车站，所有的乘客上车均符合一进一出的顺序排队原则(First-In-First-Out (FIFO) principle)[14]。FIFO原则需要针对两种情形分别说明：(1)对于平峰客流量，车站等车乘客都可以全部上车，无滞留乘客，那么乘客总的等车时间为列车离开时间减去乘客到达时间的差值总和。即使不遵循FIFO原则，所有乘客的等车时间都不会超过一个发车间隔。(2)对于早晚高峰或者大客流发生时，乘客经常需要等待i(i≥2)班列车才能上车。在实际情况中，早到乘客将有更多机会和优先权上车，同时这也符合排队论的先到先服务的原则。如果没有此假设，准确定位乘客上车顺序是极度复杂的，在微观层面，每个人的等车时间将难以刻画，这样大客流等车时间模型的计算误差将会大大失衡。

3.2 模型参数

城市轨道交通网络G，线路l，及列车时刻表等模型参数具体阐释见表1。

表1 模型参数

3.3 计算公式

模型中的重要参数已经在列表中释义，需要指出的是本模型中列车实际运行状况严格按照列车时刻表开行；停车间隔采用固定停车间隔，反驳文献[13]的“停站时间取决于上车速率和列车容纳能力”的说法；因简单明确的需要，列车容纳能力C在系统模型中为固定值，不能出现满载率大于100%的状态[2]。

列车i的到达时间为

(4)

这里，列车的运行时间rj包括站间距开行时间，启动加速和到站减速时间。其中，列车i的出发时间为

(5)

列车i与列车i-1的发车间隔为

(6)

车站j的等车客流量为

(7)

式中，车站j的滞留客流量和到达率可表示为

(8)

上车人数Bi，j为

(9)

式中，车站j的等车客流量又可表示OD量累计的形式

(10)

为了更好的简明表示，令∂，β，δ代表判断公式如下

(11)

(12)

(13)

滞留延误乘客人数Li，j为

(14)

在i站等待j车的乘客的等车时间TWi，j为

(15)

城市轨道交通乘客总等车时间Z是关于发车间隔Hi，j和列车载客能力C的函数，如式(16)所示

(16)

4 案例分析

4.1 计算

图3 城轨线抽象图

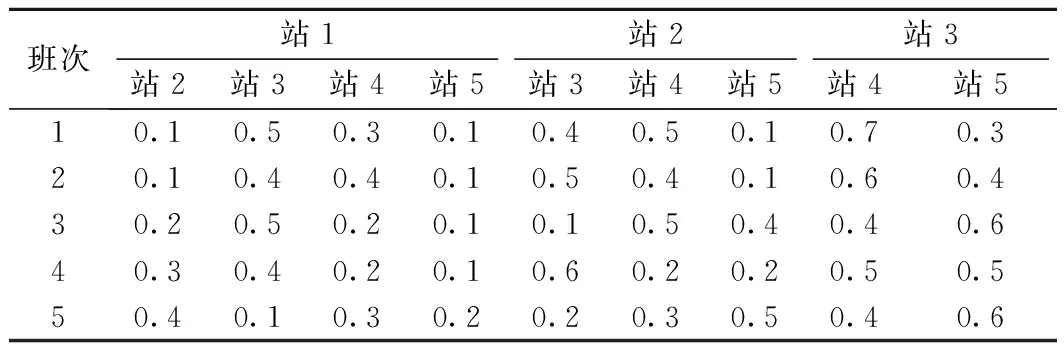
班次站1站2站3站2站3站4站5站3站4站5站4站510.10.50.30.10.40.50.10.70.320.10.40.40.10.50.40.10.60.430.20.50.20.10.10.50.40.40.640.30.40.20.10.60.20.20.50.550.40.10.30.20.20.30.50.40.6

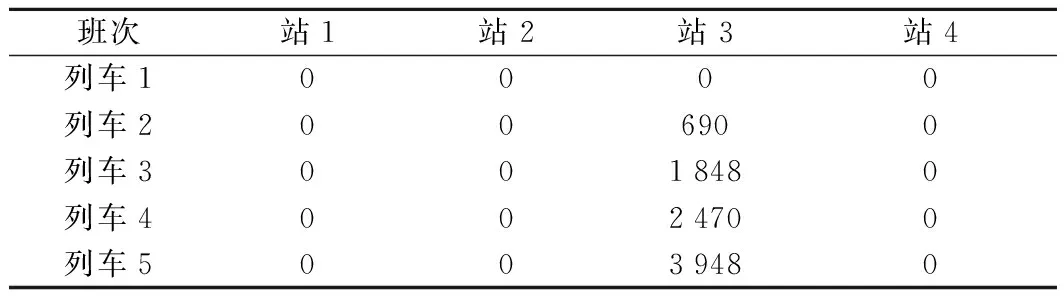
表3 各班列车延误乘客人数 人

注：延误乘客的含义为列车发车时到达车站站台，但由于拥挤未能上车的乘客。

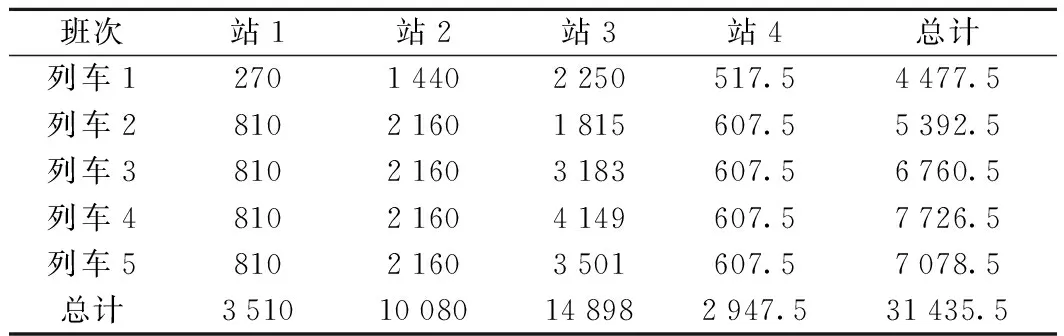
表4 各班列车上车乘客等车时间 min

4.2 灵敏度分析

从实际角度利用模型对乘客等车时间进行推演。发车间隔的改变是从列车时刻表的角度对大客流进行疏导，而不同的列车(A型车、B型车或轻轨等)运能则是从规划角度对大客流问题一种缓解措施。基于具体参变量变化和双因素(发车间隔与列车运能)联合分析结果如表5所示。

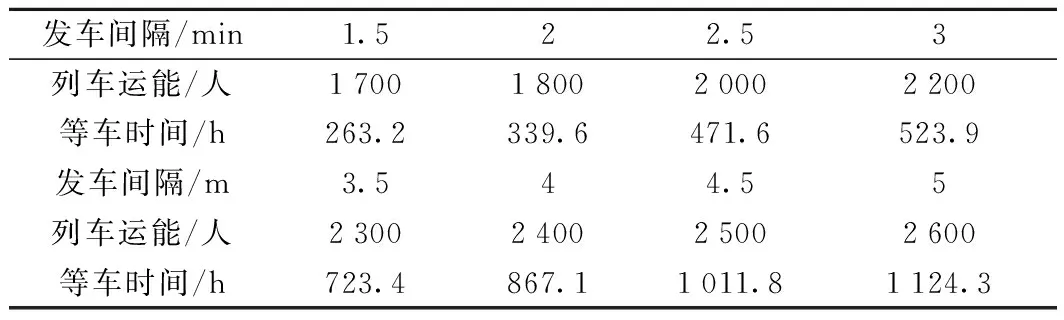
表5 双因素联合的灵敏度分析

城市轨道交通乘客等车时间的变化趋势与发车间隔和运能的综合关系是一个动态均衡匹配的问题，在一个复杂系统中由于多因素的不确定性(如OD，到达规律等)都将影响等车时间的变化，从图4可以看出乘客等车时间与发车间隔和运能基本成正相关关系。

图4 大客流乘客等车时间的趋势化关系

5 结语

本文提出一种城市轨道交通大客流等车时间的计算模型。其特点是利用不同车站乘客实时到达率、列车运能限制和FIFO排队论等约束，将不同车站到达乘客区间化，利用累计输入输出算法，准确计算包括多次延误在内的乘客等车时间。通过模型分析发现缩短发车间隔可减少大客流等车时间延误，此外不同列车运能对乘客等车时间也有正相关影响。模型为非线性规划模型，基于实证案例可以准确计算等车时间、满载率、滞留乘客等客流实时分布的数据，以时间为计算标度，利于探寻列车开行方案的问题，为解决大客流发生时的时刻表优化策略提供了新思路。后续工作将围绕以列车时刻表优化的具体方法和换乘站换乘延误问题作为未来研究方向。

[1] Wardman， M. A review of British evidence on time and service quality valuations[J]. Transportation Research Part E， 2001，37(2-3)：107-128.

[2] 曹志超.网络条件下城市轨道交通突发大客流演化机理和应急策略研究[D].北京：北京交通大学，2013.

[3] Osuna E E， Newell， G.F. Central strategies for an idealized public transport system[J]. Transportation Science，1972，6(1)：52-72.

[4] Welding P I. The instability of a close-interval service[J]. Operational Research Quarterly， 1957，8 (3)：133-142.

[5] Newell， G.F. Dispatching policies for a transportation route[J]. Transportation Science， 1971，5(2)：91-105.

[6] Zhang Q， Han B， Li D. Modeling and simulation of passenger alighting and boarding movement in Beijing metro stations[J]. Transportation Research Part C: Emerging Technologies， 2008，16(5):635-649.

[7] Hurdle V F. Minimum cost schedules for a public transportation route[J]. Transportation Science，1973，7 (2)：109-157.

[8] Daganzo， C.F. Fundamentals of Transportation and Traffic Operations[M]. Pergamon: Elsevier Science Ltd.， 1997:301-302.

[9] Zhou X， Zhong M. Train scheduling for high-speed passenger railroad planning applications[J]. European Journal of Operational Research， 2005，167(3)：752-771.

[10]Zhou X， Zhong M. Single-track train timetabling with guaranteed optimality: branch and bound algorithms with enhanced lower bounds [J]. Transportation Research Part B， 2006，41(3)：320-341.

[11]Liebchen， C. The first optimized railway timetable in practice. Transportation Science， 2008，42(4)：420-435.

[12]李得伟.城市轨道交通枢纽乘客集散模型及微观仿真理论[D].北京：北京交通大学，2007:49-50.

[13]段力伟，文超，彭其渊.突发大客流在城市轨道交通网络中的传播机理[J].铁道运输与经济，2012，34(8):79-84.

[14]Niu H， Zhou X. Optimizing urban rail timetable under time-dependent demand and oversaturated conditions[J]. Transportation Research Part C: Emerging Technologies， 2013(36):212-230.

[15]李得伟，周玮腾.城市轨道交通枢纽客流仿真辅助决策技术与实践研究[J].铁道标准设计，2012(12)：1-4.

[16]邱蓉.地铁平行换乘车站旅客行为及运能分析[J].铁道标准设计，2013(5):8-12.

The Model of Calculating Waiting Time in Urban Rail Transit under Oversaturated Conditions

CAO Zhi-chao， YUAN Zhen-zhou， ZHANG Si-lin， WU Hao-ling

(MOE Key Laboratory for Urban Transportation Complex Systems Theory and Technology，Beijing Jiaotong University， Beijing 100044， China)

When peak-hour demand temporally exceeds the maximum loading capacity of a train during Urban Rail Transit (URT) operation， passengers may not be able to board the next arrival train， and they may be forced to wait in queues for the following trains. As a key element of evaluating transportation service-level and optimizing train schedules， this paper establishes a model to calculate accurately passengers’ waiting times， based on queuing theory and train timetable. In view of passengers’ real-time arriving rates， OD (Original-Destination) distribution， headway and train’s capacity， a cumulative input-output algorithm is developed to solve empirical cases， and the tendency of multi-parameters is analyzed. In order to optimize timetable under oversaturated conditions theoretically， this paper proposes a cumulative approach for waiting time calculation， which can be applied for URT network or bidirectional oversaturated and normal passengers. The effectiveness of the proposed model and algorithm are evaluated with a real-world data set from a bi-directional URT network.

Urban Rail Transit; Oversaturated conditions; Waiting time; Train schedule

2014-06-05；

2014-06-09

国家973项目(2012CB725403)

曹志超(1988—)，男，博士研究生，E-mail:13114215@bjtu.edu.cn。

1004-2954(2015)03-0033-04

U239.5

A

10.13238/j.issn.1004-2954.2015.03.008