一种利用非多边形边缘像素的反走样改进方法
2015-11-23王东晓
王东晓
(同济大学电子与信息工程学院,上海 201804)
一种利用非多边形边缘像素的反走样改进方法
王东晓
(同济大学电子与信息工程学院,上海 201804)
文章指出了一般反走样算法中存在的实质性问题,结合了对于视觉系统的特性分析,总结出对于反走样任务的本质要求,并且提出了一个可以解决此问题的改进方法。该方法除了显著的改善效果,还有计算简单、可适用于任意的采样方式的优点。
反走样;边缘;多边形;颜色值;视觉系统
反走样是计算机图形学和可视化等领域中一个基础而重要的课题。反走样使用的采样方法主要是超级采样(supersampling)和区域采样(area sampling),其中,前者使用了离散的采样点,后者则对整个连续区域进行采样。在超级采样中,除了在一个像素中选取间隔均等的子像素,人们还设计了不同的采样模板。通过对采样模板的不同位置赋予不同权重,例如对接近像素区域中心的位置赋予更大的权重,可以对效果有一定改善,这样的采样模板也称为加权掩膜或过滤器。
在反走样的硬件实现方法中,有 SSAA(supersampling anti-aliasing,超级采样抗锯齿)、MSAA(multisampling anti-aliasing,多级采样抗锯齿)、CSAA(coverage sampling anti-aliasing,覆盖采样抗锯齿)、CFAA(custom filter anti-aliasing,可编程过滤抗锯齿)等。其中,超级采样抗锯齿是其他硬件反走样方法的原型,它采用超级采样,对所有需要绘制的像素进行一样的操作。而多级采样抗锯齿则对位于多边形边缘的像素进行了额外处理,它是GPU实时反走样的主要方法。
硬件工艺水平的提高使得GPU的运算性能日益强大,依赖于此,使用更大的采样倍数变为可能。但原理和事实都已证明,采样倍数的提升对反走样效果的提高很容易达到极限。因此,更好的反走样效果必须诉诸优秀的算法,硬件计算性能的提高只能起到有限的辅助作用。
此外,还出现了一些其他的反走样算法,它们使用了计算复杂的过滤器,或者对采样的结果进行额外的计算,来确定位于多边形边缘的像素的颜色值。本文提出的方法也是基于采样的结果进行计算,然而,本文的提出的方法不仅会重新确定待绘制的像素的颜色值,还会重新确定待绘制像素个数及空间位置。
1 问题及分析
在一般的反走样方法,特别是应用于MSAA的方法中,在经过采样过程后,根据采样结果,将所有需要绘制的像素区分为位于多边形边缘的像素和位于多边形内部的像素两类。进而,对位于多边形边缘的像素,根据其自身和邻域像素上的采样结果,经过一系列的计算确定出其颜色值并绘制。许多算法正是致力于使得这些位于多边形边缘的像素能表现出比采样模板的子像素个数更多的颜色。
这一过程中虽然使得位于多边形边缘的像素之间的颜色过渡变得平缓,但这对于实际的视觉效果来说,并不意味着就一定起到相应的改善作用。一方面,视觉感受的锯齿所产生的原因,并不全在于这些像素之间的颜色对比。另一方面,即便这些算法允许使用比子像素个数更多的颜色,受限于多边形边缘的像素数量,实际上在屏幕上微小的局部范围内能表现出来的颜色数量并没有增加,因此对反走样并没有很大的帮助。
这一问题不仅出现在使用了子像素个数有限的超级采样中,同意也存在于能准确地计算出每个像素和多边形的重叠面积的区域采样中。 图1是用区域采样绘制的一条单通道直线,图 2展示了它放大后的局部。由于采用了区域采样,绘制这条直线所能使用的颜色值的数量已经达到了极限,然而当它以原始大小在常见分辨率的光栅显示器上显示时依然会表现出明显的锯齿状。

图1 用区域采样绘制的直线
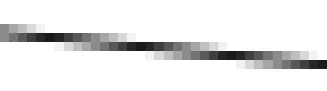
图2 图1放大后的局部
为了探讨一般规律,接下来继续对这个例子进行分析。本例中背景为白色,其归一化的单通道颜色值(以下简称颜色值)为 1,待描绘的理想直线颜色为黑色,即颜色值为 0。由于本例中并未采用特殊的过滤器,混色权重(决定像素颜色值的过程中待绘制理想多边形的颜色值所占的比例)即每个像素中理想多边形覆盖像素的区域面积占像素面积的比例。
如同人体许多感受系统一样,视觉系统对颜色(包括色度和亮度)的敏感程度,和整个视野中感受到的颜色密切相关。一方面,当某颜色接近于视野中整体颜色时,其对视觉系统的刺激较弱,而当某颜色远离视野中整体颜色时,其对视觉系统的刺激较强,会形成强烈的感受。另一方面,当某颜色接近于视野中整体颜色时,人的视觉系统对其分辨能力较高,而当其远离视野中整体颜色时,人的视觉系统对其分辨能力较低。例如,在颜色值为 1的白色背景下,颜色值为0.25的深灰色会比颜色值为0.75的浅灰色给视觉系统带来更大的刺激,形成更强烈的感受。而且,在同样的白色背景下,视觉系统更容易区分颜色值为0.75和0.85的两种浅灰色,而不容易区分颜色值为0.25和0.15的两种深灰色。
对于反走样任务,以上视觉特性会带来的影响是,混色权重较小(即颜色值较接近背景)的像素与背景看起来区分度很大,因而很难形成其颜色值逐渐融入到背景中这一笔者希望的视觉效果。事实上,这些像素更容易和颜色权重较大的像素一起在视觉上组合形成某种固定模式的图案,如图 2中所能观察到的那样。
作为图形学绘制多边形的一个基本做法,笔者会将待绘制多边形的颜色通过权重的方式分配给多边形经过的各个像素。在多数反走样方法中也遵循这一规则。这样可以保证绘制出来的多边形边缘整体上和理想的待绘制多边形看起来颜色相近。如图 2中所能看到的那样,待绘制的理想直线经过一个像素中部的时候,直线上此处的混色权重完全分配给一个像素,而经过两个或多个像素边缘的时候,则是按比例分配给两个或多个像素。
然而,这一规则在反走样任务中实际上是不应该被严格遵守的。因为它既不能保证边缘各处细节看起来颜色均匀,而且由于在各处绘制了不同数量的像素,会导致视觉上形成差异较大的不同图案,这就极其容易放大走样的视觉效果。尤其是当多边形的边缘经过一个像素中部时,必然会形成强烈的走样效果。一方面,由于空间上其他边缘区域使用了多个像素,而此处却只使用了一个像素,形状上差异巨大;另一方面,只使用了一个像素意味着此处的颜色值远远比其他边缘区域更偏离背景颜色值,因此在视觉上更加突出。反走样的根本任务也可以说就是要消除这种边缘上不同区域间的强烈对比。
2 重新确定绘制像素数及其颜色值的改进方法
2.1要求及改进方案
上一节分别从颜色值和空间两个维度上对走样的成因进行了探讨。接下来也将从这两方面提出反走样的改进方案。
首先,混色权重不应该均匀分配。混色权重低而接近背景颜色值的像素,由于其可辨识度实际上很高,这样的相邻像素容易在视觉上共同形成明显的图案。为了使多边形的边缘看起来逐渐融入背景,应该使用更小的混色权重。由于视觉系统对颜色值的区分能力越靠近背景的颜色值越强,本文建议在反走样中使用不均匀的混色权重,即接近 0的混色权重的可用值应多于接近于 1的可用值,这样有利于在视觉上形成平缓的过渡。事实上由于反走样任务的需要,在多边形边缘上使用接近 0的混色权重值的像素数量也应该多于使用接近1的混色权重值的像素数量。
其次,通过采样过程直接确定的混色权重往往会在边缘上周期性地绘制出单个颜色值远离背景的像素,这会和边缘上其他区域形成极其强烈的对比。对此类像素的邻域像素进行重新绘制对反走样效果有极大的帮助。例如,对其 4邻域中混色权重为 0的像素赋予较小的混色权重。同时,为了避免此处区域看起来过于显眼,应降低原单个像素的混色权重。
这样的做法,从空间上看使得多边形的边缘上大部分区域变粗了。这样做是符合常识的,例如宽度分别是3和2与宽度分别是2和1的两组线条之间,前者两条线间的差异看起来显然没有后者大,因此边缘一定程度的加粗对反走样是有利的。事实上,使用更多的像素和使用更多的颜色值一样可以在视觉上造成更加丰富的变化和自然的过渡。在发现从颜色值上进行反走样已经陷入瓶颈的时候,从空间的角度加以考虑和利用便是个自然合理的想法。
2.2方法及步骤
基于以上考虑,本文提出了如下的改进方法。
(1)对原来的根据采样结果确定的混色权重 originalWeight,用如下的函数重新确定:
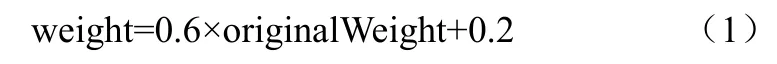
其中originalWeight 不为0,即当采样结果中的子像素数为 0时,不对该像素用此式确定新的颜色值。因此对于范围为(0,1]的混色权重,映射之后范围变为(0.2,0.8],且0.5仍为0.5。
(2)对于每个采样结果为0个子像素的像素(m,n),若其4邻域中的像素存在混色权重大于0.5的像素,则取其中最大的一个混色权重,记为neighbourMaximumWeight(m,n)。将像素 (m,n)上的混色权重决定为

即
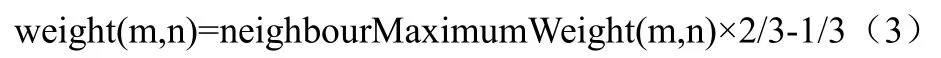
式中的 halfOfSubpixels表示该算法中采样模板的子像素数的一半,但它对结果并未产生影响,因此,这个方法不仅能适用于任何子像素数的超采样,也能适用于区域采样。显然对任意一个在[0.5,0.8]之间的neighbourMaximumWeight(m,n),能确定一个在[0,0.2]之间的weight(m,n)。
(3)同一般决定颜色值的过程,新的颜色值由下面的计算式决定:
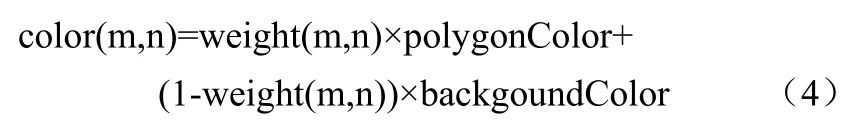
polygonColor和backgroundColor分别是待绘制多边形的理想颜色值和背景的颜色值。
2.3实验结果
对于图1和图2的情况,使用了新方法进行改进后的效果如图3和图4所示。从图1和图3的对比可以看到效果的提升。图 4中可以看到,通过绘制了更多的像素,直线上各处显得粗细均匀。原来狭窄的深色区域现已被浅色像素包围,颜色也有所变浅,因而不再如以前突出。而原来浅色像素共同形成的图案由于向周围延展,且颜色值上过渡细腻,而彼此连成一片。

图3 对图1中的直线用本方法重新绘制

图4 图3放大后的局部
图 5是提供了另一组对比示例,反映出了更多斜率时的情况。其中使用的采样方式是子像素个数为4、采用旋转栅格的超级采样。可以看出,对不同斜率的图形,虽然效果不尽相同,但适用本方法后均有一定程度的改善。
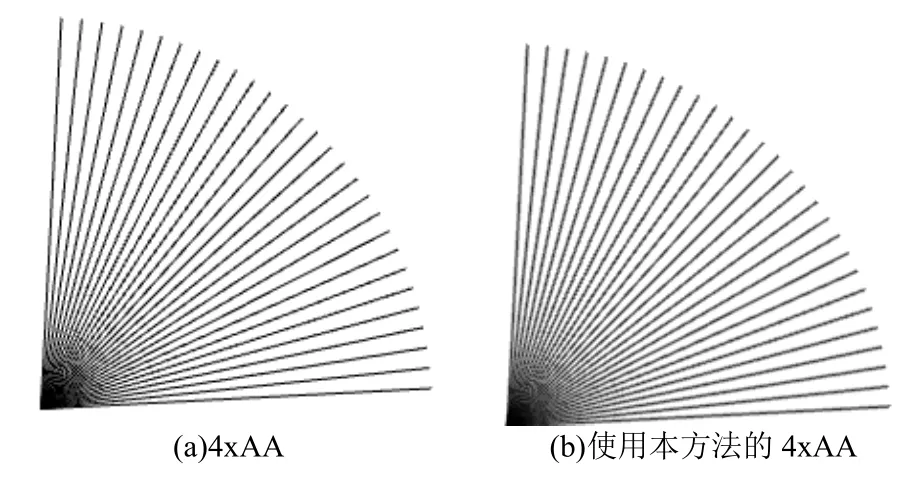
图5 使用本方法前后的4倍反走样效果对比
图6显示了使用本方法前后的局部细节对比。其中(a)和 (b)分别为图5中使用本方法前后的局部效果。(c)和(d)来自另一组对比,其中使用的采样方式是 9个子像素的顺序栅格超级采样。

图6 使用本方法前后的局部效果对比
3 结论
实验证明,本方法能够运用在多数采样方法中,对反走样的效果有明显改善。针对不同的应用目的和场景,可以通过调整式(2)和式(3)中的参数,来调整需要在反走样中绘制的像素数量。例如,如果场景中没有尺寸接近像素大小的物体和图形,则可以在第二步中将查找的阈值降低到0.5以下。也可以在式(1)中调整参数来控制所使用的混色权重在不同范围上的密度。在需要对颜色值进行更加精细的控制时,可使用二次以上的函数替代式(1)、(2)、(3)。
本方法计算简单,效果明显,虽然利用了采样的结果,但不需要依赖于具体的采样方法,对于各种倍数的超级采样和区域采样都适用。它同样也适用于使用了特定采样模板或滤波器的反走样算法,以及根据采样结果计算出更复杂颜色值的算法。在选择绘制像素的思路上它和把子像素延伸到周围像素的采样模板存在一定相似性。在硬件反走样技术上,本方法虽然对采样结果个数为 0的像素也会进行混色的计算和绘制,然而由于这样的像素实际都处在多边形边缘的像素的邻域,因此不仅适用于SSAA,也可以用于MSAA。
[1] Hearn D, Baker M P, Carithers W R. .计算机图形学(第四版)[M].北京:电子工业出版社,2014.
[2] Crow F C.A comparison of antialiasing techniques[J]. IEEE Computer Graphics and Applications,1981,(1): 40-48.
[3] Iourcha K, Yang J C,Pomianowski A.A directionally adaptive edge anti-aliasing filter[C]//Proceedings of the Conference on High Performance Graphics 2009.ACM, 2009:127-133.
[4] Beaudoin P,Poulin P.Compressed multisampling for efficient hardware edge antialiasing[C]//Proceedings of Graphics Interface 2004. Canadian Human-Computer Communications Society,2004:169-176.
[5] Pitteway M L V, Watkinson D J. Bresenham's algorithm with grey scale[J].Communications of the ACM,1980, 23 (11):625-626.
[6] Angel E,Shreiner D.交互式计算机图形学:基于OpenGL着色器的自顶向下方法(第 6版)[M].北京:电子工业出版社,2012.
An improvement solution for anti-aliasing with drawing non-edge pixels
A substantial problem in general anti-aliasing algorithms is pointed out in this paper. With the analysis of human visual system features, it concludes the essential requirements of anti-aliasing task and puts forward a feasible improvement solution. Beside its obvious effect, the solution needs only simple calculation, and could be combined with any type of sampling methods and templates.
Anti-aliasing; edge; polygon; color value; human visual system
TP391.41
A
1008-1151(2015)09-0033-03
2015-08-12
王东晓(1991-),男,同济大学电子与信息工程学院硕士研究生。
