基于分形插值方法的长江口深水航道回淤量计算
2015-11-22窦希萍焦增祥王玉丹
潘 昀,窦希萍,焦增祥,王玉丹,丁 磊
(南京水利科学研究院 港口航道泥沙工程交通行业重点实验室,江苏 南京 210029)
自20 世纪50年代以来,围绕长江口水流泥沙问题开始了大量研究工作,早期主要通过水文泥沙与河床演变分析、水槽和物理模型试验研究长江口泥沙运动机理,80年代末由于数值模拟技术的发展,建立了长江口潮流、波浪、泥沙数学模型,在河口形态[1]、拦门沙[2]、最大浑浊带[3]、泥沙絮凝与沉降[4]、悬沙垂向分布[5]、泥沙扩散[6]、浮泥[7]、航道回淤预测[8]等数学模型方面取得了突破性进展,为长江口深水航道治理工程建设提供了技术支撑。长江口深水航道治理工程采用整治和疏浚相结合,分三期实施,1998年至2005年完成了一、二期工程,包括建设南北槽分流口工程;长分别为48 km 和49 km 的南、北双导堤;总长约30 km的19 座丁坝。主要整治建筑物平面布置见图2。一期工程完成后北槽航道水深达8.5 m,二期工程完成后水深达到10 m,三期工程主要为疏浚,自2006年9月开始疏浚,通过加长丁坝、增加疏浚船只,终于在2010年3月使北槽航道水深达到12.5 m。针对三期工程航道回淤严重的状况,刘猛等[9]研究导堤越堤水沙对航道回淤影响;陈维等[10]研究南沙头通道及横沙通道的影响;沈琪等[11]分洪季特殊月对长江口深水航道的影响以及泥沙来源进行分析;张宏等[12]基于神经网络方法研究深水航道海域悬浮泥沙浓度分布规律。由于北槽深水航道回淤涉及因素众多,现有理论和模拟方法还难于解释和描述这一现象,因此,利用不断积累的北槽航道实测回淤资料,采用合适的方法进行预测分析不失为一条途径。
分形插值是分形几何理论及其应用研究中的一个重要内容,它能很好地刻画现实世界中普遍存在的粗糙的、复杂的、自相似、或自仿射的对象[13]。因此,它在地理地质学、图形与图象处理、计算机动画仿真等许多领域都具有广泛的应用。由于分形插值函数具有很强的灵活性和稳定性[14],只要适当调整其参数,所生产的插值曲线的维数就能取到1 和2 之间的任意值,因此它不仅可用来拟合光滑曲线和平稳数据,更是在不光滑曲线和非平稳数据的拟合中显示出独特的优越性。河流动力学领域,如刘德平[15]运用分形理论和分形维数研究了长江汉口站4 个大洪水年份逐日平均水位、流量过程线的形态特征;马宗伟等[16]分析了长江中下游河流的分析特征,说明了河流形态的分维大小与洪水发生的可能性高低之间的关系;Nikora[17]和钟亮等[18]把分形理论应用到床面粗糙形态的研究。
长江口水域的主要动力因素是径流、潮流和波浪。径流受到三峡枢纽的调控,年内虽有洪枯之分,但是年际间变化不大;外海潮汐呈周期性变化;波浪受季风和台风影响,均具有周期性。由2011年至2013年长江口北槽12.5 m 深水航道月平均实测回淤量(图1)可知,北槽航道沿程的回淤量具有自相似性(相似于图1 中粗黑实线),每月均有数日回淤量达到峰值和每年均有数月回淤量达到峰值。因此,可以采用分形理论进行分析。鉴于现阶段长江口深水航道回淤量预测涉及泥沙来源、动力环境对泥沙回淤的影响机理等暂时无法解决的问题,本文尝试利用分形插值方法对长江口12.5 m 深水航道年回淤变化规律进行探讨,试图揭示综合因素对深水航道年回淤量的影响。
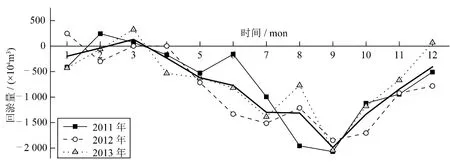
图1 2011年至2013年长江口深水航道月平均回淤量Fig.1 Monthly backsilting quantity in Yangtze Estuary deepwater channel from 2011 to 2013
1 分形插值理论
传统的数学插值拟合函数大都是多项式、有理函数或三角函数等初等函数性组合来表达,而分形插值函数则是用迭代函数系统(IFS)来实现的。经典插值方法是针对欧氏几何描述的对象,而山脉的轮廓、云彩的边缘、粗糙表面的轮廓等图像不能用欧氏函数很好地描述,用分形插值函数就能充分接近这些图像,并且在适当的尺度范围内,它的分形维数趋近于这些数据的分形维数。
分形插值是构造出一个迭代函数系,使目标点集A 为插值函数的一部分。构造目标点集A 等于插值函数f(x)的迭代函数系{R2:Wi,i = 1,2,…,N},方法如下:设迭代函数系中的每个函数Wi是仿射变换,其构造表示为:
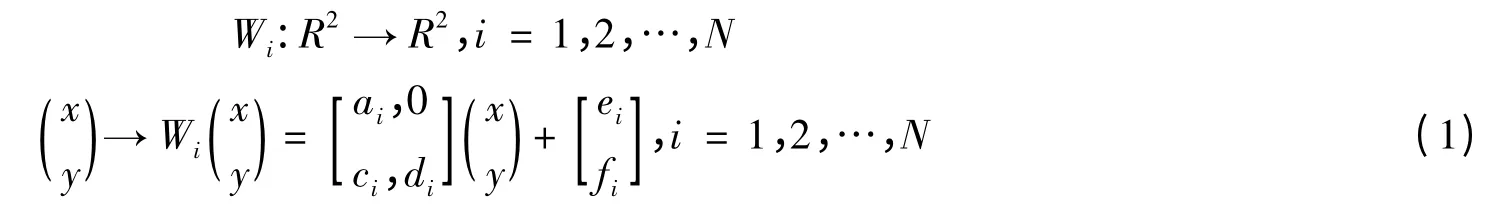
并且满足条件:
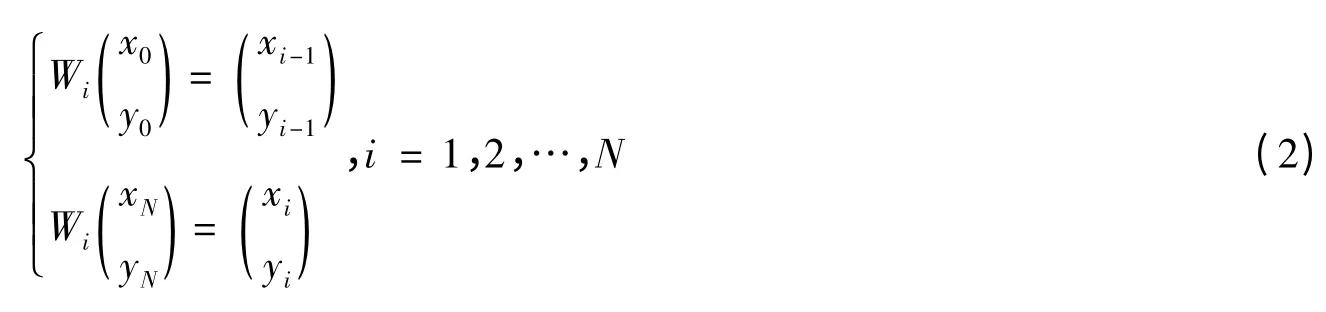
根据式(1)和式(2),对每一个i,仿射变换函数Wi的5 个常数ai、ci、di、ei与fi应该满足4 个线性方程式:
选用早熟、优质、高产,抗病虫、抗逆性强、适应性广、商品性好的品种。当前攀西地区种植较为普遍的品种为豫选一号品种,亩用种量2.5—3.5公斤。菜豆品种有红花青壳、双青玉豆、天马架豆王、泰国架豆王、碧丰8号等。

四个方程有五个变量,所以存在一个自由变量,一般选di为自由变量,并称之为垂直尺度因子。限定这个自由变量满足-1 <di<1(i = 1,2,…,N)。特别,如果取di= 0 ,就可以得到分段线性插值函数。当di是任意限定的实数时,迭代函数系中的每个函数Wi的其他系数利用式(3)可以推导:
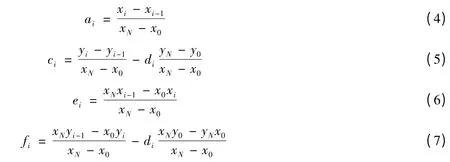
2 时间尺度上回淤量的分形插值曲线
图2 为长江口12.5 m 深水航道疏浚单元分布,2011年至2013年逐月航道回淤量见表1(其中负值表示回淤量,正值表示冲刷量)。采用分形插值方法,取垂直尺度因子-0.5≤di≤0.5(i=1,2,…,N)构造长江口深水航道逐月的回淤量迭代函数系,对其每月回淤量进行分形插值计算。对于航道回淤量而言,垂直尺度因子是一个涉及动力(径流、潮汐和风浪)及泥沙特性(粒径、沉速、粘性)的综合影响因子,取不同的垂直尺度因子,可以得到不同的航道回淤量插值曲线,再对时间进行积分,得到不同的年航道回淤量。所取di绝对值越大,则偏离实测回淤量越大。
根据式(1)~(7),取di为-0.5、-0.4、-0.3、-0.2、-0.1、0、0.1、0.2、0.3、0.4 和0.5 对表1 中12 个月的航道回淤量进行分形曲线插值。由式(1)~(7)可知,第n 次插值后数据点个数为N(N-1)n,并且与实测数据相比,插值后的曲线形成(N-1)n个与实测数据曲线完全相似的分形微元。图3(a)为2011年长江口深水航道月回淤量的折线图和月平均线图。图3(b)、(c)是根据2011年长江口深水航道每月实测回淤量,取不同的垂直尺度因子作三次插值后的曲线。图3(b)曲线有156 个数据点,12 个分形微元;图3(c)有1 872 个数据点,144 个分形微元;图3(d)有22 464 个数据点,1 728 个分形微元。根据分形插值理论,在-1 <di<1 内经过若干次插值后趋近于稳定。由于分形插值方法收敛速度快,所以文中假设第三次插值后曲线基本趋于稳定。同样对2012年和2013年长江口深水航道每月回淤量进行三次分形插值。从三年的实测回淤量来看,7月、8月和9月泥沙回淤量出现峰值,均比其他月份大数倍。因此,当di>0 时随着di的增大,分形微元的峰沿Y 轴负方向增大;当di<0 时随着di的减小分形微元的峰沿Y 轴正方向增大。第三次插值后所得回淤量插值数据点已非常庞大,插值曲线亦非常密集且基本趋于稳定。
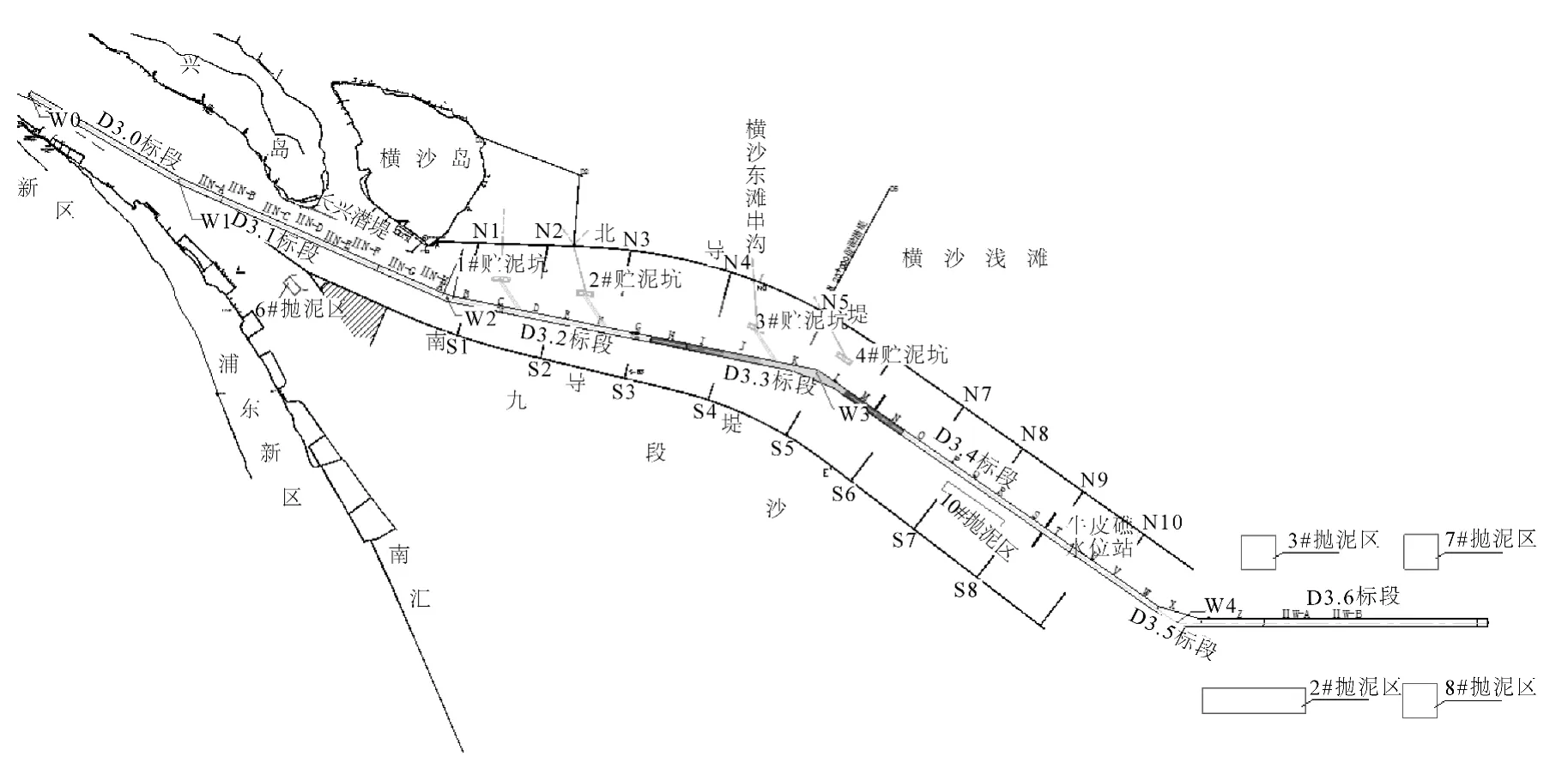
图2 长江口12.5 m 深水航道示意Fig.2 The sketch of Yangtze Estuary 12.5 m deepwater channel
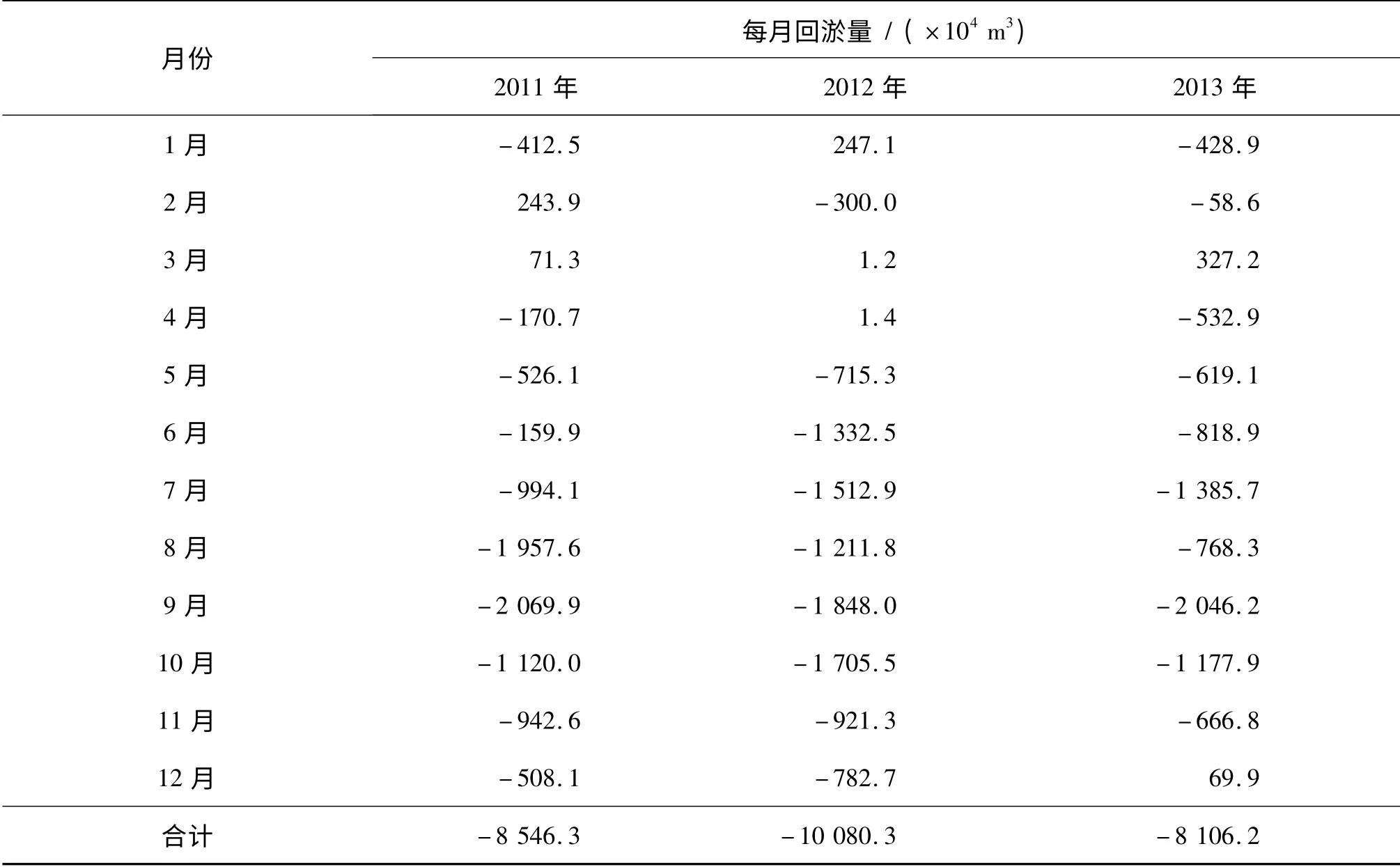
表1 2011年、2012年和2013年长江口深水航道每月回淤量Tab.1 Monthly backsilting quantity in Yangtze Estuary deepwater channel from 2011 to 2013
分形算法在做插值时,采用实测月份的淤积量作为控制节点,相邻月份回淤的插值曲线呈现出控制点的“粗糙的、复杂的自相似”等特征,和实际的月航道淤积的时间序列分布特征并不一致却又相似,即增加了月回淤量之间的分形维数。
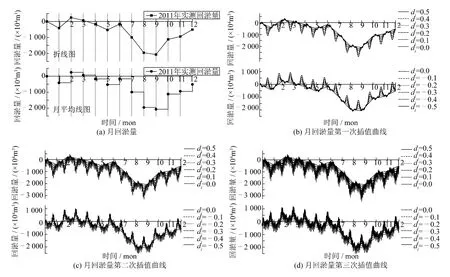
图3 2011年长江口深水航道月回淤量与分形插值曲线Fig.3 Monthly backsilting quantity in Yangtze Estuary deepwater channel and fractal interpolation curve in 2011
3 航道年回淤量计算和分析
3.1年回淤量计算公式构建
插值出的回淤量在时间t 内进行积分即得到年回淤量V:
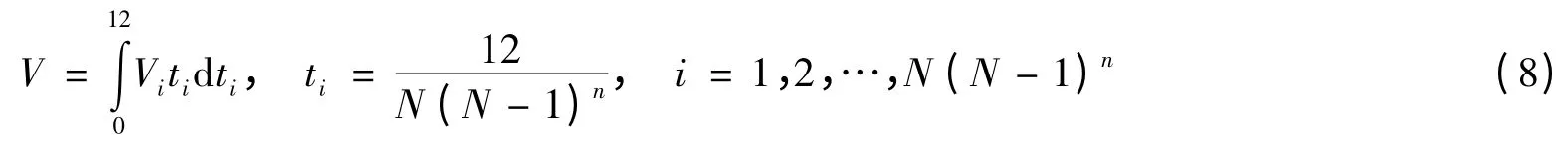
式中:Vi为第i 个月插值出的回淤量,ti为第i 个插值点X 坐标,N 为初始实测数据点个数即为13,n 为分形插值的次数n=1,2,3。
式(8)计算的年回淤量即图3(a)折线图中折线与X 轴围成的面积,而所有月回淤量的和即图3(a)月平均线段与X 围成的面积,两种方法计算年回淤量略有差异。图4 为2011年、2012年和2013年长江口深水航道年回淤量与di的变化关系图,并对曲线进行公式拟合。
2012年和2011年回淤量曲线相似,作一次插值所得到的直线的斜率相差较小,最小年回淤量为5 670 ×104m3,最大年回淤量为14 057 ×104m3。2013年作一次插值所得到的直线的斜率相差较大,长江口深水航道年回淤量最小值为3 860 ×104m3。
图4 中实心点及曲线为作三次分形插值计算得出的年回淤量,空心点是所拟合公式的计算值,R 为相关系数(R1= R2= R3= 1 )。从图4 中可知,不同垂直尺度因子di作一次插值得到的年回淤量为直线,作二次插值得到的年回淤量为二次曲线,作三次插值得到的年回淤量为三次曲线,且高次项的系数均等于作一次插值所得到的直线的斜率。
分形插值得到的年回淤量三次曲线和二次曲线均与作一次插值所得到的直线相切,且切点为垂直尺度因子为0 时实测回淤量根据式(8)计算得到的年回淤量,即Y 轴的截距。综上所述,可以得出长江口12.5 m 深水航道年回淤量的计算公式:
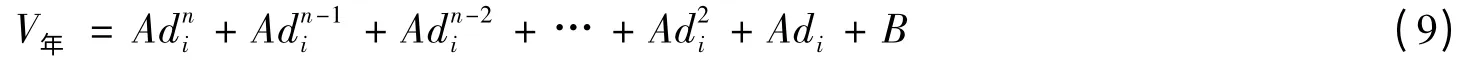
式中:A 为作一次插值所得到的直线的斜率,B 为12 个月实测根据式(8)计算得到的年回淤量,n 为分形插值的次数n=1,2,3。式(9)中的系数A 与每年长江口深水航道月回淤量的曲线形状有关系,实数B 是某年长江口深水航道的实测年回淤量。
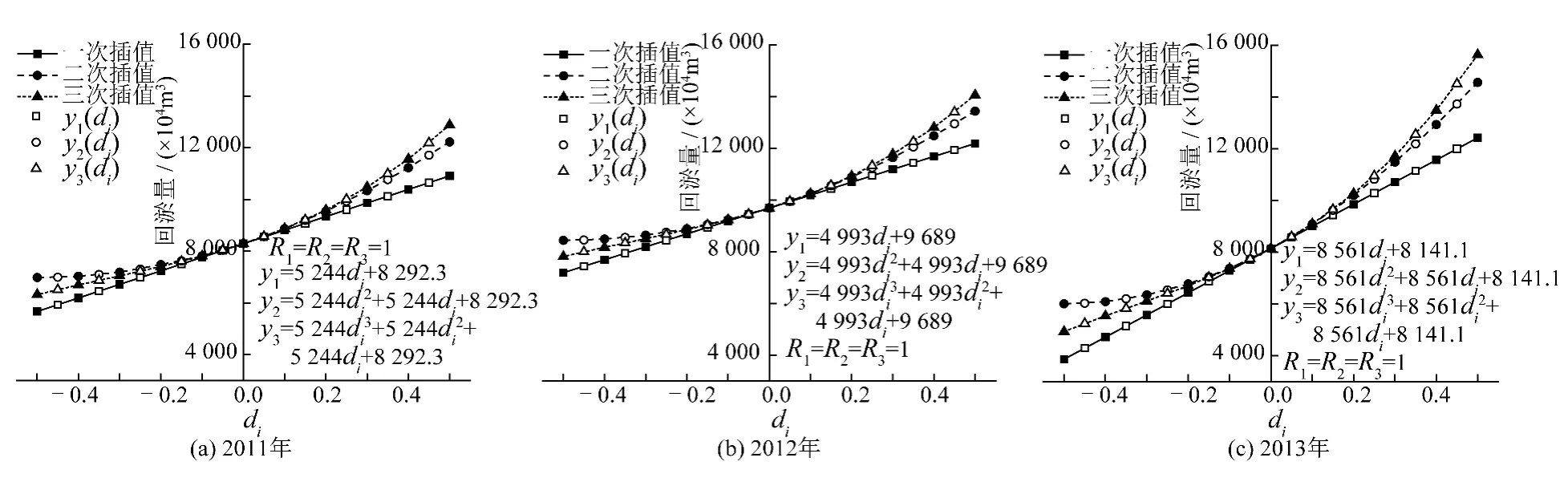
图4 长江口年回淤量及拟合公式Fig.4 Annual backsilting quantity in Yangtze Estuary channel and fitting formula
3.2 垂直尺度因子对航道年回淤量的影响
由于式(9)中系数A 和B 不确定因素较多,且直接受某年长江口深水航道实测回淤量的影响,所以对式(9)进行如下处理:
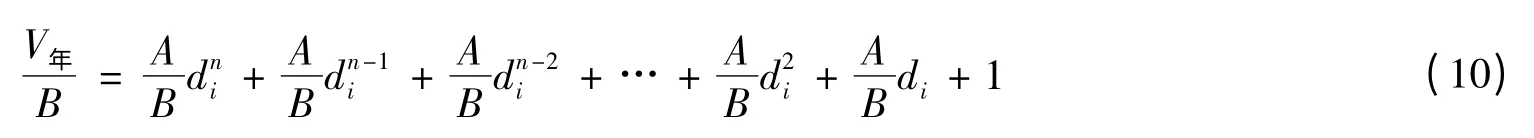
式(10)中可以定义V年/B 为某年长江口深水航道相对回淤量。
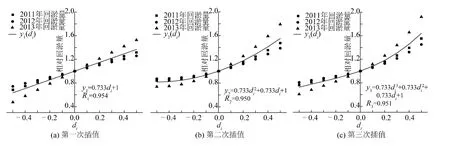
图5 相对年回淤量公式拟合Fig.5 The fitting formula of the relative annual backsilting quantity
图5 为2011年、2012年和2013年相对回淤量各次插值数据拟合曲线。拟合曲线的相关系数均在0.95左右,于是可以得出长江口12.5 m 深水航道年相对回淤量计算公式:
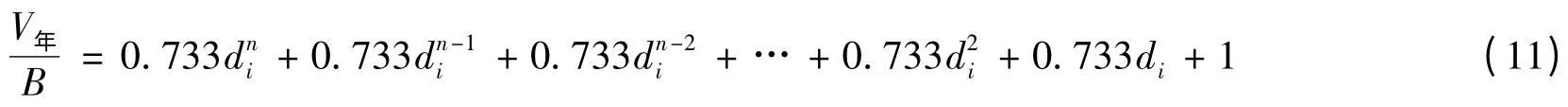
式(11)中如果系数B 取多年平均值,则依据垂直尺度因子di可对长江口深水航道年回淤量进行预测和评估。若n 取无穷大,且-1 <di<1 式(11)可简化为:

取B 为2011年、2012年和2013年深水航道年回淤量的平均值8 707.5 ×104m3。根据2011年、2012年和2013年深水航道年回淤量(V年)和式(12),反求di依次为-0.026、0.177 和-0.104。考虑年际间的影响,按照三年平均回淤量与最大和最小回淤量之比20%调整di的范围为-0.12≤di≤0.20,则近些年长江口深水航道年回淤量的变化范围:8 023.7 ×104m3≤V年≤10 303.2 ×104m3。当取di= -0.5 时,其年最小回淤量为6 580 ×104m3;当di= -1 时,得到年极限最小回淤量为5 516 ×104m3。
4 结 语
依据2011 至2013年长江口12.5 m 深水航道实测年回淤量资料,采用分形插值方法,取垂直尺度因子-0.5≤di≤0.5(i=1,2,…,N)对长江口深水航道回淤量预测进行了初步研究。主要结论如下:
1)分形插值可以较好地反映长江口12.5 m 深水航道的月回淤量的变化态势并通过调整垂直尺度因子,可以得到包含动力和泥沙特性在内的综合因素对深水航道年回淤量的影响。
2)根据2011 至2013年12.5 m 深水航道年回淤量资料,确定了垂直尺度因子的变化范围为-0.12≤di≤0.20。由此计算得到近些年的年回淤量的变化范围为8 023.7 ×104m3≤V年≤10 303.2 ×104m3,其最小回淤量为6 580 ×104m3以及年极限最小回淤量为5 516 ×104m3。
3)由于目前长江口12.5 m 深水航道只有3年的回淤资料,因此该方法的有效性尚待更长时间资料的检验。
[1]CHEN J Y,YU C X,XU H G.The model of the Changjiang Estuary during the last 2000 years,Estuarine comparison[M].Massachusetts:Academic Press,1982:655-666.
[2]潘定安,孙介民.长江口拦门沙地区的泥沙运动规律[J].海洋与湖沼,1996,27(2):279-286.(PAN Dingan,SUN Jiemin.The sediment dynamics in the Changjiang River Estuary mouth bar area[J].Oceanologia et Limnologia Sinica,1996,27(2):279-286.(in Chinese))
[3]李九发,时伟荣,沈焕庭.长江河口最大浑浊带的泥沙特性和输移规律[J].地理研究,1994,13(1):51-60.(LI Jiufa,SHI Weirong,SHEN Huanting.Sediment properties and transportation in the turbidity maximum in Changjiang Estuary[J].Geographical Research,1994,13(1):51-60.(in Chinese))
[4]张志忠,阮文杰,蒋国俊.长江口动水絮凝沉降与拦门沙淤积的关系[J].海洋与湖沼,1995,26(6):662-669.(ZHANG Zhizhong,RUAN Wenjie,JIANG Guojun.The relationship between flocculating settlement in flowing water and deposition in the Changjiang River[J].Oceanology et Limnology Sinica,1995,26(6):662-669.(in Chinese))
[5]时钟,凌鸿烈.长江口细颗粒悬沙浓度垂向分布[J].泥沙研究,1999(2):59-64.(SHI Zhong,LING Honglie.Vertical profiles of fine suspension concentration in the Changjiang Esturary[J].Journal of Sediment Research,1999(2):59-64.(in Chinese))
[6]盛升国,施厚庆,于福生,等.长江口北槽航道抛泥区泥沙扩散的试验研究[J].泥沙研究,1986(3):37-47.(SHENG Shengguo,SHI Houqing,YU Fusheng,et al.Sedimentation committee of chinese society of hydraulic engineering accepts the consulting of sedimentation problems[J].Journal of Sediment Research,1986(3):37-47.(in Chinese))
[7]徐建益,袁建忠.长江口深水航道建设中的浮泥研究及述评[J].泥沙研究,2001(3):74-82.(XU Jianyi,YUAN Jianzhong.Study on the fluid mud in the Yangtze Estuary[J].Journal of Sediment Research,2001(3):74-82.(in Chinese))
[8]DOU X P,LI T L,DOU G R.Numerical model of total sediment transport in the Yangtze estuary [J].China Ocean Engineering,1999,13(3):277-286.
[9]刘猛,吴华林,李为华,等.长江口深水航道工程南导堤越堤水沙运动观测研究[J].海洋工程,2013,31(3):129-140.(LIU Meng,WU Hualin,LI Weihua,et al.Observational study on flow and sediment transport overtopping the south leading jetty in the Yangtze Estuary Deepwater Channel Regulation Project[J].The Ocean Engineering,2013,31(3):129-140.(in Chinese))
[10]陈维,匡翠萍,顾杰,等.南沙头通道及横沙通道对长江口深水航道的影响分析[J].海洋科学,2013,37(4):75-81.(CHEN Wei,KUANG Cuiping,GU Jie,et al.Influences of the Nanshatou Passage and Hengsha Passage on sediment deposition in Deepwater Navigation Channel of the Changjiang River Estuary[J].Marine Science,2013,37(4):75-81.(in Chinese))
[11]沈淇,顾峰峰,万远扬,等.长江口洪季北槽深水航道区域悬沙沉降速度估算[J].海洋工程,2013,31(2):88-94.(SHEN Qi,GU Fengfeng,WAN Yuanyang,et al.Settling velocity of suspended sediment at the North Passage Deep-water Channel of the Yangtze Estuary in the flood season[J].The Ocean Engineering,2013,31(2):88-94.(in Chinese))
[12]张宏,韩震.基于神经网络的长江口深水航道海域悬浮泥沙浓度研究[J].海洋通报,2010,29(2):213-219.(ZHANG Hong,HAN Zhen.Research on suspended sediment concentration of the Yangtze River Estuary Deepwater Channel sea ares using neural network[J].Marine Science Bulletin,2010,29(2):213-219.(in Chinese))
[13]BARNSLEY M F.Fractal functions and interpolation[J].Constr.Approx.,1986,2:303-329.
[14]WANG H Y,YU J S.Fractal interpolation functions with variable parameters and their analytical properties[J].J.Approx.Theory,2013,175:1-18.
[15]刘德平.分形理论在水文过程形态特征分析中的应用[J].水利学报,1998(2):20-25.(LIU Deping.The application of fractal theory in hydrologic process shape characteristic analysis[J].Journal of Hydraulic Engineering,1998(2):20-25.(in Chinese))
[16]马宗伟,许有鹏,李嘉峻.河流形态的分维与洪水关系的探讨[J].水科学进展,2005,16(4):530-534.(MA Zongwei,XU Youpeng,LI Jiajun.River fractal dimension and the relationship between river fractal dimension and river flood[J].Advance in Water Science,2005,16(4):530-534.(in Chinese))
[17]NIKORA V I.Fractal structures of river plan forms[J].Water Resources Research,1991,27(6):1327-1333.
[18]钟亮,许光祥.床面粗糙形态的二元分形插值模型[J].水科学进展,2011,22(5):662-668.(ZHONG Liang,XU Guangxiang.Bivariate fractal interpolation for estimating rough channel bedform[J].Advance in Water Science,2011,22(5):662-668.(in Chinese))
