适用于曲边界的浅水非线性波浪数值模型

张俊生，滕 斌

(大连理工大学 海岸和近海工程国家重点实验室，辽宁 大连 116024)

近岸及港口工程以及远海浅滩上的人工岛修建都必须考虑浅水波浪的作用和影响，而浅水非线性波浪数值模型则是其重要分析和计算工具。要做到计算准确、结果有效，必须满足三个基本方面要求:1)能真实有效地模拟浅水非线性波浪;2)能在水深变化的大范围水域内计算;3)能对曲边界准确求解。这是浅水波浪特性、相关工程海域海底与边界的现实需求。

Boussinesq 方程(以下简称为“B 方程”)是典型的浅水波浪数学模型，能够准确描述浅水波浪的特性。Peregrine［1］推导出了适用于变水深三维问题的二维简化B 方程。其二维简化和变水深的特点使得B 方程成为分析浅水波浪的高效工具，能够实现大面积水域内的波浪模拟。其后诸多学者不断在色散性、非线性方面改进。Nwogu［2］和Beji 等［3］分别推导出了具有较高色散关系的二阶方程。前者能保证方程线性化后计算的波浪相速度在O(μ4)的精度时仍与Airy 波相速度相匹配，后者的线性化色散关系能达到线性波浪理论色散关系的二阶Padé 逼近，且方程形式简单，利于有限元法的数值计算。Gobbi 等［4］和Madsen 等［5］诸多学者则提出了具有更高色散性、更强非线性的高阶方程。

在数值方法上，有限差分法因求解简单、程序实现方便被大量使用，Gobbi 和Madsen 便使用了有限差分法进行求解。但是，有限差分法对曲边界的处理是非常困难的，而实际工程中曲边界却大量存在，因此对边界有更好适应性的有限单元法得到了探讨和应用。Li 等［6］、Walkley［7］和Zhao 等［8］采用了有限元方法求解方程。在采用等参单元的情况下，有限元法无法求解四阶及以上导数，三阶导数也只能利用中间变量降阶为二阶，然后利用格林公式转化为空间导数只有一阶的边界积分求解，以上学者均如此处理。而若不采用等参单元，求解将非常困难。因此高阶方程对有限元方法是不能适用的。但对于浅水问题而言，含有三阶空间导数的Beji 改进型方程足以适用，且其形式简单，便于有限元方法应用。

有限元法的优势是对曲边界的处理，但遗憾的是上述学者的计算却并不理想。Li 等［6］、Zhao 等［8］和孙忠滨等［9］均基于Beji 改进型方程的有限元模型给出了圆柱面上浅水波浪爬高的计算结果，但与Isaacson［10］的试验和解析计算结果相比，差别较大。有限元方法的优势没有得到体现。

文中建立的有限元模型利用类似于Engelman 等［11］提出的方法，在边界上对方程进行了从x、y 方向到法线、切线方向的矢量分量变换，准确地利用了边界条件求解。同时，利用Fenton［12］提出的非线性规则波浪解建立了准确的造波方法，从而构建了一个能够准确求解的、适用于曲边界的浅水非线性波浪模型。

1 数值模型的建立

1.1 控制方程

Beji 提出的改进型B 方程的形式:

其中，u = (u，v)为水深平均的水平速度矢量，η 为波面高度，d(x，y)为水深，g 为重力加速度，下标t 为时间导数，▽= (∂/∂x，∂/∂y)为二维梯度算子。Li 等［6］已验证β = 1/5 时，方程的色散性最佳。

为求解式(2)中的三阶空间导数，引入变量a = ∂η/∂x 和b = ∂η/∂y，得:

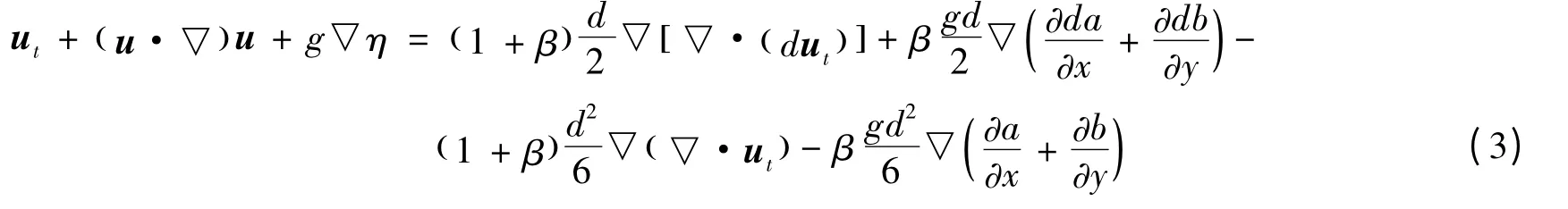
a 和b 的求解采用Li 等［6］的面积加权平均值方法，即

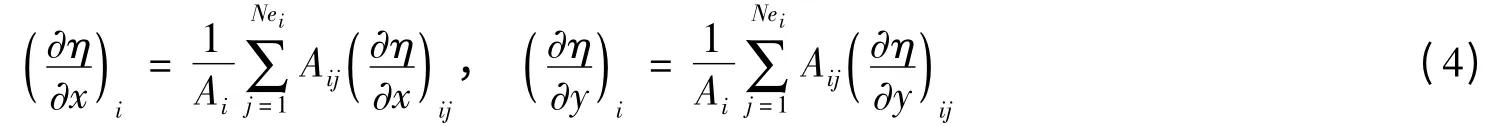
其中，Nei是围绕i 节点的单元总数，Aij是围绕i 节点所有单元中的第j 个单元的面积，(*)ij表示的是在第j个单元中求出的i 节点相关值，Ai是围绕i 节点所有单元的面积和，(*)i为面积加权平均后求出的i 节点的值。1.3.2 节中将给出a 和b 在边界上的求解方法。

1.2 空间离散

利用伽辽金法，对式(1)、(3)离散。在处理式(3)时，利用格林公式将含二阶导数的面积积分转化为只含一阶导数的边界积分。这样，可用等参单元求解，在单元内任意点上有:

其中，f 为任意变量，fj为该变量在单元各节点上的值，Nj为形函数，K 为单元节点数。得离散方程:

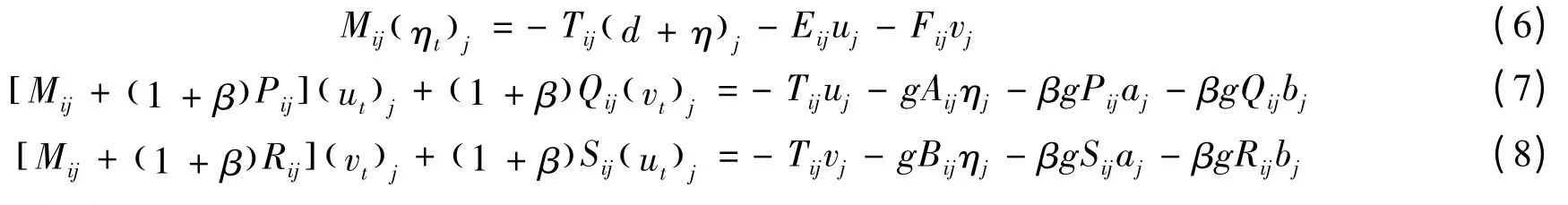
各系数矩阵具体表达式:

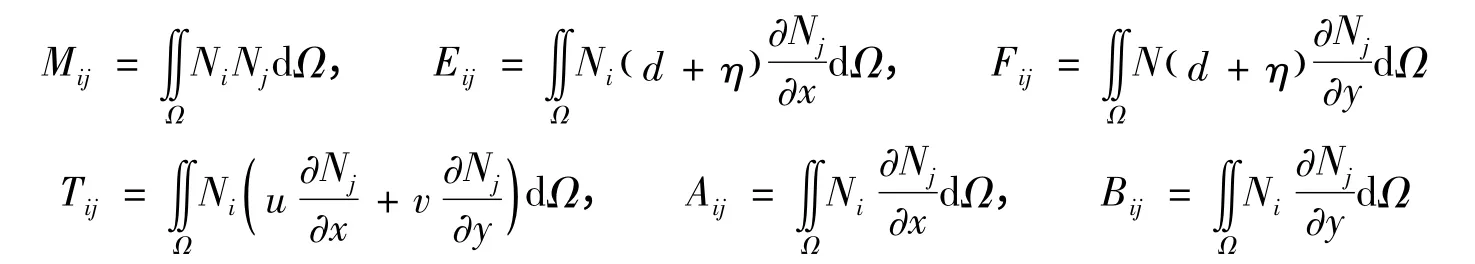
为方便起见，若以x1、x2代替x、y，则Pij、Qij、Rij、Sij可统一表示为

其中，Pij:δ = 1，l = 1;Qij:δ = 1，l = 2;Rij:δ = 2，l = 2;Sij:δ = 2，l = 1。

1.3 边界条件

1.3.1 入射边界

文中采用Fenton［12］提出的非线性规则波浪解作为入射边界条件，其具体表达式:

其中，Ψ = jk(xcosφ + ysinφ － ct)，k 为波数，c 为波速，φ 为波浪入射方向与x 方向夹角，U 为计算所得流速，Bj、Yj为两组傅里叶展开系数，N 为展开多项式项数，文中取为20。k、c、U、Bj、Yj均可根据已知波浪参数由一套方程组求得，Fenton 给出了该方程组求解的方法。

1.3.2 全反射边界

全反射边界条件:

和

其中，n(nx，ny)为边界外法向单位向量。该条件在计算中如何在曲边界上得到满足是计算准确性的关键。Li 等［6］在曲边界上对所有的速度均取为零;Zhao 等［8］则在边界上以式(11)直接替换动量方程;孙忠滨等［9］则根据边界上法向矢量分量nx、ny大小的不同，以式(11)代替不同方向的动量方程，此法仅为避免nx、ny中趋于0 的量在求解方程组时做分母，本质上还是在曲边界处直接求解x、y 方向的速度分量u、v，曲边界处求解的准确性并没有提高。

这里采用速度矢量分量变换的方法处理边界上的计算。设直墙边界处单位切向量为τ(τx，τy)，且满足τ = k × n，对所求速度进行分量转换，有:

其逆变换可写为:

将式(14)代入式(7)、(8)，在方程组中直接求解直墙边界上的un、uτ。对于这些边界节点处的动量方程需做转化，以式(11)直接代替x 方向动量方程，以切线方向动量方程代替y 方向动量方程。切线方向动量方程为:

其中，Mx、My为x、y 方向动量方程。

求解a = ∂η/∂x 和b = ∂η/∂y 时，在直墙边界处同样以求解∂η/∂n 和∂η/∂τ 替代之。如此，全反射边界条件式(12)可直接应用，同时利用面积加权平均值求解∂η/∂τ:

当地优势资源容易得到充分挖掘。农村当地优势资源主要是基础性生产要素，如独具特色的地质地貌、历史人物、宗教圣地、传统工艺及民俗风情等自然资源与文人资源，农民工返乡创业集群通过有形和无形的合约推动技术进步、金融互助、生产销售和服务联合等，实现优势资源的有效整合，打造集群的竞争优势，从而以点带面带动整个区域产业集群全面发展。

最后，在全反射边界上的i 节点处可得:

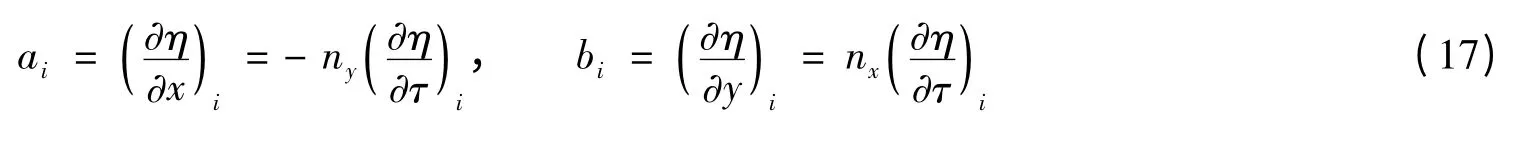
1.3.3 吸收边界

为避免波浪在开边界处反射，在计算域的开边界前布置一阻尼层吸收波浪。文中给出阻尼层为:

1.3.4 松弛区的使用

为了避免反射波浪对入射边界的影响，采用Wang ＆Liu［13］类似的“松弛区方法”，如图1 所示。此种情况下，入射边界扩展为造波区，1.3.1 节中的入射条件解析式在整个造波区内给出。每时刻，松弛区内造波解析解与数值计算结果按照一定权重相加，以耗散掉反射到造波区的波浪，具体表达式:

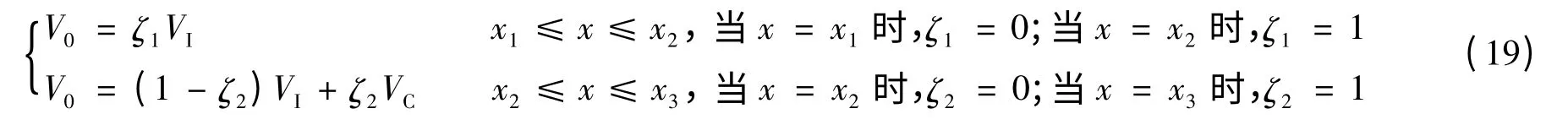
其中，V 表示所计算的变量，下角标0 表示计算的有效结果，下角标I 表示造波解析解，下角标C 表示数值计算结果，ζ 为加权系数函数，本文采用式(18)。该方法可由后续算例证明行之有效。

图1 松弛区布置示意Fig.1 Position of the relaxation zone

1.4 时间积分

采用四阶Adams－Bashforth－Moulton 预报－校正方法进行时间积分计算。但为保证准确，前4 个时间步采用单步的四阶Runge－Kutta 法进行计算。

若把时间积分方程表达为

其中，上角标(n)表示t = nΔt 时刻各变量所取或求得的值。预报出预估值后，进一步用四阶的Adams－Moulton方法进行校正，具体表达式为

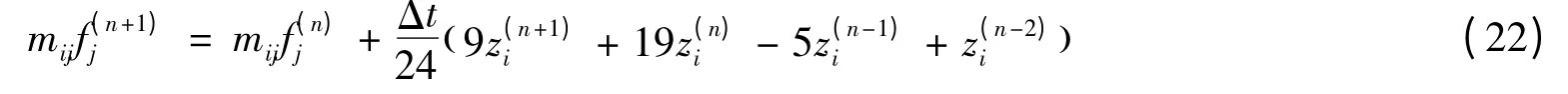
以所有计算节点的相邻两次校正结果的相对误差的加权平均值作为结果收敛的判别标准，表达式:

其中，上角标(n+1)表示当前一次校正结果，上角标(n+1)'表示上一次校正结果。文中取Δf = 10－5为时间积分收敛的判别标准。

求解速度变量的传统做法［6，8－9］为在方程(7)、(8)中分别求解u、v，求解其中的一个变量时，另一个则作为已知处理。于是，两套方程组求得的u、v 需彼此反复迭代，直至结果收敛。这种解法效率不高，且易发散。在解方程时把方程(7)、(8)视做一个方程组同时求解u、v，利用1.3.2 节中对边界的处理方法，直接求解边界处法向速度和切向速度。方程组数值解法上，采用“重开始广义极小残量法”(GMRES(k)，k 为计算中重开始迭代步数，文中取k=100)，该方法效率高，计算准，收敛快。Brussino ＆ Sonnad［14］给出了GMRES 及其它一些线性方程组数值解法的运算过程和效率比较。u、v 的收敛则分别以满足式(23)来判别。

计算时间积分时，CFL 条件需要满足:

其中，c 为波速，Δlmin为最小单元尺度。

浅水非线性波浪波峰窄而尖、波谷平而宽，必须有足够的网格才能捕捉到有效的波形，否则计算失去准确性。Ursell［15］的研究已明确指出参数Ur= H/(k2d3)是描述浅水波浪波形的唯一参数，是衡量非线性的标准，被称为“Ursell 数”。为方便使用，从Ur= 0.05 到16.20，每隔0.05 取一个波形，共324 个，通过对Fenton解析解和本文数值结果进行分析，拟合出浅水规则波一个波长所需划分单元数的经验公式:

后续算例验证了该式的准确性。

2 数值模型的验证

2.1 造波的验证

为验证本文模型模拟非线性波浪的效果，现计算两组、八个波形，并与Fenton 方法［12］的解析解进行对比。计算域为12 m×2 m，水深d = 0.08 m，在计算域的右侧铺设一个入射波长宽度的阻尼层，吸收波浪。具体波浪参数如表1 所示。

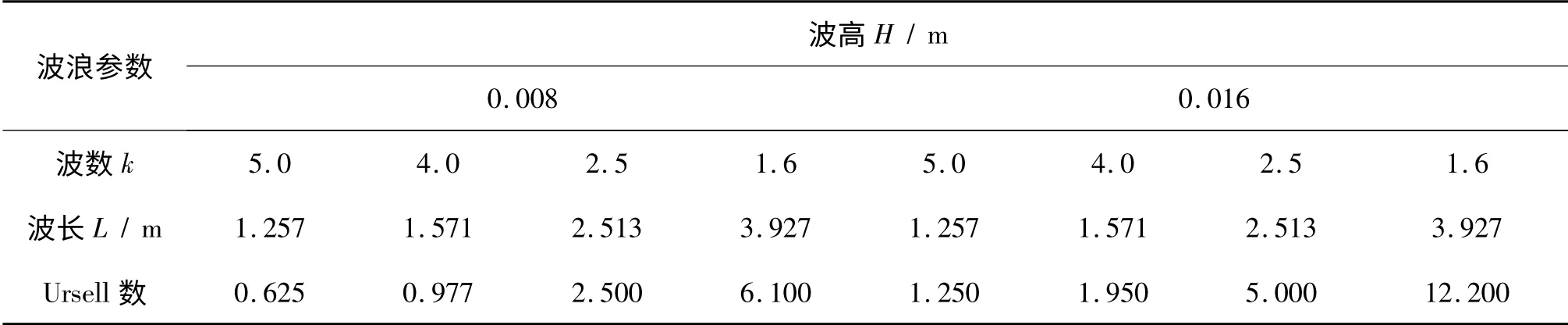
表1 造波测试的波浪参数Tab.1 Parameters for the test of wave generation

两组算例的波高不同，波长对应、依次增加，形成了非线性不同的8 个规则波浪，与解析解的比较结果如图2 所示，该图给出的本文结果均为时间达到20 个入射波周期时(t = 20T)的计算波面。

由图2 可以明显地看到，不论非线性的大小，本模型的结果与解析解都十分吻合，且计算稳定，20 个周期后，算出的波面仍然光滑、准确。其中，图2(h)的Ursell 数最大，此时波浪非线性已非常强，由图2(h)可以看出波谷非常宽且平，贴近静水面，但计算仍能准确地模拟出该波浪。由此可见，本模型的造波方法行之有效，数值计算准确，求解结果稳定。同时，亦可看到采用的阻尼层有显著的消波效果。

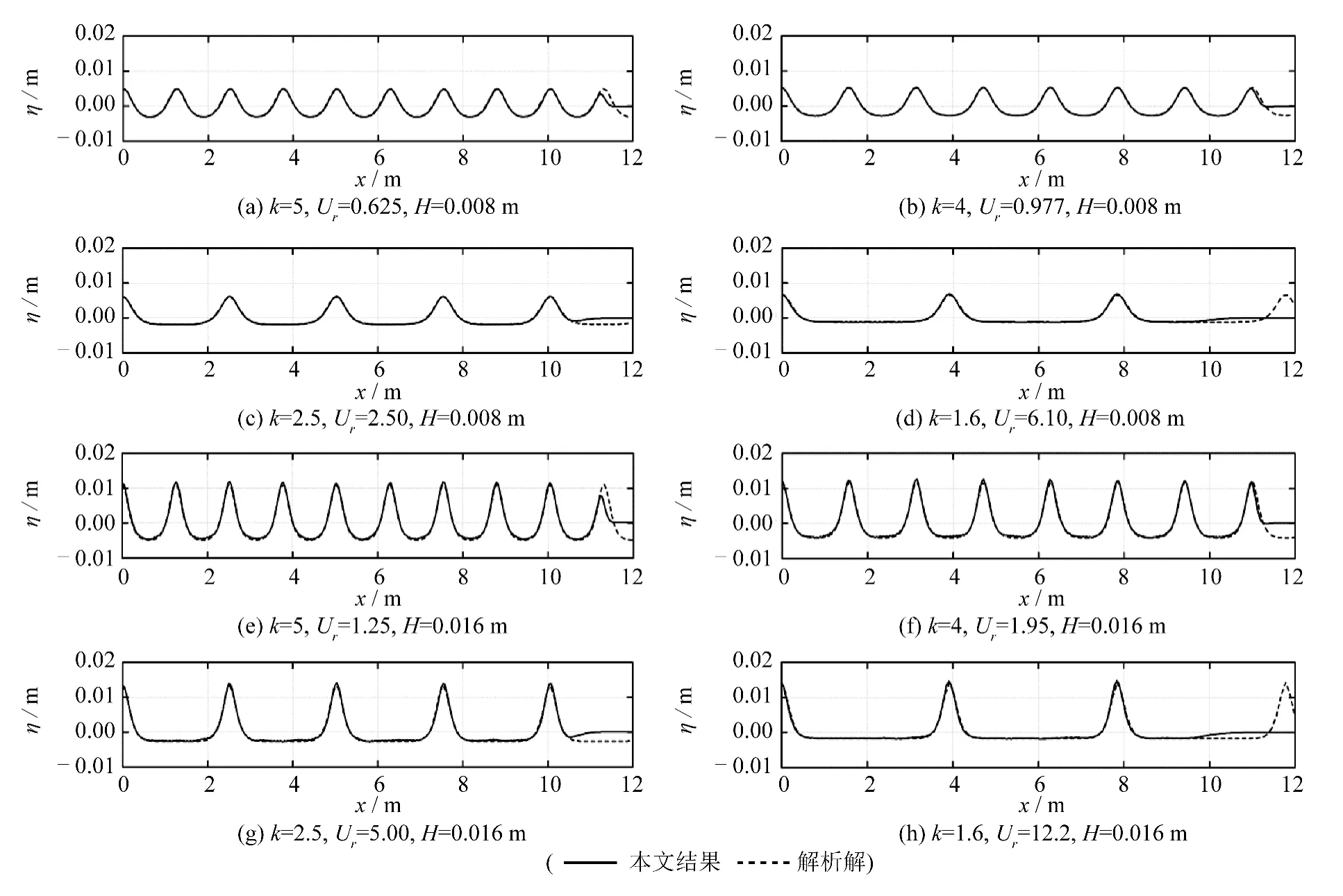
图2 非线性规则波计算结果与解析解比较Fig.2 Comparison between the present result and the analytical result for nonlinear waves

图3 椭圆形浅滩上波浪传播计算域Fig.3 Computational domain over the elliptical shoal

2.2 波浪在变化地形上传播的验证

为验证本文模型适用于计算大面积水深变化水域的波浪模拟，对Berkhoff 等［16］的椭圆型浅滩上波浪传播的试验进行数值计算。计算域为长24.5 m、宽20 m 的矩形区域，模拟的海底地形为斜坡上隆起椭圆半球，地形具体表达式为:

1)不考虑椭圆半球，斜坡上的水深为

其中，x' = xcos20° － ysin20°，y' = xsin20° + ycos20° 。

详细计算域如图3 所示，图中标出了x－y 与x' －y'坐标系、地形等高线以及造波区、松弛区和阻尼层的布置位置。入射波浪为波高HI= 0.046 4 m、周期T = 1 s 的规则波。

采取Walkley［7］的做法:共计算波浪传播50 个周期，取第44、45 周期的结果进行分析，得每一点的波高H，求出相对波高H/HI。共取出x=1、3、5、7、9 m 和y = －2、0、2 m 八个断面的结果与Berkhoff 等的试验结果及Walkley 的数值计算结果进行比较，如图4 所示。本文结果与另二者吻合较好，说明本文模型能准确地模拟出大面积区域地形变化对波浪传播的影响，计算稳定，显现出了波浪的折射、绕射效果。图5 给出了t=45 s(45 个周期)时，波浪传播的透视图，图中同时显示了地形，可以很明显地观察出地形对波面的影响。

图4 椭圆形浅滩上波浪传播计算结果比较Fig.4 Comparison of wave heights in various sections

2.3 曲边界计算的验证

为验证本文模型对曲边界计算的准确性，现对波浪在圆柱上的爬高进行计算。Isaacson［10］给出了四组浅水波浪爬高试验，是由两个不同大小的圆柱和两个不同非线性(Ursell 数不同)的波浪进行的不同组合，Isaacson 同时也给出了其演算的解析解。对于数值方法而言，此问题的计算就是对曲边界计算能力的考验。正如引言所说，绝大多数B 方程的数值模型采用了有限差分法，因而丧失了对曲边界准确计算的能力，故回避了该问题。在为数不多的有限元方法中，Li 等［6］、Zhao 等［8］和孙忠滨等［9］进行了圆柱上波浪爬高的计算，但只对照Isaacson 试验中的第四组给出了结果，且计算结果并不理想。

文中对Isaacson 的四组试验都进行了计算，表2 给出四组试验的参数。

图5 椭圆形浅滩上波浪传播透视图Fig.5 Perspective of the wave elevation over the elliptical shoal

表2 圆柱面波浪爬高试验参数Tab.2 Parameters for the test of wave run-up on a cylinder

因测试波浪为平行于x 方向入射，故为了提高计算效率，利用对称性，只取半个计算域简化计算。如图6 所示，半个圆柱放置于一侧边墙处，计算域长10.5 m，宽4.0 m，造波区、松弛区和阻尼层分别置于计算域的两侧，且宽度皆为入射波的波长，θ 作为描述圆周的参数。

在分析计算圆柱面波浪爬高时，必须排除圆柱绕射波浪在图6 所示的上侧边墙反射后形成的反射波对波浪爬高结果的影响。考虑到两个测试波浪的波长(1.570 8 m 和1.208 3 m)，该计算域4 m 的宽度可以保证至少4 个周期的爬高结果是不受干扰的，因此，文中取前4 个周期的计算结果进行分析。在网格划分方面，圆柱周围需要加密，半圆周分为80 个单元，如图7 所示。

图6 圆柱面波浪爬高计算域Fig.6 Computational domain in the test of wave run up on a cylinder

图7 圆柱周围网格划分示意Fig.7 Mesh around the cyliner

图8 圆柱面上波浪爬高计算结果比较Fig.8 Comparison of results of wave run－up on a cylinder

图9 波浪在圆柱周围绕射透视图Fig.9 Perspective of the wave diffraction around a cylinder

图8 给出了本文计算结果、Isaacson 试验和解析计算结果以及线性理论结果，可以很明显地看出在四组试验中本文结果与Isaacson 的计算结果都吻合地很好，且在第Ⅰ、Ⅱ、Ⅳ组试验中二者与Isaacson 的试验结果也很接近，只第Ⅲ组相差较大。但值得注意的是，第Ⅲ组的测试波浪与第Ⅳ组相同，但圆柱尺寸比第Ⅳ组小，因此，两者的爬高曲线必然不一样，最大爬高自然亦不一样，但给出的第Ⅲ组试验结果却与第Ⅳ组相仿，最大爬高也基本一致。在第Ⅳ组试验结果中，同时给出了Li 等、Zhao 等和孙忠滨等的计算结果，可以看到三者的结果与Isaacson 的试验和计算结果相比，偏差较大，相反，本文结果却吻合地很好，特别是与Isaacson 的解析计算结果吻合非常理想。这充分体现出本文对曲边界的处理是准确和合理的。图9 给出了本文计算波浪传播的透视图，可以明显地看出波浪在圆柱周围的绕射和在圆柱上的爬高，波面光滑、稳定，说明了本文模型的计算有很好的收敛性和稳定性。

3 结 语

基于Beji 的改进型方程，利用有限单元法建立了一个波浪数值模型。本模型的核心是建立了准确的曲边界计算方法，并配以速度分量同时在一个方程组求解的处理方法，利用高效的“重开始广义极小残量法”准确地求解曲边界的波浪计算问题，真正意义上体现出了有限单元法对曲边界求解的计算优势。

通过三个算例的模型验证，显现出了本文模型:1)能准确地模拟浅水非线性波浪;2)能在大面积水底地形变化的水域上，准确模拟波浪的折射、绕射;3)能对曲边界进行准确的计算。可见，本文模型是一个能有效而准确地适用于曲边界的浅水非线性波浪模型，能够应用于具有不规则边界的、海底变化的大面积水域波浪模拟等实际工程问题，也为椭圆余弦波与物体相互作用的进一步分析和研究工作提供了可靠的数值计算工具。

［1］PEREGRINE D H.Long waves on a beach［J］.Journal of Fluid Mechanics，1967，27:815－827.

［2］NWOGU O.Alternative form of Boussinesq equations for nearshore wave propagation［J］.Journal of Waterway，Port，Coastal and Ocean Engineering，1993，119(6):618－638.

［3］BEJI S，NADAOKA K.A formal derivation and numerical modeling of the improved Boussinesq equations for varying depth［J］.Ocean Engineering，1996，23(8):691－704.

［4］GOBBI M F，KIRBY J T.A fully nonlinear Boussinesq model for surface waves.Part 2:Extension to O(kh)4［J］.Journal of Fluid Mechanics，2000，405:181－210.

［5］MADSEN P A，BINGHAM H B，SCHäFFER H A.Boussinesq－type formulations for fully nonlinear and extremely dispersive water waves:derivation and analysis［J］.Proceedings of the Royal Society of London，Series A，2002，459:1075－1104.

［6］LI Y S，LIU S X，YU Y X，et al.Numerical modeling of Boussinesq equations by finite element method ［J］.Coastal Engineering，1999，37:97－122.

［7］WALKLEY M.A numerical method for extended Boussinesq shallow－water wave equations ［D］.Leeds:The University of Leeds，1999:110－132.

［8］ZHAO M，TENG B，LIU S X.Numerical simulation of improved Boussinesq equations by a finite element method［J］.Journal of Hydrodynamics，Ser.B，2003(4):31－40.

［9］孙忠滨，柳淑学，李金宣.基于改进Boussinesq 方程三角形网格有限元模型［J］.海洋工程，2010，28(3):50－58.(SUN Zhongbin，LIU Shuxue，LI Jinxuan.Triangular element FEM model based on modified Boussinesq equations［J］.The Ocean Engineering，2010，28(3):50－58.(in Chinese))

［10］ISAACSON M de St Q.Wave run－up around large circular cylinder［J］.Journal of the Waterway，Port，Coastal and Ocean Engineering，ASCE，1978，104(1):69－79.

［11］ENGELMAN M S，SANI R L.The implementation of normal and/or tangential boundary conditions in finite element codes for incompressible fluid flow［J］.International Journal for Numerical Methods in Fluids，1982，2:225－238.

［12］FENTON J D.The numerical solution of steady water wave problems［J］.Computers ＆ Geosciences，1988，14:357－368.

［13］WANG B L，LIU H.Higher order boussinesq－type equations for water waves on uneven bottom［J］.Applied Mathematics and Mechanics，2005，26(6):774－784.

［14］BRUSSINO G，SONNAD V.A comparison of direct and preconditioned iterative techniques for sparse，unsymmetric systems of linear equations［J］.International Journal for Numerical Methods in Engineering，1989，28:801－815.

［15］URSELL F.The long－wave paradox in the theory of gravity waves［J］.Proceedings of the Cambridge Philosophical Society，1953，49:685－694.

［16］BERKHOFF J C W，BOOY N，RADDER A C.Verification of numerical wave propagation models for simple harmonic linear water waves［J］.Coastal Engineering，1982，6:255－279.