涡旋澄清池沉淀区结构参数的固液两相流数值模拟

童祯恭，冯治华，童承乾，衷 诚

（华东交通大学土木建筑工程学院，江西 南昌330013）

涡旋澄清池由于其处理效果好、出水水质稳定、占地面积小以及排泥性能好等优点，具有较好的经济效益、社会效益及应用前景。Fluent软件是由美国Fluent公司于1983年推出的CFD软件，国内外许多专家学者应用CFD技术对各种水处理反应器流场进行了数值模拟，并取得了非常有价值的研究成果［1-3］。

文章应用Fluent软件对涡旋澄清池沉淀区进行三维数值模拟，采用标准k-ε两方程湍流模型和简化的双流体混合（Mixture）模型，建立了该沉淀区在不同结构参数下的流速场与悬浮物的分布，进而确定最优结构参数。

1 涡旋澄清池数值模型

两相流的研究存在两种观点：一种是把流体作为连续介质，而把颗粒群作为离散体系，即离散相模型；而另一种是既把流体作为连续介质，又把颗粒群当作拟连续介质或拟流体，即多相流模型。在Fluent多相流模型中［4-5］，将悬浮物（SS）颗粒作为连续介质，认为颗粒（固相）与流体同时存在且相互作用渗透，存在欧拉（Eulerian）模型、混合（Mixture）模型和VOF（volume of fluid）模型3种模型。其中，混合模型多用于两相流或多相流（流体或颗粒）。考虑到模拟对象颗粒（固相）分布广泛且体积分数超过10%，相间的曳力规律不明，计算机性能及几何模型复杂程度，采用混合模型。混合模型求解混合相的连续性方程、混合相的动量方程、混合相的能量方程、第二相的体积分数方程，还有相对速度的代数表达。

1.1 数学模型的建立

1.1.1 混合模型的连续性方程

建立混合模型的连续性方程

1.1.2 混合模型的动量模型

通过对所有相各自的动量方程求和获得混合模型的动量方程，可表示为

式中：n是相数；为体积力；μm为混合粘性，为第二相k的漂移速度；t为时间，s；为重力加速度。

1.1.3 混合模型的能量方程混合模型的能量方程采用如下形式

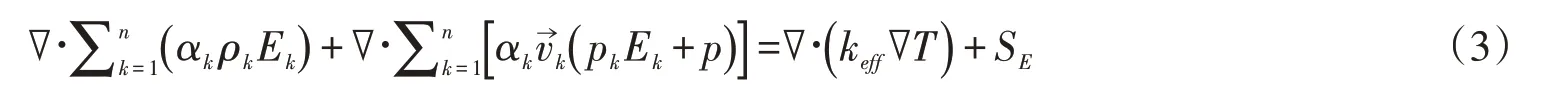
式中：keff为有效热传导率（keff=k+kt，这里的kt指湍流热导率，根据选定的湍流模型使用）。由于传导造成的能量传递右边添加第一项；SE包含了所有的体积热源；在方程中，，对应可压缩相；而Ek=hk是对应不可压缩相的，这里hk是第k相的显焓。

1.1.4 相对（滑移）速度和飘移速度相对速度（也称滑移速度）被定义为第二相（p）的速度相对于助相，漂移速度（）和相对速度（）的关系为

1.1.5 第二相的体积分数方程

从第二相p的连续方程，可以得到第二相p的体积分数方程为

1.2 模型的数值求解方法

流场数值求解本质上是对离散后的控制方程组的求解。采用有限体积法对方程进行离散求解，为使离散方程不会产生负系数及物理真实对流项采用UD（上风差分格式）近似，根据Patankar 和Spalding 于1972年提出的SIMPLE（压力耦合方程的半隐式法）算法求解［6-7］。

1.3 边界及初始条件

1.3.1 进水口条件

斜板沉淀区进口流速、悬浮物浓度采用均匀分布的假定，入口边界条件采用速度入口，对于液相入口速度v、湍流强度I及湍流长度尺度L按下面公式进行计算

式中：Q为入口流量，m3·s-1；A为入口面积，m2；ReDH为水力直径，为湿周，m。

1.3.2 自由面条件

斜板沉淀区出口断面为自由液面，忽略风引起的切应力及大气热交换，采用自由出流出口，出口压力为一个标准大气压。

1.3.3 固体边界条件

斜板沉淀区外围壁面、斜板、底部及挡板假定为固体壁面，即所有壁面处的节点没有相对滑移速度且湍动能和耗散率为0。

2 涡旋澄清池

采用华东交通大学孔目湖中水实验基地实际运行的涡流澄清池作为验证模型，利用上述建立的计算模型和数值求解方法对其实测值和计算值进行对比，从而调整模型的参数使得计算模型能够最大程度上符合实际情况。涡流澄清池基本参数如下：设计处理水量10 m3·h-1，絮凝反应时间6.8 min，水力停留时间32 min，清水区液面负荷5 m3·（m2·h）-1。其结构和尺寸设计如图1所示。

图1 涡旋澄清池结构图Fig.1 The structure of vortex coagulation

3 模拟结果及讨论

以华东交通大学孔目湖中水实验基地实际运行的涡流澄清池系统［8］作为验证实例。固相的初始速度与流体相的速度相同；依据Wells实验［9］及董红军模拟［10］选定入口悬浮固体浓度为1 081 kg·m-3；依据王晓玲等［11］结论假定颗粒可从进口截面均匀分布地进入沉淀池内。

文章采用的是三维数值模拟，而实验数据为二维，因此用模拟得到的悬浮物分布云图沿坐标轴z正向取平在x=0.8 m处的浓度值与Asgharzadeh H等［12］实测结果进行对比，见图2，其中C为悬浮物的浓度，C0为初始浓度。

由图2可知：模坐拟标轴z正向断面固相浓度值吻合较好，最大误差约为13%，从而验证了此模型能真实地反映涡流澄清池内固相的浓度分布。

图2 固相浓度计算值与实验值对比图Fig.2 Comparison of experimental and predicted solid phase concentration

3.1 网格划分

研究主要目的是考察涡旋澄清池斜板沉淀区及泥斗区的水场状态及出水污泥浓度，为减少不必要的计算量，简化模型如图3（a）所示。由于本模型具有复杂边界外型的流场，依靠Gambit默认最合适的网格划分算法，快速生成高精度的非结构混合网格如图3（b）所示，网格数为901 139个。

3.2 流场及悬浮物的分布

假定排泥管不排泥，水流以0.004 42 m·s-1的速度进入，得到的水流和悬浮物分布图见图4。图4（a）表明遇到下翻挡板绝大部分向下继续流动，越过挡板产生明显偏折，沿斜板向上流。由图4（b）可见进口处悬浮物浓度未发生明显变化，继而随着水流扩散，泥斗区、沉淀区以及斜板区积泥，泥斗区浓度最高；由于上升水流能将部分悬浮物带入清水区，继而随着水流上升势能增大流速降低，悬浮物受重力下沉，出口浓度最低。由此可表明建立的三维模型，能较为真实地反映涡旋澄清池的水流及悬浮物的分布。

图3 装置网格划分图Fig.3 Meshing of the device

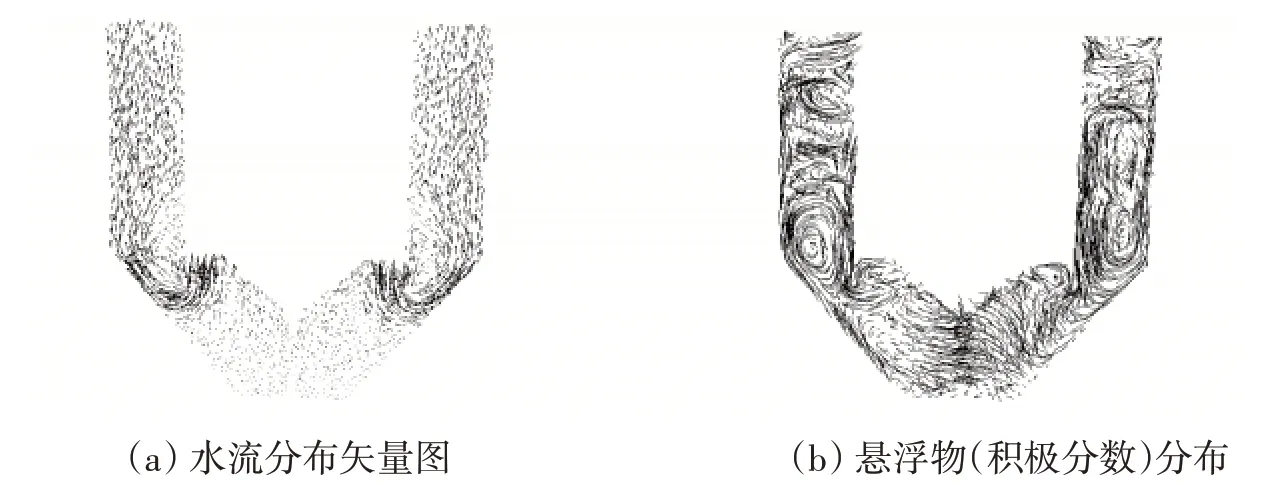
图4 z-y断面水流及悬浮物体积分数分布云图Fig.4 The distribution of flow field and suspended solids volume fraction at the section z-y

3.3 挡板长度的影响

图5模拟的是在斜板长1 m、倾角60°、间距70 mm时，挡板长度分别为100，200，300，400 mm的水流和悬浮物分布状况。图5（a）其悬浮物的体积分数分布云图表明，在安装不同浮渣挡板长度时有较大区别。受挡板长度影响，挡板愈长悬浮物越容易沉淀；而涡流澄清池泥斗处的悬浮物浓度分布受其影响强烈且随其增大而变浓，积泥增多。图5（b）其水流的速度值分布云图有较大变化。清水区水流速度受其长度影响波动较大的是200 mm，其后依次是300，400，100 mm；而斜板区则是100，400，200，300 mm；沉淀区与涡流澄清池泥斗区受挡板长度影响趋势较为一致，即100，200，400，300 mm。水流速度变化越大悬浮物越不容易沉降，因此挡板长度为300 mm时悬浮物沉降效果越好。

对不同挡板长度时悬浮物的去除效果进行分析计算，其结果见表1，可以得出在挡板长度为300 mm时对悬浮物的去除效果最佳。这与上述悬浮物的体积分数分布云图与水流的速度值分布云图分析结论一致。故以下模拟中浮渣的长度均选定为300 mm，挡板与进口垂直，且距第一反应室壁面200 mm。

表1 不同挡板长度时的去除效果Table 1 The removal rate with different baffle length

3.4 斜板间距的影响

图6模拟的是斜板长1 m、倾角60°、浮渣挡板长度300 mm时，斜板间距分别为70，55，40，35 mm时的水流和悬浮物分布状况。图6（a）其悬浮物的体积分数分布云图表明，不同斜板间距时有较大区别。受斜板间距影响，随斜板间距减小斜板区内斜板积泥量增多，当间距小于40 mm后板上积泥量减少；而澄清池泥斗内悬浮物浓度分布受其影响，间距为40 mm时积泥最多，随后为55，70，35 mm。由图6（b）可以发现，其水流的速度值分布云图有明显变化，尤其是在斜板下方的沉淀区内在斜板间距为40 mm流速较大、斜板间距为35 mm时波动较大，斜板间距为55 mm时流速最小、最为平稳；而在清水区与泥斗区内流速都有明显波动，但在斜板间距为55 mm时较平稳。模拟得出结论，斜板间距为55 mm时最有利于悬浮物沉降。

图5 流场内流体流态图Fig.5 Fluid flow chart of the flow field

图6 流场内流体流态图Fig.6 Fluid flow chart of the flow field

对不同斜板间距时悬浮物的去除效果进行分析计算，其结果见表2，可以得出在斜板间距为35 mm时对悬浮物的去除效果最佳。悬浮物的体积分数分布云图表明斜板间距55 mm较35 mm斜板上积泥多，但又较40 mm积泥量少；同时斜板间距为55 mm时最有利于悬浮物沉降；为保证斜板结构的稳定性、降低耗材，斜板间距最优工况为55 mm。故以下模拟中斜板间距均选定为55 mm。

表2 不同斜板间距时的去除效果Tab.2 The removal rate at different Inclined plate spacing

3.5 斜板倾角的影响

图7模拟斜板长1 m、挡板长300 mm、斜板间距55 mm时，斜板倾角为60°，50°，45°时的水流和悬浮物分布状况。图7（a）表明，在斜板区都具有明显积泥且60°泥量最少；进口至挡板深度区悬浮物浓度变化趋势很接近；在泥斗区悬浮物分布云图有较大区别，且45°浓度最大，随后为60°，50°。可见斜板倾角愈大愈有利板上积泥的滑落，增多与悬浮物吸附聚集地滑落积泥，进而促进沉淀。图7（b）表明，水流速度在清水区、斜板区、沉淀区以及泥斗区有明显变化。随着斜板倾角的减小涡流澄清池清水区增大，进而清水区水流变化明显。随着斜板倾角的增大涡流澄清池中水流发展的愈稳定，进而在倾角60°时，流澄清池中水流速度值分布云图变化较小。

图7 流场内流体流态图Fig.7 Fluid flow chart of the flow field of

对斜板间距时悬浮物的去除效果进行分析计算，其结果见表3。得出在倾角60°时对悬浮物的去除效果最佳。这与，上述悬浮物的体积分数分布云图与水流的速度值分布云图分析结论一致。但考虑到减小倾角可以加深涡流澄清池清水区、降低池体高度和能耗。故建议斜板倾角采用50°。

表3 不同斜板倾角时的去除效果Tab.3 The removal rate with different baffle length

4 结论与讨论

本文采用混合两相流模型对涡旋澄清池进行了三维数值模拟，得到主要结论如下。

1）标准k-ε两方程湍流模型和简化的双流体Mixture模型可以较好地模拟涡旋澄清池内速度场和污泥体积浓度的分布情况。

2）三维涡旋澄清池模型建立时考虑了挡板与污泥斗的影响，与涡旋澄清池实际物理模型相符。对模型z-y切面水流流场及悬浮物分布云图进行分析，发现流速与悬浮物分布受池底、边壁、斜板及挡板影响较大。这表明建立的模型能较好的反映水流及悬浮物的分布。

3）当斜板间距一定时，涡旋澄清池的去除率在一定范围内随着挡板长度的增大而增大，但挡板长度超过300 mm后悬浮物去除率减小，分析可能是挡板在一定长度范围内可促进沉降，超过临界后会阻碍污泥的下降。

4）挡板长300 mm、斜板倾角60°时，模拟70，55，40，35 mm 四种斜板间距对悬浮物去除的影响，表明随着斜板间距减小，悬浮物去除率明显逐渐增大，这与Hazen浅层沉淀理论相一致，进一步证明模拟结果的准确性。

5）挡板长300 mm、斜板间距55 mm时，模拟60°，55°，45°三种斜板倾角对悬浮物去除的影响，表明在倾角为60°时去除效果最佳，但从耗材与能耗方面考虑，建议斜板倾角采用50°。

[1]屈强,马鲁铭,王红武.辐流式二沉淀池固液两相流数值模拟[J].同济大学学报:自然科学版,2006,34(9):1212-1216.

[2]MATTHIEU D,JOSÉ V,ABDELLAH G.Experimental investigation and CFD modelling of flow,sedimentation,and solids separation in a combined sewer detention tank[J].Computers&Fluids,2009,38(5):1042-159.

[3]付立静,王军,陈胖胖.辐流式二沉池的数值模拟及应用[J].环境科学与管理,2010,35(8):64-67.

[4]雷晓玲,陈昆萍,陶礡.给水厂高密度沉淀池沉淀效果三维数值模拟与优化[J].中国给水排水,2012,28(1):43-47.

[5]SALIM S,GILISSEN L,RINZEMA A,et al.Modeling microalgal flocculation and sedimentation[J].Bioresource Technology,2013,144:602-607.

[6]魏文礼,张沛,刘玉玲.平流式沉淀池液固两相流力学特性的立面二维数值模拟[J].应用力学学报,2014,31(2):242-245.

[7]SARKAR S, KAMILYA D,MAL B C.Effect of geometric and process variables on the performance of inclined plate settlers in treating aquacultural waste[J].Water Research,2007,41(5):993-1000.

[8]童祯恭,闵凯,杨静芝.涡旋澄清池反应区数值模拟研究[J].华东交通大学学报,2013,30(2):16-20.

[9]WELLS S A,LALIBERTE D.Winter temperature gradients in circular clarifiers[J].Water Environment Research, 1998,70(7):1274-1279.

[10]董红军.基于FLUENT涡流澄清池斜管设计参数研究[D].南昌:华东交通大学,2012.

[11]王晓玲,孙蕊蕊,敖雪菲.大涡模拟在旋流沉砂池中的应用研究[J].工程力学,2013,30(8):155-162.

[12]ASGHARZADEH H, FIROOZABADI B, AFSHIN H.Experimental and numerical simulation of the effect of particles on flow structures in secondary sedimentation tanks[J].Journal of Applied Fluid Mechanics,2012,5(2):15-23.