钢筋混凝土拱桥极限承载力的参数分析

陈定市，胡大琳，胡 伟，张 凯

（长安大学公路学院，陕西 西安710064）

钢筋混凝土拱桥由于造型美观、承载力高等优点在国内外被广泛使用，特别是在山区与海岛的建设中仍有着广阔的应用前景，同时已建成的大量钢筋混凝土拱桥也需要养护、维修、加固与改造［1～3］。

目前进行钢筋混凝土拱桥极限承载力的研究方法主要有模型试验和数值分析两种。郑振飞、陈克济、陈宝春等进行了模型试验研究且得到了类似的结论，即无铰拱和两铰拱分别在形成4个塑性铰和2个塑性铰后，结构成为机构而破坏。郑振飞［4-5］、陈克济等［6］应用杆系单元有限元程序，对拱的面内极限承载力进行了双重非线性的分析，考虑了截面上混凝土开裂引起的应力重分布和塑性铰形成后的内力重分布现象。陈宝春［7］采用平面分离式单元，考虑材料非线性和裂缝对结构受力的影响，改善了计算收敛的问题，但内存要求高。胡大琳［8-9］采用平面框架单元考虑双重非线性分析拱的几何非线性和极限承载力，改善了杆系单元双重非线性分析的效率与精度。邓莉［10］、李松等［11］用通用程序ANSYS进行了钢筋混凝土拱的非线性分析。

由于双重非线性分析的复杂性，目前数值分析方法仍主要局限于研究之中，实际工程多采用简化算法。简化算法主要有基于弹塑性失稳理论的等效梁柱法和基于刚塑性理论的极限分析法两大类。等效柱法考虑的是理想的纯压拱，无法考虑弯矩、结构初始缺陷等影响，适用于长细比比较大钢筋混凝土拱桥。极限分析法基于结构形成了塑性铰成为机动体系，而此时第一个塑性铰的裂缝宽度已得到极大的开展，远超出使用极限状态的要求，且此法没有考虑P-δ效应，一般适用于结构承受弯矩较大的机构破坏模式，迄今未被设计规范所采用。

从理论上讲，钢筋混凝土拱不计其钢筋的作用而采用圬工规范进行计算，应该是偏于安全的。然而，笔者在计算马蹄河特大桥时发现采用两种规范的计算结果存在矛盾之处，采用《公路圬工桥涵设计规范》（JTG D61-2005）［12］验算能通过，而采用《公路钢筋混凝土及预应力混凝土桥涵设计规范》（JTG D62-2004）［13］验算不能通过，对钢筋混凝土偏压柱和一些试件的进一步验算分析，结果表明两本规范中砌体、素混凝土或钢筋混凝土偏压柱的承载力算法存在类似的不合理的现象，文献［14］也得出类似的结论。另外，与美国［15］和日本［16］桥梁设计规范相比，我国规范采用等效梁柱法时没有考虑矢跨比的影响。由于各规范关于拱圈等效长度的取值存在一些差异，因此按照各规范计算的拱圈承载力结果也存在差异，拱圈等效长度的合理取值有待进一步研究。

大跨径钢筋混凝土拱桥的极限承载力受多种非线性因素的影响，采用常规的简化算法不能反映结构的真实受力状态，而按现行规范［12-13］的计算结果与结构的真实承载力有较大差异。因此，对钢筋混凝土拱桥的极限承载力进行参数研究，找到主要的影响参数及各参数的影响规律，必将为钢筋混凝土拱桥的理论研究、设计及施工提供可靠依据。

1 工程概况及有限元模型

马蹄河特大桥地处贵州省中北部，桥跨布置为2×30 m预制T梁+净跨180 m主拱+2×30 m预制T梁，全桥长327.595 m。主桥为等截面悬链线钢筋混凝土无铰拱桥，主拱净跨径180 m，净矢高32 m，拱轴系数1.988。主拱圈采用单箱双室截面，高3.3 m，宽7.5 m。桥梁设计荷载为公路-I级。桥面系由8片预应力混凝土简支空心板构成，每片空心板的跨度为13 m，梁高为70 cm，为先简支后桥面连续结构。该桥行车道宽度为2×净-9.625 m，设计的基准期为100年，设计车速为80 km·h-1。拱上设立柱或者整体式盖梁共14道。主拱圈和预应力混凝土简支空心板使用C50混凝土，拱座、拱上垫梁、拱上排架、系梁和盖梁均使用C40混凝土。

采用通用有限元软件ANSYS建立空间有限元计算模型，全桥共划分单元3 353个。主拱圈、底梁、拱上立柱、立柱之间的横系梁和盖梁均采用BEAM188单元来模拟，上部结构的桥面系采用释放转角自由度的BAEM44单元来模拟，连接系采用空间梁单元BAEM4模拟。值得说明的是，为了考虑拱上结构的联合作用，本文计算采用全桥模型，但主要考虑主拱圈的受力行为。有限元模型如图1所示。

图1 三维有限元模型Fig.1 Three-dimensional finite element model

钢筋混凝土拱的极限承载力分析应考虑几何非线性和材料非线性的影响，本文混凝土材料本构关系采用美国学者Hongnested提出的应力-应变曲线模型［17］，如图2所示。基本构方程为：

式中：ε0=2σ0/E0，是达到最大压应力时对应的混凝土压应变，其中E0是混凝土受压的初始弹性模量，σ0取混凝土标准圆柱体抗压强度的0.85倍；εu是混凝土的极限压应变，理论分析时取0.0038。由于混凝土的抗拉强度很小，对结构的极限承载能力影响很小，本文在混凝土应力-应变关系的模拟中忽略混凝土的抗拉能力。钢筋的本构关系可简化为理想弹塑性材料，其应力应变关系曲线如图3所示。求解采用完全的牛顿-拉夫逊迭代法，以位移增量来判断收敛的标准，迭代收敛必须满足如下条件：

式中：αd为位移收敛容差；‖ Δui+1‖为位移增量向量的某种范数。

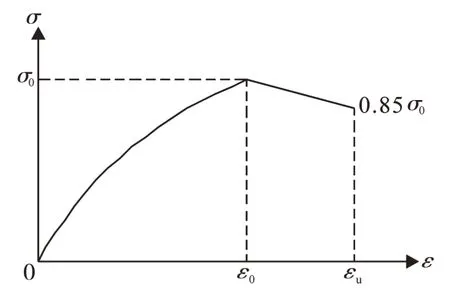
图2 混凝土的应力-应变曲线Fig.2 Stress-strain curve of the concrete

图3 钢筋的应力-应变曲线Fig.3 Stress-strain curve of the steel

2 荷载分布方式对拱桥极限承载力的影响

活荷载采用公路-Ⅰ级车道荷载，取均布荷载的标准值为10.5 kN·m-1，集中力荷载的标准值为360 kN。有限元计算时先施加恒载并保持其值不变，然后施加活荷载，活荷载按照初始的公路-Ⅰ级车道荷载成比例增加的方式施加。定义活荷载系数=当前活荷载组合/初始活荷载组合，根据活荷载的加载位置分为3种荷载工况：①工况1——恒载+全桥均布活荷载（集中力荷载在跨中）；②工况2——恒载+半幅桥全跨均布活荷载（集中力荷载在跨中）；③工况3——恒载+半跨均布活荷载（集中力荷载在L/4处）。不同荷载工况下的计算结果见表1，与集中力荷载作用位置对应的荷载-位移曲线如图4所示。

表1 不同加载方式对拱桥极限承载力的影响Tab.1 Effects of loading modes on the ultimate bearing capacity of arch bridge

由表1和图4可见，该桥在工况1 下达到极限荷载时的活荷载系数为44.601，此时拱顶的竖向位移为0.813 m；在工况2下达到极限荷载时的活荷载系数为31.828，比工况1减小了28.6%，此时拱顶的竖向位移为0.636 m；而工况3下结构达到极限荷载时的活荷载系数为17.293，比工况2减小了45.7%，比工况1减小了61.2%，此时1/4拱圈处的竖向位移为0.712 m。结果表明，与全桥均布活荷载相比，半幅桥全跨均布活荷载和半跨均布活荷载的加载方式使结构的极限承载能力会更低，其中半跨均布活荷载对结构极限承载力的影响更为明显。所以，对大跨度的钢筋混凝土拱桥，活荷载的加载方式是影响其极限承载力的一个关键因素。

图4 不同加载方式下的荷载-位移曲线Fig.4 Load-displacement curve under different loading modes

从该桥塑性区域的出现顺序和最终的破坏形式来看，当活荷载采用工况1的加载方式时，拱顶截面材料首先发生屈服，然后塑性区域相继在两个拱脚截面附近出现，随着荷载的不断增大，当在1/4拱圈和3/4拱圈截面处也形成塑性区域时，结构达到极限荷载，趋于形成可变机构，最终导致结构以面内正对称的形式破坏；当活荷载采用工况2的加载方式时，塑性区域的形成顺序与工况1基本相同，最终的破坏形式也为面内正对称，只是活荷载系数较工况1的情况下减小了28.6%；而当活荷载采用工况3的加载方式时，随着荷载的不断增加，塑性区域的出现顺序为：远离荷载作用侧的拱脚截面处——荷载作用侧的1/4拱圈截面处——荷载作用侧的拱脚截面处——远离荷载作用侧的1/4拱圈截面处，结构最终的破坏形式变为面内反对称。

上述分析结果表明，荷载分布方式不仅影响结构从加载开始直至破坏的发展过程，还会影响结构的最终破坏形式。

3 结构设计参数对拱桥极限承载力的影响

3.1 拱圈混凝土强度的影响

强度等级的改变意味着混凝土屈服应力的改变，而屈服应力是衡量材料非线性行为的一个重要指标，因此，必然会对结构的极限承载力造成影响。以下就混凝土强度等级取C45～C65时，对结构极限承载能力的影响进行了分析，计算结果见表2和图5，拱顶处的荷载-位移曲线如图6所示。

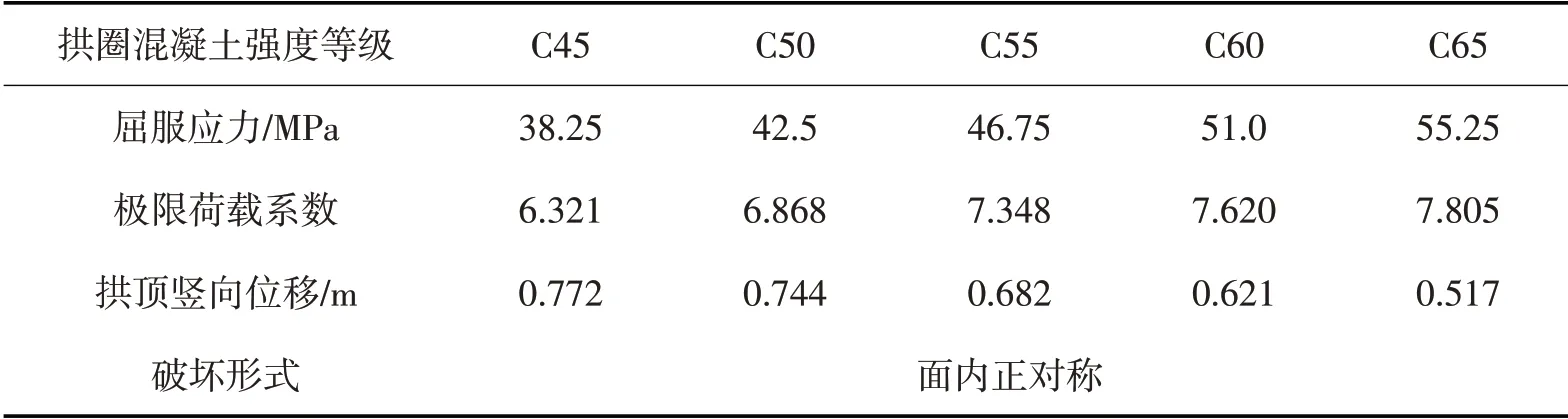
表2 拱圈混凝土强度对拱桥极限承载力的影响Tab.2 Effects of concrete strength of the arch ring on the ultimate bearing capacity of arch bridge

图5 拱圈混凝土强度与结构极限荷载系数的关系曲线Fig.5 Relationship between the concrete strength and the ultimate load coefficient of the main arch

图6 不同混凝土强度下拱顶的荷载-位移曲线Fig.6 Load-displacement curves of different concrete strength at the arch crown

从以上计算结果中可以看出随着混凝土强度等级的提高，结构的极限荷载系数也随着增大，结构能承受的极限荷载逐渐增强。也反映了材料屈服强度越高，结构的刚度就越大，结构进入塑性的状态也就越晚。当混凝土的强度等级从C45变化到C55时，结构的极限荷载系数由6.321变化到7.348，增加了15.0%，且曲线基本呈线性增长。而当混凝土强度等级从C55变化到C65时，结构的极限荷载系数由7.348变化到7.805，只增加了5.8%。表明随着拱圈混凝土强度等级的提高，结构的极限承载能力提高速率在减小。

从拱顶处的荷载-位移曲线图来看，随着拱圈混凝土的强度等级从C45提高到C65时，结构在达到极限荷载时的拱顶竖向位移却减小了，表明结构的延性有所降低。因此，在实际设计中，应避免盲目采用过高的混凝土强度等级来追求高的结构极限承载能力，因为这可能导致结构发生脆性破坏。

3.2 拱圈面内抗弯刚度的影响

通过改变拱圈的面内抗弯刚度，使其在原设计值的基础上分别减小20%、减小40%和减小60%，然后分析其对结构极限承载力的影响。由于马蹄河特大桥的截面是等高度的，可以方便地通过调整其截面高度来实现其抗弯刚度的改变，计算结果见表3和图7，拱顶处的荷载-位移曲线如图8所示。

表3 拱圈面内抗弯刚度对拱桥极限承载力的影响Tab.3 Effects of in-plane stiffness of the arch ring on the ultimate bearing capacity of arch bridge

图7 拱圈面内刚度对结构极限荷载系数的影响Fig.7 Influence of the in-plane stiffness on the ultimate load coefficient

图8 不同拱圈面内抗弯刚度下拱顶的荷载-位移曲线Fig.8 Load-displacement curves of different in-plane stiffness at the arch crown

由以图7和图8可知，当拱圈的面内抗弯刚度减小到原设计值的20%时，结构的极限荷载系数降低了3%，相应的拱顶竖向位移值增加了5.9%；当拱圈的面内抗弯刚度减小到原设计值的40%时，结构的极限荷载系数降低了9.2%，相应的拱顶竖向位移值增加了10.6%；当拱圈的面内抗弯刚度减小到原设计值的60%时，结构的极限荷载系数降低了21.8%，相应的拱顶竖向位移值增加了17.4%。结果表明，随着拱圈面内抗弯刚度的减小，相应的极限荷载系数值降低，达到极限荷载时的拱顶竖向位移值增大，拱圈的面内抗弯刚度是影响结构承载力，尤其是面内承载力的主要因素。

3.3 矢跨比的影响

矢跨比作为拱桥的主要设计参数之一，会直接影响到拱圈的受力状态。理论分析表明，矢跨比越小（结构表现为坦拱），拱脚处的水平推力就越大，相应拱圈的轴力也就越大。对大跨度拱桥而言，结构的面内外刚度会严重地受到拱圈轴力大小的影响。以下就矢跨比在1/4.5～1/6.5范围取值时，对结构极限承载力的影响进行了研究，计算结果见表4和图9，拱顶处的荷载-位移曲线如图10所示。

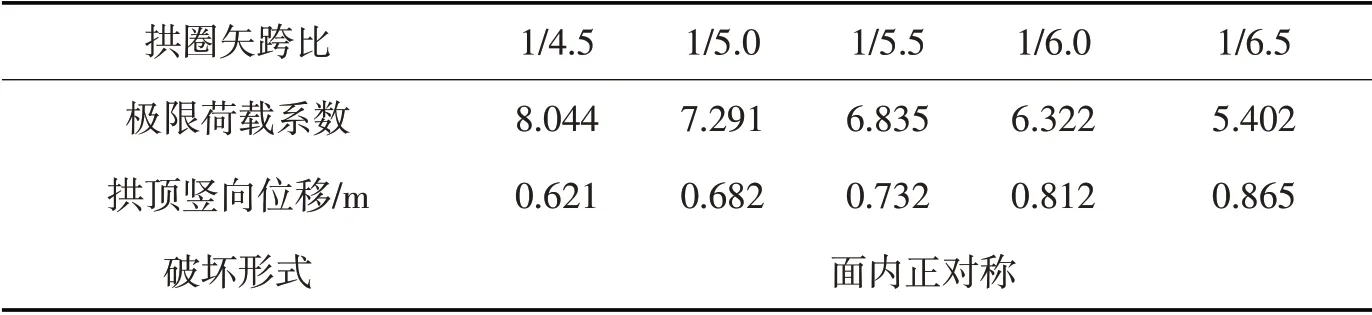
表4 矢跨比对拱桥极限承载力的影响Tab.4 Effects of rise-span ratio on the ultimate bearing capacity of arch bridge

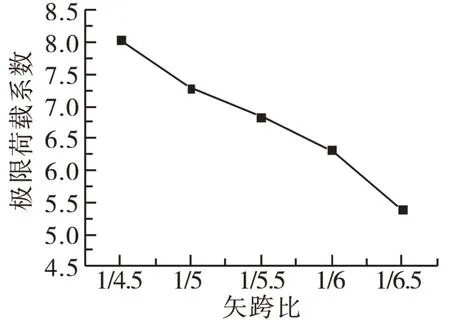
图9 矢跨比与结构极限荷载系数的关系曲线Fig.9 Relationship between the rise-span ratio and structural ultimate load coefficient

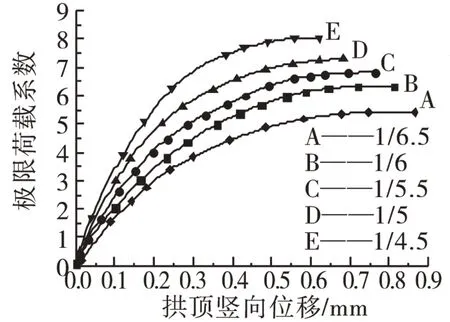
图10 不同矢跨比下拱顶的荷载-位移曲线Fig.1 0 Load-displacement curves of different rise-span ratio at the arch crown

表4和图9、图10表明，随着矢跨比的减小，相应的极限荷载系数值降低，达到极限荷载时的拱顶竖向位移值增大。当该桥的矢跨比在1/4.5～1/5.0 和1/6.0～1/6.5 这两个区间段变化时，结构的极限荷载系数分别下降了9.4%和15.6%，相应的拱顶竖向位移值分别增加了8.9%和6.1%，在图5、图6的关系曲线上可以明显看出这两个区间段曲线下降的比较快。而在矢跨比在1/5.0～1/6.0变化时，相应的极限荷载系数值下降的比较小，曲线变化也比较缓慢。当矢跨比为1/6.5 时，结构的极限荷载系数值只有5.402，比矢跨比为1/4.5 的极限荷载系数减小了67.2%，而且达到极限荷载时的拱顶竖向挠度值增加了。可见，该桥的矢跨比在1/5.0～1/6.0 之间取值时较为合适，马蹄河特大桥的矢跨比实际取值为1/5.625，正是在此合理区间范围之内。

4 初始几何缺陷对拱桥极限承载力的影响

实际结构都会或多或少存在各种不同程度的缺陷，缺陷主要有几何缺陷和力学缺陷两大类。拱桥的几何缺陷是成桥状态下的拱轴线与设计轴线不相符合，使得主拱圈在面、内外发生了初始变形，引起几何初始缺陷的原因主要有工厂制造过程中发生了偏差、运输过程中结构发生了损伤和施工过程中的不正确操作等，而力学缺陷是在没有承受荷载前，结构就存在了残余应力。理论计算分析和试验研究均表明，初始几何缺陷能对结构的承载力产生不能忽视的影响，而且这种初始的几何缺陷具有非常大的随机性，本文计算时以该桥在恒载作用下发生的面内和面外弹性屈曲的一阶屈曲模态作为初始扰动，分析几何初始缺陷对拱桥极限承载力的影响。取面内初始扰动分别为L/5 000，L/4 000，L/3 000，L/2 000和L/1 000，面外初始扰动分别为L/8 000，L/7 000，L/6 000，L/5 000和L/4 000，其中L为拱桥跨径，计算结果分别见表5和表6。

表5 面内初始缺陷对拱桥极限承载力的影响Tab.5 Effect of in-plane initial geometrical imperfections on the ultimate bearing capacity of arch bridge

表6 面外初始缺陷对拱桥极限承载力的影响Tab.6 Effect of out-plane initial geometrical defect on the ultimate bearing capacity of arch bridge

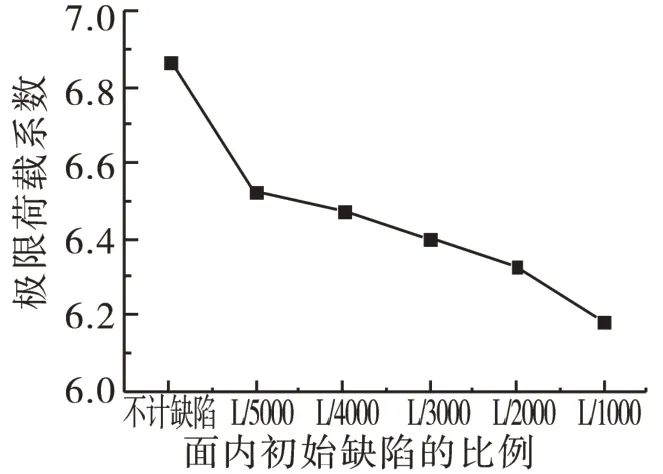
图11 面内初始缺陷与极限荷载系数的关系曲线Fig.1 1 Relationship between the in-plane initial geometrical imperfections and structural ultimate load coefficient

图12 面外初始缺陷与极限荷载系数的关系曲线Fig.1 2 Relationship between out-plane initial geometrical defect and structural ultimate load coefficient

从表5和表6可以看出，当存在L/1 000的面内初始缺陷时，结构的极限荷载系数为6.186，与无初始缺陷相比减小了9.9%；当存在L/4 000的面外初始缺陷时，结构的极限荷载系数为6.801，与无初始缺陷相比减小了1.0%，表明初始缺陷会使拱桥的极限承载能力降低，但降低的幅度不大。

从图11和图12可以看出，该桥在存在较小的面内初始缺陷时，极限荷载系数下降的比较明显，但随着面内初始缺陷值的增大，极限荷载系数下降缓慢；而计入面外初始缺陷后，极限荷载系数基本无明显的变化，说明该桥的极限荷载系数受面内的破坏模式控制。此外，受几何初始缺陷的影响，该桥在达到极限承载力时，结构的破坏形式也发生了不同程度的改变，考虑面内初始缺陷的影响后，该桥最终破坏由原来的面内正对称形式变为面内反对称形式，这是因为结构受到荷载作用后，其几何形状不完善，产生了与几何缺陷相适应的变形，导致最终破坏形式往往与不计缺陷影响的结果不同。

5 结论

本文以一座上承式钢筋混凝土拱桥——马蹄河大桥为工程背景，通过对活荷载的加载方式、拱圈混凝土的强度、拱圈面内的抗弯刚度、矢跨比和初始几何缺陷等参数对大跨度钢筋混凝土拱桥的极限承载力进行了分析，得出如下结论：

1）对刚度相对较大的钢筋混凝土拱桥，初始几何缺陷会降低结构的极限承载能力，但降低的程度很小，一般情况下可以忽略该参数的影响。

2）拱圈混凝土的强度、拱圈面内的抗弯刚度和矢跨比是决定大跨度钢筋混凝土拱桥极限承载力的3个关键设计参数，这些参数的正确选择，有助于改善结构的极限承载能力。

3）活荷载的不同加载方式在很大程度上影响了拱桥的极限承载能力，半跨均布活荷载下的极限承载力明显低于全桥均布活荷载下的极限承载力。

4）对大跨径的钢筋混凝土拱桥，其极限承载力会随着拱圈混凝土强度和拱圈抗弯刚度的增减而增减。

5）矢跨比在1/4.5～1/6.5之间取值时，随着矢跨比的降低，钢筋混凝土拱桥的极限承载能力也随之减弱，从减弱幅度来看，当该桥的矢跨比在1/4.5～1/5.0和1/6.0～1/6.5这两个区间段变化时，曲线下降的比较快；而在矢跨比在1/5.0～1/6.0变化时，相应的极限荷载系数值下降的比较小，曲线变化比较缓慢，表明此类桥的矢跨比在1/5.0～1/6.0之间取值时较为合适。

[1]陈宝春,叶琳.我国混凝土拱桥现状调查与发展方向分析[J].中外公路,2008(2):89-96.

[2]韦建刚,陈宝春.国外大跨度混凝土拱桥的应用与研究进展[J].世界桥梁,2009(2):4-8.

[3]陈宝春,林上顺.钢筋混凝土拱极限承载力研究综述[J].福州大学学报:自然科学版,2014(2):282-289.

[4]郑振飞,张尚杰,彭大文,等.钢筋混凝土拱的极限承载能力试验研究[J].福州大学学报:自然科学版,1982(2):79-90.

[5]郑振飞,彭大文.超静定钢筋混凝土拱的非线性分析[J].福州大学学报:自然科学版,1985(2):116-127.

[6]陈克济.钢筋混凝土拱桥面内承载力的非线性分析[J].桥梁建设,1983(1):24-36.

[7]陈宝春.钢筋混凝土无铰拱非线性平面有限元分析[D].福州:福州大学,1986.

[8]胡大琳.钢筋混凝土拱的非线性分析[J].华东公路,1992(3):77-81.

[9]胡大琳,陈祥宝.拱式拱上结构钢筋混凝土拱桥极限承载力分析[J].西安公路学院学报,1994,14(4):19-27.

[10]邓莉.在役钢筋混凝土拱桥承载潜力研究[D].西安:长安大学,2006.

[11]李松,强士中,唐英.钢筋混凝土拱桥极限承载力的参数研究[J].西南交通大学学报,2007,42(3):293-298.

[12]中华人民共和国交通部.JTGD62-2004 公路钢筋混凝土及预应力混凝土桥涵设计规范[S].北京:人民交通出版社,2004.

[13]中华人民共和国交通部.JTGD61-2005 公路圬工桥涵设计规范[S].北京:人民交通出版社,2005.

[14]LIN SHANG SHUN, CHEN BAO CHUN, WU QING XIONG.Discussion on calculation methods for load bearing capacity of concretearch bridge[C]//Fourth International Conference on Digital Manufacturing and Automation,2013:492-496.

[15]美国各州公路和运输工作者协会AASHTO.美国公路桥梁设计规范[M].辛济平,等译.北京:人民交通出版社,1998.

[16]JAPAN ROAD ASSOCIATION.Specifications for highway bridges,part III:concrete bridges[S].2002.

[17]何政,欧进萍.钢筋混凝土结构非线性分析[M].哈尔滨:哈尔滨工业大学出版社,2007.