基于Shapley值的竞争闭环供应链协调策略研究

2015-11-22郭军华杜言航

华东交通大学学报 2015年2期

郭军华，杜言航

（华东交通大学经济管理学院，江西南昌330013）

随着闭环供应链概念的提出，越来越多的企业已经关注废旧产品的回收。在转变经济发展方式的重要阶段，我国也通过立法的形式，要求企业承担更多的责任，加强废旧品的回收、再制造。企业在回收、再制造过程中不仅能获得更高的经济效益，同时也能提高企业自身形象。

近些年来，关于闭环供应链的定价和协调的文献有很多。比如：国外学者Gudie等人对闭环供应链的研究进行了文献综述，并提出将来的研究方向［1］。国内学者张诚同样也对供应链方面的论文进行了综述，研究结果表明，现有文献的侧重点有所不同，从对象、方法以及行业等方面对不同的实际情况进行深入研究［2］。颜荣芳，程永宏，王彩霞等研究了集中式决策和分散决策条件下再制造闭环供应链的差别定价问题［3］。公彦德和李帮义重点分析了由零售商主导和第三方物流服务商主导的两类供应链模型，得出后者的系统效率最高，并提出基于机会成本的协调方法［4］。公彦德研究了不同回收模式的闭环供应链，运用博弈论的方法，求解最优定价以及协调方法。文献［5］还研究了回收补贴对闭环供应链的影响，提出了新的解题思路。R.Canan Savaskan等人的研究基于闭环供应链的概念，提出由制造商回收、零售商回收、第三方回收3种回收渠道，并对3种回收渠道的闭环供应链进行比较，提出两部定价协调契约［6］。唐秋生等运用Stackelberg博弈理论制定数量折扣模型以解决网络直销和传统销售渠道的冲突并根据成员企业在系统中的重要程度分配系统利润，达到协调、优化的目的［7］。孙浩和达庆利运用两种决策方式研究了两周期再制造闭环供应链模型，并通过运算得出最优决策，利用收益共享契约对系统进行协调，通过仿真验证结论的正确性、可行性［8］。邱若臻建立以制造商为领导者，零售商为跟从者的Stackelberg博弈模型，分析了需求信息共享与否两种情形下最优定价。通过数值仿真，研究了各参数对系统及成员企业利润的影响［9］。林欣怡等人研究基于零售商竞争建立两周期的分散决策模型和集中决策模型，得出最优定价策略，并通过收益共享契约实现闭环供应链的协调［10］。王文宾和达庆利对消费者市场进行细分，建立由零售商回收和第三方回收两种闭环供应链决策模型［11］。王文宾等基于单一制造商和单一零售商组成的闭环供应链，分析不同渠道权力下决策变量和系统总利润，并运用两部定价策略对系统进行协调［12］。赵晓敏等对单一制造商和单一零售商构成的S-M两级闭环供应链，采用博弈论的方法研究最有定价策略，并比较不同模型的系统绩效［13］。郑克俊在零售商回收的模型基础上，运用博弈论的方法，制定再制造产品和新产品以及回收废旧品的最有定价策略，并对系统协调，达到更高的绩效［14］。易余胤建立了制造商领导、零售商领导、制造商和零售商共同领导的3种博弈模型，研究了3种不同市场力量结构对系统决策的影响［15］。张成堂等人的研究基于双渠道的闭环供应链模型，对比两种不同的决策模式，得出集中决策模式下的闭环供应链系统最优，并基于此提出一种新的协调方法［16］。从现有文献可以看出，无论建立的模型如何，都涉及到对闭环供应链的系统协调问题，因此下面介绍供应链的协调对策研究。

供应链协调的方法有很多种，运用Shapley值法对闭环供应链系统进行协调，关于此种协调方式的论文也有很多：吴美容等人在原有的Shapley解的基础上，提出新的方法能够更准确地描述经济现象，同时，将新方法运用到供应链系统利益协调分配的实际问题中［17］。李永飞等人建立合作环境下的矩阵博弈模型，重点运用Shapley值法对模型进行研究分析，最终通过数值分析验证结论，证实Shapley值法的可行性［18］。蒋永锋的研究基于合作博弈模型，证实利益分配需要考虑众多因素，而改进的Shapley 值法具有可操作性、可行性。在实际的分配过程中，能够获得系统中各主体接受，实现共赢［19］。刁丽琳等人认为传统的Shapely 值法在解决利润分配方面，考虑因素过于单一，因此会存在可操作性问题。在此基础上，通过加入各主体议价能力和对系统贡献等权重因子，提出多权重的Shapley值模型［20］。魏学成和李文涛认为公平合理的利益分配机制对供应链的成功运行至关重要，因此选择合适的分配方法使得各企业都能够主动接受、实现共赢才能使供应链系统高效运作。将综合修正因子引入传统的Shapley 值法就能够切实解决上述问题［21］。综上所述，Shapley值法作为一种协调方法，能够解决闭环供应链系统的利润分配问题。

本研究与上述文献的不同之处在于，在原先的闭环供应链中考虑制造商行业间的竞争，同时，基于不同决策模式求解模型的最优定价策略并比较，得出结论：相较与集中决策模式下，零售商领导的竞争闭环供应链在分散决策模式下的销售价格更高、回收价格更低、系统收益更低。因此，闭环供应链系统能够实现帕累托改进，运用Shapley值法对系统中的3个节点企业进行协调。最后通过数值分析证实协调策略的可行性，并且探讨价格敏感系数对制造商利润、零售商利润和系统总利润的影响。

1 符号说明与基本假设

1.1 模型

文献［5］提出3种不同的回收渠道，通过研究论证得出：当零售商负责回收时，系统总利润最大。因此，采取零售商负责回收模式：对于零售商回收而来的产品，制造商全部接受并且支付每单位废旧产品一定的价格，模型如图1所示。

1.2 基本假设

1）本模型由两个寡头制造商M1，M2和一个零售商R组成的两级闭环供应链，两个制造商提供的产品相似，具有相同的性质和功能，但是不可完全替代。两个制造商之间自由竞争。

2）在此模型中，制造商Mi既可以使用原材料进行生产，同时也可以利用回收产品进行再制造，成本分别为ci和cir。在这里假设cir＜ci，因此，在使用回收产品进行再制造的成本低于使用新材料进行生产的成本，制造商才有回收产品进行再制造的内在动力［5］。

3）制造商与零售商之间的信息是完全的，即市场的需求量等于零售商向制造商的批发量。因此，零售商不存在由于产品过多带来的库存费用和缺货造成的损失［7］。

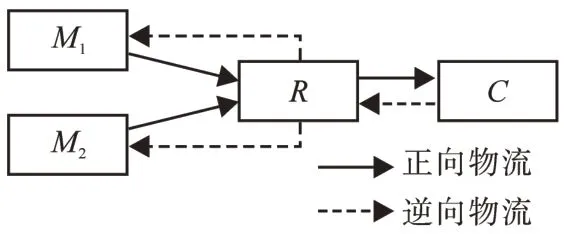
图1 零售商负责回收的闭环供应链模型Fig.1 Model of closed loop supply chain based on retailer’s recovery

4）本研究中，制造商和零售商均为风险中性［8］。

5）市场上对于两种产品的需求函数为qi=Q-pi+apj，其中i+j=3,i=1,2。Q为市场上对两种产品的基本需求；a表示某种产品对竞争产品的价格敏感程度(a＜1)［12］。

6）两种废旧产品的回收量函数为qir=φ+pir-βpjr，其中i+j=3,i=1,2。φ表示每种产品固定回收量，此部分与回收价格无关，反应社会的环保意识；β表示价格敏感程度(β＜1)［15］。

7）零售商回收的废旧产品全部可以用于再制造［17］。

1.3 符号假定

表1 各种符号的意义Tab.1 Significance of symbols

为使研究分析有意义，文中出现的各参数必须满足{i=1,2}：{pir≤pir+cr≤Δi≤ci≤wi≤wi+cr≤pi,qir≤qr}。

2 分散决策模型

假设零售商领导的竞争闭环供应链模型，因此零售商享有优先的渠道权利。整个闭环供应链的博弈顺序如下：①零售商基于利润最大化的原则，制定最优零售价格和回收价格(p1,p2,p1r,p2r)。②制造商确定最优的采购价格和最优回收价格(w1,w2,b1,b2)。假设制造商的批发价格为wi，则零售商的单位产品利润为mi=pi-wi-cr。同理，零售商的每单位回收产品的利润为ni=bi-pir-cr。数学模型如下{i=1,2}：

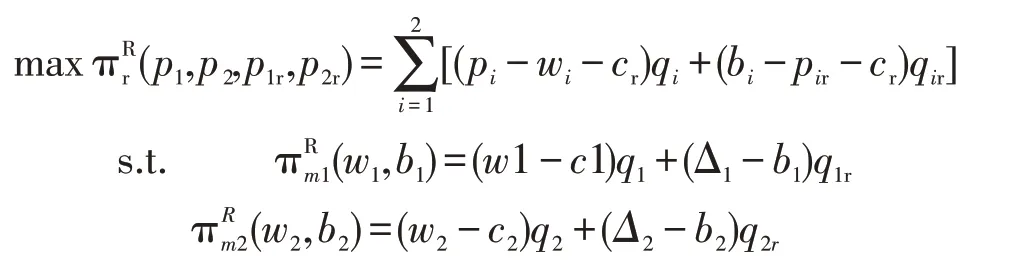
对于上述规划问题，采用逆向归纳法可得

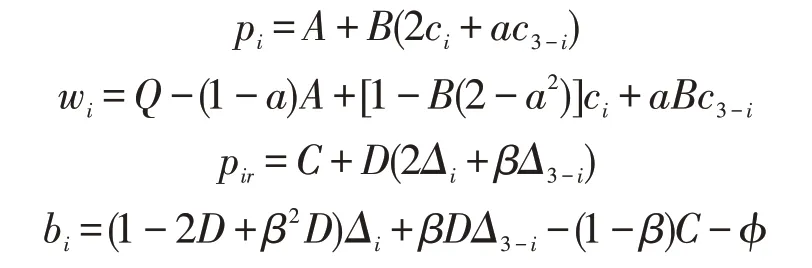
其中

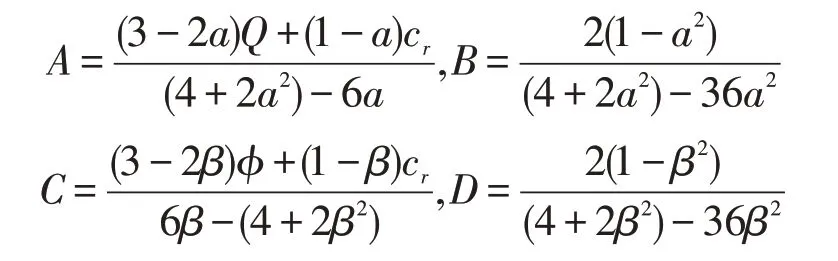
结论1当c1=c2时，即两个制造商生产新产品的成本相等，在零售商领导的竞争闭环供应链中，有p1=p2,w1=w2,q1=q2。同理可得，当Δ1=Δ2时，废旧产品的回收价格和转移价格相同，p1r=p2r,b1=b2,q1r=q2r。

结论1说明当两个寡头厂商垄断市场，且两个寡头厂商之间是自由竞争的，不存在行业领导者和跟踪者的区别，产量之间的竞争完全取决于两者成本之间的竞争。当两者的生产成本相同，而且价格替代系数也相等时，产品的批发价格和最终零售价格都相等。因为产品的需求量和价格以及竞争品价格有关，当两者价格相同时，产品的销售量也相等。同理，在废旧产品回首的过程中，结论必然成立。

3 集中决策模型

集中决策模型将闭环供应链中所有的节点企业当成一个理想化的“超组织”。此时系统所要确定的变量只有产品的零售价格和废旧产品的回收价格，而批发价格和回收转移价格仅仅决定系统最优化时各节点企业之间的利润分配，并不会影响系统的总利润。

决策模型如下：

由上式分别对决策变量(p1,p2,p1r,p2r)求一阶偏导，并令其等于0，联立方程式求解得出{i=1,2}，计算结果见表2所示。

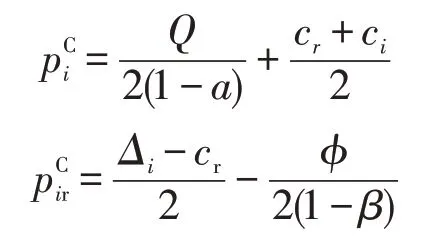
结论2由上式可知，当c1=c2=c时，同理可得，当Δ1=Δ2=Δ时，并且结合结论1的内容可得相对应的产品销售量和废旧产品的回收量有如下关系：

表2 不同决策模式下销售量和回收量Tab.2 Sales and recovery capacity under different decisions

结论2表示在集中决策模式下制定的最优零售价格是最低的，但是回收价格却是最高的。因为集中决策将闭环供应链作为一个有机整体，有效消除分散决策中存在的“双重边际效应”和“牛鞭效应”，在传统的正向供应链中降低零售价格以获得更多的市场份额，相反，在逆向供应链中提高回收价格以获得更多的废旧产品。

4 绩效评价

由结论1和结论2可以得出，在不同决策模式下闭环供应链各节点企业利润不同，具体参见表3，其中A=[Q-(1-a)(c+cr)]2,B=[φ+(1-β)(Δ-cr)]2。。

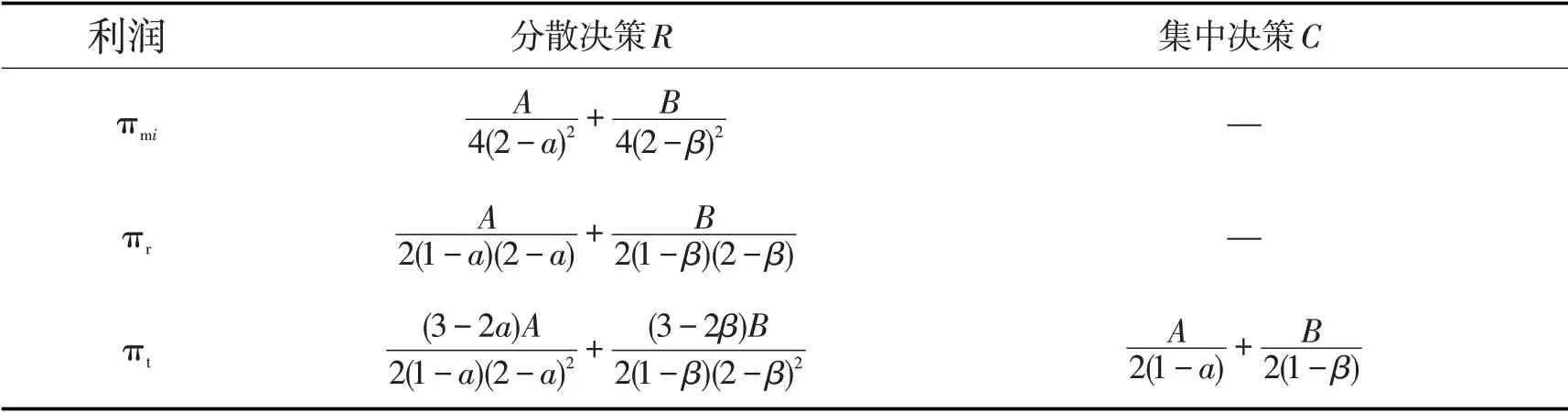
表3 不同决策模式下各企业的利润Tab.3 Each enterprise’s profit under different decisions

5 闭环供应链的协调

由上述结论可以得出闭环供应链在集中决策模式下绩效最高，系统存在优化的可能，通过建立合理的共享契约使得各成员都能够接受，就可以达到系统优化的目的。将系统分为制造商行业M和零售商R两部分。本节基于Shapley值算法对系统进行协调。N={M,R}：闭环供应链的联盟企业。

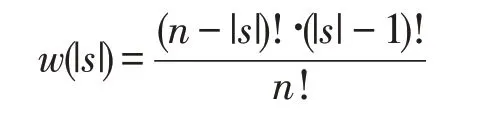
式中：n为联盟企业个数；s为N的子集；v(s)表示s获取的收益；v(si)为子集s去除企业i获取的收益； ||s为子集s中的成员个数；加权因子为w(｜s｜)。协调结果见表4所示。

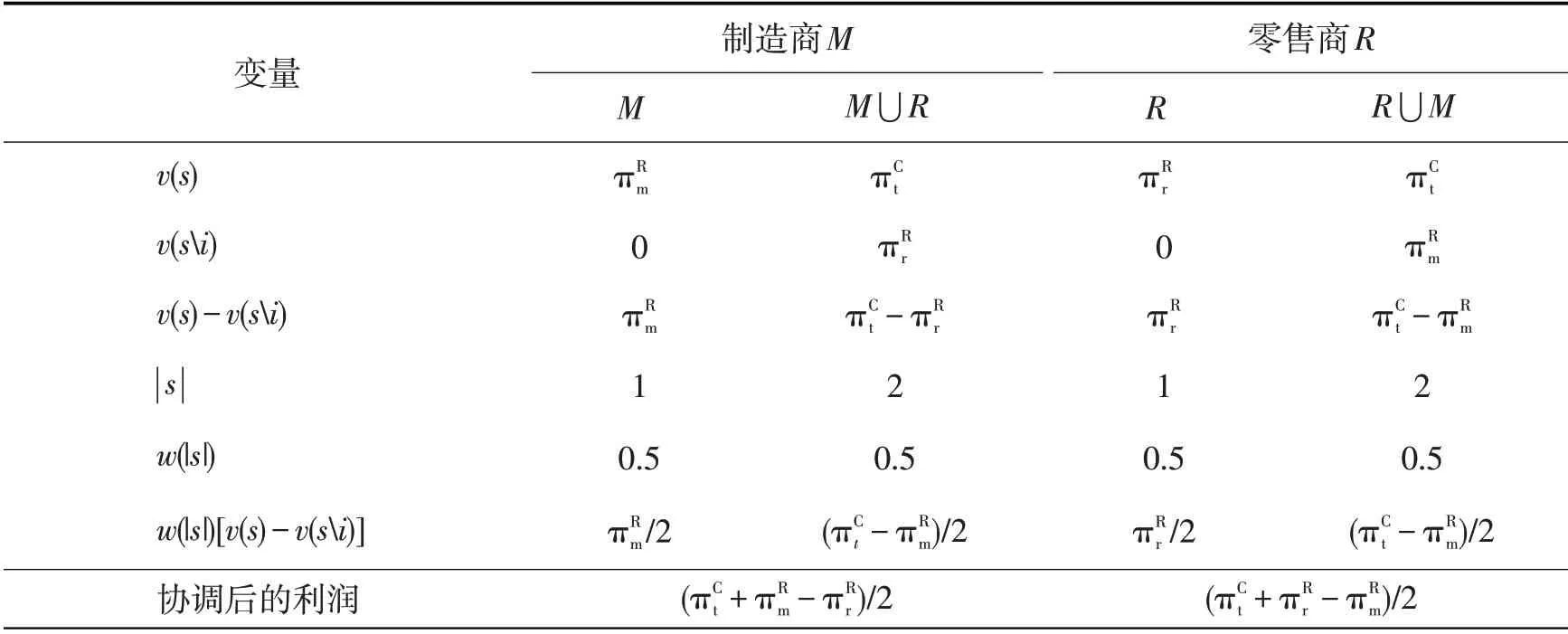
表4 分散决策模型的协调Tab.4 Coordination of decentralized decision model

6 数值分析

下面通过具体的数值对所建模型和结论进行分析。当Q=50，φ=5，α=0.4，β=0.2，c1=c2=c=30，Δ1=Δ2=Δ=25，cr=1［12］时，根据前述2.3节所述模型计算结果如表5。

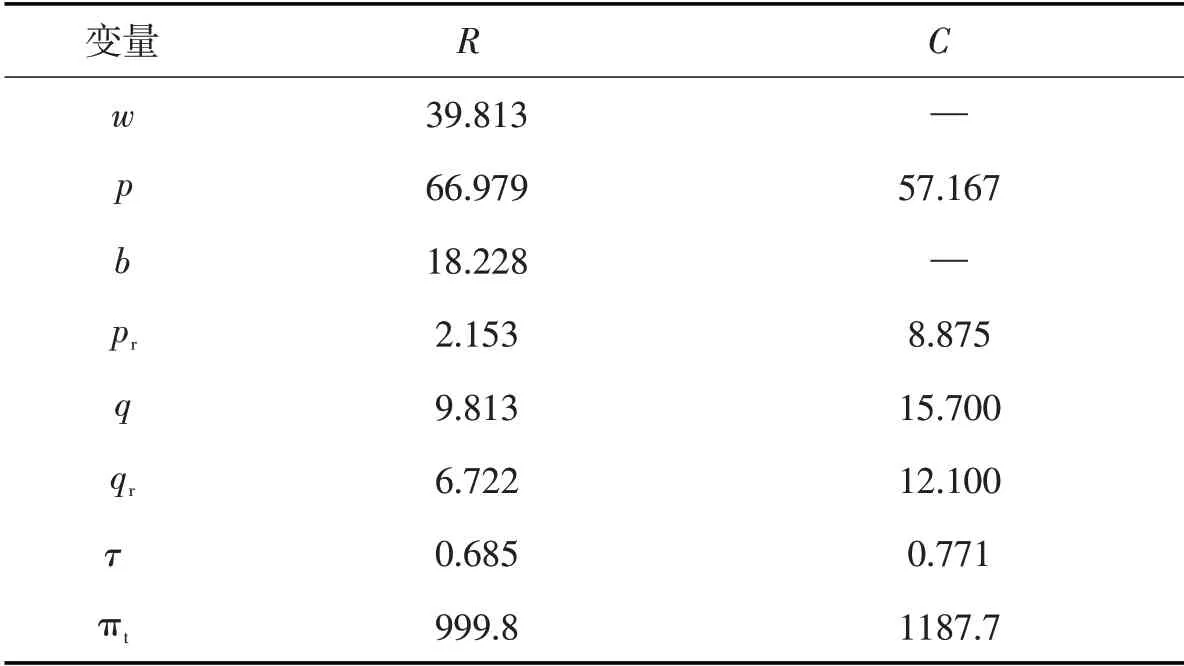
表5 分析结果Tab.5 Analysis results

结论3假设τ为产品的回收率，通过数值分析进一步可得τR＜τC，即集中决策模式下产品的回收率最高。表5表示不同决策模式下各变量数值，验证了上述结论的正确性。

表6 闭环供应链协调前、后利润值Tab.6 Profits of closed-loop supply chain before and after coordination

由表6可以得知，经过Shapley值法协调后的闭环供应链系统及各个节点企业的收益均大于协调前的收益，作为理性的厂商都会接受此协调策略。因此，本研究提出的基于Shapley值法的协调策略是可行的。

制造商领导的竞争闭环供应链在分散决策模式下，制造商和零售商利润随价格敏感系数变化如图2和图3。

图2 价格敏感系数α对利润的影响（β=0.2）Fig.2 Changes of manufacturer’s and retailer’s profit based on sensitive variety α（β=0.2）

图3 价格敏感系数β对利润的影响（α=0.4）Fig.3 Changes of manufacturer’s and retailer’s profit based on sensitive variety β（α=0.4）

基于不同决策模型，系统总利润随价格敏感系数的变化如图4和图5。

图4 系统总利润随α的变化（β=0.2）Fig.4 Changes of the system’s gross profit based on sensitive variety α（β=0.2）

图5 系统总利润随β的变化（α=0.4）Fig.5 Changes of the system’s gross profit based on sensitive variety β（α=0.4）

结论4无论制造商利润、零售商利润还是系统的总利润，均随价格敏感系数α的增加而增加，而且变化幅度较为明显；相反，随价格敏感系数β的增加而减少，变化幅度比较平缓。

7 结束语

从不同决策模式角度出发，针对系统包含两个制造商自由竞争的闭环供应链进行深入分析。通过数学建模和数值分析，研究系统定价与协调，得出如下结论：

1）在信息共享的基础上，当两个制造商的生产成本相同，面对市场环境相同（需求函数以及价格敏感系数等）时，两个制造商自由竞争的结果是相同的产量、转移价格和回收量。

2）在不同的模型中，系统总利润也不相同。C模型中的利润最大，在产品回收率方面，C模型中零售商的回收率最高。

3）利用Shapley值法对制造商领导的闭环供应链模型中的成员进行协调，可以使成员和系统都达到更高的绩效，实现帕累托改进。

只考虑两个制造商之间的自由竞争和单个零售商负责回收两种产品，因此，对于制造商之间的竞争模式和回收渠道的竞争有待于更深入的研究。

[1]GUDIE JR V D,VAN WASSENHOVE L N.The evolution of closed-loop supply chain research[J].Operations Research, 2009,57(1):10-18.

[2]张诚.我国供应链管理研究综述[J].华东交通大学学报,2011,28(3):92-97.

[3]颜荣芳,程永宏,王彩霞.再制造闭环供应链最优差别定价模型[J].中国管理科学,2013,21(1):90-98.

[4]公彦德,李帮义.主导模式对供应链决策、稳定性和效率的影响分析[J].管理工程学报,2012,26(3):42-50.

[5]公彦德.主导模式、回收补贴对闭环供应链决策、稳定性和效率的影响[J].控制与决策,2013,28(8):1263-1270.

[6]CANAN SAVASKAN R,SHANTANU BHATTACHARYA,VAN WASSENHOVE.Closed-loop supply chain model with product remanufacturing[J].Management Science,2004,50(2):239-252.

[7]唐秋生,牛婷婷,马先婷.基于Stackelberg理论的MeRCRM型闭环供应链批量折扣协调机制与定价策略[J].管理工程学报,2012,26(4):183-193.

[8]孙浩,达庆利.基于产品差异的再制造闭环供应链定价与协调研究[J].管理学报,2010,7(5):733-739.

[9]邱若臻,黄小原,葛汝刚.信息共享条件下供应链在线与传统销售渠道协调定价[J].管理工程学报,2009,23(4):74-79.

[10]林欣怡,黄永,达庆利.两周期零售商竞争下的闭环供应链的定价和协调策略研究[J].运筹与管理,2013,22(2):27-34.

[11]王文宾,达庆利.零售商与第三方回收下闭环供应链回收与定价研究[J].管理工程学报,2010,24(2):130-135.

[12]王文宾,达庆利,聂锐.考虑渠道权力结构的闭环供应链定价与协调[J].中国管理科学,2011,19(5):29-37.

[13]赵晓敏,林英晖,苏承明.不同渠道权力结构下的S-M两级闭环供应链绩效分析[J].中国管理科学,2012,20(2):78-87.

[14]郑克俊.存在价格差异的闭环供应链定价策略及契约协调[J].运筹与管理,2012,21(1):118-124.

[15]易余胤.基于再制造的闭环供应链博弈模型[J].系统工程理论与实践,2009,29(8):28-36.

[16]张成堂,杨善林.双渠道回收下闭环供应链的定价与协调策略[J].计算机集成制造系统,2013,19(7):1676-1684.

[17]吴美容,孙浩,赵燕.合作对策的改进Shapley解[J].运筹与管理,2009,18(1):82-85.

[18]李永飞,苏秦,刘强.合作环境及Shapley讨价还价下的供应链质量双边谈判[J].系统管理学报,2014,23(2):159-165.