MMC变流器新型滑模控制器设计

宋平岗，罗善江，杨 姚，文 发，马卫东

（华东交通大学电气与电子工程学院，江西南昌330013）

VSC-HVDC 电压源（voltage source converter，VSC）换流器的高压直流输电（high voltage direct current，HVDC）技术是新一代柔性直流输电技术，而模块化多电平换流器（modular multilevel converter，MMC）以其优越的性能在近几年得到快速发展［1-3］。2013年12月25日，中国南方电网汕头南澳多端柔性之输电工程顺利投产，成为世界首个多端直流输电工程，我国也因此跻身为世界完全掌握多端柔性直流输电成套设备设计、实验、调试和运行全系列核心技术的几个国家之一。基于电压源柔性直流输电系统具有STATCOM功能、无需电网支撑换相、环境影响小等特点，因而在可再生能源发电互联和并网、孤岛和城市供电以及分布式发电等领域具有很强的适用性，在提高电力系统稳定性、改善电能质量等方面具有较强的技术优势［4-6］。

目前MMC的控制器设计广泛采用的是双闭环控制策略，这种双闭环结构建立在基于线性化模型的基础上［7］，在电网扰动以及负载损耗变化情况下稳定性较差［8］，且双闭环PI控制策略需要多个PI控制器，而PI控制器的参数设计目前没有统一规范的方法，因此在实际系统中控制器的调试异常复杂［9］，很难达到理想的效果，动态性能差。为此，针对MMC特有的拓扑结构提出一些先进的控制策略已成为国内外学者的研究热点。滑模变结构控制是20世纪50年代发展起来的一种控制算法，其控制系统在进入滑模运动后对干扰及参数变化具有很强的鲁棒性，且具有自适应性强、动态响应快、稳定范围小等优点［10-11］，特别适合电力电子系统的开关控制。但是滑模控制脉冲信号的产生需直接生成控制开-关动作的开关表，对于MMC多子模块的结构而言，编制开关表的工作过于繁琐和难以理解，失去了滑模控制算法简单、容易实现的优点［12］。

在深入研究MMC 的结构特点和滑模控制理论的基础上，提出一种针对MMC 的新型滑模（new sliding mode，NSM）控制器设计方案。这种将双闭环PI控制和滑模控制相结合的复合控制算法，结合了两者的优点，提高了系统的动态响应和自适应性，同时省去了外环控制器中的PI调节器，大大降低了调试复杂度，具有很强的实际应用价值。

1 MMC基本原理

图1为MMC 拓扑结构图，共有6 个桥臂，为简便起见只画出j（j=a，b，c）相桥臂，每相分为完全相等的上下两个桥臂，每个桥臂由等效电感Ls和N个子模块级联而成，上桥臂用字母“p”表示，下桥臂用字母“n”表示。图中usj和isj为j相交流电压电流，R和L分别为线路等效电阻和漏电感，ucj为MMC交流侧电压，功率参考方向如图所示，ijp和ijn分别表示j相上下桥臂电流，udc和idc分别表示直流侧电压电流。根据基尔霍夫定律，可得MMC运行时的电压方程［13］

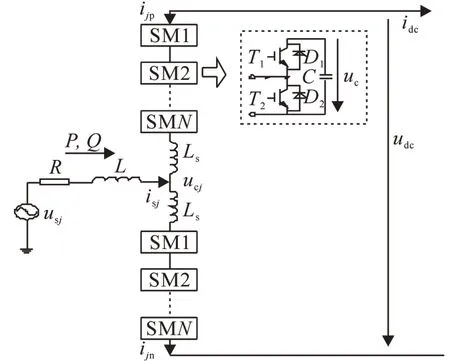
图1 MMC基本拓扑结构Fig.1 Basic topological structure of MMC

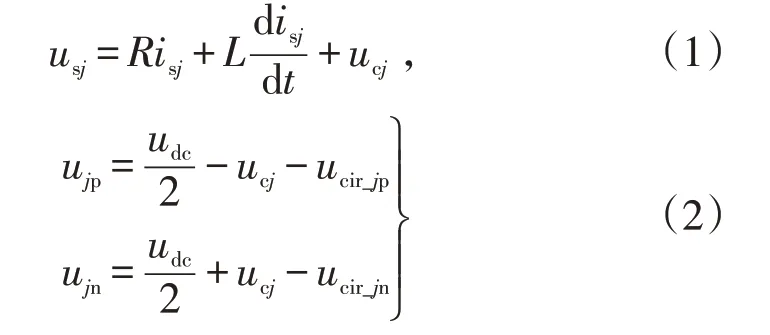
式（1）（2）中ujp和ujn分别为j相上下桥臂投入子模块电压总和；ucir_jp和ucir_jn分别为上桥臂电流和下桥臂电流在各自等效电感Ls上产生的电压。将式（1）所示的3个方程变换至dq坐标系［14］得

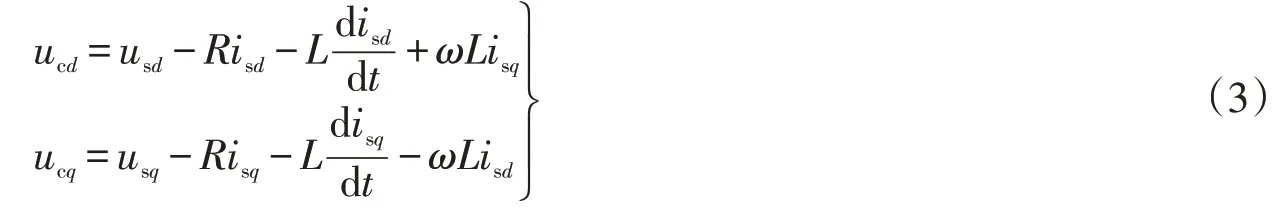
式（3）中下标“d”“q”为abc坐标系变换至同步旋转dq坐标系的相关变量，ucd，ucq分别为换流器输入电压dq分量，usd，usq分别为网侧电压dq分量。一般情况下，虽然MMC每相投入N个额定数目子模块，且时时刻刻都有3C/N大小的等效电容，但是这3N个子模块电容并不是一直都会投入，而是6N个子模块轮流投入［15］，所以直流侧电容等效值为Ceq=6C/N。此时，MMC 可当作是由等效开关函数和直流侧等效电容组成的三相全桥换流器，不考虑换流器损耗和与电感L能量的交换，MMC直流侧动态方程为

式中：sq-eq为MMC等效开关函数；iL为负载线路电流。

2 控制器设计

2.1 电压外环控制器设计

20世纪50年代初，前苏联学者Emelyanov等提出了变结构滑模控制思想，即在相平面法的基础上产生一种现代控制论的综合设计方法。其基本思想是：在控制作用下，使从空间任意点出发的状态轨迹，在规定时间内达到滑模面并在其上做滑动模态运动直至平衡，此后系统运行方式只取决于滑模面方程，与系统原来的参数无关，即系统在一定条件下对外界干扰以及参数扰动不变性从而具有比鲁棒性更加优越的完全自适应性。对于MMC特有的子模块级联结构，可将子模块电容等效至直流侧电容，由上述分析可知Ceq=6C/N，可据此建立滑模控制器模型。

假如η=Udc-ref-Udc，其中Udc-ref为直流侧参考电压，Udc为直流侧电压，当所选取的滑模面［16］为

式中k为滑模控制器系数，通过调节k值大小可使滑模面趋于理想状态。

将（3）（4）带入（5）中可得

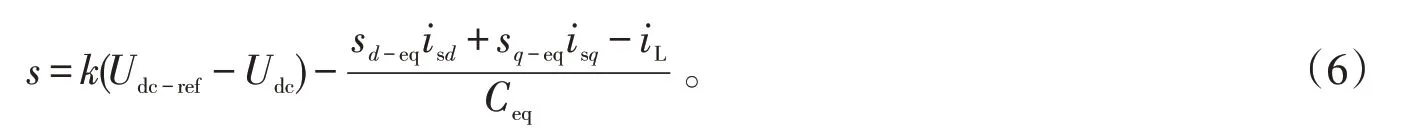
将上式转化在d，q旋转坐标系下表示，可满足如下方程

网侧系统稳态运行时网侧电压三相对称，即Usq=0，isq=0，并且disd/dt=0，disq/dt=0，将其带入式（3）中，可以得到如下方程所示

由上式可得换流器输入电压的计算值，同时将式（7）（8）带入（6）中可以得到

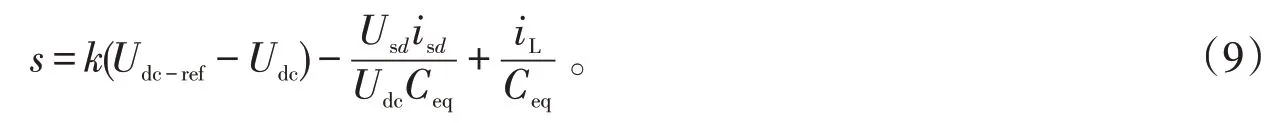
令s=0，得

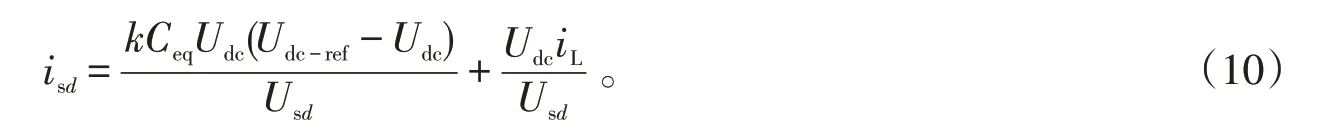
由上式便可以得到内环控制器的参考有功电流i*sd。

2.2 电流闭环控制器设计

将式（3）表示为

其中，vd=Ldisd/dt+Risd，vq=Ldisq/dt+Risq

上式表明，交流侧输出的期望电压不仅与vd，vq（即与isd，isq具有一阶微分关系的电压分量）有关，还与d，q轴电压耦合补偿量ωLisd，ωLisq相关。这是一个非线性系统，应用非线性系统反馈线性化理论设计电流环控制器，从而使非线性系统得以在大范围甚至在全局范围内线性化。其中，vd，vq可采用比例积分实现以补偿在换流电抗器上的电压降，实现方程如式（12）所示，电压耦合补偿量的引入对非线性方程实现解耦控制。

其中：i*sd，i*sq分别为有功和无功电流的参考值。

在本系统中，滑模面为S=i*sd-isd，下面将分析在选择控制率满足广义滑模条件，即SS·＜0。当S＞0时，有i*sd-isd＞0，要满足滑动模到达条件需S·=dS/dt=-disd/dt＜0，稳态时，i*sd=0，即要求选择的控制量增大isd。

由式（11）可得

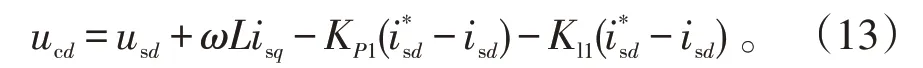
当i*sd-isd＞0时，由式（13）可知，ucd将减小，同理可知，S＜0，有S·成立。

其控制系统框图如图2所示，由图可知，控制系统由一个电压外环和电流内环构成。电压外环稳定输入直流电压，电流环迫使输入电流跟随相电压。对VSR交流侧输入有功功率P和无功功率Q进行分析，可得有功功率和无功功率如下：

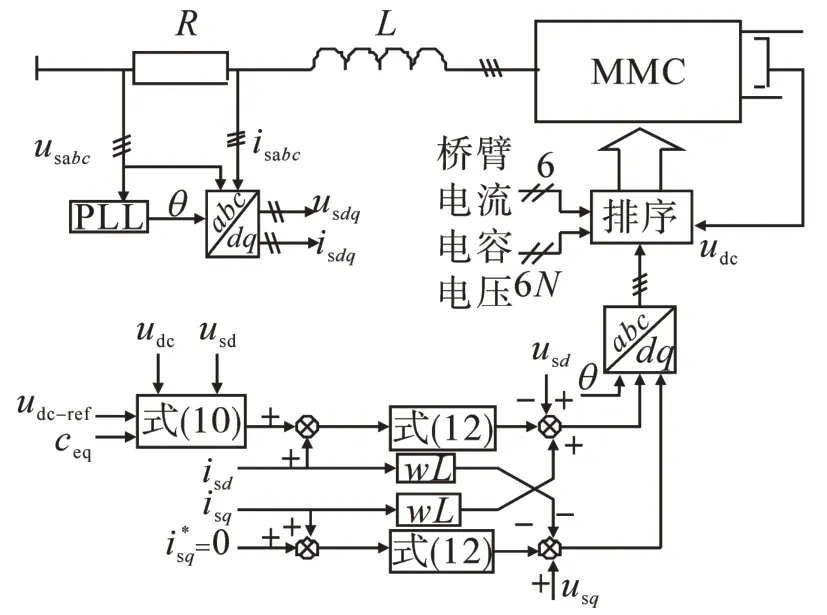
图2 MMC控制系统框图Fig.2 Control system diagram of MMC

由于输入三相电压对称，usd为恒值，因此可以调节无功电流isq来调节无功功率，当MMC整流器运行于单位功率整流状态时，无功功率为0，因此无功功率电流指令为i*sq=0。

3 仿真分析

在MATLAB/Simulink 中搭建上述滑模控制策略以及传统双闭环控制向无源网络供电的MMC-HVDC仿真模型，具体仿真参数如表1所示，整流站和逆变站参数相同，输电线路用几种参数等效。

表1 仿真模型主要参数值Tab.1 Main parameters and values in the simulation model

图3为直流电压波形对比，直流电压参考值设置为20 MV，可以看出，采用新型滑模控制器和双闭环控制器都能使直流电压最终稳定在参考值，但在MMC-HVDC系统中，新型滑模控制器能快速进入稳态且波形较为平滑，具有快速响应性；同时由放大之后的图可以看出，在系统达到稳态后，传统双闭环控制器系统中实际直流线路电压在参考电压周围产生较大波动，而滑模控制器系统波动范围较小，具有较小的误差，因此，新型滑模控制系统具有更高的精确性。

图4为MMC中子模块电容电压波形对比，同样，新型滑模控制器系统能够快速平稳的进入稳态，并且在稳态后与参考值之间的误差较小，如此能有效降低MMC中的环流电流，提高MMC的性能。

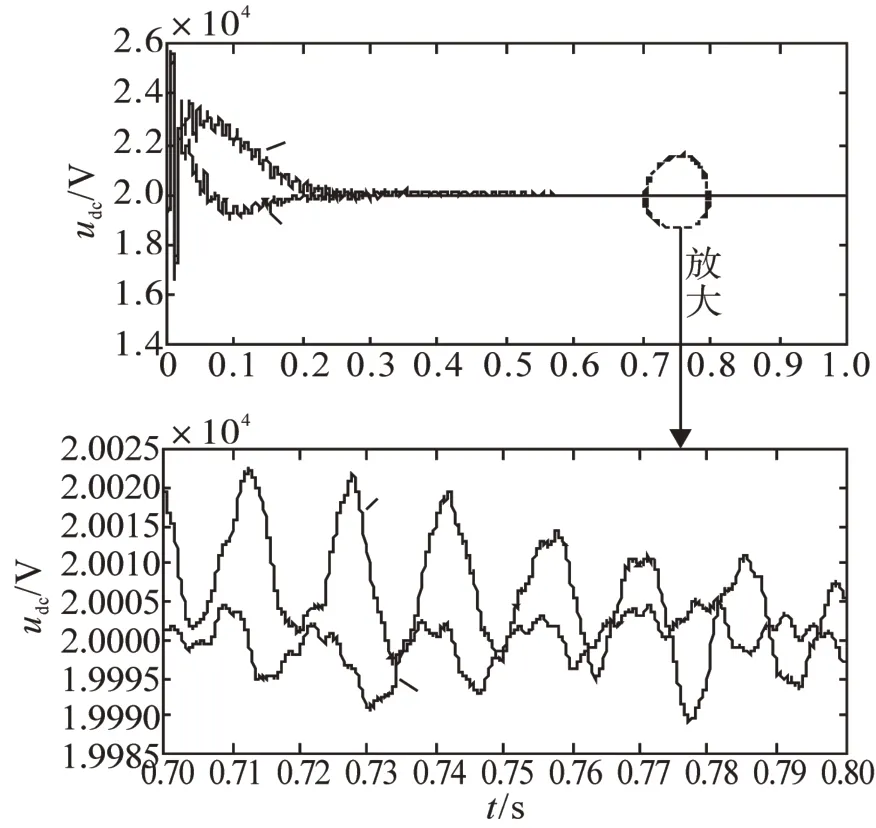
图3 直流电压仿真波形对比Fig.3 Simulation wave comparison of DC voltage

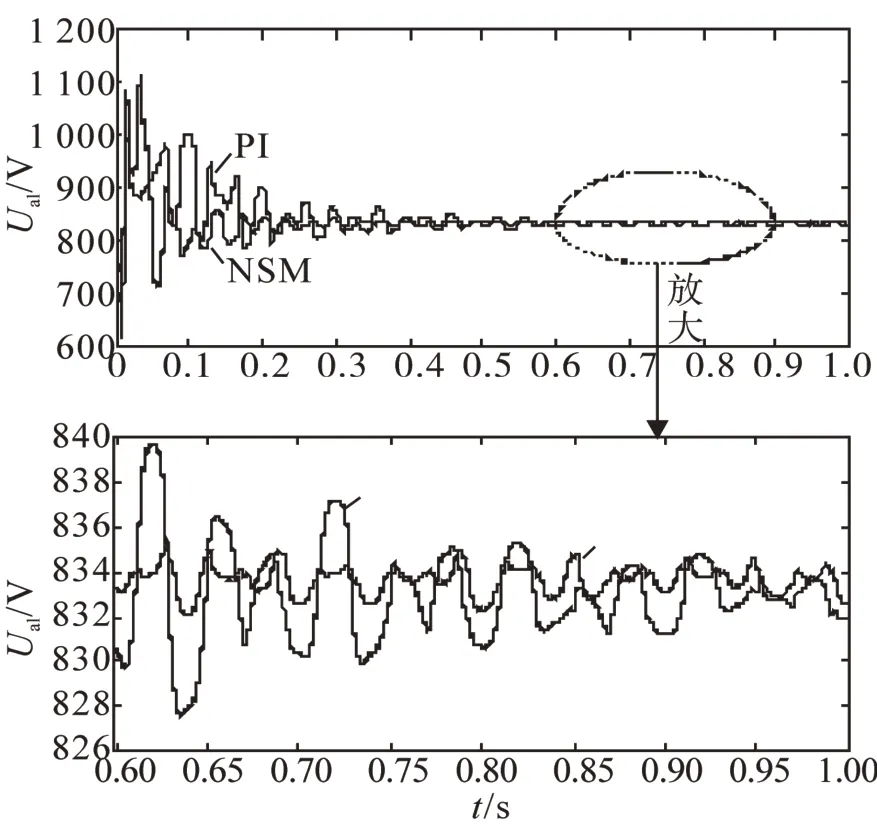
图4 电容电压波形对比Fig.4 Comparison of capacitor voltage

图5为参考电压由20 MV突变至30 MV时直流线路电压对比图，突变时间为1 s处，PI对应波形为传统闭环控制对应的直流电压波形，NSM对应波形为新型滑模控制波形。由图5可知，在参考电压发生改变时，两者虽同时达到稳定状态，但传统闭环控制器在进入稳态过程中直流电压扰动幅度较大，自适应性较差，而新型滑模控制系统则相对较稳定，具有很强的自适应性和抗干扰性。

综合以上几种图例，基于滑模控制理论的新型滑模控制器和传统双闭环控制器相比，前者由于滑模控制理论的应用，使系统的抗干扰性、自适应性以及动态性能等都在一定程度上优于后者，有效改进了现有的控制器。

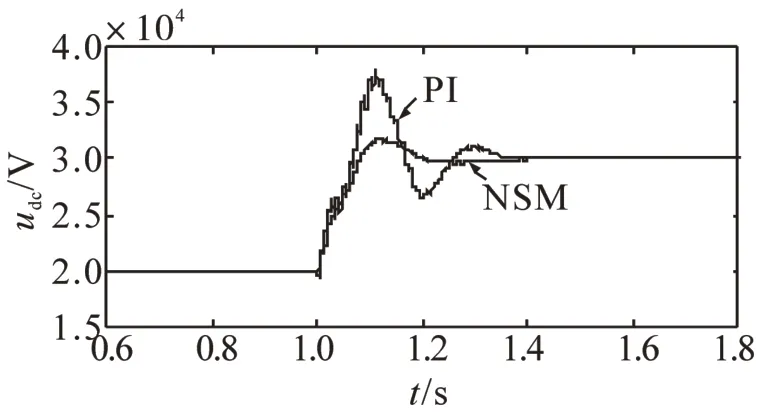
图5 参考电压跳变时直流电压波形对比Fig.5 DC voltage wave comparison of reference voltage step

4 总结

从MMC的数学模型出发，建立了基于滑模控制理论的混合控制器，证明了滑模控制理论在MMC中运用的可行性，并以此为根据设计了一种新型的滑模控制系统，仿真验证该控制系统可提高系统进入稳态的稳定性和平滑度，降低系统误差，在干扰情况下也显示出较强的自适应性和动态性能。

[1] 王珊珊,周孝信,汤广福,等.模块化多电平电压源换流器的数学模[J].中国电机工程学报,2011,31(24):1-8.

[2] 周月宾,江道灼,郭捷,等.模块化多电平换流器型直流输电系统的启停控制[J].电网技术,2012,36(7):204-209.

[3] 徐建中,赵成勇.模块化多电平换流器电容电压优化平衡控制算法[J].电网技术,2012,36(6):256-261.

[4] 孔明,邱雨峰.模块化多电平式柔性直流输电换留器的预充电控制策略[J].电网技术,2011,35(1):67.

[5] ROHNER S, BERNET S, MODULATION.Semiconductor requirements of modular multilevel converter[J].IEEE Transaction on Industry Electronics,2010,57(8):2633-2641.

[6] TU QINGRUI, XU ZHENG, XU LIE.Reduced switching frequency modulation and circulating current suppression for modular multilevel converters[J].IEEE Transactions on Industrial Electronics,2011,262(3):2009-2017.

[7] 王国强,李爽.模块化多电平换流器的直接功率控制仿真研究[J].中国电机工程学报,2013,32(6):64-71.

[8] 陈海荣,徐政.基于同步坐标变换的VSC-HVDC暂态模型及其控制器[J].电工技术学报,2007,22(2):121-126.

[9] HAGIWARA M, AKAGI H.Control and experiment of pulse width-modulated modular multilevel converters[J].IEEE Transactions on Power Elactronics,2009,24(7):1737-1745.

[10] 洪庆祖,谢运祥.基于滑模控制的PWM整流器研究[J].电力电子技术,2012,46(1):34-35.

[11] 马皓,张涛,韩思量.新型逆变器滑模控制研究方案[J].电工技术学报,2005,20(7):13-20.

[12] UTKIN V.Sliding mode in cntrol and optimization[M].Berlin:Springer-Verlag,1992:225-261.

[13] 宋平岗,李云丰,王丽娜,等.一种模块化多电平换流器数学模型的建立方法[J].华东交通大学学报,2013,30(2):37-41.

[14] 陈海荣,张静,屠卿瑞.电网电压不平衡时电压源换流器型直流输电的负序电压补偿控制[J].高电压技术,2011,37(10):2362-2369.

[15] 宋平岗,李云丰,王立娜,等.MMC-HVDC 向无源网络供电的停机策略[J].电网技术,2013,37(11):3247-3253.

[16] 乐江源,谢运祥,洪庆祖,等.Boost变换器精确反馈线性化滑模变结构控制[J].中国电机工程学报,2011,31(30):16-20.

[17] 王恩德,黄声华.三相电压型PWM整流的新型双闭环控制策略[J].中国电机工程学报,2012,25(5):30-37.