一端外伸梁置换法挠度转角方程关系的完备性

喻晓今

（华东交通大学土木建筑学院，江西 南昌330013）

以简单的挠曲线来替代较为复杂者，文献［1］通过分析简支梁、悬臂梁和外伸梁在集中力、集中力偶、分布载荷作用下的最大挠度，发现了简支梁和外伸梁绝对值最大挠度与对应的悬臂梁（置换梁）自由端挠度的同一性，找到了以简代繁的可能性。文献［2］给出了简支梁的比拟梁法（置换法）的转角位移方程和挠度位移方程，适用于简支梁，并以实例应用。文献［3］推导出简支梁和悬臂梁的置换法的转角位移方程和挠度位移方程。文献［4］则以置换法解超静定连续梁，以置换法位移方程直接列写变形协调关系，各型实例说明其良好的适应性。完成导出置换法解一端外伸梁的转角位移方程和挠度位移方程的是文献［5］的工作，这样，置换法求解梁挠度和转角的问题向另一类简单支承梁扩展。在文献［6］中，置换法用于解静定刚架位移。对于铰支承Γ 形刚架的位移，文献［7］作了讨论。Γ 形刚架支承的进一步增加，在文献［8］里提出了解法。文献［9］对一个方向无外力的刚架进行了置换法讨论。而在置换法与它法结合运用上，文献［10］有探讨。为深化置换法的研究，其位移方程本身性质似待揭示。

从梁的挠曲线在其面内的几何图形的观察出发，在任一位置上对挠曲线加入切线作辅助线，并且，一般地作切线的垂线——将该垂线引向梁的有关边界点，此边界点包括支承点和端点等等，构成直线、曲线组成的图形，权且称为置换法图像。对置换法图像进行分析，以平面几何关系和挠曲线所表达的挠度以及其转角为基本变量，建立起它们的等量关系，是置换法寻求位移方程的方法。前研究所找到的位移方程有挠度方程和转角方程，为了进一步落实它们的关系，需要对其性质进行深入研究，以下证明一端外伸梁的挠度方程与转角方程的导数关系。

1 右端外伸梁置换法位移方程之间关系

根据梁的位移的讨论，梁的对称弯曲中，在小变形条件下，梁的挠度与转角是一阶导数的关系，即有w′(x)=θ(x)，其中:w(x)是挠度；θ(x)是转角；x是梁的横截面在变形前的轴向位置坐标。当已经求出挠度方程（挠曲线方程）后，只要对挠度方程求关于自变量x一阶导数，所得函数便是转角方程。置换法所获得的位移方程，包括挠度方程和转角方程皆是关于自变量x的、并存在中间变量的复合函数，就是以置换梁自由端挠度、梁长、跨长、外伸端挠度和x等参数为变量的复合函数，此情况提示应以复合函数的求导法则来验证其包含的挠度方程和转角方程的一阶导数关系。右端外伸梁见图1.

1.1 右端外伸梁置换法图像

作任一右端外伸梁置换法图像见图2，点划线ABC代表梁的变形前轴线位置，其与x 轴重合，点划线ABD为梁轴线变形以后的位置——为明晰而夸大，仍然是浅坦的弹性曲线。x轴原点在梁的左端A处。现于梁的任一位置、离点A为x处的G点处，向下方引一与y轴平行的线段GH，交挠曲线为H点，其即是梁在x位置的挠度（小变形假设）。作H点的切线JK，连接J、A两点，并使线段AJ正交于线JK；同样，连接K、D两点，并使线段DK正交于线JK。显然，线段AJ，DK分别是梁在G处的左、右置换梁自由端的挠度wl(x)，wr(x)（小变形假设）。同理，离梁的A点为x+Δx处的N点处，向下方引一与y轴平行的线段NQ，交挠曲线为Q点，其即是梁在x+Δx位置的挠度。作Q点的切线RS，连接R、A两点，并使线段AR正交于线RS；同样，连接S、D两点，并使线段DS正交于线RS。显然，线段AR，DS分别是梁在N 处的左、右置换梁自由端的挠度wl(x+Δx)，wr(x+Δx)。

另外，切线JK、RS的交点为T；线段AR与切线JK的交点为U；线段DK与切线RS的交点为V。

图1 右端外伸梁Fig.1 Right end overhanging beam

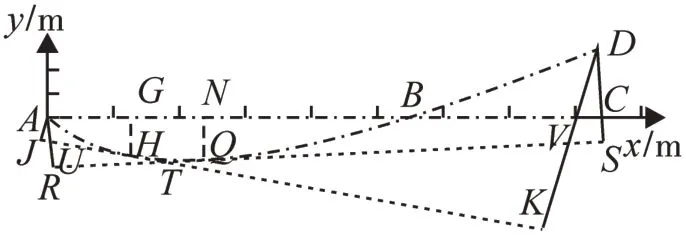
图2 右端外伸梁置换法图像Fig.2 Conversion method graph of right end overhanging beam

1.2 右端外伸梁挠度方程、转角方程

在结构一定、荷载一定的条件下，参考文献［5］给出的右端外伸梁转角方程、挠度方程分别如下

式中：wl(x)表示左置换梁自由端挠度；wr(x)表示右置换梁自由端挠度；l表示跨度；a表示梁外伸部分长度；wC表示外伸端挠度。

式（1）代入式（2）有：

1.3 挠度方程的一阶导数

对式（3）求关于自变量x一阶导数，得

1.4 左右置换梁挠度关系的几何特征

对式（4）中的Ω进行分析。借助于置换法图像，研究的内涵。

研读图2，看直角三角形TUR，TKV，由于∠RTU=∠VTK（对顶角），故它们相似（三角形中两角分别相等）。根据相似三角形的性质，得到等式：

由此可得

因为小变形假设，所有转角都是微小量，并且考虑挠曲线的连续光滑性质，当Δx趋近于零时，也即N点无限地靠近G点时，Q点无限靠近H点，并与T点逐渐合为一点。与此同时，U点趋近于J点；V点趋近于S点。AJ≈AU，DV≈DS（等价无穷小），就是

将式（6）、（7）代入式（5），得：TK(AR-AJ)≈RT(DK-DS)。

再顾及这些线段的物理意义，上式即是

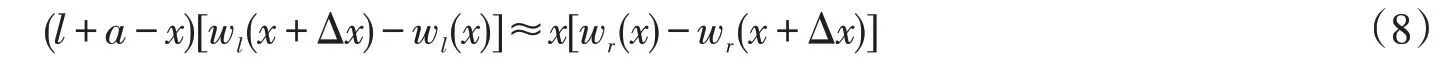
1.5 挠度转角方程的关系

式（8）约等号两边同除以(l+a)Δx因子，得：

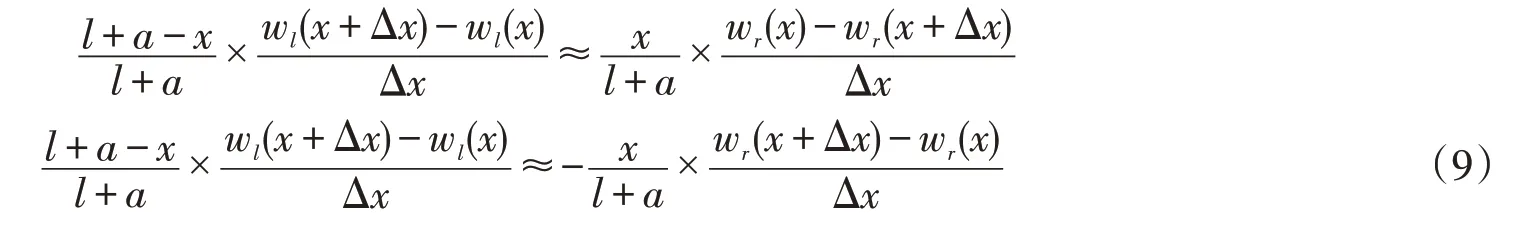
显然，式（9）中约等号两边的各自第二个因子是各自函数增量与自变量的比值，依照导数定义，当Δx趋于零时下式成立：

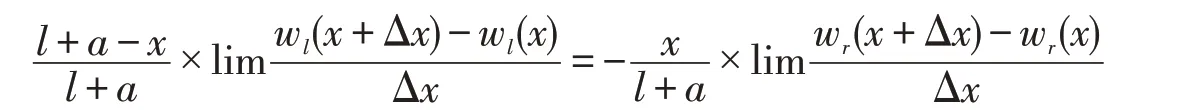
就是：

移项得：

2 左端外伸梁置换法位移方程之间关系

左端外伸梁见图3.以下讨论步骤完全与右端外伸梁的相同，为节省篇幅，采用缩略型语汇，详细逻辑关系参看上述内容。

2.1 左端外伸梁置换法图像

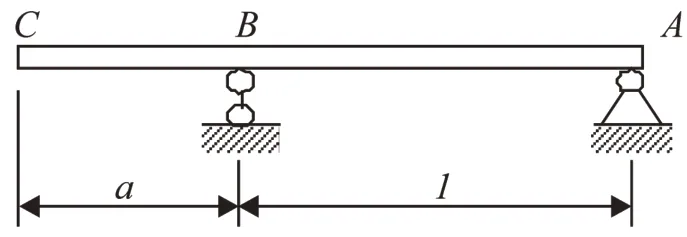
图3 左端外伸梁Fig.3 Left end overhanging beam

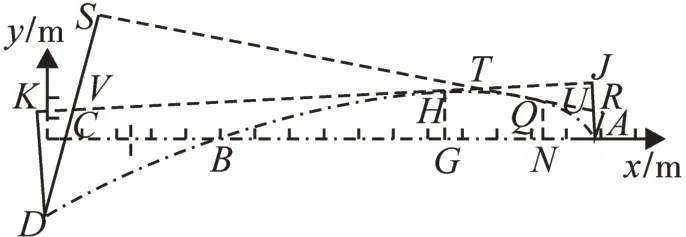
图4 左端外伸梁置换法图像Fig.4 Conversion method graph of right end overhanging beam

作左端外伸梁置换法图像，见图4.不失一般性，点划线ABC代表梁的变形前轴线位置，其与x轴重合，点划线ABD为梁轴线变形以后的位置，仍然是浅坦的弹性曲线。x轴原点在梁的左端C处。现于梁的任一位置、离点C为x处的G点处，向上方引一与y轴平行的线段GH，交挠曲线为H点，其即是梁在x位置的挠度。作H点的切线JK，连接J、A两点，并使线段AJ正交于线JK；同样，连接K、D两点，并使线段DK正交于线JK。显然，线段DK、AJ分别是梁在G处的左、右置换梁自由端的挠度wl(x)，wr(x)。同理，离梁的C点为x+Δx处的N点处，向上方引一与y轴平行的线段NQ，交挠曲线为Q点，其即是梁在x+Δx位置的挠度。作Q点的切线RS，连接R，A两点，并使线段AR正交于线RS；同样，连接S，D两点，并使线段DS正交于线RS。显然，线段DS、AR分别是梁在N处的左、右置换梁自由端的挠度wl(x+Δx)、wr(x+Δx)。

另外，切线JK，RS的交点为T；线段AJ与切线RS的交点为U；线段DS与切线JK的交点为V。

2.2 左端外伸梁挠度方程、转角方程

［5］给出的左端外伸梁转角方程、挠度方程分别如下：

式中符号意义同前。

2.3 挠度方程的一阶导数

将式（10）代入式（11），再对式中变量求关于x一阶导数，得：

2.4 左右置换梁挠度关系的几何特征

对式（12）中的Ω进行分析。研读图4，看直角三角形TUJ，TSV，由于∠JTU=∠VTS，故它们相似。得到等式：

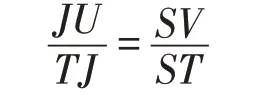
由此可得：

当Δx趋近于零时，也即N点无限地靠近G点时，Q点无限靠近H点，并与T点逐渐合为一点。与此同时，U点趋近于R点；V点趋近于K点。AR≈AU，DV≈DK，就是

将式（14），（15）代入式（13），得：

上式即是：

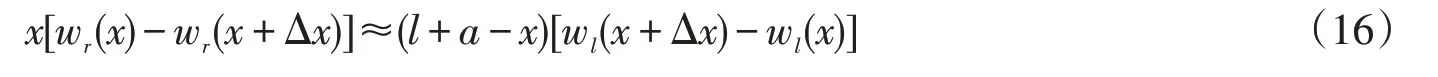
2.5 挠度转角方程的关系

式（16）约等号两边同除以(l+a)Δx因子，得：

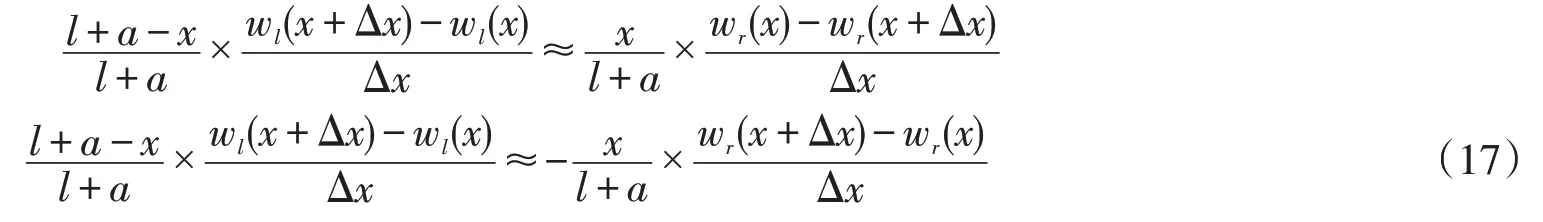
显然，式（17）当Δx趋于零时使下式成立

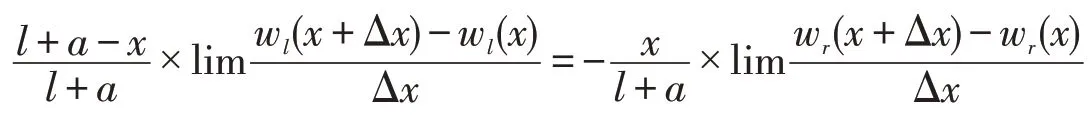
3 结论

置换法位移方程由自变量x、中间变量wl(x)和中间变量wr(x)等等构成，是一组关于x的复合函数。所述复合函数完全适应导数运算的条件和要求。

1）定义的置换梁挠度导数的协和为零。

2）一端外伸梁的置换法挠度方程、转角方程完全符合一阶导数的关系，即w′=θ，故它们也完全保有原梁挠曲线方程和转角方程的关系性质。一端外伸梁的置换法位移方程准确可靠，可以应用于理论分析和工程实践。

参考文献：

[1] 喻晓今.几种荷载下的梁绝对值最大挠度的同一性[J].华东交通大学学报,2000,17(2):40-45.

[2] 喻晓今.以比拟梁法求梁的位移[J].华东交通大学学报,2002,19(4):35-36,40.

[3] 喻晓今.求梁位移的比拟梁法[J].东华理工学院学报,2004,27(4):398-400.

[4] 喻晓今.求超静定等直梁的置换法[J].工程力学,2007,24(S1):66-69.

[5] 喻晓今.一端外伸梁对称弯曲弹性位移的置换法确定[J].力学与实践,2014,36(4):478-482.

[6] 喻晓今.以置换法求静定刚架的位移[J].江西理工大学学报,2007,12.28(6):50-52.

[7] 喻晓今.以置换法求铰支Γ型刚架的位移[J].江西理工大学学报,2008,8.29(4):36-38.

[8] 喻晓今.超静定Г型刚架的置换原理解答[J].华东交通大学学报,2008,12.25(6):1-5.

[9] XIAOJIN YU.Solution of slope of simple frame without force in one direction by principle of conversion method[J].Advanced Materials Research,2012:3141-3144.

[10] XIAOJIN YU.Solution of slope of a frame based on simple support beam coming from method of changing to rigidity by step combined with conversion method[J].Advanced Materials Research,2013:1889-1892.