一维井地电位模型建立与求解
2015-11-22谷建伟李方健李志涛张以根
谷建伟,李方健,刘 洋,李志涛,张以根
(1.中国石油大学石油工程学院,山东青岛266580;2.中石化胜利油田分公司勘探开发研究院,山东东营257015)
一维井地电位模型建立与求解
谷建伟1,李方健1,刘 洋1,李志涛1,张以根2
(1.中国石油大学石油工程学院,山东青岛266580;2.中石化胜利油田分公司勘探开发研究院,山东东营257015)
井地电位法是研究水驱前缘以及剩余油分布较为实用的方法。首先建立一维油水两相渗流方程,基于电位与含水饱和度模型将渗流方程与电位微分方程相耦合,形成一维井地电位模型。对模型采用有限差分法,隐式求压力,显式求饱和度,再利用含水饱和度与电导率的关系,建立形成电位微分方程,隐式求电位;在此基础上建立计算机求解模型。对一维水驱油过程进行模拟计算,通过数值求解,模拟水驱油的完整过程,得到电位分布与含水饱和度变化的相关关系。该方法为井地电位法后期反演油水分布提供理论支持。
井地电位;有限差分法;剩余油;电位方程;方程耦合
井地电位法研究剩余油分布、识别油水通道具有实施容易、对地层无损害、分辨率高、穿透率大、实惠经济等优点。该方法是在地表向井中套管施加一大功率电流,电流通过水泥胶结井段、无水泥胶结井段以及射孔井段非均匀地流向地层(漏电流),从而在非均匀变化的地层中形成非均匀电场,通过测量地表电位分布研究地下介质的电阻率分布[1]。目前国内外学者主要研究了井地电位法在测井方面的应用,还有部分学者以物理模拟形式研究了井地电位在剩余油描述中的应用。章钰[2]针对垂直有限源,利用不完全共轭梯度法进行了三维井地电位正演模拟研究;刘海飞等[3]给出了三维空间任意线源且电导率连续变化的井地电位三维有限元数值模拟方法;Su等[4]进行了井地以及井间联合数值模拟研究的初步探讨;Lines等[5]建立了三维有限差分方程用于解决三维散射问题,但数值模拟结果并未展示;李黎等[6]针对水平管状注水裂隙进行了井地电位异常数值模拟与分析;柯敢攀等[7]利用三维有限元法实现了垂直有限元下三维地下介质电场的正反演研究;Sill等[8]利用井地电位法实现注水前缘推进方向判断;王志刚等[9]进行了井地电位法三维物理模拟实验,直接验证了井地电位法能够有效监测油水通道和剩余油分布。综上所述,很多学者完成了井地电位三维正演模拟研究,且研究方法一致,井地电位模型主要用于测井领域。笔者通过渗流方程与总电位微分方程耦合阐述电位分布与剩余油饱和度的关系。
1 井地电位方程的建立
以一维地层为例,一维测量系统示意图如图1所示。其中A表示供电电极,B表示回流电极。C、D为测量电极用于记录不同位置的地层电位。

图1 一维测量系统示意图Fig.1 Sketch map of one-dimensional measurement system
首先讨论油水两相渗流模型的建立,考虑到源汇项则油层条件下质量守恒形式的数学模型的一般式为

式中,l=o,w分别表示油相和水相;qlv=ql/ρlsc为源汇项,代表地面0℃、0.1 MPa条件下单位体积岩石中注入或采出l相流体的体积流量,m3/s;ρlsc为地面0℃、0.1 MPa条件下l相流体密度,kg/m3;B为流体体积系数;k为油藏多孔介质绝对渗透率,m2;Krl为l相流体相对渗透率,m2;μ为流体黏度,Pa·s;p为流体压力,MPa;ρ为流体密度,kg/m3;g为重力加速度,m/s2;D为标高,由某一基准面算起的垂直方向方向深度(海拔),m;φ为孔隙度;S为流体饱和度;t为时间,s。
根据阿尔奇公式,地层电阻率与储层孔隙度、含水饱和度以及地层水电阻率的关系为

式中,R为地层电阻率,Ω·m;a为比例系数,取值0.6~1.5;m为孔隙度指数,取值1.2~2.0;n′为饱和度指数,这是一个由实验得到的因子,一般取值为2;Rw为充填于孔隙中水的电阻率,Ω·m。
根据电场强度、电位、电流以及电导率的相关关系推导出电位微分方程为

式中,E为电场强度,V/m;U为电位,V;j为电流密度,A/m2;Ω为被包含于曲面τ中的区域;L为一线电流源;I为电流,A;σ为电导率,s/m;Φt为总电位,V。
联立式(2)和式(7),建立含水饱和度与地层电位的相关联系,式(1)与式(7)耦合得到油水两相井地电位数学模型一般式。将三维模型简化至一维并假设:岩石不可压缩;不考虑重力作用的影响;不考虑弹性作用;油水黏度为常数;不考虑毛管力;油水互不相溶均符合达西渗流;供电电极电流均匀,没有奇异性。
建立一维井地电位基本模型为

模型中存在4 个未知量分别为压力、含水饱和度、含油饱和度以及地层电位,因此还需要1个辅助方程:

初始条件为0≤x≤l时,

边界条件为t≥0时,


式(8)~(17)组成了一维油水两相井地电位问题的完整数学模型。通过有限差分法数值求解,数值模拟计算结果中包含每个位置的压力、饱和度、电位等值,可以清晰地看到这些量随时间的变化和分布。
2 差分方程的建立
在油藏渗流领域,有限差分法优点最为突出:实用、方便、简单、准确[8]。本文中选择此法求解。通过隐式求压力、显示求饱和度、隐式求电位3个步骤,按顺序建立差分方程组并进行求解。首先隐式求压力,即将式(8)~(10)进行隐式差分。假设一维网格采用网格间距相同、大小相同的块状网格,并且注水井定义在i=1处的网格,生产井定义在i=n处的网格。
隐式差分结果为

式中,λ为总流动系数。
经过非线性系数线性化显式处理,系数取上游权等中间参数的处理,最终可得三对角矩阵。通过托马斯算法求解矩阵得到每个网格n+1时刻的压力值。然后显示求饱和度,将已求得的n+1时刻的压力值代入式(8)~(10)中得到只含饱和度Swin+1一个未知量的方程,将式(8)~(10)进行两次中心差分,即
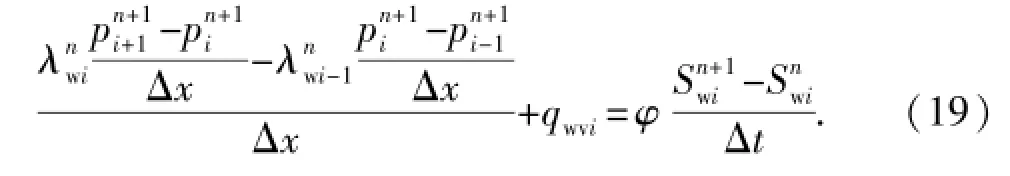
由于每个方程只有一个待求量,因此很容易解得每个网格n+1时刻饱和度的值。

可得矩阵方程为

最后使用编制的计算机程序完成一维井地电位模型的设计与计算。通过模型建立与求解完成地下介质电场正演计算,即已知地层含水饱和度、地层水矿化度、孔隙度等地层电阻率相关参数,求解地表电位数据。现场实际应用井地电位法反演,通过测量地表电位数据反演地下目标层电阻率。实际应用中可利用本文中模型反推,在求得目标层电阻率后,利用阿尔奇公式反演储层处含水饱和度。
3 一维岩心电位计算实例
将岩心视为一维地层,并划分为50个网格,网格步长Δx为2.0 cm;以第一个网格为注水端,最后一个网格为产出端。基础参数:岩心长L为1 m,孔隙度φ为0.3,供电电流I为5 A,初始电位U0取0 mV,水的电导率σw取1250 μs/cm,原油黏度μo为3 mPa·s,地层渗透率k为1 μm2,截面积A为10 cm2,出口端体积流量qt为0.1 cm3/s,时间步长Δt取值2 s,束缚水饱和度Swc为0.2,出口端压力pn为 0.1 MPa,水的黏度μw为1 mPa·s。为了验证方法的正确性,首先计算一维岩心水驱油的压力和含水饱和度分布,结果如图2所示。

图2 不同时刻压力与含水饱和度分布Fig.2 Pressure and water saturation distribution at different moments
从图2可以看出,水驱前缘不断向前推进,每个网格逐渐被水饱和;驱替过程为刚性水驱,模拟计算的压力和含水饱和度特征与理论研究一致,初步验证了模型的正确性。
如图3所示,由于电流源位于注水井处,因此距注水井越远电位越小。从图3还可以看出电导率分布曲线与图2中含水饱和度分布曲线始终同步,推进速度相同,因为含水饱和度与地层电阻率满足式(2),图3中t=200 s和t=800 s时,从电位及电导率对应关系可以看出在水驱前缘位置电位曲线斜率骤变,出现这样差异的原因是水驱到的地方与未驱到的地方含水饱和度差异比较明显,导致地层电阻率、电位在水驱前缘两侧出现较大差异。可以利用这一特性通过监测电位分布识别油水通道,确定注入水在储层中的分布,为评价驱替效果及剩余油分布提供依据。
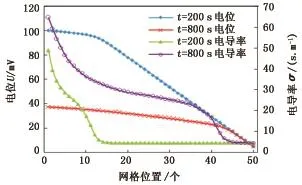
图3 不同时刻网格电导率与电位关系曲线Fig.3 Grid conductivity and potential curve at different moments
前缘突破后电导率与电位关系曲线如图4所示。通过图4可以看出,当注入水突破产出端后,饱和度分布差异导致电导率差异,但差异逐渐减小。实际油田开发过程中,由于地层的非均质性,地层中剩余油分布差异较大,进而引起电导率和电位分布变化,利用电导率即可反求地层中油水分布变化。

图4 前缘突破后电导率与电位关系曲线Fig.4 Conductivity and potential curves after breaking waterfood
实际油田开发过程中要采用三维井地电位模型进行演算。三维井地电位模型在油水饱和度分布及注水优势流动通道描述中的应用还有待研究。该一维井地电位模型主旨在于揭示地下油水分布与电位的密切相关性,可以用于室内岩心驱替过程中油水分布的直接检测。在此基础上推广可以用于指导三维情况下的油水分布解释。
4 结束语
在油水两相渗流模型的基础上,通过阿尔奇公式将渗流方程与电位微分方程相耦合,成功建立了井地电位模型。模型采用有限差分法,隐式求压力,显式求饱和度,再隐式求电位,建立了计算机求解模型并完成一维水驱油过程模拟计算。通过算例验证模型能较准确地将饱和度与电位相联系,并得到两者之间关联关系,利用该关系可以识别油水前缘,分析地层中油水分布特征,为剩余油挖潜、提高采收率和井网优化提供指导。
[1] 王贤君,李建阁,冯立.应用井地电位测量技术判断油层高渗透带方向[J].中国石油大学学报(自然科学版),2006,30(5):68-70. WANG Xianjun,LI Jiange,FENG Li.Orientation determination of high permeability zone with borehole-to-surface potentiometric method[J].Journal of China University of Petroleum(Edition of Natural Science),2006,30(5):68-70.
[2] 章钰.三维井-地电位测井技术正演模拟研究[D].青岛:中国海洋大学,2009:1-15. ZHANG Yu.The forward modeling of three-dimensional borehole-to-surface logging technology[D].Qingdao:O-cean University of China,2009:1-15.
[3] 刘海飞,陈德鹏,戴前伟,等.连续电性介质线源井-地电位三维有限元数值模拟[J].桂林理工大学学报,2011,31(1):29-31. LIU Haifei,CHEN Depeng,DAI Qianwei,et al.3D FEM modeling of borehole-surface potential with line current source in semi-underground space of continuous variation of conductivity[J].Journal of Guilin University of Technology,2011,31(1):29-31.
[4] SU Benyu,YASUHIRO Fujimitsu,XU Jingling.A model study of residual oil distribution jointly using crosswell and borehole-surface electric potential methods[J].Applied Geophysics,2012,9(1):19-26.
[5] LINES L R,JONES F W.The perturbation of alternating geomagnetic fields by three-dimensional island structures[J].Geophys J Roy Astr Soc,1973,32(2):133-154.
[6] 李黎,师学明,张金成,等.水平管状注水裂隙的井-地电位异常数值模拟与分析[J].工程地球物理学报,2011,8(1):73-74. LI Li,SHI Xueming,ZHANG Jincheng,et al.Numeri-cal modeling of well-ground potential anomaly for horizontal tubular crack model[J].Chinese Journal of Engineering Geophysics,2011,8(1):73-74.
[7] 柯敢攀,黄清华.井地电位法的三维正反演研究[J].北京大学学报,2009,45(2):264-266. KE Ganpan,HUANG Qinghua.3D forward and inversion problems of borehole-to-surface electrical method[J]. Acta Scientiarum Naturalium Universitatis Pekinensis,2009,45(2):264-266.
[8] SILL W R,WARDS S H.Electrical energizing of well casings[R].Roosevelt Hot Springs:Univ of Utah Dept of Geol and Geophys,1978.
[9] 王志刚,何展翔,魏文博,等.井地电法三维物理模型试验[J].石油地球物理勘探,2005,40(5):595-597. WANG Zhigang,HE Zhanxiang,WEI Wenbo,et al.3-D physical model experiments of well-to-ground electrical survey[J].Oil Geophysical Prospecting,2005,40(5):595-597.
[10] 李淑霞,谷建伟.油藏数值模基础[M].东营:中国石油大学出版社,2012:134-178.
(编辑 李志芬)
Establishing and solving of a one-dimensional well-ground potential model
GU Jianwei1,LI Fangjian1,LIU Yang1,LI Zhitao1,ZHANG Yigen2
(1.School of Petroleum Engineering in China University of Petroleum,Qingdao 266580,China;2.Institute of Petroleum Exploration and Development,Shengli Oilfield Branch Company,SINOPEC,Dongying 257015,China)
The so-called well-ground potential method is a practical approach to study water flooding front and remaining oil distribution in oil reservoirs.In this paper,based on a one-dimensional equation of oil-water two-phase flow,a relationship between potential and water saturation in coupling with the flow and the electric differentiation equations was established to figure out a one-dimensional well-ground potential model.A finite difference approach was used to solve the model,in which the pressure distribution was computed implicitly,while the fluid saturation distribution was solved explicitly.The potential distribution was calculated implicitly based on the electric differentiation equation.The numerical model can be used to simulate the whole process of water flooding and reveal the variation of potential with the water saturation.The model can provide a useful theoretical basis for the inversion of oil and water distribution from potential field during water-flooding process.
well-ground potential;finite difference method;remaining oil;potential equation;coupled equations
TE 357.7
A
谷建伟,李方健,刘洋,等.一维井地电位模型建立与求解[J].中国石油大学学报(自然科学版),2015,39(6):99-103.
GU Jianwei,LI Fangjian,LIU Yang,et al.Establishing and solving of a one-dimensional well-ground potential model[J]. Journal of China University of Petroleum(Edition of Natural Science),2015,39(6):99-103.
1673-5005(2015)06-0099-05
10.3969/j.issn.1673-5005.2015.06.013
2014-10-30
国家重大油气专项(ZX2011-05009-003);山东省自然科学基金项目(ZR2011EL034)
谷建伟(1971-),男,教授,博士,研究方向为油气田开发。E-mail:gjwLcp@163.com。
