关于阿里巴巴股票价格的实证研究*

薛广明，王 洁，卢若飞

（1.广西财经学院信息与统计学院，广西　南宁　530003；

2.湖南省祁东县第一中学，湖南　衡阳　421600；

3.广西民族大学理学院，广西　南宁　530006）

关于阿里巴巴股票价格的实证研究*

薛广明1，王 洁2，卢若飞3

（1.广西财经学院信息与统计学院，广西南宁530003；

2.湖南省祁东县第一中学，湖南衡阳421600；

3.广西民族大学理学院，广西南宁530006）

基于时间序列分析理论研究基础上，利用SAS统计软件，系统地分析了2010年1月29日至2011年12月16日阿里巴巴港股价格的数据变化规律，拟合滞后变量及时间t模型，从而确定模型并进行预测，最后给出了日、周、月三种不同研究角度下的模型口径及拟合图对比.

阿里巴巴；ARCH模型；残差；自回归；时间序列分析

网络的发展推动了电子商务的进程，目前，“淘宝”“58同城”“赶集”“聚划算”风正在席卷，经济的萧条却带来了网上交易的热潮.

阿里巴巴是全球企业电子商务的著名品牌，汇集海量供求信息，是全球领先的网上交易市场和商人社区，旗下的淘宝网和支付宝，其点击率更是近年的热门.近年来，国内外学者均从文学角度进行了一系列的学术研究，笔者通过SAS统计软件，系统地分析了2010年1月29日至2011年12月16日阿里巴巴港股价格的数据变化规律，拟合滞后变量及时间t模型，从而确定模型并进行预测，最后给出了日、周、月三种不同研究角度下的模型口径及拟合图对比.

1　理论基础

一些时间序列，特别是金融时间序列，在使用ARIMA模型拟合非平稳序列时，对残差序列有一个重要的假定——残差序列｛εt｝均值为零的白噪声序列，换言之，即要满足零均值、纯随机及方差齐性.

若方差齐性假定不成立，即随机误差序列的方差不再是常数，则被称为异方差.

在这三个假定中，零均值通过对序列进行中心化处理就可以实现，纯随机假定，是为了说明残差序列中信息是否提取充分，为了有效检验这个假定，统计学家们构造了许多适用于不同场合的自相关检验统计量，例如Q统计量、LB统计量、DW统计量等.

第三个假定——方差齐性，在金融序列中往往是不满足的，忽视异方差的存在会导致残差被严重低估，从而参数显著性检验容易犯伪纳错误，最终导致模型的拟合精度受影响.

实践中，我们只能根据残差图及残差平方图所显示出来的特点，大致判定残差是否满足方差齐性，而对数变换通常只能使绝大多数金融时间序列的异方差程度得到改善，但无法真正实现方差齐性.

为对异方差函数进行更准确估计，1982年Engle建立条件异方差的模型.

2　模型结构

若ρk恒零时，即异方差函数为纯随机.当存在某个ρk不为零时，说明其自相关性存在，通过构造残差平方序列自回归模型对其拟合即可.

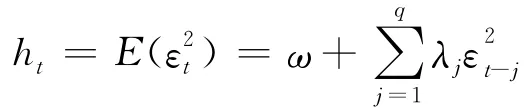
该模型即为ARCH（q），完整结构为：

当残差序列的异方差函数有长期的自相关性，若进行ARCH模型拟合将会有很高移动的平均阶数，同时对参数估计增加难度，且影响ARCH模型拟合度，为改进这一问题，Bollerslov在1985年提出了GARCH（p，q）模型，它的结构如下：

对残差序列｛εt｝拟合GARCH模型时，有时回归函数χt＝f（t，χt－1，χt－2，…）不能充分提取原序列｛εt｝中的相关信息，残差序列可能自相关，而非纯随机.此时需要先对｛εt｝进行自回归拟合，再对自回归残差的序列｛vt｝进行方差齐性检验，若｛vt｝为异方差，则应拟合GARCH模型.这样构造的模型称为AR（m）－GARCH（p，q）模型：

3　实证检验

3.1数据收集及说明

选取2010年1月29日至2011年12月22日阿里巴巴港股（01688）每日收盘价周度数据进行实证研究，数据从搜狐财经网站上获取.其中前99个数据用来建模，后几个数据用来检验模型的拟合程度.

3.2绘制序列时序图

时序图（图1）显示该序列有显著的趋势，为典型的非平稳序列，且看出序列的最大值为17.80，最小值为6.99，均值为13.5531.

图1　2010年1月29日－2011年12月16日阿里巴巴收盘价趋势图Fig.1　On January 29，2010－December 16，2011 Alibaba's closing share price trend chart

3.3残差序列异方差检验

对原序列进行一阶差分，如图2一阶差分后的残差序列具有均值平稳性，而方差是否显著并不明显：观察图3可以从图形上直观地得到结论：残差序列为异方差.

图2　一阶差分图Fig.2　First order difference figure

图3　残差平方图Fig.3　Residual square figure

因为时序图显示序列具有显著线性递减趋势，但波动幅度随时间的变化趋势并不明显，所以笔者尝试｛χt｝关于时间t的线性回归模型及延迟因变量回归两个模型，最终确定一个拟合度较高的模型，并进行预测.

模型1：因变量关于时间t的回归模型

使用AUTOREG过程建立序列｛χt｝关于时间t的线性回归模型，为了从理论上证明残差序列是异方差，我们做了残差序列的Q和LM检验，检验残差序列10阶延迟的自相关性并输出DW检验的P值，同时对残差序列进行异方差检验.

DW检验显示出残差序列具有显著的自相关性，建立残差自回归模型，由残差序列10阶延迟自相关图，显示残差序列至少具有1阶显著自相关性.表1给出了线性回归模型参数估计结果，参数估计结果显示回归模型参数均显著.

表1　线性回归模型参数估计结果Tab.1　Linear regression model parameter estimation results

由Q及LM检验，结果显示残差序列具有显著的异方差性，且具有显著的长期相关性，检验结果如表2所示.

综合考虑残差序列自相关性和异方差性检验结果，尝试拟合GARCH（1，1）模型.模型最终拟合结果如表3所示.

最终模型口径为：

最终输出拟合效果图及95%的置信区间预测图如图4所示：

表2　异方差检验结果Tab.2　Heteroscedasticity testing results

表3　最小二乘估计结果Tab.3　Least squares estimate results

图4　ARCH模型拟合效果图Fig.4　ARCH model fitting renderings

模型2：延迟因变量回归模型

使用AUTOREG过程建立序列｛χt｝关于延迟因变量的回归模型，建立带有延迟因变量的回归模型：χt＝a＋χt－1＋ut.

同模型1，为了从理论上证明残差序列是自相关的，做了残差序列的Dh检验，结果如表4所示：

表4　带延迟因变量回归分析结果Tab.4　With a delay due to variable regression analysis

此处Durbin h统计量的分布函数达到0.1810，这表示残差序列不存在显著的相关性，不需要考虑对残差序列继续拟合自回归模型.

再注意参数检验结果，如表5所示：

表5　参数估计结果Tab.5　Parameter estimation results

在显著性水平默认为0.05的条件下，由表6看出截距项不显著（P值大于0.05），所以考虑在模型拟合命令中增加NOINT选项，最后输出拟合结果如表6、表7所示.

表6　普通二乘估计结果Tab.6　Ordinary least squares estimate results

表7　参数估计结果Tab.7　Parameter estimation results

从模型的拟合程度来说，模型2的拟合度明显高于模型1，因而可以采用模型2进行拟合及预测.

图5　延迟因变量回归拟合效果图Fig.5　Delay dependent variable regression renderings

4　模型预测

用该模型对2011年12月23日至2012年1月27日进行预测，得到的拟合值见表8，然后用搜狐网中已统计的最新真实数据对该模型进行检验，证明其可行性以及预测的可靠性较高.由表8可以看出相对误差在8%以内，证明了模型短期预测的可行性.

表8　2011年12月23日至2012年1月27日预测值与真实值的相对误差Tab.8　On December 22，2011－January 27，2012，The relative error of the predicted values and the real value

5　日、周、月模型及拟合图的比较

笔者对阿里巴巴港股的日数据及月数据也进行了相应的实证研究，得到了日、周、月数据模型建立的对比（如表9所示），并分别给出了它们的拟合效果及95%的置信区间图（如图6～8所示）.

表9　日、周、月度数据模型的比较Tab.9　The comparison of daily，weekly，monthly data model

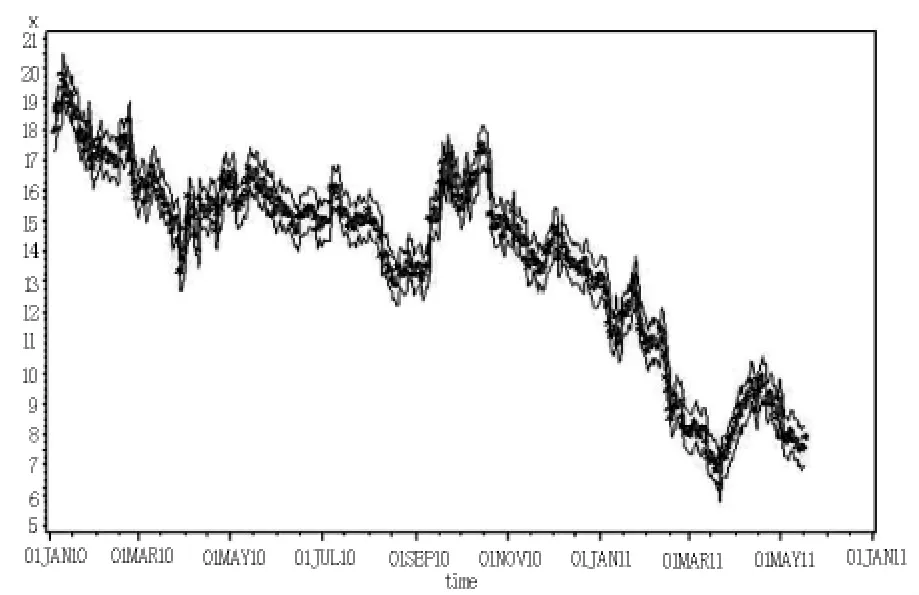
图6　日度数据拟合效果及95%置信区间图Fig.6　Daily data fitting effect and 95%confidence interval

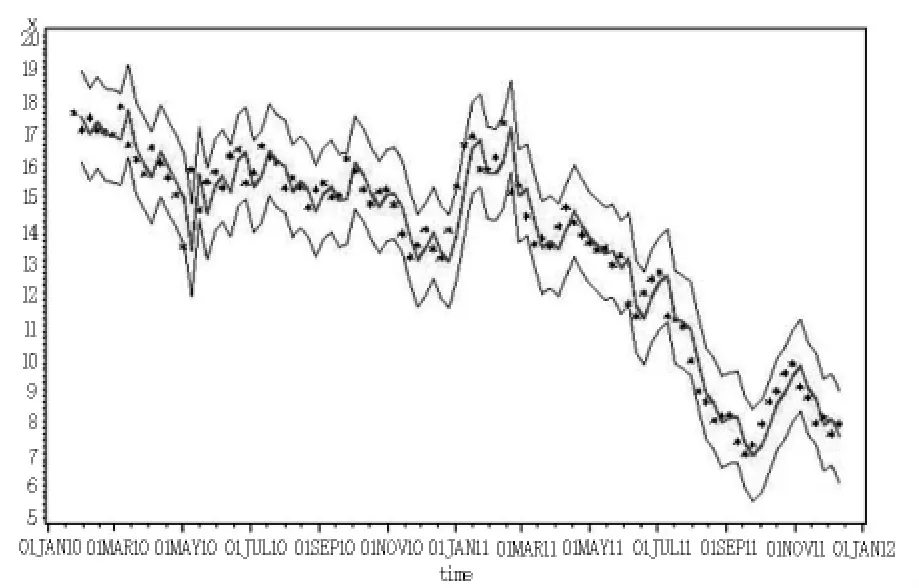
图7　周度数据拟合效果及95%置信区间图Fig.7　Weekly data fitting effect and 95%confidence interval

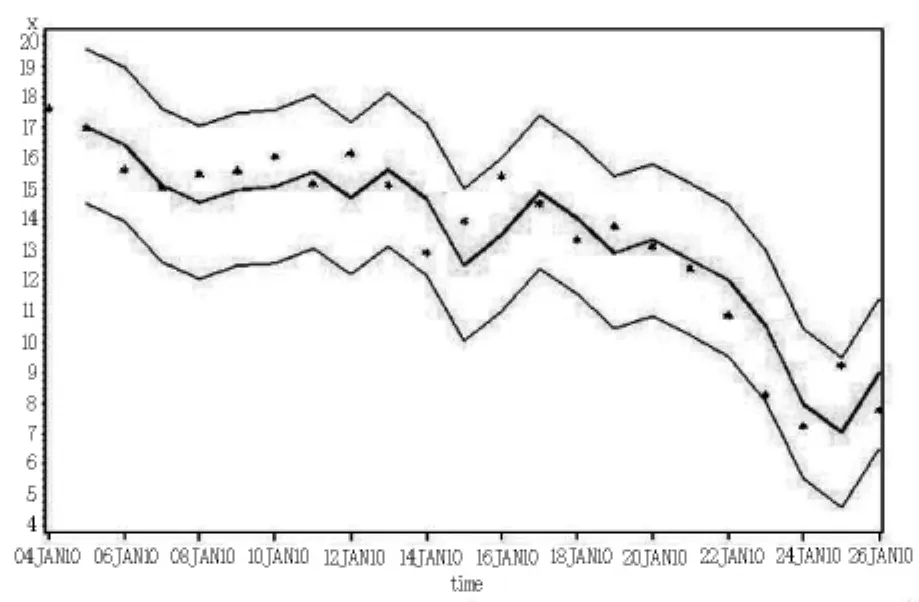
图8　月度数据拟合效果及95%置信区间图Fig.8　Monthly data fitting effect and 95%confidence interval

由日、周、月数据拟合图可以看出，当数据越多时，95%的置信区间相对越小，精度越高，因而人们在股票的买卖过程中，需要全面地分析历年数据，不应单纯地将月度数据或周度数据的研究成果应用于实际中，否则将导致不必要的损失.

6　结语

笔者根据2010年1月29日至2011年12月16日阿里巴巴港股价格的数据变化规律，分别建立｛χt｝关于时间t的线性回归模型及延迟因变量回归两个模型，最终由拟合度确定延迟因变量回归模型，并进行了预测.此外还结合阿里巴巴港股的日收盘数据与月收盘数据，可以给投资者一定的启示，观察数据量的多少能给投资者带来不一样的判断角度，从而避免片面地观察数据，减少投资中不必要的人为损失.

[1]王燕.应用时间序列分析[M].北京：中国人民大学出版社，2010.

[2]高惠璇，耿直，等.SAS系统·SAS/ETS软件使用手册[M].北京：中国统计出版社，1998：66－78.

[3]邓祖新.数据分析方法和SAS系统[M].上海：上海财经大学出版社，2006：411－423.

[4]谢佳利，杨善朝，梁鑫.我国CPI时间序列预测模型的比较及实证检验[J].统计与决策，2008（9）.

[5]杜普燕，宋向东，任文军.ARCH模型在金融时间序列中的拟合应用[J].佳木斯大学学报：自然科学版，2009（2）.

[6]梁鑫，庞丽，彭冬梅.桂林市汽车销售量的时间序列预测模型[J].广西科学，2008（4）.

[7]梁鑫，谢佳利，李朝.广西GDP的统计预测模型及其应用[J].经济数学，2008（3）.

[责任编辑 苏 琴]

[责任校对 方丽菁]

An Empirical Study of Alibaba Stock Prices

XUE Guang-ming1，WANG Jie2，LU Ruo-fei3
（1.School of Information and Statistics，Guangχi University of Finance and Economics，Nanning530003，China；2.Hunan Province Qidong County First Middle School，Hengyang 421600，China；3.College of Science，Guangχi University for Nationalities，Nanning530006，China）

This article is based on time series analysis theory，by statistical software，systematically analyzed on January 29，2010－December 16，2011stock price data alibaba change rule，fitting lag variables and time t model to determine the model prediction，and finally gives the day，week，month three different research Angle of the model diameters and fitting contrast diagram.

alibaba；The ARCH model；Residual；autoregression；Time series analysis

F224

A

1673－8462（2015）01－0051－05

2014-09-20.

国家自然科学基金（11461008）；教育部人文社科基金（13YJA910003）；广西自然科学基金（2013GXNSFAA019005）；广西高等学校科学技术研究重点项目（2013ZD010）.

薛广明（1985-），男，黑龙江齐齐哈尔人，硕士，广西财经学院助教，研究方向：随机分析、计量经济与金融工程.