交流杂散电流对管道交流干扰电压的影响

鲍元飞,李自力,许 甜,王吉青

(1. 中国石油天然气管道局，廊坊 065000； 2. 中国石油大学(华东)，青岛 266580；3. 中国石油工程建设公司 华东设计分公司，青岛 266071)



交流杂散电流对管道交流干扰电压的影响

鲍元飞1,李自力2,许 甜3,王吉青3

(1. 中国石油天然气管道局，廊坊 065000； 2. 中国石油大学(华东)，青岛 266580；3. 中国石油工程建设公司 华东设计分公司，青岛 266071)

根据目前在油气管道运行过程中日益增加的交流电气化铁路与埋地管道平行或交叉等情况，通过实验室管道试验，研究了管轨并行间距、并行长度以及交叉角度对交流干扰电压的影响规律。结果表明，交流杂散电流干扰下管道交流干扰电压随并行间距和长度呈现逻辑函数变化，并随交叉角度的增大而减小。所得规律可以对管道运行过程中杂散电流的排流进行理论指导。

交流杂散电流；管道交流干扰电压；并行间距与长度；交叉角度

随着电气化铁路与电力工业的发展，在受地形限制的“公共走廊”内，管道与电气化铁路呈现平行或者交叉状态，管道受到杂散电流干扰腐蚀的危险性增加[1]。目前，控制管道腐蚀的有效措施是管道外敷设防腐层，同时对管道进行外加阴极电保护[2]。但是由于防腐蚀层针孔缺陷的存在，以及施工中不可避免的对防腐蚀层划伤和刺伤的破坏，使管道与外界电解质环境接触[3]。在交流杂散电流的干扰下，涂层缺陷处形成局部腐蚀，致使管道穿孔[4]。管道交流干扰电压是交流杂散电流干扰下的管道对地交流电压，亦称为交流管地电位，作为管道受杂散电流干扰强弱的一项评价标准，在管道干扰腐蚀预测和排流保护方面有重要作用[5]。目前，对管道交流干扰电压主要通过试片试验研究，管道试验的研究相对较少，本工作通过对Q235钢质管道电位的研究，得到不同因素对管道交流干扰电压变化的影响，对管道杂散电流排流具有很好的参考意义。

1 试验

1.1 试验装置

试验采用管径为φ20 mm×2.5 mm×3.0 m、材质为Q235的钢管，在室内隔离箱体内的埋深为0.5 m。钢管外壁用防潮、防漏电、防腐蚀的绝缘漆粉刷，绝缘漆表干后用防水绝缘胶带紧密缠绕。在管道两端及0.8 m,1.5 m,2.2 m处共取五个测点。试验中的杂散电流干扰源为恒电流输出，并通过回流极和泄流极向埋地管道施加杂散电流，试验中泄流极与回流极的连线(模拟电气化铁路泄流点和回流点之间轨道长度)与埋地管道呈现平行或者交叉关系。埋地管道的交流干扰电压通过数据采集卡采集，试验装置如图1所示。

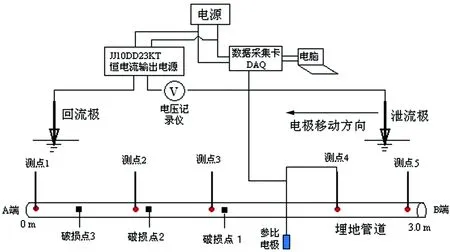
图1 埋地管道交流管地电位测量试验装置示意图Fig. 1 The schematic diagram of pipe-soil AC voltage experimental set-up

1.2 试验内容

交流电气化铁路杂散电流影响埋地管道交流干扰电压的因素主要有：管轨并行长度L、管轨并行间距D、管轨交叉角度α、杂散电流强度I等。因此试验通过管轨并行试验和交叉试验，分析了上述几个因素的干扰影响。

(1) 并行试验 分析并行长度和间距这两种因素对埋地管道防腐蚀层产生的影响。由于不同的防腐蚀层缺陷位置可能对电流的流入流出产生影响，因此设计了两种不同的防腐蚀层破损状况进行对比，如图1中所示的破损点1～3，分别位于0.5 m、0.85 m、1.6 m处，破损面积均为1 cm2。试验时，并行长度L变化范围为0.5～3.0 m，并行间距变化范围是0.15～0.9 m。

(2) 交叉试验 分析不同管轨交叉角度对交流管地电位的影响。设定管轨交叉角度α分别为10°、20°、30°、45°、60°、75°、90°。试验时，固定回流极位置不变，泄流极从管道上方逐渐靠近回流极，记录交流管地电位随电极间距l的变化。

(3) 杂散电流干扰强度试验 分析不同杂散电流强度对交流管地电位的影响。杂散电流强度变化范围为0.1～0.7 A，在防腐蚀层破损点1、2存在时，试验对杂散电流干扰点靠近和远离防腐蚀层破损点的情况作了对比试验。

2 结果与讨论

2.1 管轨并行试验分析

破损点1和2同时存在，杂散电流干扰强度为0.1 A时，采集在不同管轨并行长度下的交流管地电位随并行间距的变化值，得到如下表1所示数据。

表1 破损点1和2条件下不同并行间距下的交流管地电位值

破损点2和3同时存在，其他条件不变，得到如表2所示交流管地电位随并行间距的变化值。

表2 破损点2和3条件下不同并行间距下的交流管地电位值

通过上述表中数据，从并行长度和并行间距两个影响因素出发，分析交流管地电位的变化规律，具体分析如下。

(1) 并行间距分析 将上述表1、2中的并行间距作为自变量，分析交流管地电位随并行间距的变化规律。对各并行间距下的点均采用logistic函数进行曲线拟合，拟合方程如下式(1)所示。

(1)

通过logistic函数曲线拟合，得到如下图2所示交流管地电位变化曲线。

(a) 破损点1、2存在时的电位变化曲线

(b) 破损点2、3存在时的电位变化曲线图2 交流管地电位随并行间距的变化曲线Fig. 2 The relation curves between the pipe-soil AC voltage and parallel spacing(a) pipe-soil AC voltage curves in the presence of defects 1 and 2(b) pipe-soil AC voltage curves in the presence of defects 2 and 3

经分析，图2(a)中曲线的拟合相关系数R2值均大于0.99，非常接近1；图2(b)中曲线的R2值略小，但是同样非常接近1，拟合结果较好，因此logistic函数可以很好地描述试验规律。由图2中曲线可以看出，随着并行间距的增大，交流管地电位逐渐减小；由于防腐蚀层破损点位置不同，图2(b)中曲线变化相对平缓。为了进一步分析电位变化规律，对图中每条曲线求导数，得到导数曲线如图3所示。

(a) 破损点1、2存在时的导数曲线

(b) 破损点2、3存在时的导数曲线图3 交流管地电位随并行间距变化的导数曲线Fig. 3 The derivative curves between the pipe-soil AC potential and parallel spacing(a) the derivative curves in the presence of defects 1 and 2(b) the derivative curves in the presence of defects 2 and 3

图3(a)中并行间距为0.3 m左右处的各个导数曲线的导数绝对值最大，即交流管地电位变化速率最大。图3(b)中并行间距为0.4 m左右处的导数绝对值最大，但是要小于图3(a)中导数绝对值的最大值。总体看来，图3(a)中导数绝对值要大于图3(b)中的值。这说明破损点越靠近管轨并行段，交流管地电位的变化越剧烈；当破损点远离管轨并行段时，交流管地电位的变化趋于平缓。因此要提高管轨平行段管道的防腐蚀层质量。

同时可以看出，在管轨间距大于0.4 m左右之后，导数曲线的导数绝对值逐渐减小。当管轨间距大于0.70 m之后，曲线变化速率已经非常小，管轨间距对交流管地电位的影响也已经很小。

(2) 并行长度分析 将上表1、2中的并行长度作为自变量，分析交流管地电位随并行长度的变化规律，得到图4所示的曲线。

对图中不同并行长度下的各个点同样采用logistic函数进行拟合，拟合方程同样为上式(1)。经分析，图4中每条拟合曲线的相关系数R2均大于0.99，拟合效果很好。因此，logistic函数同样可以描述交流管地电位随并行长度的变化规律。从图4可以看出，随着并行长度的增大，交流管地电位一开始迅速增大，然后缓慢增加并趋于平缓，关系曲线基本呈现“S”形变化趋势。由于破损点位置的不同，曲线的具体形状有所差异，但是体现的规律性是一致的。

(a) 破损点1、2存在时的电位变化曲线

(b) 破损点2、3存在时的电位变化曲线图4 不同并行间距下交流管地电位随并行长度的变化曲线Fig. 4 The relation curves between the pipe-soil AC voltage and parallel length(a) pipe-soil AC voltage curves in the presence of defects 1 and 2(b) pipe-soil AC voltage curves in the presence of defects 2 and 3

为了进一步分析交流管地电位随并行长度的变化规律，将由图4中的曲线求导数，并得到如图5所示的导数曲线。

通过图5的导数曲线也可以看出，交流管地电位与并行长度之间的关系呈现“S”形变化趋势。图5(a)中导数曲线在并行长度为0.9 m处的导数值最大，(b)中导数曲线在并行长度为1.2 m处的导数值最大，说明此并行长度下的交流管地电位变化速率最大。此点之后，随着并行长度的增加，导数值逐渐变小。当并行长度为2.3 m左右时，导数值已经非常小，并行长度这一因素对交流管地电位的影响也很小。

2.2 管轨交叉试验分析

在不同的管轨交叉角度下，测量交流管地电位随两电流极之间距离l的变化，如表3所示。

对不同管轨交叉角度下的点均采用allometric函数进行曲线拟合，拟合方程如式(2)所示。

(2)

通过allometric拟合，将上表中的交流管地电位随两电极间距l的变化绘制曲线，如图6所示。

(a) 破损点1、2存在时的导数曲线

(b) 破损点2、3存在时的导数曲线图5 交流管地电位随并行间距变化的导数曲线Fig. 5 The derivative curves between the pipe-soil AC potential and parallel length(a) the derivative curves in the presence of defects 1 and 2(b) the derivative curves in the presence of defects 2 and 3

经分析，图中各点allometric曲线拟合的相关系数R2值基本大于0.99，非常接近1，拟合结果较好，因此在试验管段范围内，allometric函数可以很好地描述试验规律。

由上图可以看出，随着管轨交叉角度从10°变化到90° ，曲线依次从上到下排列，也即在相同的电流极之间距离的条件下，管轨交叉角度越大，交流管地电位越低。同时可以看出，交叉角度小于60°时，曲线陡峭，斜率较大；交叉角大于60°时，曲线平缓，且曲线相互间靠的很近。因此管轨交叉时，尽量使管轨垂直以减小杂散电流的影响，在客观条件不满足的情况下，要保证管轨交叉角度大于60°。由上图同样可知，在同一交叉角度下，随着两电流极极之间的距离增大，交流管地电位也逐渐增大。这是因为两电流极之间距离越大，电极之间的回流电阻越大，通过管道的杂散电流数量越大，交流管地电位值也就越大。

表3 不同交叉角度下交流管地电位的变化值

图6 不同交叉角度下的交流管地电位变化曲线Fig. 6 The pipe-soil AC voltage curves at different crossing angles

2.3 交流干扰强度试验分析

试验分为两组，对远离和靠近防腐蚀层破损点的两种情况进行了对比分析，具体试验数据如表4所示。

将上表中交流管地电位随杂散电流干扰强度的变化，采用linear线性拟合，拟合方程如式(3)所示。

(3)

通过linear线性拟合得到如图7所示拟合曲线。

通过分析，靠近防腐蚀层破损点的linear曲线拟合的相关系数R2值均大于0.999，非常接近1，拟合结果很好；远离防腐层破损点的linear曲线拟合相关系数较小，基本大于0.9，拟合度较低。可见，越靠近防腐蚀层破损点，杂散电流强度对交流管地电位的影响越呈现出线性的变化规律，而远离破损点时的线性较弱，经分析，远离破损点时可以用ExpDec1函数较好的拟合。

表4 不同情况下的交流管地电位随交流干扰强度变化值

图7 不同杂散电流干扰强度对交流管地电位的影响Fig. 7 The influence of different stray current intensity on pipe-soil AC voltage

由图7可知，管轨间距越小，曲线的斜率越大，相同的干扰强度下交流管地电位越大。图中靠近防腐蚀层破损点直线中，管轨间距为0.30 m的直线斜率很大，而间距为0.75 m和0.90 m的直线斜率相差不大，且基本重合。说明管轨间距在小于定值范围内对交流管地电位影响大，超过一定值时，影响很小。这一定值在上图中约为0.75 m左右，与管轨并行间距试验中的0.70 m基本相一致。

由图7同样可知，距离防腐蚀层破损点越近，交流管地电位越大；反之，交流管地电位越小，如图所示的远离防腐蚀层破损点的三条直线基本重合，且斜率很小。因此在远离防腐蚀层破损点时，并行间距的影响变小，这一点可以与并行间距试验中破损点2、3存在时的规律相对应。

3 结论

管轨并行间距和并行长度这两个因素的影响均可以用logistic函数描述，而管轨交叉角度这一因素的影响可以用allometric函数描述。最后通过对杂散电流干扰强度的分析，印证了前面得到的规律性。由于在独立试验箱中的试验屏蔽了其他干扰因素的影响，因此得到的结论具有较好的可靠性，对于管道杂散电流排流可以提供参考。

[1] AL-BADI A H. Safe separation distance between 132 kV power lines and nearby metallic conductors[J]. International Conference on Communication,Computer & Power(ICCCP′07)，2007，2：19-21.

[2] 孙秋霞. 材料腐蚀与防护[M]. 北京：冶金工业出版社，2004：92.

[3] 曹楚南. 腐蚀电化学原理[M]. 北京：化学工业出版社，2008.

[4] 郝宏娜，李自力，衣华磊,等. 能源公共走廊内管道交流干扰腐蚀判断准则[J]. 油气储运，2012，31(4):16-18.

[5] 赵晋云，滕延平，刘玲莉,等. 新大线管道杂散电流干扰的分析与防护[J]. 管道技术与设备，2007，2:41-43.

Influence of AC Stray Current on AC Interference Voltage of Pipeline

BAO Yuan-fei1, LI Zi-li2, XU Tian3, WANG Ji-qing3

(1. China Petroleum Pipeline Bureau, Langfang 065000, China； 2. China University of Petroleum (East China), Qingdao 266580, China; 3. Huadong Design Branch, China Petroleum Engineer & Construction Corporation, Qingdao 266071, China)

According to the increasing parallel or crossing conditions between AC electrified railway and buried pipeline system during pipeline operation, the influence of parallel spacing, parallel length and cross angles on the AC disturbance voltage was researched by laboratory pipeline experiments. The results showed that under the influence of AC stray current, there existed logic function relationship between the AC disturbance voltage of pipeline and the parallel spacing and length, and the AC disturbance voltage decreased with the increase of cross angle. The drawn conclusions can provide theoretical guidance for the drainage of AC stray current duing pipeline operation.

AC stray current； pipe to soil AC influence voltage； parallel spacing and length； crossing angle

2014-06-03

中国石油天然气股份有限公司西部管道分公司：750 kV交流输电线路和电气化铁路对埋地管道阴保系统的干扰评价及防控技术研究

李自力(1963-)，博士生导师，从事油田腐蚀与防护、油气计量技术等方面研究，15053293355,lizili@upc.edu.cn

TG174

A

1005-748X(2015)03-0221-05