一类极小系统的动力性状

颜棋，尹建东

（南昌大学 理学院，江西 南昌330031）

（X，f）为一个紧致系统，X为紧致度量空间，f为X上的连续自映射.要研究（X，f）的动力性状，一种常见的用法是研究该系统的全部子系统，即系统的全部不变子集，并弄清楚各子系统的性质及原系统之间的关系.从而那些不可再分解的更小的系统成为研究的主要对象.拓扑动力系统的核心问题是研究点的轨道渐近性或拓扑结构.为了能够更深刻地刻画拓扑动力系统中点的轨道结构与遍历内涵，相继引进了弱几乎周期点和拟弱几乎周期点这两个概念［1－2］，并指出存在真的弱几乎周期点.1993年，Coven等［3］定义了熵极小系统概念，如果有非空不变闭子集Y⊆X，使得ent（f|Y）＝ent（f），则Y＝X，即熵极小系统没有真子系统和原系统的熵一致，熵极小系统是拓扑传递的，以及线段上拓扑传递分段单调的连续映射是熵极小的.王肖义等［4］定义了混沌极小系统概念，如果它本身在Li－Yorke意义下是混沌的，并且所有真子系统都不是Li－Yorke混沌的，讨论其部分动力性状.本文给出了真弱几乎周期点极小系统这一新概念，即f是有真的弱几乎周期点，若Y是X的关于f不变的非空闭子集，且f|Y具有真的弱几乎周期点，则Y＝X.

1 基本概念和记号

设（X，f）是一个紧致系统，Z＋为正整数集.假设U，V⊆X是两个非空开集，x∈X.记N（U，V）＝｛n∈Z＋|U∩f－n（V）≠Ø｝和N（x，U）＝｛n∈Z＋|fn（x）∈U｝.

设S⊆Z＋，令η（S）＝，这里＃（·）表示集合的基数.若η（S）＞0，则称S有正上密度（PUD）.

设x∈X，x在f的作用下生成的轨道｛x，f（x），f2（x），…，fn（x），…｝记作orb（x），易见是对f不变的闭子集.

A⊂Z＋称为相对稠密的，若存在N∈Z＋使得对于任意n∈Z＋，［n，n＋N］∩A≠Ø.

如果对任意的两个非空开集U，V，有N（U，V）≠Ø，则称f是拓扑传递的；如果对任意的两个非空开集U，V，N（U，V）具有正上密度，则称f是拓扑遍历的；如果对任意的两个非空开集U，V，N（U，V）是相对稠密的，则称f是拓扑强遍历的.

M称为极小的，如果M是X的非空不变闭子集，且不存在M的真子集满足上述性质.假如M⊆X是极小的，x∈M，则称x是f的一个极小点，f所有的极小点的集合记为A（f）.

点x∈X称为f的一个弱几乎周期点，对任意的ε＞0，存在整数Nε＞0，使得基数

上式中：V（x，ε）＝｛y∈X|d（x，y）＜ε｝是x的半径为ε的球形邻域；f的所有弱几乎周期点的集合记为W（f）.

给定一个紧致系统（X，f），如果W（f）－A（f）≠Ø，则称该系统含有真的弱几乎周期点［1］.

用M（X）表示可测空间（X，β（X））上的全体概率测度的集合，这里β（X）表示由X上的开集所生成的Borel－σ代数，它是一个可度量紧致有仿射结构的凸空间，其上拓扑称为ω＊拓扑.m∈M（X）称作f的不变测度，如果m（f－1（A））＝m（A）对于任意的A∈β（X）成立.f的全体不变测度的集合记为M（X，f）.设m∈M（X，f），用supp（m）表示m的全体支撑点的集合，即

（X，f）称为E－系统，若f是拓扑传递的，且存在m∈M（X，f），使得supp（m）＝X.如果存在X中的非空不变闭子集E，使得m（E）＝1对于任意的m∈M（X）成立，且E无真子集满足上述条件，则称E是f相对X的测度中心，将f的测度中心记为M（f）［5－6］.

设V⊆X，δ＞0，记Sf（V，δ）＝｛n∈Z＋|d（fn（x），fn（y））＞δ，x，y∈V｝.f是初值敏感依赖的，如果存在δ＞0，对于X中的任意非空开集V，集合Sf（V，δ）是非空的.此时，δ称为f或（X，f）的敏感依赖系数.f是遍历敏感的，如果存在δ＞0，对于X中的任意非空开集V，集合Sf（V，δ）有正上密度.f称为完全遍历敏感的，如果对任意的n＞0，fn是遍历敏感的［7］.

f是Takens－Ruelle混沌的，如果f是拓扑传递的和初值敏感的.设（X，f）和（Y，g）都是紧致系统，如果存在同胚映射h∶X→Y使得hf＝gh，则称f和g拓扑共轭，记作f～g.

定义1（X，f）称为真弱几乎周期点极小的，是指f具有真的弱几乎周期点，如果Y是f的非空不变闭子集，f|Y具有真的弱几乎周期点，则Y＝X.显然，每一个真弱几乎周期点极小系统都不是极小的.

注1熵极小系统和混沌极小系统均可以不是真弱几乎周期点极小系统.

2 主要结论和证明

引理1设（X，f）是一个紧致系统，X中没有孤立点，Λ⊂X是对f不变的闭子集，则有

1）W（f）∩Λ＝W（f|Λ）；

2）A（f）∩Λ＝A（f|Λ）.

证明 对于任意的x∈W（f）∩Λ，由弱几乎周期点定义知：对任意的ε＞0，存在Nε＞0使得基数

由于x∈Λ，且Λ关于f不变，所以对于任意的n∈Z＋，有fn（x）∈Λ.如果fr（x）∈V（x，ε），显然有fr（x）∈V（x，ε）∩Λ，从而有

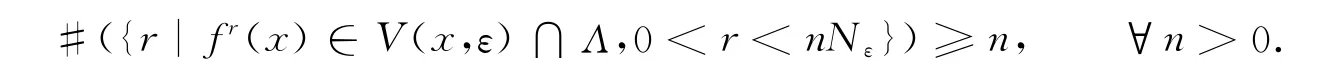
由弱几乎周期点的定义知：x∈W（f|Λ），故W（f）∩Λ⊂W（f|Λ）.

对于任意的x∈W（f|Λ），显然x∈Λ，又由弱几乎周期点定义知：对任意ε＞0，存在Nε＞0，有

x∈W（f），则x∈W（f）∩Λ，故W（f|Λ）⊂W（f）∩Λ.综上可知：W（f）∩Λ＝W（f|Λ）.

对于任意的x∈A（f）∩Λ，由几乎周期点定义知：对任意ε＞0，存在整数N＞0，对任意整数q＞0，存在整数r，q＜r≤q＋N，有fr（x）∈V（x，ε）.又Λ⊂X是对f不变的闭子集，且x∈Λ，有fr（x）∈Λ，则fr（x）∈V（x，ε）∩Λ，即（f|Λ）r（x）∈V（x，ε），则x∈A（f|Λ）.

故A（f）∩Λ⊂A（f|Λ）.

对于任意的x∈A（f|Λ），显然x∈Λ，且必存在一个非空的不变子集M⊂Λ，使得f|M对于Λ是极小的，显然f|M对于X是极小的，并且有x∈A（f），则x∈A（f）∩Λ.故A（f）∩Λ⊃A（f|Λ）.综上可知：A（f）∩Λ＝A（f|Λ）.

定理1设（X，f）是一个真弱几乎周期点极小系统，则f是拓扑传递的.

证明 由于f具有真的弱几乎周期点，则存在x∈X使得x∈W（f）－A（f）.由轨道定义知：是（X，f）的一个子系统，且.由引理1中1）知：由引理1中2）知：从而即x也是子系统的一个真的弱几乎周期点.

由于（X，f）是真弱几乎周期点极小系统，根据定义知：orb（x）＝X.由于X中无孤立点，所以f是拓扑传递的.

注2若f是拓扑传递的，则（X，f）不一定是真弱几乎周期点极小系统.

定理2设（X，f）是一个真弱几乎周期点极小系统，则f具有满测度中心，即M（f）＝X.

证明 由定理条件知：W（f）－A（f）≠Ø，又（M（f），f|M（f））是（X，f）的一个子系统.设x∈W（f）－A（f），即x∈W（f）但x∉A（f）.由于，则x∈M（f）.由引理1中（1）知：x∈W（f|M（f）），又由引理1中（2）知：x∉A（f|M（f））.则x∈W（f|M（f））－A（f|M（f）），即x是子系统（M（f），f|M（f））的一个真的弱几乎周期点.又（X，f）是真弱几乎周期点极小系统，根据定义知：M（f）＝X.

引理2［8］设（X，f）是紧致系统，若f是拓扑传递的，且M（f）＝X，则（X，f）是一个E－系统，且f是强遍历的.

定理3设（X，f）是一个真弱几乎周期点极小系统，则f是强遍历的.

证明 由定理1，2知：f是拓扑传递的，且M（f）＝X.则由引理2知：f是强遍历的.

引理3［6］非极小的E－系统是初值敏感的.

引理4设（X，f）是一个真弱几乎周期点极小系统，则f是初值敏感的.

证明 由定义1知：f不是极小的.定理1，2知：f是拓扑传递的，且M（f）＝X，则由引理2知：（X，f）是一个E－系统.由引理3知：f是初值敏感的.

定理4设（X，f）是一个真弱几乎周期点极小系统，则f是Takens－Ruelle混沌的.

证明 由定理1知：f是拓扑传递的，由引理4知：f是初值敏感的.根据Takens－Ruelle混沌的定义可得，f是Takens－Ruelle混沌的.

引理5［7］设（X，f）是一个紧致系统，若f是初值敏感的，且f×f的弱几乎周期点在X×X中稠密，则对于任意n＞0，fn是遍历敏感的，即f是完全遍历敏感的.

引理6设（X，f），（Y，g）是2个紧致系统，则M（f）×M（g）＝M（f×g）.特别地，M（f）×M（f）＝M（f×f）.

证明 设（x，y）∈M（f）×M（g），对于（x，y）任意邻域U，存在x的一个邻域U1⊆X和y的一个邻域U2⊆Y，使得U1×U2⊆U.由于x∈M（f），y∈M（g），则x，y分别是f和g的支撑点，于是存在μ1∈M（X），μ2∈M（Y），使得μ1（U1）＞0，μ2（U2）＞0.

令m（U1×U2）＝μ1（U1）×μ2（U2），则m可以延拓到M（X）上而成为一个不变测度，记延拓后的测度为m，则m∈M（X×Y），且m（U）≥m（U1×U2）＞0，所以（x，y）是f×g的一个支撑点，于是（x，y）∈M（f×g）.

令V1＝V（x，ε1），V2＝V（y，ε2），由于（x，y）∈M（f×g），根据弱几乎周期点的定义知：存在N＞0，使得对于任意n≥0，

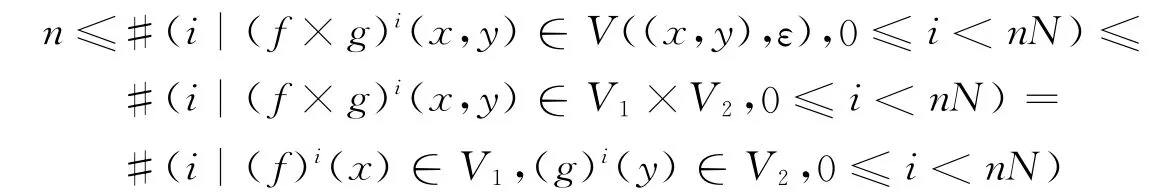
则＃（i|（f）i（x）∈V1，0≤i＜nN）≥n，且＃（i|（g）i（x）∈V2，0≤i＜nN）≥n.

故x∈M（f），y∈W（g）.则证明得W（f×g）⊆W（f）×W（g）.从而

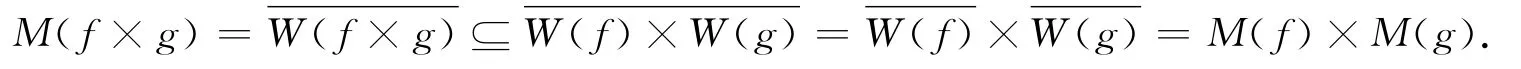
定理5设（X，f）是一个真弱几乎周期点极小系统，则f是完全遍历敏感.

证明 由引理4知：f是初值敏感的.由定理2知：f具有满测度中心，W（f）＝X.根据引理6知：W（f×f）＝M（f×f），即f×f的弱几乎周期点在X×X中稠密.由引理5可得：f是完全遍历敏感的.

引理7［2］假设（X，f），（Y，g）是两个紧致系统，f～g，且h∶X→Y是从f到g的拓扑共轭，那么h（W（f））＝W（g）.

定理6设f～g，且h∶X→Y是从f到g的拓扑共轭，若（X，f）是真弱几乎周期点极小系统，则（Y，g）也是真弱几乎周期点极小系统.

证明 假设（Y，g）不是真弱几乎周期点极小系统，即存在（Y，g）的真子系统（U，g|U）中含有真弱几乎周期点，即W（g|U）－A（g|U）≠Ø，显然（h－1（U），f|h－1（U））是（X，f）的真子系统，且f|h－1（U）与g|U共轭.由引理7知：hW（f|h－1（U））－hA（f|h－1（U））≠Ø，则W（f|h－1（U））－A（f|h－1（U））≠Ø，则（X，f）的真子系统（h－1（U），f|h－1（U））含弱几乎周期点，与已知矛盾，假设不成立.

故（Y，g）是真弱几乎周期点极小系统.

注3此定理说明两个紧致系统拓扑共轭，若其中一个为真弱几乎周期点极小系统，另一个系统也为真弱几乎周期点极小系统.若h只是从X到Y的拓扑半共轭，上述结论可能不成立.

［1］周作领.弱几乎周期点和测度中心［J］.中国科学：A 辑，1992，22（6）：572－581.

［2］周作领，何伟弘.轨道结构的层次与拓扑半共轭［J］.中国科学：A 辑，1995，25（5）：457－464.

［3］COVEN E，SMITAL J.Entropy－minimality［J］.Acta Math Univ Comenianae，1993，62（1）：117－121.

［4］王肖义，黄煜.不含混沌真子系统的Li－Yorke混沌［J］.数学学报，2012，55（4）：749－756.

［5］周作领，尹建东，许绍元.拓扑动力系统：从拓扑方法到遍历理论方法［M］.北京：科学出版社，2011：117－120.

［6］叶向东，黄文，邵松.拓扑动力系统概论［M］.北京：科学出版社，2008：29－60.

［7］LI Ri－song.A note on stronger forms of sensitivity for dynamical systems［J］.Chaos，Solitons and Fractals，2012，45：753－758.

［8］YIN Jian－dong，ZHOU Zuo－ling.A characterization of topologically transitive attributes for a class of dynamical system［J］.Chinese Annals of Mathematics，2012，33（3）：419－428.